
|
BMe Research Grant |

|
Csonka Pál Doctoral School
Department of Mechanics, Materials and Structures
Dr. István Sajtos
Application of Geometric Method for the Research of Buckling of Spherical Shells
Introducing the research area
The research focuses on the buckling of the total spherical shell loaded with concentrated force or distributed load. There are many questions about the shell buckling which have not been answered as yet. One can observe that the theoretical and experimental results about the buckling load differ. Also, there can be many different kinds of buckling shape in some cases for one given shell. It could be experienced in several cases that the sphere remains in the buckled state even after the load is removed. We try to find the explanations for these phenomena and answer these questions.
Brief introduction of the research place
The Department of Mechanics, Materials and Structures is engaged in a big variety of problems in the field of structural design. The research topics are related to steel, timber, reinforced concrete, masonry and composite structures. Morphological and topological problems, stability of shell structures are also a part of their research activity, both from theoretical, and from practical point of view and there have been 17 successful PhD defenses.
History and context of the research
Relatively thin surface structures that have curved middle surface are called shells. One can find them at many places in engineering practice, e.g. domes (Fig. 1.), silos, containers, pressure vessels, different vehicles (Fig. 2.), micro switches. Similar constitutions can be found in nature as well, e.g. stem cells (Fig. 3.), unicellular organisms, bacteria (Fig. 4.), organs (heart, circulatory system). It is also important to keep in mind that engineering structures can lose their stability, which means a change in the load-bearing capacity of the structure due to the change of the geometry describing it. The loss of stability of shells is called buckling. Finding the buckling load of shells is not a simple task and has not been completely worked out as yet. The difference between theoretical and experimental results cannot be merely attributed to shape imperfections in experiments, but also due to the insufficiencies in theoretical models.

Fig. 1.

Fig. 2.
Fig. 3.
Fig. 4.
In the 1950s, A. V. Pogorelov worked out the so-called geometric
shell buckling theory. Although known to scientists since its publication, its applicability was severely constrained by the fact that the assumption of
the buckled shape has only been based on experiments. During the last 10 years
scientists – mainly physicians – laid the determination of the buckled shape on
mathematical bases, but the load-deflection diagram of the shell was examined
only qualitatively. For engineers, quantitative determination of
buckling load may also be essential.
Aim of the research
The main purpose of the research is to determine the load-deflection diagram of spherical shells using Pogorelov's geometric shell buckling theory. The determination of the load-deflection diagram is important because the notable points on the curve correspond to the buckling load of the shell. The load-deflection diagram that describes the behaviour of real (imperfect) shells (Fig. 5.) has typically one maximum and one minimum, and the corresponding load values are called upper and lower critical loads. The maximum on the load-deflection diagram of the theoretical (perfect) shell is called linear critical load, but only a fraction of this value is reached in real shells.

Fig. 5.
When determining the buckling load one should consider that additionally to the size, the character of the buckling shape may change during the
buckling of a shell. In the case of spherical shells, the buckling shape can be circular i.e. rotationally symmetric, or polygonal with a discrete symmetry of revolution. The cycle number of
the discrete symmetry of revolution (the number of sides of the polygon) can
change as the load increases. The buckling shape can be determined from shell dimensions, elasticity data, support construction of the shell and
the character and intensity of the load. Therefore, it is important for the research to determine the buckling shape of a shell for given conditions.
There are various equilibrium paths or surfaces in the load-deflection diagram
that correspond to these shapes. Their intersections represent the transitions between
these shapes.
Based on these investigations, we can probably give the
measurement and curvature values or load types that allow a negative buckling load of
the shell. This would verify the experience – that has no
unambiguous explanation as yet – that a shell made of elastic material does
not always return to its original state after the load is removed. To verify this experience is among the most important goals of this research work.
Methods
During the research, more precise models had to be considered.
Initially, our research originated from Pogorelov's method developed in the 1950's, the so-called
geometric shell buckling theory, which is still used by researchers. It searches the equilibrium states of the shell using the energy method supposing a buckling shape of the spherical shell surface – approximately – to be
close to the isometrically transformed shape of the original spherical surface
[3].
In the physical sense, the isometrically transformed shape of a surface is the form that can be reached by inextensional deformations. In other words, the shape of a
surface is changed without applying any stretching, compressing, cutting or distorting, and exclusively through bending, like folding a sheet of paper. It is generally true
for shells that – because of their thinness – their rigidity against bending is
much lower then against stretching. So it seems a reasonable assumption that shell deformations during buckling are nearly
inextensional.
At the early stage of the research we managed to construct the
load-deflection diagram of the total sphere for a few simple cases introducing some
modifications into Pogorelov's method [1], [2]. The buckling shape was an
isometrically transformed form of the sphere that can be created through
mirror-reflecting a part of the original spherical surface (Fig. 6.). It was
a rotationally symmetric shape, with a circle as the edge of the buckled region.

Fig. 6.
Next, the buckled shapes were considered as ones that cannot
be created by inextensional deformations. We could observe these shapes in our experiments as well,
and generally exhibited discrete symmetry of revolution, i.e. the buckling edges form a polygon (Fig. 7.). A common example for this shape is a damaged ping-pong ball. The question to be answered was what the shape of the buckled shell would look like. Initially, for simplicity, we neglected the
stretching energy even where it obviously did appear, and approximated
the buckling shape with a pyramid of planar sides. It turned out that the
curves belonging to different polygons did not coincide in the
load-deflection diagram, but laid relatively close to each other, so a more precise
model was required.

Fig. 7.
This lead us to take stretching energy into consideration to get more accurate results. Simultaneously with this, we extended the number of variables describing the buckled shape from one to three [4]. In the present
model, these variables are as follows: depth of
the centre of the buckled region, radius of the so-called inner circle
(i.e. the one made with mirror-reflection and located in the middle of the
buckled zone), and number of sides of the buckling polygon (Fig. 8.). This
number of variables substantiates the use of a proper numerical method to find the
equilibrium states. On the load-deflection diagram we can see equilibrium
surfaces, not curves (Fig. 9.).

Fig. 8.
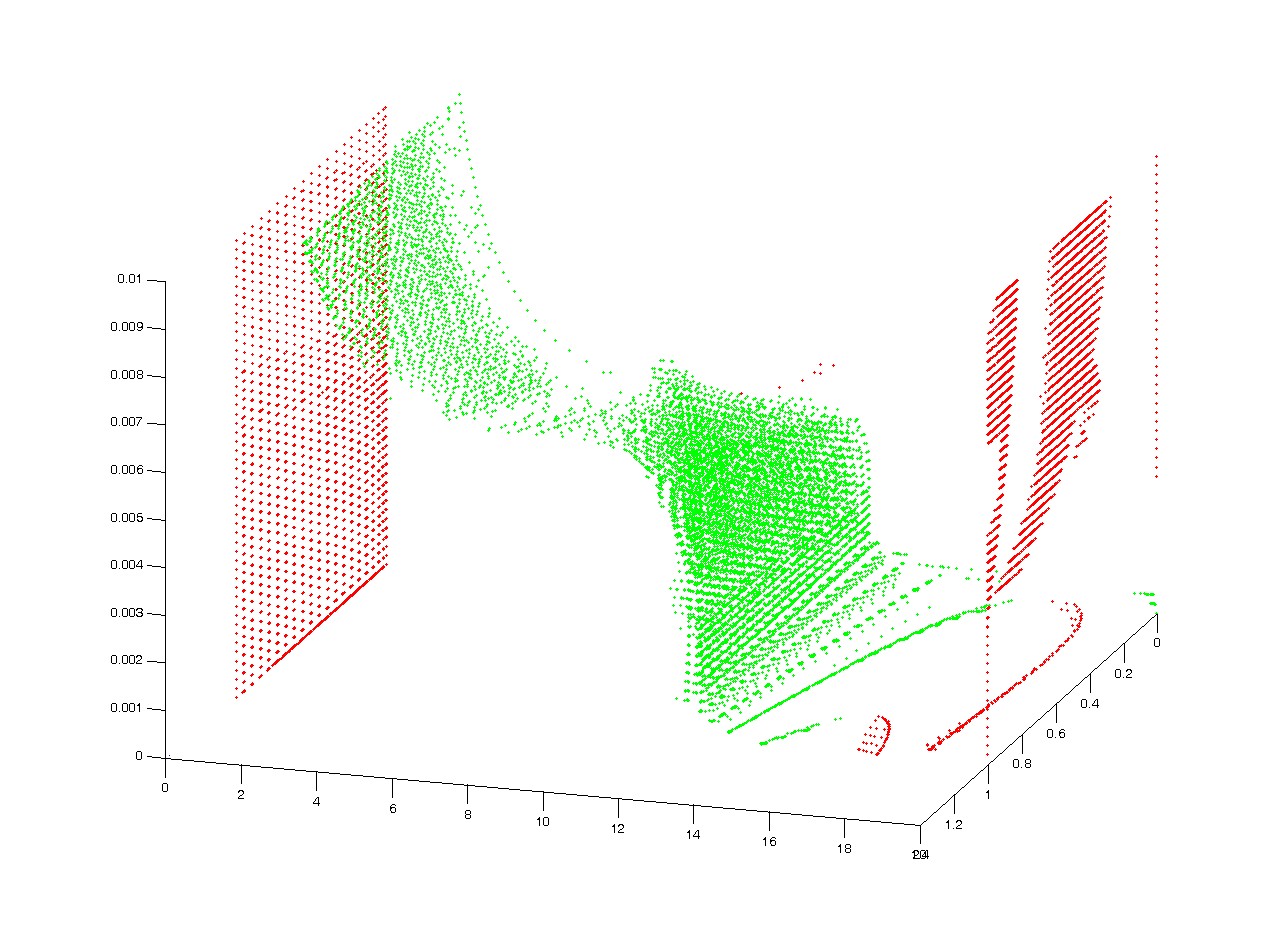
Fig. 9.
Results
At the initial stage of the research, we supposed a rotationally symmetric buckled shape, so we selected the buckled form as an isometrically transformed form of the original shell surface. The results that we got with this assumption noticeably differ from Pogorelov's results for parallel, evenly distributed load. This deviation can be attributed to Pogorelov's approximation of the buckled shape with an osculating paraboloid, although this shape – as one created with the inversion of a part of the sphere (at least by our assumption) – should also be spherical. An important result is that the spherical shell has an increasing load-deflection curve for concentrated forces (Fig. 10.a), on the other hand, it has a minimum for parallel or radial distributed loads (Fig. 10.b).
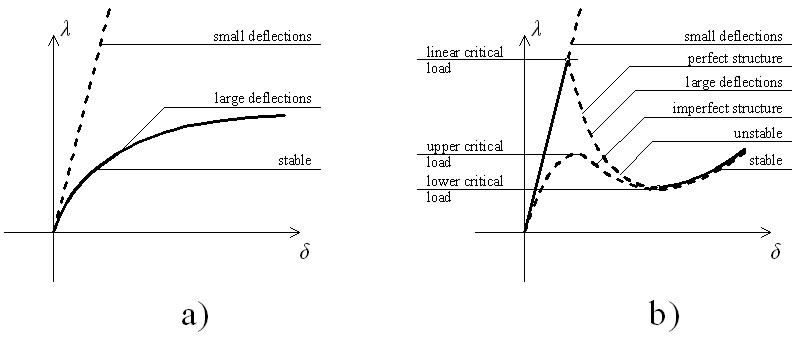
Fig. 10.
In the research work that followed, the forms we used as buckling shapes could not be
created with inextensional deformations of the original surface. In our initial
investigations we neglected stretching energy. The buckling shapes belonging
to different polygons laid close to each other (Fig. 11.), see
[1] for details. This suggested that a more precise model was needed.
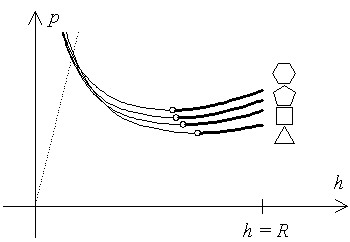
Fig. 11.
Our next model described the buckled shape with multiple variables:
depth of the centre of the buckled region, radius of the circle located in the middle of the buckled zone, and number of sides of the buckling
polygon. The equilibrium states on the load-deflection diagram were not curves,
but equilibrium surfaces and we used a numerical method, based on the
so-called gradient method for finding them. Note that the equations in our newest model
will contain stretching energy as well.
Expected impact and further research
Further research includes investigation of possible ways of application of our results for solving problems in engineering and biology. We also aim at determining how the buckling shape and load depends on geometrical, material
properties and load type.
The knowledge of buckling load belonging to
the buckling shapes found in experiments can make the design of structures "made
of sphere" more accurate. The generalization of the results obtained for sphere enables improving the accuracy of the bucking investigation of elliptic surfaces with arbitrary curvatures.
Publications, references, links
[1] Vető, D. – Sajtos, I.: Application of Geometric Method to Determine the Buckling Load of Spherical Shells. Pollack Perodica, 4 (2), pp. 123–134. (2009)
[2] Vető, D. – Sajtos, I.: Application of Geometric Method to Determine the Buckling Load of Spherical Shells. ed.: Lehoczky, L.: XXIII. microCAD International Scientific Conference, University of Miskolc, 19–20. March, 2009, Miskolc, Hungary, Innovation and Technology Transfer Centre, Miskolc, pp. 61–66. (2009)
[3] Vető, D. – Sajtos, I.: Application of Geometric Method to Determine the Buckling Load of Spherical Shells. ed.: Iványi, M.: Pollack PhD, Fourth International PhD, DLA Symposium, University of Pécs, Pollack Mihály Faculty of Engineering, 20–21. October, 2008, Pécs, Hungary, Rotari Press, Komló, p. 61. (2008)
[4] Vető, D. – Sajtos, I.: Investigation of Buckling of Spherical Shells.
FUDoM 09, Finno-Ugric International Conference of Mechanics, 23–29.
August, 2009, Ráckeve, Hungary, pp. 31–32.
(2009)
