 |
BMe Research Grant |

|
BME Pál Vásárhelyi Doctoral School in Civil Engineering and Earth Sciences
BME Department of Structural Engineering
Supervisor: Dr. István Bódi
Experimental and numerical investigation of reinforced and plain masonry walls
Introducing the research area
Brick has been used since the earliest times. The
ancient Egyptians, Romans and Greeks built lots of monumental structures from
masonry such as the pyramid of Cheops in Egypt, the Greet Wall of China, the
Pharos of Alexandria, etc. However, the knowledge about the behaviour of masonry
is almost the least complete today of the building materials.
The application of masonry structures in Hungary is
not so varied than it is overseas. In Hungary, reinforced concrete frames are
favoured in building-trade nowadays. In that case, masonry is merely used as
an infill wall. In the USA and in England, load bearing masonry walls are built
for 4-10 storey buildings without reinforced concrete frames. According to the
experience of the last decades, reinforced masonry is cheaper, quicker and more
eco-friendly building method than reinforced concrete wall systems.
Masonry walls have enough compressive resistance to
transmit vertical forces without failure. However, their load bearing capacity
against horizontal loads (wind, earthquake) and deformation capacity is
low. With the introduction of the new European earthquake standard the
design requirements of Eurocode 8 can be fulfilled with difficulty for
middletall masonry buildings. If reinforcing bars are placed in mortar joints or
pockets, the deformation, load bearing capacity and resistance against
extraordinary loads (impacts, earthquakes, vibration) changes beneficially. [1,
2, 3, 4]
Brief introduction of the research place
The Department
of Structural Engineering of Faculty of Civil Engineering deals with the
structural design and analysis of superstructures, buildings and bridges. Our
department disposes the biggest laboratory of the faculty that is appropriate
for experimental investigation of structures and provides place for experiments
necessary for the research, teaching and design. Our subjects base
the professional knowledge of future structural engineers.
History and context of the research
The international literature describes reinforced masonry systems that place the vertical reinforcement in the middle of special masonry units or in which the bricks are layered in special order to form a reinforced concrete column at the center. In both cases, the pockets or holes are filled with concrete. The advantages of these walls were investigated by numerous researchers. It would be too expensive to analyze every possible loading cases, masonry units and brick bonding possibility. Applying numerical models, those virtual experiments are also executable that do not dispose of technical and financial background for execution.
Prerequisite of the modelling is the knowledge of the mechanical characteristics of constituents. Due to the big variety of mortar, masonry units and their manufacturers, differences can not only be observed in the mechanical properties of materials but there is a spread in the literature data available for them. In Hungary, manufacturers do not have information on all features, and standard investigation methods are only available for the investigation of the mechanical features of masonry.
For these reasons, a lot of researchers deal with material and modelling problems in the field of load bearing masonry. The most widespread numerical modelling methods in this research area are finite and discrete element methods. The latter one was chosen for the analysis because no three dimensional discrete element model applied for masonry walls and backed with experimental research has been published as yet.
The research goal, open questions
The dissertation is the first part of a year-long research project conducted in cooperation with the biggest Hungarian brick manufacturer and
an international engineering consulting and
software development firm. The final goal of the research is to construct a building method that ensures bigger deformation capacity for masonry walls adjusted to the Hungarian brick types, building systems and tradition, which enables application of masonry systems to middle-high buildings. In order to make the design easier the following needs to be determined: where to place the reinforcement and what brick bonding technology should be used to attain the most economical implementation. This will enable us making recommendations for brick manufacturers to consider upon compiling their selection of masonry units.
The primary aim of the research is the determination of the mechanical parameters of brick and mortar missing from the literature. Based on these parameters, a plain masonry modelling system can be developed and the behavior of the model can be confirmed through experiments. One of the aims was developing a new brick bonding method for reinforced masonry, determining its advantages and disadvantages compared to traditional masonry walls and confirming its enhanced resistance against horizontal loads. Based on experiments, models can be developed that prove that buildings of more than 2-3 storeys can be built from reinforced masonry while meeting the design requirements.
Methodology
The failure modes of plain masonry walls subjected to different loading directions and loading types were collected, grouped and typed. In order to determine the failure modes of reinforced masonry (how reinforcement affects the crack pattern, deformation and load bearing capacity) experimental investigations were carried out. It was stated that the failure occurs mostly at the brick-mortar joint in the case of the plain and reinforced masonry, as well.
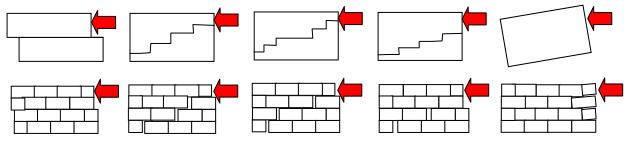
Figure 1: Failure modes in case of walls subjected to horizontal loads
Three methods are frequent for modelling masonry: the first one where both the mortar and the masonry unit are modelled separately (Figure 2 a), a second where the unit is simulated (b) and a third one where the constituents are not shown separately, only one homogenous material symbolizes the behaviour of the wall (c).
Figure 2: The modelling methods of masonry: a) micromodel, b) simplified micromodel, c) macromodel (Lourenco, 1996)
As failures in plain and reinforced masonry occur at the surface of the unit-mortar joint and not in the mortar itself, if modelling conditions allow, a simplified micromodel can be created for both cases. With the help of a simple 2D discrete element model it was confirmed that all possible failure modes of reinforced masonry can be modelled by adequately choosing the parameters
[15].
We have set three conditions for a proper 3D masonry wall model:
1. The model has to show the same joint behavior as described in the literature in details.
2. The model has to provide the same crack pattern as in the experiments using the material characteristics determined according to the experiments with brick and mortar specimens.
3. Any point of the wall should be displaced to the same extent under the same loading both in the model and in the experimental setup.
The key issue of the discrete element modelling is the determination of the mechanical material properties and other parameters that can not be determined by experiments. Because of the antinomic and deficient nature of the information on these parameters in literature, own experimental measurements were necessary.
In the Structural Laboratory of the Department of Structural Engineering and of
the Department of Construction Materials and
Engineering Geology destructive and non-destructive measurements were carried out in order to determine the size and loading direction dependent material parameters. Additionally, experimental investigations were carried out on plain, horizontally, vertically and in both direction reinforced masonry walls subjected to horizontal loads in order to determine their behavior. (Click here
to see a movie of a failure of an experimental wall)




Figure 3: Parts of the experiments carried out
Results
1. A special, new type of brick laying method was worked out that enables placing reinforcing bars in the middle of the wall and in the mortar joints while fulfilling the overlapping requirements of brick bonding. This method provides smaller pockets for placing reinforcement than those that can be found in the literature. This system is unique among reinforced masonry types, because the same mortar can be used for filling the vertical pockets and bed joints of masonry. [5, 7]
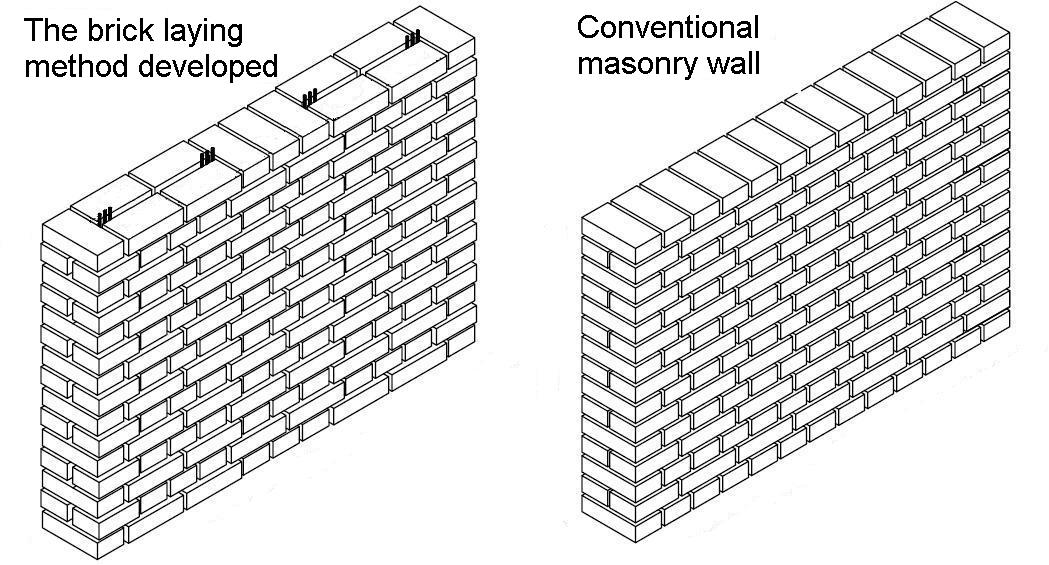
2. To prove the beneficial behavior of the new system, a series of experiments were carried out on various masonry walls using two types of mortars. It was proved that in the new system the first cracks appear only after twice as large displacements and at 20% higher load levels than in conventional masonry walls. Before the final failure, the new walls are capable of 10 times higher deformation then conventional masonry walls. This system is beneficial in blast or earthquake hazarded areas, next to temporary vacant building sites or for partition walls or for walls that are loaded with earth pressure. [8, 9]
3. Based on the experiments, characteristic failure mechanisms were analyzed and the influencing parameters were determined. In order to simplify the design work of engineers a design method was developed to analyze the behavior of these new type of walls subjected to shear. [10]
4. In close cooperation with Wienerberger company, mechanical properties of the brick unknown for the manufacturer but necessary for the design have been determined. Experimental investigations were carried out on more than 100 brick specimens and the reasons for contradictions in literature were clarified. It was stated that bricks show different behavior in each loading directions. It was determined how the material features depend on the following parameters: the roughness of surface, the height, length, width and shape of specimen, the type of sampling (bored or cut), and loading direction. The mechanical properties of one Hungarian mortar that is important from the design point of view were measured on more than 50 specimens. [13]



5. A 3D discrete element model was built to simulate the behavior of the brick-mortar joint based on the parameters determined in the experiments. With the application of the results, a wall model was created for conventional solid brick masonry that governs the same crack pattern (Figure 6 a), deformation and load bearing capacity as that of the experiment. The developed model is appropriate for the simulation of the experiments carried out and it is possible to model the real wall subjected to the same load with adequate choice of parameters. The sizes, layout and the properties of the units as well as the loading direction of the wall are variable arbitrarily in the model. Figure 6 b shows the failure of a fictitious wall in the case of an impact of high velocity on the middle brick in the wall. [14] (Click here to see a movie of a failure of the wall.)
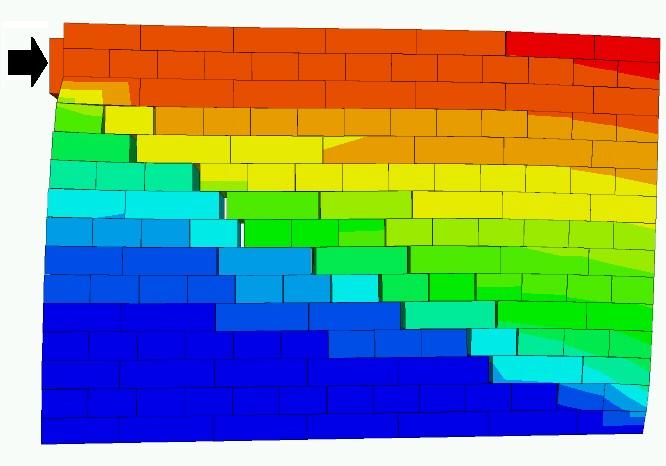
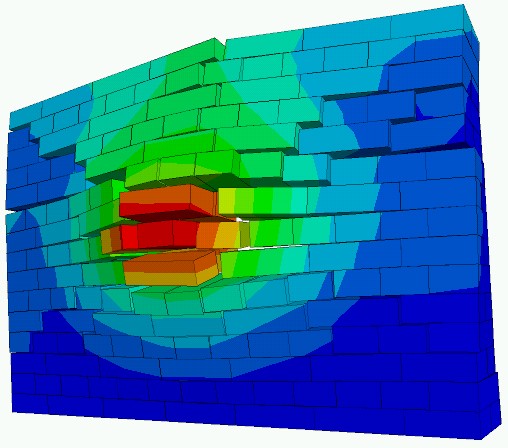
6. It was shown that the discrete element model of the plain masonry allows the simulation of the failure modes and behavior of the reinforced masonry with adequately choosing the parameters. Further research aim is to analyze the behavior of other masonry unit types and reinforced masonry systems.
Expected impact and further research
After further analysis of the developed building system, a new masonry building method can be implemented that meets the requirements to earthquakes even in the case of higher buildings. Comparing the numerous experimental investigation of masonry walls subjected to shear with the numerical model helped suggesting model parameters for plain and reinforced masonry. This work can be the base for numerical analysis.
The results of the experiments of more than 100 brick and 50 mortar specimens provide mechanical material parameters for forthcoming researches and projects. In the future, a larger scale model of buildings is planned to be developed to prove applicability of the new masonry system as masonry shear wall in 3-5 storey buildings.
Publications, references, links
Related publications:
[1] Fódi, A.
Conclusion from seismic tests on realized , conventional buildings (in Hungarian). Doctoral researches at the Faculty of Civil engineering of BME (Ed.:
Zsolt Barna), Budapest, Nov. 14, 2007., pp. 93–102.
[2] Fódi, A., Bódi, I.
Reinforced masonry structures – European history – Hungarian present practice.
Proceedings of the 6th International Conference Analytical Models and New
Concepts in Concrete and Masonry Structures, Łodź, Poland,
09-11 June, 2008, pp.1–8. (open
article)
[3] Fódi, A., Bódi, I. Status
of reinforced masonry in Hungary. Proceedings of the 4th Central European
Congress on Concrete Engineering: Concrete Engineering in Urban Development
(Ed.: Jure Radic, Jelena Bleiziffer), Opatija, Croatia,
02-03 October, 2008., pp. 517–522.
[4] Fódi, A. Conclusions from seismic tests on realized, mid-height reinforced concrete framed buildings (in Hungarian). Magyar Építőipar, Vol. 59:3, 2009/3., pp. 96–100.
[5] Fódi, A., Bódi, I.
Experimental and numerical analysis of plain and reinforced masonry walls built of solid brick under shear in its own plane (in Hungarian). ÉPKO2009, XIII.
Nemzetközi Építéstudományi Konferencia, Erdélyi Magyar Műszaki Tudományos
Társaság (Ed.: Köllő Gábor), Csíksomlyó, 11-14 June, 2009., pp.
144–151.
[6] Fódi, A. Application of masonry structures (in Hungarian). Study prepared for Wienerberger Zrt, 2009
[7] Fódi, A., Bódi, I. Shear
capacity and crack pattern of reinforced and plain masonry walls. 8th fib PhD
Symposium in Kgs. Lyngby, Denmark, 20-23 June, 2010., pp. 69–74. (open
article)
[8] Fódi, A., Bódi, I. The
effect of horizontal and vertical reinforcement on the shear capacity of masonry
walls. SEMC 2010, The 4th International Conference on Structural Engineering,
Mechanics and Computation, Cape Town, South Africa, 6-8 September, 2010., pp.
997–1000.
[9] Fódi, A., Bódi, I.
Experimental investigation of solid masonry walls reinforced in different
directions. 8IMC 8th International Masonry Conference 2010 in Dresden,
Germany, 4-7 June, 2010., pp. 843–852. (open
article)
[10] Fódi, A., Bódi, I.
Comparison of shear behaviour of masonry walls with and without reinforcement.
POLLACK PERIODICA, 2010 Vol. 5. No. 3. pp. 71–82. (open
article)
[11] Klouda, J. K., Fódi, A., Kubica, J., Popescu, R. &G., Bosiljkov, V. Preparation for the Shear Wop at 8IMC on July 4, Region: MEE-Middle-East-Europe. Ed.: V. Bosiljkov, 2010
[12] Fódi, A., Bódi, I. Basics
of reinforced masonry. Journal of CONCRETE STRUCTURES, 2011, Vol. 12 (open
article)
[13] Fódi, A. Effects influencing the compressive strength of a solid, fired clay brick. PERIODICA POLYTECHNICA Civil Engineering, 2011, (under publishing)
[14] Fódi, A., Bódi, I. The behaviour of a simplified micromodel for masonry. HCTAM, 2011, 11th Hungarian Conference on Theoretical and Applied Mechanics, Miskolc, Hungary, 29-3. August, 2011., (under publishing)
[15] Fódi, A. Degradation test of masonry built of small bricks under shear in its own plane (in Hungarian) "Micromechanics of Grainy Materials", homework assignment, 2009 (open
article)
Links
Department of Structural Engineering
The author would like to express her grateful thanks to those person and firms who help and helped accomplish the research project: Wienerberger Ltd, that provided materials and subsidy and Itasca Consultants, S.A.S., the international software developer firm that provided for one year the use of the 3DEC discrete element model program in the frame of the Itasca Education Partnership Program.
References
Abrams, D P. Masonry in the Americas. American Concrete Institute, SP-147, Detroit, Michigan, 1994.Amrhein, J E. Reinforced masonry engineering handbook. Masonry Institute of America, 1973.
Anderson, T L. Fracture mechanics. CRC Press, 1995
Andrejev, Sz A. Design and calculation of masonry structures. É.M. Építőipari könyv- és lapkiadó, Budapest, 1953
Árva, P, Sajtos, I. Determining of the condition of masonry failures with homogenisation. Abstract of the 10th Hungarian Conference for Mechanics (IUTAM), August 27-29, 2007, 3 p.
Bagi, K. The discrete element method. Lecture notes, BME Tartószerkezetek Mechanikája Tanszék Budapest, 2007
Beamish, R. Memoir of the life of Sir Marc Isambard. Brunel, civil engineer, vice-president of the Royal Society, corresponding member of the Institute of France. Longman, Green, Longman and Roberts, London
Bekaert, Murfor – Reinforcement for masonry, Product identification, range of applications, installation details, design principles. Editor: Timperman P., Bekaert, 2005
BEKAERT Specification: Murfor, reinforcement for brick work. AS-05-19, 2009-05-07.
Berto, L, Saetta, A, Scotta, R, Vitaliani, R. An orthotropic damage model for masonry structures. International Journal for Numerical Methods in Engineering, pp. 127–157, 2002
Bojtár, I. Practical approach for fracture mechanics. Lecture notes, Budapest University of Technology, Department of Structural Mechanics, 2007
Chetouane, B, Dubois, F, Vinches, M, Bohatier, C. NSCD Discrete element method for modelling masonry structures. International Journal for Numerical Methods in Engineering, Volume 64 Issue 1, pp. 65 – 94, 2005
Crisafulli, J F. Seismic behaviour of reinforced concrete structures with masonry infills. Doctoral dissertation. University of Canterbury, Christchurch, New Zealand, 1997
Csák, B, Hunyadi, F, Vértes, Gy. The effect of the earthquakes on buildings. Műszaki Könyvkiadó, Budapest, 1981
D’Ayala D F. Numerical modelling of masonry structures reinforced or repaired. Computer Methods in structural masonry –4, pp 161–168, 1998
Dulácska, E. Earthquake hazard, Protection against earthquakes. TT-TS 3, Logod Bt., (in Hungarian) MMK Logod Bt, Budapest, 2000
Dulácska E. The reconstruction and diagnostic of load bearing elements of buildings (in Hungarian). Lecture notes, 2008
Engineering Structures Research Centre, City University London, Low-rise residential construction detailing to resist earthquake. Repair & Strengthening of Brick/Block masonry. http://www.staff.city.ac.uk/earthquakes/Repairstrengthening/ index.php, Editor: Virdi, K. S. and Rashkoff, R. D., 04. July, 2008
Itasca, 3DEC 3 Dimensional Distinct Element Code Version 4.1, Online Manual
Lourenço P B, Rots J G, Blaauwendraar J. Continuum models for masonry: Parameter estimation and validation. Journal of Structural Engineering, June, pp. 642–652, 1998
Lourenço, P J B B. Computational strategies for masonry structures. Delft University Press Doctoral dissertation, Delft University Press, 1996
MI 15011-1988 Technical directive Műszaki irányelv, Épületek megépült teherhordó szerkezeteinek erőtani vizsgálata), Hungarian Standard, Magyar Szabványügyi Hivatal
McKenzie WMC. Design of structural masonry. Palgrave, New York, pp 2, 2001
MSZ 15023-87. Design of load bearing masonry structures. Magyar Szabványügyi Hivatal, 7. December, (in Hungarian), 1987
MSZ EN 1996-1-1:2006, Eurocode 6 – Design of masonry structures, Part 1-1: Common rules for reinforced and unreinforced masonry structures. 41 p. MSZT, Budapest, April 2006
MSZ EN 772-1:2000 Methods of test masonry units Part 1: Determination of the compressive strength (in Hungarian)
Pate K, Noble W. Stress-strain relationship in heavy clay products. in: Mechanical properties of non-metallic brittle materials, Butterworth, London, 1958, pp 210–216 in: Blight GE, Calculated Load bearing brickwork, Technical Publications, 2009, www.claybrick.org.za
Pluijm, Rvd. Non-linear behaviour of masonry under tension. HERON, Vol. 42, No. 1: 25–54, 1997
Pluijm, Rvd. Shear behaviour of bed joints. Proceedings of the 6th North American Masonry Conference, eds. A.A. Hamid and H.G. Harris, Drexel University, Philadelphia, Pennsylvania, USA:125–136, 1993
Reinhardt, H W. Brickwork. Lecture notes, Universität Stuttgart, Institut für Werkstoffe im Bauwesen, 1989
Rózsa, M. Rules for design of stone-, brick-, reinforced masonry and concrete structures. Felsőoktatási Jegyzetellátó Vállalat, Budapest, 1953
Sajtos, I. The Eurocode 6: Design principles and examples. in: Balázs, L. Gy.: Eurocode 6: Masonry Structures, Építésügyi Minőségellenőrző Közhasznú Társaság, Budapest, pp. 47–84, 2001
Sajtos, I. Reinforced masonry structures – architectural and structural advantages. Építőmester, January-February, pp. 24–25, 2006
Sajtos, I. Reinforced masonry structures. Építéstechnika, pp. 40, 2006
Sajtos, I. Bed joint reinforced masonry structures. Építőmester, May-June, pp. 36–37, 2006
Sajtos, I. Materials of masonry. Ed: S. Fernezely, T. Matuscsák: Load bearing elements of structures, Actual constructional solutions for engineers, Chapter 6.4. Verlag Dashöfer Szakkiadó Kft és T. Bt, Budapest, 2004
Schneider, R R, Dickey, L W. “Reinforced masonry design. Third Edition, Prentice hall, Englewood Cliffs, New Jersey, 1994
Sieh-Beygi, B, Pietruszczak S. Numerical analysis of structural masonry mesoscale approach. Computers and Structures 86: 1958–1973, 2008
Subasic, C A, Borchelt J G. Clay and shale brick material properties – a statistical report. Proceedings of the 6th north American masonry conference, The masonry society, Boulder, CO, 1993, 12 pp., in: Technical Notes 3A – Brick Masonry Material Properties, Technical notes on brick construction, 1992, www.gobrick.com
Zucchini, A, Lourenço P B. A micromechanical model for the homogenisation of masonry. International Journal of Solids and Structures, pp. 3233–3255, 2002
Wienerberger Ltd. Application and design (in Hungarian), Budapest, 2009
