 |
BMe Kutatói pályázat |

|
Matematika és Számítástudományok Doktori Iskola
Témavezető: Simon Károly
Az internet matematikája – Hálózatmodellezés fraktálokkal
A kutatási téma néhány soros bemutatása
Kutatásom során az internet jövőjét érintő matematikai kutatási
kérdésekkel, elsősorban különböző hálózatmodellek matematikai vizsgálatával
foglalkozom. Célunk olyan modellek matematikai leírása, illetve megadása, melyek
különböző szempontokból jól modellezik a valós hálózatok bizonyos csoportjait:
például hierarchikus szerkezet mellett mutatnak skálafüggetlen eloszlást, vagy
közösségi hálózatot imitálandó, a hálózat erősen linkelt kisebb közösségekből
áll, melyeket gyenge élek tartanak össze. Hasonló modellek
nagy érdeklődésre tartanak számot mind a matematikai, mind az alkalmazott
tudományok körében.
A kutatóhely rövid bemutatása
A Sztochasztika
Tanszék Közép-Európa legerősebb, nemzetközi szinten elismert
kutatóhelye a valószínűségszámítás területén. Professzorai Szász Domokos (MTA alelnöke,
dinamikai rendszerek), Tóth Bálint (tanszékvezető,
véletlen bolyongások, sztochasztikus folyamatok) és Simon
Károly (OTKA Matematikai Bizottság elnök, véletlen és
determinisztikus fraktálok) kutatási témájuk legjelentősebb külföldi
folyóirataiban publikálnak és plenáris előadói témakörük legjelentősebb
nemzetközi konferenciáinak. A fiatalabb generációban olyan
nemzetközileg elismert docensek állnak, mint Balázs Márton (kölcsönható
részecskerendszerek), Tóth Péter (dinamikai rendszerek) és Székely
Balázs (alkalmazott valószínűségszámítás).
A Sztochasztika
Szeminárium hazánk kiemelkedően jeles valószínűségszámítási
szemináriuma, melyen a világ legnevesebb valószínűségszámítással foglalkozó
kutatói rendszeresen tartanak előadásokat. A tanszék
nagy hangsúlyt fektet a következő generáció nevelésére: nem véletlen, ha a kiváló kutatási
környezetben kiemelkedően magas a tanszéki témavezetéssel készült
diplomák, TDK-k száma, emellett a doktoranduszok rendkívül nagy létszáma is
jelzi, hogy támogató, segítő háttérrel gyümölcsöző munkát lehet folytatni. A
tanszékünkön végzett doktoranduszok jelentős része vezető USA-beli
és európai egyetemeken kap posztdoktori állást.
A kutatás történetének, tágabb kontextusának bemutatása
Az internet jövőjét érintő alapkutatásokra öt intézet (köztük a
BME Matematikai Intézet) közös konzorciális projektet nyert el OTKA NKTH 77778
számmal, melynek vezetője Simon Károly egyetemi tanár. E projekt
keretében kutatásom a jövő internetét érintő matematikai problémákkal
foglalkozik. Mivel ez egy új kutatási irány a tanszéken, ezért rendkívül
fontosnak tartottuk, hogy kapcsolatokat alakítsunk ki a témában kutató legfontosabb hazai és nemzetközi
csoportokkal. Ennek szellemében összesen három hónapot töltöttem a múlt évben a Microsoft
Research (Seattle) elméleti kutatócsoportjában. Célunkat,
hogy a témában folyó nemzetközileg fontos irányokkal megismerkedjünk, elértük. A csoport
vezetőjével, Yuval
Peres-zel két közös cikkem előkészületben van, továbbá Anna Karlinnal, a
University of Washington professzorával kialakított kapcsolat eredményezte egy
MSc és egy BSc diplomamunka témáját. Közös kutatásba kezdtünk Bollobás Béla
professzorral is, aki a véletlen gráfok témakörének egyik leghíresebb művelője a
világon. Ennek az együttműködésnek a kiinduló pontjául Kertész
János (BME, Fizika Intézet, complex
networks) által folytatott szociális hálózat-modellekhez kötődő
kutatások szolgáltak. Kapcsolatba léptünk Vicsek Tamással (ELTE) is. Az általa és
társszerzői által kidolgozott modell továbbfejlesztéséből írt cikkünket
elfogadták a Chaos,
Solitons and Fractals folyóiratban és a napokban kerül publikálásra. A
továbbiakban ennek a cikknek tartalmát mutatom be.
A kutatás célja, a megválaszolandó kérdések
Az elmúlt két évtizedben nagy tudományos figyelem fordult a komplex hálózatok (ilyenek többek között bizonyos biológiai, szociális hálózatok, illetve internetkapcsolat-hálózatok) modellezése felé. A kutatások több, különféle hálózatmodellhez vezettek, melyek a valós hálózatok különböző tulajdonságaira próbálnak közelítőleg jó modellel szolgálni. Általában cél, hogy egy véletlenszerűen kiválasztott csúcs fokáról (vagyis a belőle induló élek számáról) elmondhassuk, hogy eloszlása skálafüggetlen (hatványlecsengésű), azaz elég nagy fokú csúcsok is szerepeljenek a gráfban, de a csúcsok többségének igen kicsi legyen a fokszáma. Az ilyen típusú modellek között sok a véletlen, dinamikusan növekvő, úgynevezett preferenciális kapcsolódású modell. Teljesen más jellegű megközelítéssel élt Barabási, Ravasz és Vicsek, [1] akik egy determinisztikus, hierarchikus szerkezetű gráfsorozatot vezettek be, (lásd 1. ábra) mely a valós hálózatok hierarchikus felépítését, illetve a fokszámeloszlás skálafüggetlen jellegét tükrözte, egy bizonyos (γ=1+log 3/log 2) hatványkitevővel. A gráfsorozat egy enyhén módosított változata [2] pedig a valós hálózatok klaszterezettségét is jól modellezte, bár erre csak szimulációs eredmények voltak az irodalomban.
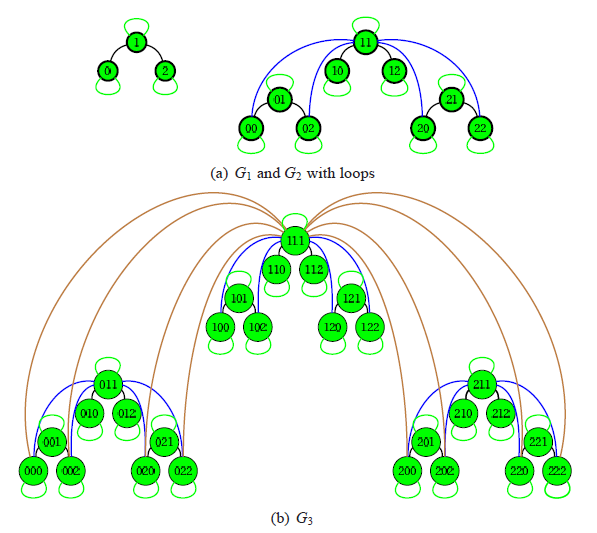
Kérdés volt, hogy lehet-e a modellt általánosítani, vagyis olyan hierarchikus szerkezetű gráfsorozatot megadni, mely fokszámeloszlásának γ hatványkitevője egy előre megadott érték (rendkívül érdekes eset, amikor a γ 1 és 2 közt van, ekkor ugyanis a fokszámeloszlásnak nincs várható értéke), illetve, hogyan lehet a modell determinisztikus jellegéből kilépve, közel hierarchikus szerkezetű véletlen gráfokat adott hatványkitevővel generálni. Továbbá célunk volt az is, hogy a már meglévő szimulációs eredményekre (lokális klaszterezettségi együttható, két véletlen pont közti legrövidebb út hossza, a gráf átmérője, stb.) korrekt matematikai bizonyítást adjunk.
Módszerek
A gráf csúcsainak megfelelő kódolása esetén a gráfhoz egyértelműen rendelhető, úgynevezett adjacencia mátrixot beskáláztuk az egységnégyzetbe (lásd ábra), majd ennek konvergenciáját bizonyítottuk. (A lenti ábrán egy négyzet teli, ha a megfelelő él az adott fenti gráfban jelen van. Az egymásnak megfelelő élek és négyzetek azonos színűek.) Beláttuk, hogy ez a halmazsorozat egy úgynevezett gráf-irányított önhasonló halmazhoz tart, melynek geometriai tulajdonságait a hozzá tartozó iterált függvényrendszer határozza meg.
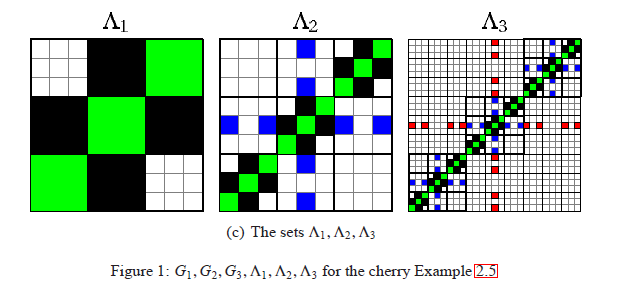
Így a gráfsorozatot sikerült lefordítanunk a fraktálok nyelvére:
a hierarchikus szerkezet annak felel meg, hogy a következő halmaz mindig az
előzőnek kicsinyített másolataiból áll, melyek a négyzet átlójában foglalnak
helyet, valamint az egyes kópiákat összekötő élek a diagonálon kívül jelennek
meg, és egy önhasonló fraktálhoz konvergálnak. Ezen új megközelítés segítségével
más kiinduló gráfokból is sikerült hasonló szabály szerint hierarchikus gráfokat
generálni, illetve tulajdonságaikat a csúcsok kódolásának köszönhetően a
fraktálból meghatározni.
Eddigi eredmények
Tetszőleges páros gráfból
kiindulva tudjuk definiálni a hozzá tartozó hierarchikus gráfsorozatot (egy példát mutat a jobb oldali ábra). A fokszámeloszlás
hatványkitevőjét a kiinduló gráf, illetve az egységnégyzetbe skálázott
adjacencia mátrixból származó fraktál ún. Hausdorff
dimenziója határozza meg: 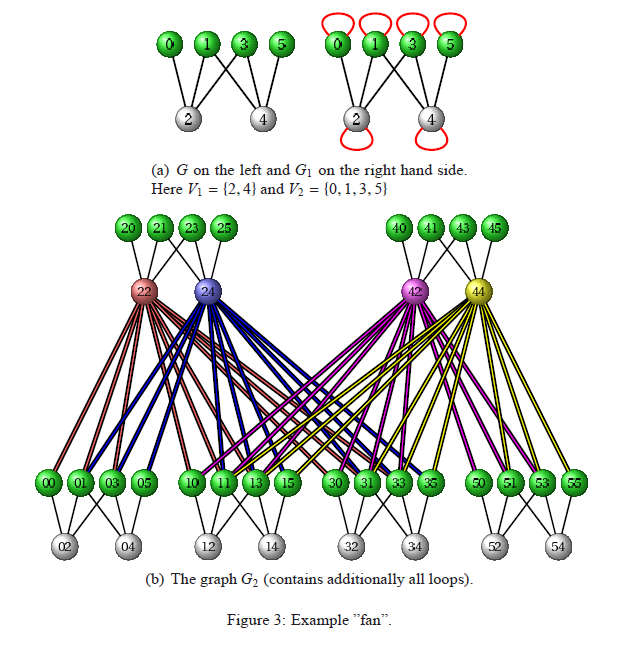
Különösen érdekes eset, ha a kiinduló gráfban
több él van, mint csúcs. Beláttuk, hogy ekkor a fokszámeloszlás γ kitevője egy hányados: a számláló a fraktálon átmenő
véletlen (meredekségű) egyenes és a fraktál metszetének Hausdorff dimenziója, a
nevező pedig a fraktálon átmenő függőleges egyenesnek és a fraktál
metszetének Hausdorff dimenziója
(lásd lenti ábra).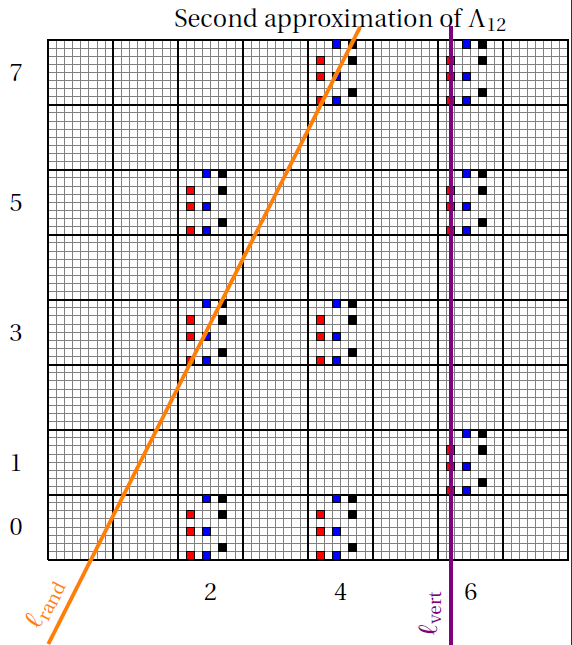
A csúcsok kódolását felhasználva
megmutattuk, hogy a gráf átmérője méretének logaritmusával arányos, illetve,
hogy két véletlen pont közötti legrövidebb út hosszának várható értéke is ekkora
nagyságrendű. Az enyhén módosított modellt vizsgálva bebizonyítottuk, hogy a
gráfok lokális klaszterezettségi együtthatójának nagyságrendje a csúcs
fokszámának reciproka, ezzel bizonyítva a szimuláción alapuló érveléseket.
Végül a modellt véletlenítettük is, melynek
valószínűségszámítási interpretációja a következő lehet: képzeljük azt, hogy a
determinisztikus gráf minden csúcsának helyén egy-egy urna található. Vegyünk
most elég sok golyót, legalább annyit, hogy minden urnába átlagosan annyi
jusson, mint az eredeti legkisebbik gráfunk. Ezeket a golyókat dobjuk be az
urnákba, mindegyiket véletlenszerűen és egymástól függetlenül. A véletlen
gráfunk úgy keletkezik, hogy két csúcsot összekötünk, ha a nekik megfelelő
golyók egymással összekötött vagy azonos urnában landoltak. Az így keletkező
gráfról beláttuk, hogy fokszámeloszlásának lecsengése (nagy valószínűséggel)
ugyanolyan γ hatványkitevőjű, mint az eredeti gráfé volt.
Várható impakt, további kutatás
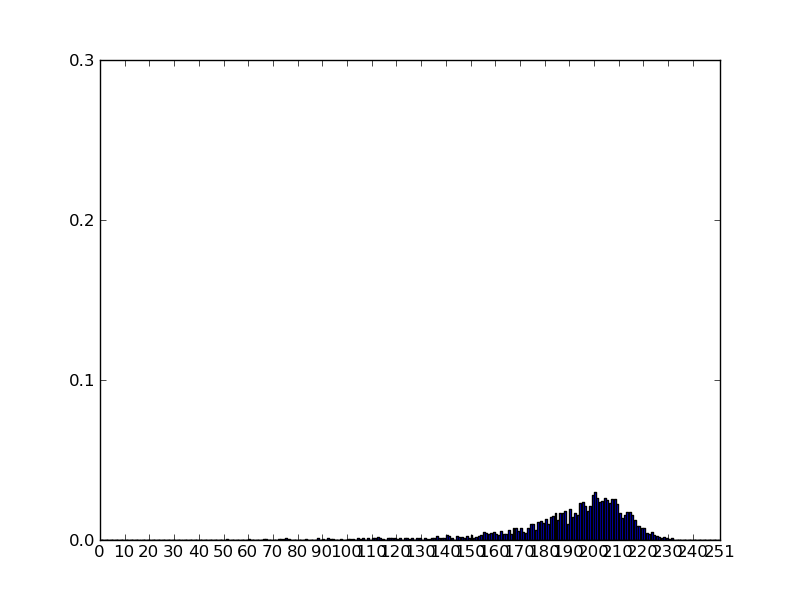
Az itt bemutatott modellről írt cikkünk
a napokban jelenik meg a Chaos, Solitons and Fractals (3.32 impaktfaktorú)
folyóiratban. A továbbiakban a témában a Kertész Jánostól és
kutatócsoportjától származó modell matematikai vizsgálatát folytatjuk. Ez
egy dinamikusan fejlődő, szociális közösségi hálózatmodell, melyben a
kapcsolatok kis közösségekben erősek, a közösségek közti kapcsolatok gyengék.
Érdekes kérdés, hogy mennyi idő alatt stabilizálódik a legnagyobb közösség
eloszlása, illetve milyen jellegű ez az eloszlás. A grafikonon sokezer
szimulációból származóan a legnagyobb komponens eloszlását látjuk, miután már
stabilizálódott.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája
[A] Komjáthy
J, Simon K., Generating hierarchial scale-free graphs from fractals. Chaos,
Solitons & Fractals
(2011), doi:10.1016/j.chaos.2011.05.012
[B] J. Komjathy, J. Miller, Y. Peres, A tight bound of the uniform mixing time of lamplighter walks. Előkészületben.
Linkgyűjtemény
Sztochasztika Szeminárium,
BME
Internet Jövője Matematika Szeminárium
Microsoft Research, Theory Group honlapja
Complex Networks
kutatócsoport, Elméleti Fizika Tanszék, BME
Hivatkozások listája
[1]
A.-L. Barabási, E. Ravasz, T. Vicsek, Deterministic Scale-Free Networks,
Physica
A: Statistical Mechanics and its Applications 299, Issues 3-4 559-564
(2001) 559–
564.
[2]
E. Ravasz, A.-L. Barabási, Hierarchical organization in complex networks,
Phys.
Rev. E 67 (2003) 47 026112.
[3] B. Bollobás, Random graphs, Cambridge University Press,
2001.
