 |
BMe Research Grant |

|
Doctoral School of Information Science and Technology
Budapest University of Technology and Economics (BUTE)
Faculty of Electrical Engineering and Informatics
Department of Telecommunications
Supervisor: Prof. Dr. IMRE, Sandor (DSc), Professor, Head of Department, Department of Telecommunications
Quantum Repeaters with Superactivated Quantum Channels
Introducing the research area
The superactivation of zero-capacity quantum channels makes it possible to use two zero-capacity quantum channels with a positive joint capacity at the output. Currently, we have no theoretical background for describing all possible combinations of superactive zero-capacity channels, hence there should be many other possible combinations. In my work, I give an algorithmic solution to the problem. I also present a fundamentally new idea, which enhances the efficiency of the quantum repeaters.

Brief introduction of the research place
The Department of Telecommunications of Budapest University of Technology and Economics in Hungary has been providing a solid ground for teaching, researching and developing information and communication technologies for more than 60 years. The primary fields covered by the Department are acoustics, cryptography, computing (both classical and quantum), multimedia, networking and signal processing.
History and context of the research
In the case of a classical channel, we can send only classical information. Quantum channels extend the possibilities, and we can send classical information, entanglement assisted classical information, private information and of course, quantum information.

Fig. 1. Quantum channels can be implemented in practice very easily, e.g. via the current optical fiber networks (or by wireless optical channels), and make it possible to transfer various types of information.
On the other hand, the elements of classical information theory cannot be applied in the case of quantum information, i.e., they can only be used in some special cases.
Superactivation cannot be imagined for classical systems. In the near future, superactivation can revolutionize communication over long-distances, and it can help enhance the security of quantum communication and the performance of quantum repeaters.
The problem of superactivation of zero-error capacity quantum channels can be viewed as a smaller subset of a larger problem set involving the additivity of quantum channels and the superactivation of quantum channels.
There is no general formula to describe the additivity property of every quantum channel model, but one of the main results of the recent researches was the “very simplified” picture, that the various capacities (i.e. classical, private, quantum) of a quantum channel are all non-additive.
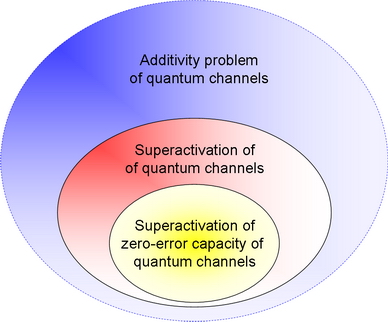
Fig. 2. The problem of superactivation of zero-error capacity of quantum channels as a sub domain of larger problem sets. [L. Gyongyosi, S. Imre. Algorithmic Superactivation of Asymptotic Quantum Capacity of Zero-Capacity Quantum Channels. Information Sciences, Informatics and Computer Science Intelligent Systems Applications, ELSEVIER, ISSN: 0020-0255; 2011]
Superactivation can be applied to an optical-fiber based optical quantum communication network or in a free-space environment, both in a dense metropolitan area or over very long distances to improve the quality of information transmission.
Our method can be a very valuable tool to realize zero-error quantum communication over a noisy communication environment.
Using the superactivation of quantum channels, the effectiveness of the communication techniques in future quantum networks - over long-distances, or in a noisy metropolitan area - can be increased, and the currently used communication techniques can be revolutionized.

Fig. 3. The quantum channels have zero capacities individually, but jointly they define a structure which can be used to transmit information. [G. Smith, J. Yard. Quantum Communication with Zero-capacity Channels. Science 321, 1812-1815 (2008)]
In addition to aiding metropolitan and long-distance quantum communication, the perfect information transmission through a quantum channel can have deep relevance both in military and secret government applications, or other cases where extremely high security is required.
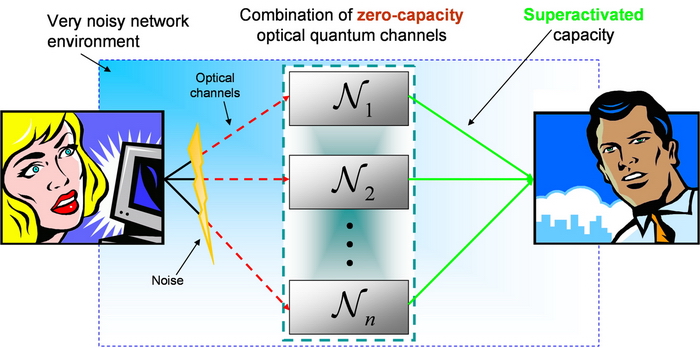
Fig. 4. Combination of quantum channels with individual zero-error capacity, to realize perfect information transmission. [L. Gyongyosi, S. Imre. Information Geometric Superactivation of Classical Zero-Error Capacity of Quantum Channels. Progress in Informatics, Quantum Information Technology, Print ISSN : 1349-8614, Online ISSN : 1349-8606; 2011.]
The research goal, open questions

The computation of the capacity of quantum channels is an extremely difficult and hard computational problem, as has been stated by Beigi and Shor in 2007.
Fig. 5. Computation of quantum channel capacity is numerically hard. [S. B, P. W. Shor. On the Complexity of Computing Zero-Error and Holevo Capacity of Quantum Channels. arXiv:0709.2090 [quant-ph] (2007)]
The proposed solution avoids this problem. I show a fundamentally new method of finding the conditions for the superactivation of asymptotic quantum capacity and classical zero-error capacity of zero-capacity quantum channels..
In practice, to discover these superactive zero-capacity channel-pairs, we have to analyze an extremely large set of possible quantum states, channel models and channel probabilities.
Currently we have no theoretical background for describing all possible combinations of superactive zero-capacity quantum channels, hence there should be many other possible combinations.
Moreover:
The proposed method can be a very valuable tool for improving the results of fault-tolerant quantum computation and possible communication techniques over very noisy quantum channels.

The proposed method can be the first efficient algorithmic solution to discover the still unknown combinations to determine the superactivation of the zero-error (perfect information transmission) capacity of quantum channels, without extremely high computational costs.
In Fig. 6, we illustrate the logical
structure of the analysis and the cooperation
of classical and quantum systems.
We would like to analyze the properties of quantum channels using current classical computer architectures – since currently we have no quantum computers – and the most efficient algorithms currently available. To this day, the most efficient classical algorithms for this purpose are computational geometric methods.
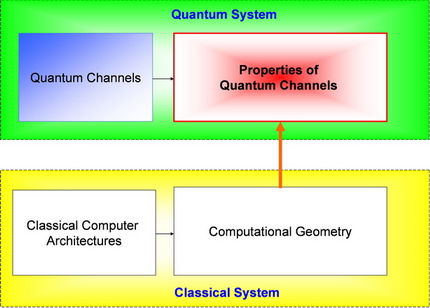
Fig. 6. The logical structure of our analysis. We use current classical architectures to analyze the properties of quantum channels. [L. Gyongyosi, S. Imre. Algorithmic Superactivation of Asymptotic Quantum Capacity of Zero-Capacity Quantum Channels. Information Sciences, Informatics and Computer Science Intelligent Systems Applications, ELSEVIER, ISSN: 0020-0255; 2011]
Methodology: Information-Geometric Solution of Superactivation
I developed an information-geometric method of finding
the conditions for the superactivation of zero-capacity quantum
channels.
The proposed information-geometric solution can be the
first efficient algorithmic solution to discover the still unknown combinations
to determine the superactivation of the zero-error capacity of quantum
channels, without the extremely high
computational costs.
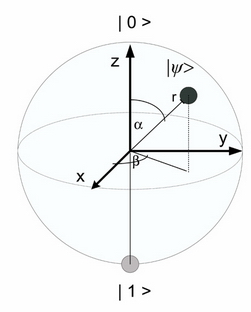
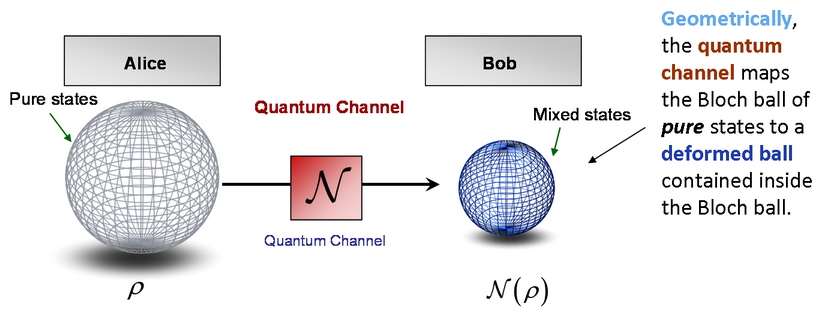
Fig. 7(a): The quantum states can be represented geometrically on the Bloch sphere. (b): The superactivation property of the zero-capacity optical quantum channels can be described as the radii of the smallest enclosing quantum information ball. [L. Gyongyosi, S. Imre. Information Geometric Security Analysis of Differential Phase Shift QKD Protocol. Security and Communication Networks, John Wiley & Sons, Ltd. ISSN: 1939-0114; 2010.]
The capacity of the analyzed quantum channel is equal to the radius of the smallest enclosing ball.
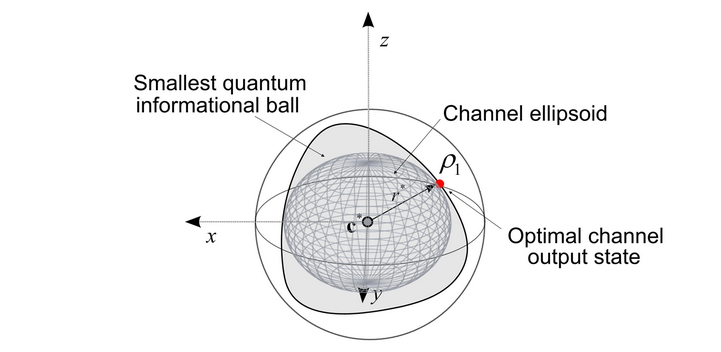
Fig. 8. The channel ellipsoid of the unital quantum channel model. The center of the channel ellipsoid and the smallest quantum informational ball is equal to the center of the of the Bloch sphere. [L. Gyongyosi, S. Imre. Informational Geometric Analysis of Superactivation of Zero-Capacity Optical Quantum Channels. SPIE Photonics West OPTO 2011, Advanced Quantum and Optoelectronic Applications, "Advances in Photonics of Quantum Computing, Memory, and Communication IV", Section on Quantum Communication, Jan. 2011, San Francisco, California, USA.]
Geometrically, the smallest quantum informational ball can be computed from the intersection of contours of the quantum relative entropy ball with the ellipsoid of the channel, whose ellipsoid is generated by the map of the channel.

Fig. 9(a): The average state does not lie inside the channel ellipsoid, (b): the quantum ball does not intersect the channel ellipsoid, (c): the length of the radius of the quantum ball is not acceptable.
[L. Gyongyosi, S. Imre. Information Geometric Superactivation of Classical Zero-Error Capacity of Quantum Channels. Progress in Informatics, Quantum Information Technology, Tokyo, Japan, Print ISSN : 1349-8614, Online ISSN : 1349-8606; 2011.]
The average state and the optimal output state are interpreted from the meaning of channel capacity, which states are available after the joint measurement.
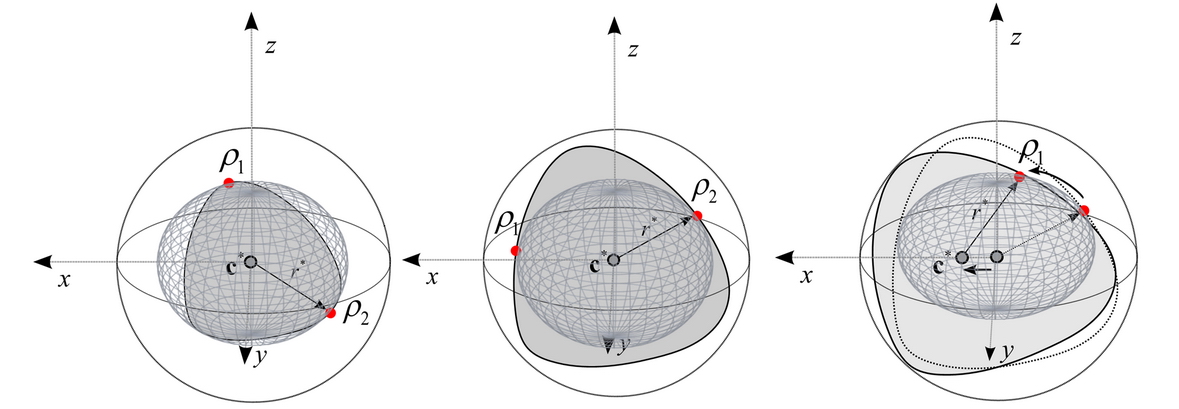
Fig. 10(a): The algorithm did not realize the maximization criteria in the iteration, (b): an acceptable situation, when the smallest enclosing quantum informational ball intersects both of the channel endpoints, (c): by moving the optimal average state, the radius of the smallest enclosing quantum informational ball will increase. [L. Gyongyosi, S. Imre. Information Geometric Superactivation of Classical Zero-Error Capacity of Quantum Channels. Progress in Informatics, Quantum Information Technology, Tokyo, Japan, Print ISSN : 1349-8614, Online ISSN : 1349-8606; 2011.]
Superactivation of Optical Quantum Channels
In my works I analyzed the superactivation of optical quantum channels. Optical quantum channels are of high importance in physical applications, since they describe the energy dissipation due to losing a particle.
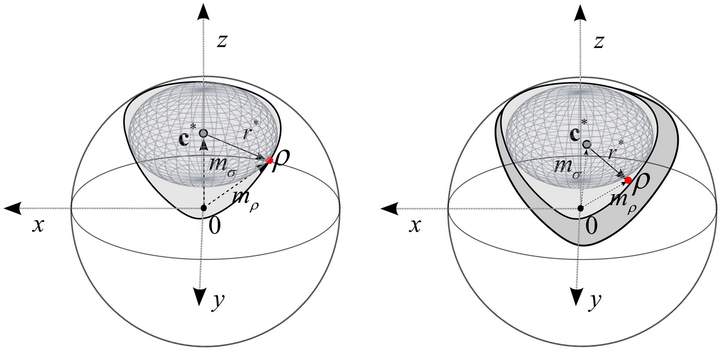
Fig. 11. Intersection of quantum informational ball and channel ellipsoid of amplitude damping channel and the movement of the optimal ball. [L. Gyongyosi, S. Imre. Information Geometrical Analysis of Additivity of Optical Quantum Channels. IEEE/OSA Journal of Optical Communications and Networking (JOCN), IEEE Photonics Society & Optical Society of America, ISSN: 1943-0620; 2010.]
We introduced the quantum-Delaunay triangulation to compute the convex hull of channel output quantum states. Delaunay triangulation can be used to find the smallest enclosing ball of a set of quantum states in the quantum space. The channel output states are denoted by their density matrices.
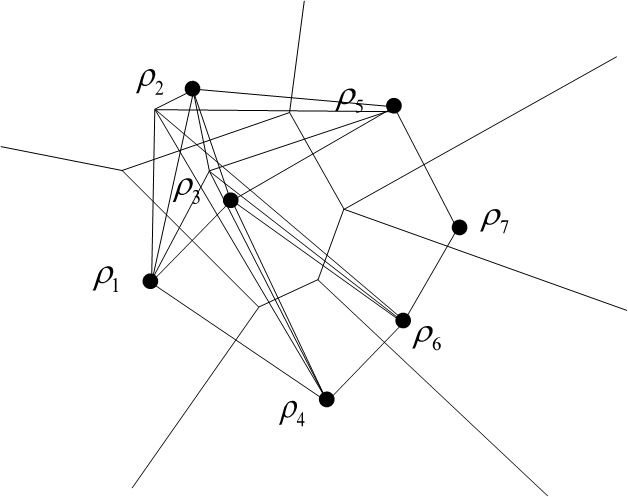
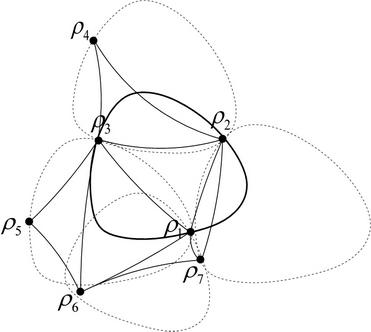
Fig. 12. Comparison of classical Euclidean (a) and quantum Delaunay triangulation (b). [L. Gyongyosi, S. Imre. Algorithmical Analysis of Information-Theoretic Aspects of Secure Communication over Optical-Fiber Quantum Channels. Journal of Optical and Fiber Communications Research, Springer New York, ISSN 1867-3007, 1619-8638; 2010.]
From the convex hull, the quantum informational ball can be derived, which will be used in the analysis of superactivation.
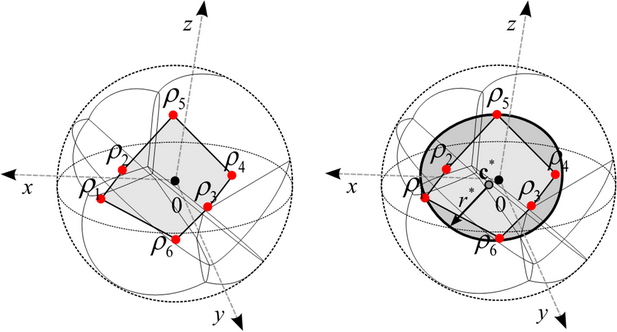
Fig. 13. The three-dimensional convex hull (light-grey) of channel output states, and the smallest quantum informational ball (grey).
Moreover, the method can be used to analyse the superactivation of practical quantum communication channels, such as optical fibers.
.
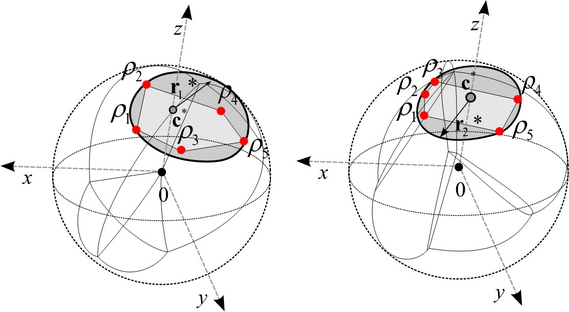
Fig. 14. Quantum Capacity Analysis of Optical Quantum Communication Channels. [L. Gyongyosi, S. Imre. Information Geometrical Analysis of Additivity of Optical Quantum Channels, IEEE/OSA Journal of Optical Communications and Networking (JOCN), IEEE Photonics Society & Optical Society of America, ISSN: 1943-0620; 2010.]
To analyze the superactivation of quantum channels, I
introduce a new geometrical representation, called the quantum superball.
The superactivation of quantum channels is analyzed by the quantum informational superball.
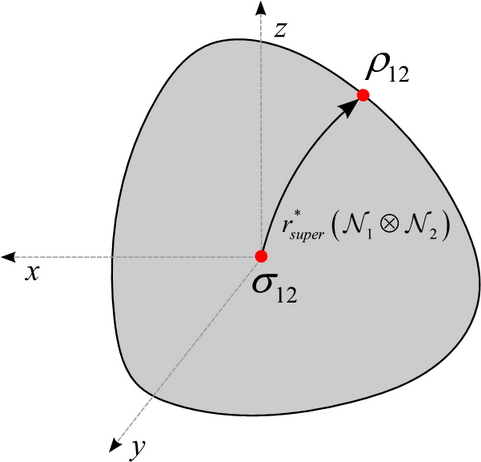
Fig. 15. The abstract quantum superball for analysis of superactivation. [L. Gyongyosi, S. Imre. Information Geometric Superactivation of Zero-Capacity Quantum Channels. The Second International Conference on Quantum Information and Technology - New Trends in Quantum Information Technology (ICQIT2010), Quantum Information Science Theory Group (QIST), 2010, QIST, NII, Tokyo, Japan.]
Expected impact and further research
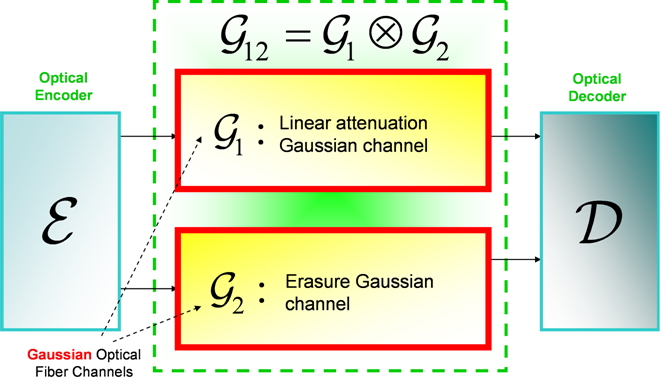
Fig. 16. Zero-error information transmission with very noisy Gaussian optical fiber quantum channel. Although these quantum channels have zero zero-error capacities individually, jointly they define a structure which can be used to transmit classical information perfectly. [L. Gyongyosi, S. Imre. Zero-Error Transmission of Classical Information with Zero-Capacity Gaussian Quantum Channels. In Preparation, 2011]
There are several differences between a classical and a quantum repeater. Quantum repeaters are not simply signal amplifiers, in contrast the classical repeaters.
Quantum repeaters are based on the transmission of entangled quantum states between the repeater nodes.
The main task is the improvement of the fidelity of shared entangled states.
The creation of high-fidelity entanglement between the nodes requires a lot of entangled pairs, while the purification process is a computationally very complex.
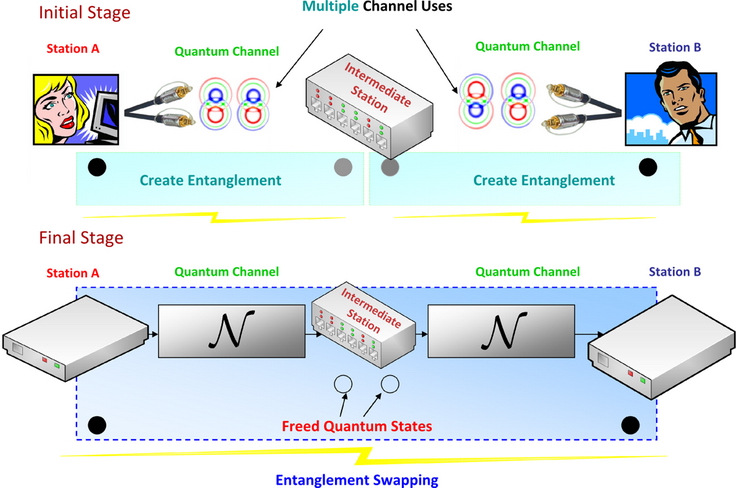
Fig. 17. The standard model of the quantum repeater with noisy quantum channels. The structure of the quantum repeater consists of a chain of base stations and the information is transmitted via quantum teleportation. [L. Gyongyosi, S. Imre. Efficient Quantum Repeaters without Entanglement Purification. International Conference on Quantum Information (ICQI) 2011, (The Optical Society of America (OSA), University of Rochester), Jun. 2011, University of Ottawa, Ottawa, Canada.]
The most important part of quantum communication between quantum repeaters is the entanglement purification. This step purifies the noisy quantum states, however, this process requires a lot of resources in the quantum nodes, and it cannot be implemented efficiently in current solutions.
The efficiency of the quantum repeaters in future would be incremental only if the efficiency of purification process could be dramatically increased.
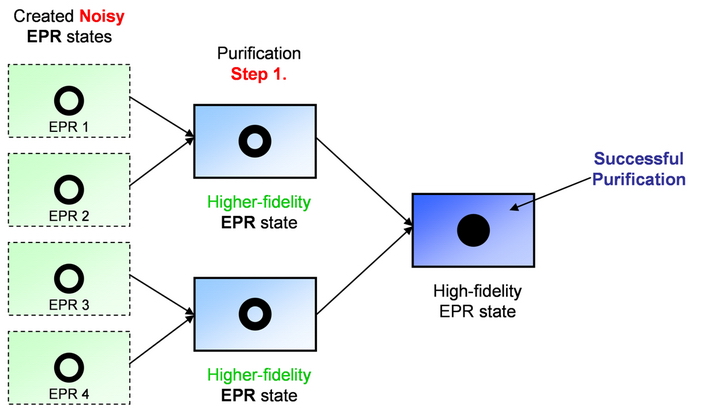
Fig. 18. The entanglement purification process. From two purified states a higher fidelity EPR state can be generated.
I present a fundamentally new idea, which enhances the efficiency of the quantum repeaters.
I show, that with the help of superactivation, the efficiency of quantum repeater can be increased extremely, and entanglement purification can almost completely be removed from the current inefficient solutions, which opens new perspectives in future long-distance quantum communications [L. Gyongyosi, S. Imre. Quantum Repeaters with Superactivated Gaussian Optical Fiber Quantum Channels. In Preparation, 2011].
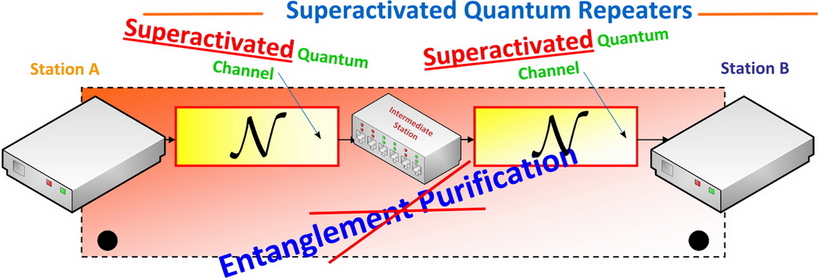
Fig. 19. Our newly developed quantum repeater with noisy quantum channels and perfect information transmission. [L. Gyongyosi, S. Imre. Efficient Quantum Repeaters without Entanglement Purification. International Conference on Quantum Information (ICQI) 2011, (The Optical Society of America (OSA), University of Rochester), Jun. 2011, University of Ottawa, Ottawa, Canada.]
The newly developed quantum repeater uses noisy quantum channels such as in the case of standard quantum repeaters.
On the other hand, these quantum channels can be used for perfect information transmission, and the entangled quantum states can be sent through the channels with maximal fidelity. As a conclusion, no further purifications needed during the communication.
The efficiency of quantum repeaters in long distance communication will be the most important questions in future telecommunications, in global-scale cryptography and in distributed communications.
Since the development of the theoretical background of quantum communication with noisy quantum channels will be one of the most important questions in future communications, the proposed research work will be of interest to scientists in other fields.
The full list of publications and conference papers can be found at: www.hit.bme.hu/~gyongyosi/.
References
[S. B, P. W. Shor. On the Complexity of Computing Zero-Error and Holevo Capacity of Quantum Channels. arXiv:0709.2090 [quant-ph] (2007)][G. Smith, J. Yard. Quantum Communication with Zero-capacity Channels. Science 321, 1812-1815 (2008)]
[R. Duan. Superactivation of zero-error capacity of noisy quantum channels. arXiv:0906.2527, (2009)]
[T. S. Cubitt, Graeme Smith. Super-Duper-Activation of Quantum Zero-Error Capacities. arXiv:0912.2737v1. (2010).]
[T. Cubitt, J. X. Chen, and A. Harrow. Superactivation of the Asymptotic Zero-Error Classical Capacity of a Quantum Channel. arXiv: 0906.2547. (2009)]
Results
The results have been published in journals and conferences
- University of Cambridge (Cambridge, UK),
- University of Harvard (Cambridge, USA),
- University of Berkeley (California, USA),
- Princeton University (New Jersey, USA),
- University of Arizona (Arizona, USA);
- University of Ottawa (Canada)
- University of Queensland (Australia),
- University of Southampton (UK),
- National Institute of Informatics, Tokyo (Japan),
- Nanyang Technological University, (Singapore).
The results on additivity and superactivation analysis of quantum channels have been published in many journals (published by IEEE, Elsevier, Springer, Wiley, etc., see www.hit.bme.hu/~gyongyosi/).
I obtained two Best Paper Awards on international conferences related to future computing and quantum information processing at University of Harvard, USA, and a Best Paper Award 2009 - "Pollak-Virag" - from the Scientific Association for Infocommunication (Hungary), and in 2010 a PhD Grant from the University of Arizona.
See the list of Publications and Conferene Papers, or www.hit.bme.hu/~gyongyosi/.
Publications
Journal Publications
1. Laszlo Gyongyosi, Sandor Imre. Information Geometric Superactivation of Classical Zero-Error Capacity of Quantum Channels, Progress in Informatics, Quantum Information Technology, Quantum Information Science Theory Group, National Institute of Informatics (NII, 国立情報学研究所), Tokyo, Japan, Print ISSN: 1349-8614, Online ISSN : 1349-8606; accepted. (2011.)
2. Laszlo Gyongyosi, Sandor Imre. Algorithmic Superactivation of Asymptotic Quantum Capacity of Zero-Capacity Quantum Channels, Information Sciences, Informatics and Computer Science Intelligent Systems Applications, ELSEVIER, ISSN: 0020-0255; accepted. (2011.)
3. Laszlo Gyongyosi, Sandor Imre. Capacity Recovery of Very Noisy Optical Quantum Channels,International Journal of Applied Mathematics and Informatics, University Press, ISSN: 2074-1278, United Kingdom; 2011.
4. Laszlo Gyongyosi, Sandor Imre. Information Geometrical Analysis of Additivity of Optical Quantum Channels, IEEE/OSA Journal of Optical Communications and Networking (JOCN), IEEE Photonics Society & Optical Society of America, ISSN: 1943-0620; 2010, accepted.
5. Laszlo Gyongyosi, Sandor Imre. Algorithmical Analysis of Information-Theoretic Aspects of Secure Communication over Optical-Fiber Quantum Channels, Journal of Optical and Fiber Communications Research, Springer New York, ISSN 1867-3007 (Print) 1619-8638 (Online); 2010, accepted.
6. Laszlo Gyongyosi, Sandor Imre. Information Geometric Security Analysis of Differential Phase Shift QKD Protocol, Security and Communication Networks, John Wiley & Sons, Ltd. ISSN: 1939-0114; 2010, accepted.
7. Laszlo Gyongyosi, Sandor Imre. Novel Quantum Information Solution to Copy-Protection and Secured Authentication, International Journal of Internet Technology and Secured Transactions (IJITST), ISSN (Online): 1748-5703, ISSN (Print): 1748-569X; 2011, accepted.
8. Laszlo Gyongyosi, Sandor Imre. Informational Geometric Analysis of Superactivation of Asymptotic Quantum Capacity of Zero-Capacity Optical Quantum Channels, Proceedings of SPIE Photonics West OPTO 2011, ISBN: 9780819484857, Vol: 7948.
9. Laszlo Gyongyosi, Sandor Imre. Information Geometric Solution to Additivity of Amplitude-Damping Quantum Channel, AIP Conference Proceedings of QCMC 2010, American Institute of Physics, AIP Conference Proceedings Series (Library of Congress), 2011.
10. Laszlo Gyongyosi, Sandor Imre. Quantum Informational Divergence in Quantum Channel Security Analysis, International Journal of Network Security, ISSN 1816-353X, ISSN 1816-3548; 2011, accepted.
11. Laszlo Gyongyosi, Sandor Imre. Efficient Computational Information Geometric Analysis of Physically Allowed Quantum Cloning Attacks for Quantum Key Distribution Protocols, WSEAS Transactions on Communications, ISSN: 1109-2742; 2010, accepted.
12. Laszlo Gyongyosi, Sandor Imre. Information Geometrical Approximation of Quantum Channel Security, International Journal On Advances in Security, Published by: International Academy, Research and Industry Association, ISSN: 1942-2636; 2010., accepted.
13. Laszlo Gyongyosi, Sandor Imre. Geometrical Estimation of Information Theoretical Impacts of Incoherent Attacks for Quantum Cryptography, International Review of PHYSICS, Print ISSN: 1971 - 680X; 2010, accepted.
14. Laszlo Gyongyosi, Sandor Imre. Quantum Singular Value Decomposition Based Approximation Algorithm, Journal of Circuits, Systems, and Computers (JCSC), World Scientific, Print ISSN: 0218-1266, Online ISSN: 1793-6454; 2010, accepted.
15. Laszlo Gyongyosi, Sandor Imre. Quantum Information Theoretical Based Geometrical Representation of Eavesdropping Activity on the Quantum Channel, Infocommunications Journal, Scientific Association for Infocommunications, ISSN 0018-2028; 2010, accepted.
16. Laszlo Gyongyosi, Sandor Imre. Quantum Protected Software, International Review on Computers and Software, ISSN:1828-6003, 1828-6011; 2009, accepted.
17. Laszlo Gyongyosi, Sandor Imre. Quantum cryptography based info-communication systems,Info-Communications Technology, Scientific Association for Infocommunications, BUTE, Faculty of Electrical Engineering and Informatics, Department of Telecommunications, 2008. ISSN 0018-2028; Best Paper Award 2009 - "Pollak-Virag" - from the Scientific Association for Infocommunication (Hungary).
18. Laszlo Gyongyosi. Quantum information in data privacy, Alma Mater series, Studies on Information and Knowledge Processes: Open Data, Protected Data 2, pages 341–378., BUTE, Faculty of Economic and Social Sciences, ISSN 1587-2386, ISBN 798-963-87788-5-7; 2008
19. Laszlo Gyongyosi. TOR and Torpark: Functional and performance analyses of new generation anonymous browsers, Alma Mater series, Studies on Information and Knowledge Processes 11, pages 159-191., BUTE, Faculty of Economic and Social Sciences, 2007. ISSN 1587-2386, ISBN-10 963-421-429-0, ISBN-13 987-963-421-429-8. Published on-line: Hungarian privacy Enhancing Technologies portal.
In Preparation (2011)
L. Gyongyosi, S. Imre. Zero-Error Transmission of Classical Information with Zero-Capacity Gaussian Quantum Channels, 2011.
L. Gyongyosi, S. Imre. Photonic Entanglement for Perfect Transmission of Quantum Information, 2011.
L. Gyongyosi, S. Imre. Quantum Repeaters with Superactivated Gaussian Optical Fiber Quantum Channels, 2011.
L. Gyongyosi, S. Imre. Pilot Quantum Error Correction, 2011.
L. Gyongyosi, S. Imre. The Kerosene Classical Capacity of a Quantum Channel, 2011.
Book
Sandor Imre and Laszlo Gyongyosi. Advanced Quantum Communications - An Engineering Approach, Publisher: Wiley-IEEE Press (New Jersey, USA), John Wiley & Sons, Inc., The Institute of Electrical and Electronics Engineers. (In preparation, date expected: 2011.)
Book Chapters
1. Laszlo Gyongyosi, Sandor Imre. Quantum Cryptographic Protocols and Quantum Security, in "Cryptography: Protocols, Design and Applications", Nova Science Publishers, USA,. (In preparation, date expected: 2011.)
2. Laszlo Gyongyosi, Sandor Imre. Secure Long-Distance Quantum Communication over Noisy Optical Fiber Quantum Channels, in "Optical Fibers", INTECH, ISBN 978-953-307-922-6; (In preparation, date expected: 2011.)
3. Laszlo Gyongyosi, Sandor Imre. Quantum Cellular Automata Controlled Self-Organizing Networks, in"Cellular Automata", INTECH, ISBN 978-953-7619-X-X; 2010.
4. Laszlo Bacsardi, Laszlo Gyongyosi, Marton Berces, Sandor Imre. Quantum Solutions for Future Space Communication, in "Quantum Computers", Nova Science Publishers, 2010.
5. Sandor Szabo, Laszlo Gyongyosi, Karoly Lendvai, Sandor Imre. Overview of IP Multimedia Subsystem Protocols and Communication Services, in "Advanced Communication Protocol Technologies: Solutions, Methods and Applications", 2010.
Conferences
1. Laszlo Gyongyosi, Sandor Imre. “Efficient Quantum Repeaters without Entanglement Purification, International Conference on Quantum Information (ICQI), The Optical Society of America (OSA), June 6-8 2011, University of Ottawa, Ottawa, Canada.
2. Laszlo Gyongyosi, Sandor Imre. Channel Capacity Restoration of Noisy Optical Quantum Channels, ICOAA '11 Conference, Section on Optical Quantum Communications, Febr. 2011, University of Cambridge, Cambridge, United Kingdom.
3. Laszlo Gyongyosi, Sandor Imre. Informational Geometric Analysis of Superactivation of Zero-Capacity Optical Quantum Channels, SPIE Photonics West OPTO 2011, Advanced Quantum and Optoelectronic Applications, "Advances in Photonics of Quantum Computing, Memory, and Communication IV", Section on Quantum Communication, Jan. 2011, The Moscone Center, San Francisco, California, USA.
4. Laszlo Gyongyosi, Sandor Imre. Algorithmic Solution to Superactivation of Zero-Capacity Optical Quantum Channels, Photonics Global Conference (PGC) 2010, Nanyang Technological University, IEEE Photonics Society, Nature Photonics, 2010, Suntec City, Singapore, accepted.
5. Laszlo Gyongyosi, Sandor Imre. Information Geometric Superactivation of Zero-Capacity Quantum Channels, The Second International Conference on Quantum Information and Technology - New Trends in Quantum Information Technology (ICQIT2010), Quantum Information Science Theory Group (QIST), National Institute of Informatics (NII), National Institute of Information and Communications Technology (NICT), 2010, Tokyo, Japan, accepted.
6. Laszlo Gyongyosi, Sandor Imre. Capacity Recovery of Useless Photonic Quantum Communication Channels, ALS Conference, Lawrence Berkeley National Laboratory (Berkeley Lab), University of California, Berkeley (California), USA, 2010, accepted.
7. Laszlo Gyongyosi, Sandor Imre. Method for Discovering of Superactive Zero-Capacity Optical Quantum Channels, IONS-NA Conference, (Optical Society of America (OSA), American Physical Society (APS), SPIE—The International Society for Optical Engineering, Rochester Institute of Optics, University of Maryland), 2010, University of Arizona, Tucson (Arizona), USA, accepted.
8. Laszlo Gyongyosi, Sandor Imre. Information Geometrical Solution to Additivity of Non-Unital Quantum Channels, QCMC 2010, 10th Quantum Communication, Measurement & Computing Conference, Section on Quantum Computing and Quantum Information Theory (Centre for Quantum Computer Technology) July 2010, University of Queensland, Brisbane, Queensland, Australia, accepted.
9. Laszlo Gyongyosi, Sandor Imre. Computational Information Geometric Analysis of Quantum Channel Additivity, Photon10 Conference, Quantum Electronics Group (QEP-19), Section on Quantum information, University of Southampton, Institute of Physics (IOP) Optics and Photonics Division, 2010, Southampton, UK, accepted.
10. Laszlo Gyongyosi, Sandor Imre. Novel Geometrical Solution to Additivity Problem of Classical Quantum Channel Capacity, The 33rd IEEE Sarnoff Symposium - 2010, IEEE Princeton/Central Jersey Section, Princeton University, Apr. 2010, Princeton, New Jersey, USA, accepted.
11. Laszlo Gyongyosi, Sandor Imre. Computational Geometric Analysis of Physically Allowed Quantum Cloning Transformations for Quantum Cryptography, International Conference on Computer Engineering and Applications, Section on Quantum Computing, (The World Scientific and Engineering Academy and Society, CEA '10), 2010, University of Harvard, Cambridge (Massachusetts), USA, accepted. BEST PAPER AWARD 2010, Harvard University, Cambridge, USA.
12. Laszlo Bacsardi, Laszlo Gyongyosi, Sandor Imre. Using Redundancy-free Quantum Channels for Improving the Satellite Communication, PSATS 2010, 2nd International ICST Conference on Personal Satellite Services, Section on Satellite Quantum Communications, 4-6 February 2010, Rome, Italy, accepted. Lecture Notes of The Institute for Computer Sciences Social-Informatics and Telecommunications Engineering (ISSN: 1867-8211) (2010)
13. Laszlo Gyongyosi, Sandor Imre. Quantum Informational Geometry for Secret Quantum Communication, The First International Conference on Future Computational Technologies and Applications, FUTURE COMPUTING 2009, Section on Quantum Computing, International Academy, Research and Industry Association, 2009, Athens, Greece, accepted. FUTURE COMPUTING 2009: Best Paper Award.
14. Laszlo Gyongyosi, Laszlo Bacsardi, Sandor Imre. Novel Approach for Quantum Mechanical Based Autonomic Communication, The First International Conference on Future Computational Technologies and Applications, FUTURE COMPUTING 2009, Section on Quantum Computing, International Academy, Research and Industry Association, 2009, Athens, Greece, accepted.
15. Laszlo Bacsardi, Laszlo Gyongyosi, Sandor Imre. Solutions For Redundancy-free Error Correction In Quantum Channel, International Conference on Quantum Communication and Quantum Networking, October 26 – 30, 2009, Vico Equense, Sorrento peninsula, Naples, Italy, accepted.
16. Laszlo Gyongyosi, Sandor Imre. Quantum Divergence based Quantum Channel Security Estimation, N2S’2009 International Conference on Network and Service Security, Section on Quantum Cryptography and QKD, IFIP TC6 WG, IEEE France, June, 2009. Paris, France, accepted.
17. Laszlo Gyongyosi, Sandor Imre. Unduplicable Quantum Data Medium Based Secret Decryption and Verification, The 4th International Conference for Internet Technology and Secured Transactions (ICITST-2009), November 9-12, 2009, IEEE UK & RI, London, United Kingdom, accepted.
18. Laszlo Gyongyosi, Sandor Imre. Fidelity Analysis of Quantum Cloning Attacks in Quantum Cryptography, ConTEL 2009 International Conference on Telecommunications, IEEE Communications Society, 2009. Zagreb, Croatia, accepted.
19. Laszlo Gyongyosi. Really unbreakable? The Security Analysis of Quantum Cryptography, Hacktivity conference 2008, Budapest
20. Laszlo Gyongyosi. Quantum copy-protection based on holographic data storage, BUTE, Faculty of Electrical Engineering and Informatics, Department of Telecommunications, 2008.
21. Laszlo Gyongyosi. Quantum Computation in computer network attacking, BUTE, Department of Measurement and Information Systems, Search-Lab, 2007.
22. Laszlo Gyongyosi. The holographic quantum copy-protection protocol, BUTE, Faculty of Electrical Engineering and Informatics, Scientific Students Association, 2007, Special award of the Scientific Students Association, BUTE
23. Laszlo Gyongyosi. A technical breakthrough in prime factorization, BUTE, Faculty of Electrical Engineering and Informatics, Scientific Students Association, 2007, Special award of the Scientific Students Association, BUTE
24. Laszlo Gyongyosi. Simulation of the perfect quantum based key agreement, National Scientific Students Association, (OTDK 2007), Award of the Hungarian Scientific Students Association of Computer Science and Information Technology
25. Laszlo Gyongyosi. Simulation of the perfect quantum based key agreement, BUTE, Faculty of Electrical Engineering and Informatics, Scientific Students Association, 2006, 1st prize.
26. Laszlo Gyongyosi. Formal Analysis of Quantum Cryptography, BUTE, Faculty of Electrical Engineering and Informatics, Scientific Students Association, 2006, 3rd prize.
Conference Organizing
QuantumComm 2012 - The Improving Quantum World
2nd International ICST Conference on Quantum Communication and Quantum Networking (QC2012)
Budapest, Hungary, March 19, 2012 – March 22, 2012.
(Co-organized by the Budapest University of Technology, Department of Telecommunications in cooperation with Universita' di Pavia, Foundations of Quantum Mechanics, and Quantum Optics, Qubit.it).
webpage: http://www.quantumcomm.org/
Teachning activity
Quantum Computing and Communications
Measuring Laboratory (Informatics and Electrical Engineering)
Awards
PhD Student Grant of Optical Society of America (OSA), University of Arizona, USA.
BUTE PhD Researcher Fellowship 2010, Budapest University of Technology and Economics.
"SANDOR CSIBI" PhD Researcher Scholarship 2010, Pro Progressio, Faculty of Electrical Engineering and Informatics, Budapest University of Technology and Economics.
BEST PAPER AWARD 2010, International Conference on Computer Engineering and Applications, Harvard University, Cambridge, USA.
BEST PAPER AWARD 2009, FUTURE COMPUTING, The First International Conference on Future Computational Technologies and Applications, 2009.
BEST PAPER AWARD 2009 - "POLLAK-VIRAG" - from the Scientific Association for Infocommunication (Hungary)
Republican Scholarship
Professional Scholarship, Faculty of Electrical Engineering and Informatics, BUTE (A-level, highest category)
University Professional Scholarship, BUTE (A-level, highest category) .
Short C.V.
Laszlo Gyongyosi received the M.Sc. degree in Computer Science with Honors from the Budapest University of Technology and Economics (BUTE) in 2008. He is a final year Ph.D. Candidate at the Department of Telecommunications, BUTE. His research interests are in Quantum Computation and Communication, Quantum Channel Capacity, Quantum Cryptography and Quantum Information Theory. He is currently completing a book on advanced quantum communications, and he teaches courses in Quantum Computation. In 2009, he received Future Computing Best Paper Award on quantum information, in 2010, he was awarded the Best Paper Prize of University of Harvard, USA. In 2010, he obtained a Ph.D. Researcher Grant from University of Arizona, USA.
