Doctoral School of Mathematics and Computer Science 

Department of Stochastics/Institute of Mathematics

Supervisor: Domokos Szász

Asymptotic behavior of mathematical billiards and random walks 

Introducing the research area

In this research, I investigate mathematical billiards - mainly Sinai billiards or dispersing billiards-, and some random walk models. Sinai billiard is a chaotic dynamical system (hyperbolic, ergodic, mixing, Bernoulli), thus in some sense it behaves as though it was random. In the last decades, after an immense progression of the theory - in such model of Newtonian mechanics - it has become possible to derive some laws of statistical physics in a mathematically rigorous way.

 

Brief introduction of the research place

My research work is carried out at the Department of Stochastics, Mathematical Institute. There is a group of researchers affiliated at the Department of Stochastics and the Department of Differential Equations mainly consisting of professor Domokos Szász (vice president of the Hungarian Academy of Sciences) and his students. The successful seminars, Stochastics Seminar and Dynamical Systems Seminar, indicate the prestigious position of the research place.

History and context of the research

Billiard

The definition of the Sinai billiard is pretty simple. On the d dimensional torus (typically d=2), there are finitely many strictly convex disjoint sets with smooth boundary which are called scatterers. A massless particle moves freely on the complement of the scatterers until it hits the boundary of one of them, when it is simply reflected (with the angle of reflection being equal to the angle of incidence) (Figure 1). The periodic Lorentz process is defined the same way on the periodically extended scatterer configuration in the d dimensional space (Figure 2).

 

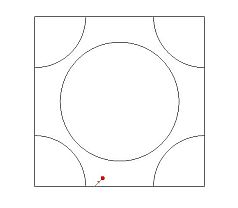
Figure 1 : A planar Sinai billiard table                  Figure 2: a trajectory of 15 collisions in a

with finite horizon. Animated version.                Lorentz process with infinite horizon

 

Brownian motion

Roughly speaking, the Brownian motion is the motion of a dust particle in a glass of water. Since the dust particle is bombarded by a vast number of molecules from different directions, the resulting movement is irregular, random. On the other hand, mathematicians often use the expressions Brownian motion and Wiener process (Figure 3) equivalently. The latter is a mathematical model for Brownian motion, a so-called stochastic process.

 

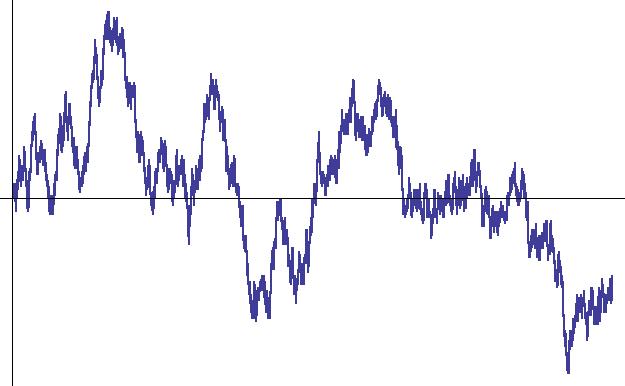
Figure 3: a realization of a one dimensional Wiener process

(here, the horizontal axis is time)

 

Hence in the dynamical theory of Brownian motion, every result proving the presence of the Wiener process in some deterministic Newtonian system, e.g. in Sinai billiard, is of crucial importance. The first results in these direction were [BS80] and [BSCh91]. While the state of the art result ([ChD09b]) also includes two interacting particles. Besides, nowadays one has real chance to discuss other phenomena from statistical physics (e.g. relaxation [Y98], thermal conductivity [GG08]).

Aims of the research

My aim is to understand and prove stochastic properties of billiard models.

From this point of view one can distinguish two essentially different scatterer configurations: in the case of finite horizon, the free flight of the particle is bounded (as in Figure 1), while in infinite horizon it is unbounded. In the latter case, one can find an infinite line which is disjoint to all of the scatterers, see Figure 2.

In order to observe the previously mentioned convergence to the Wiener process (which statement is also called the invariance principle) one needs to use diffusive scaling in the case of finite horizon, i.e. to rescale the trajectory of length n by . In the case of infinite horizon, the scaling is superdiffusive, that is  should be replaced by  [SzV07, ChD09a].

The related questions we are interested in are the following.

 

1. If one modifies the scatterer configuration in a bounded region, does the invariance principle remain true? To answer this question, it is useful to investigate the recurrence properties of the particle to a finite set (how much time does it take to come back, how much time is spent there, when does it hit this finite set if starts from far away, etc.). Such questions are dealt with in [DSzV08] and [DSzV09] in finite horizon; can these results be generalized to infinite horizon?
2. What happens if instead of the previous local perturbation, one considers some other inhomogeneity - even time dependent scatterer configuration?
3. How many scatterers are visited by the particle up to time n if n is large?
4. In all the above questions we would like to know whether the particle’s behavior resembles to the one of the appropriate analogous random walker.

 

Methodology

As is was already noted, the subject of our research are random walks and Lorentz processes.

A random walk by definition is the random process in which a particle is wandering on the d dimensional lattice in discrete time. The steps are always assumed to be independent of the current position. Sometimes they are also independent of each other - this is called a simple walk. Here, of the non simple walks, we only treat the so called random walks with internal states. In this model, the distribution of steps are governed by an internal state (an element of a finite set, see Figure 4).

 

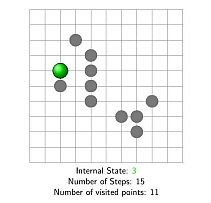
Figure 4: visited points by a random walk with internal

in the first 15 steps. Animated version.

 

In the asymptotic analysis of random walks, a basic tool is the Fourier transform which is also called characteristic function. The essence of this method is as follows. Let  X, X1, X2, … be random variables (i.e. “random numbers”). Their characteristic functions are some functions  defined by

,

where E denotes expectation, and i is imaginary unit. A nice property of the functions u is that Xn converges weakly to X (i.e. has approximately the same distribution) if and only if the functions un(t) converge to u(t). This, together with the fact that the characteristic function of a sum of independent random variables is the product of the individual characteristic functions, makes the computation of some limit distributions easy in the independent case. This method has deep generalizations. A simple one allows us to prove local limit theorems, i.e. we can approximate the probability that a random walker arrives back at the origin after many steps, whence we can analyses recurrence properties. A much deeper generalization renders the method suitable for random walk with internal states; in this case the Fourier transform is matrix valued. Finally, by introducing a one parameter family of operators acting on some function spaces, one can use the method even in the case of some deterministic systems.

 

In the case of Sinai billiard, it is usual to introduce a Poincaré section, i.e. to consider the dynamics only at the time instants of collisions. This way one obtains a two-dimensional phase space: one parameter is the position on the boundary of some scatterer, the other describes the velocity. A nice property of the discrete billiard map is the hyperbolicity (caused by the convexity of the scatterers) which means that the image of two nearby points are getting exponentially farther from each other in the course of iterations. On the other hand, grazing collisions imply the existence of singularities, which is an awkward property. Due to the hyperbolicity, there exist stable and unstable manifolds. An unstable manifold is expanded by the dynamics (hyperbolicity) and torn by the singularities (see Figure 5). The essence of the method of Chernov and Dolgopyat ([ChD09b], [Ch06]) is that in the so called growth lemma, they prove that the expansion predominates over fragmentation and then by coupling some measures on unstable manifolds, they can prove exponential decay of correlation and invariance principle (coupling lemma).

 

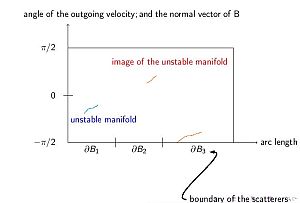
Figure 5: The phase space of a Sinai billiard; the image of an unstable manifold

is the union of some unstable manifolds

 

Results

1. In connection with our first question concerning the local perturbation of the planar Lorentz process with infinite horizon, we consider the analogous simple random walk model. Here, the probability of a step of length n is roug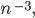hly , [N11b]. All the relevant recurrence properties are proven. The result says that it is more difficult for the walker to return in this model than in the case of finite horizon. Namely, the probability of the event that it does not return until time n is roughly 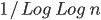, while in the case of finite horizon this is just . Similarly, the other recurrence properties are also quite different. In the proof we apply the Fourier transform to prove some local limit theorem.
2. For other types of inhomogeneities, we mention two articles: [NSz12], [NSzV12]. In the first one, we consider a periodic Lorentz process in an infinite horizontal tube with an extra vertical wall at a fix position (at the origin, say). There is a tiny hole on the wall, through which the particle can cross the wall. Thus the scatterer configuration is not periodic, and we even allow the size of the hole to change in time, yielding time inhomogeneity. If there is no hole at all, the scaling limit of the trajectory is the reflected Wiener process (Figure 6), while if it is of fixed positive size, the limit is just the Wiener process. In the general case (in finite horizon, under some further conditions) we prove that the diffusively scaled limit is the so called quasi reflected Wiener process (Figure 7) which is hence a joint generalization of both Wiener process and reflected Wiener process. The interesting case, i.e. when the limit is indeed quasi reflected, is when the size of the hole at time n is approximately 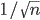. In the paper [NSzV12], we prove convergence to the set of normal distributions for some observables under general time inhomogeneity, but this method is only valid for one dimensional dynamics (thus not for billiards). In the proof, we use the popular method of martingale approximation.

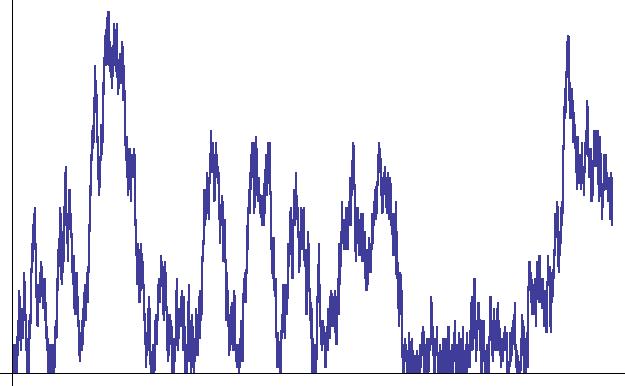
Figure 6: reflected Wiener process - with the realization of Figure 3.

 

Figure 7: quasi reflected  Wiener process - with a realization of Figure 3.

 

1. Finally, in [N11a], we consider the number of distinct sites visited by a random walk with internal states. This problem for simple symmetric random walk was treated in [DE51], and for planar Lorentz process with finite horizon in [P09]. We generalize all the statements of [DE51] and even include the one dimensional case. The most interesting part of the results is the following. In two dimensions, the number of visited sites until time n is about 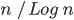, while in dimension , this is some constant times n. This is connected to the fact, that the random walk in dimensions up to two returns to its starting position with probability one, while in dimension  with positive probability it never returns.

 

Expected impact and further research

In the mathematical theory of Lorentz processes with infinite horizon in high dimensions almost nothing is proven. At the moment, together with Domokos Szász and Tamás Varjú, we are working on distinguishing the diffusive and superdiffusive scatterer configurations. The conjecture - which was investigated by physicists, too - is that superdiffusion only appears in the case, when there is some affine subspace of maximal dimension, which is disjoint to the scatterers ([ZGNR86], [D12]). We want to prove the first two conjectures of Dettmann [D12].

We also plan to give a new proof (with the growth lemma and the martingale method) for the invariance principle in the case of planar infinite horizon. This might be useful for the treatment of local perturbations in the future.

 

Publications, references, links

Publications

 

[N11a] Nándori, P., Number of distinct sites visited by a random walk with internal states, Probability Theory and Related Fields 150 3 (2011), 373-403.

 

[N11b] Nándori, P., Recurrence properties of a special type of Heavy-Tailed Random Walk, Journal of Statistical Physics, 142, 2 (2011), 342-355.

 

[NSz12] Nándori, P., Szász, D., Lorentz Process with shrinking holes in a wall

Chaos: An Interdisciplinary Journal of Nonlinear Science 22, 2, 026115 (2012).

 

[NSzV12] Nándori, P., Szász, D., Varjú, T., A central limit theorem for time-dependent dynamical systems, Journal of Statistical Physics, 146, 6 (2012), 1213-1220.

 

Links

 

Scholarpedia article on mathematical billiards

Krámli András: The chaos from the viewpoint of a mathematician, Természet Világa 135, 7 (2004), ( in Hungarian)

Review paper on hyperbolic billiards by Chernov and Dolgopyat from the International Congress of Mathematicians, 2006

 

References

 

[BS80] Bunimovich L. A., Sinai, Ya. G., Statistical properties of Lorentz gas with

periodic configuration of scatterers, Comm. Math. Phys. 78 (1980/81), 479-

497.

[BSCh91] Bunimovich L. A., Sinai, Ya. G., Chernov, N. I., Statistical properties of two-

dimensional hyperbolic billiards, Russ. Math. Surveys 46 (1991), 47-106.

 

[Ch06] Chernov, N., Advanced statistical properties of dispersing billiards, Journal of Statistical Physics 122 (2006), 1061-1094.

 

[ChD09a] Chernov, N.,  Dolgopyat, D., Anomalous current in periodic Lorentz gases with infinite horizon, Russian Mathematical Surveys 64 4 (2009), 651-699.

 

[ChD09b] Chernov, N., Dolgopyat. D., Brownian Brownian Motion–1, Memoirs AMS. 198, No. 927 (2009), pp 193.

 

[D12] Dettmann, C., New horizons in multidimensional diffusion: The Lorentz gas and the Riemann Hypothesis, Journal of Statistical Physics 146 (2012) 181-204.

 

[DSzV08] Dolgopyat, D., Szász, D., Varjú, T., Recurrence Properties of Planar Lorentz Process, Duke Mathematical Journal  142 (2008), 241-281.

 

[DSzV09] Dolgopyat, D., Szász, D., Varjú, T., Limit Theorems for Perturbed Lorentz Processes. Duke Mathematical Journal 148 (2009), 459-499.

 

[DE51] Dvoretzky, A., Erdős, P., Some Problems on Random Walk in Space, Proc. 2nd Berkeley Sympos. Math. Statis. Probab. (1951), 353-367.

 

[GG08] Gaspard, T., Gilbert, T., Heat conduction and Fourier's law in a class of many particle dispersing billiards, New Journal of Physics 10 103004 (2008).

 

[P09] Péne, F., Asymptotic of the number of obstacles visited by a planar Lorentz process, Discrete and Continuous Dynamical Systems, series A, 24 (2009), 567-588.

 

[S70]  Sinai, Ya. G., Dynamical systems with elastic reflections: Ergodic properties of

dispersing billiards, Russ. Math. Surv. 25 (1970), 137–189.

 

[SzV07] Szász, D., Varjú, T., Limit Laws and Recurrence for the Planar Lorentz Process with Infinite Horizon, Journal of Statistical Physics 129 (2007), 59-80.

 

[Y98] Young L.–S. Statistical properties of dynamical systems with some hyperbolicity, Annals of Mathematics 147 (1998), 585–650.

 

[ZGNR86] Zacherl A., Geisel T., Nierwetberg, J., Radons, G., Power spectra for anomalous diffusion in the extended Sinai billiard, Physical Letters 114A (1986) 317-321.