BME Pál Vásárhelyi Doctoral School in Civil Engineering and Earth Sciences  

BME Department of Construction Materials and Engineering Geology

Supervisor: Dr. István  Zsigovics  

Constitutive modeling of rebound surface hardness of concrete –
A sixty-year-old question answered 

 

Introducing the research area

Reinforced concrete is a structural material most widely used in the built human environment and – due to its durability – a particularly important end product of the sustainable construction.

 

 

Fig. 1: Application of concrete in the construction industry

 

Compressive strength of concrete is the most important input data for engineering calculations during the design of reinforced concrete structures. Compressive strength of concrete can be determined by testing the molded specimens or by core specimens drilled from existing structures with loading up to failure.

 

Fig. 2: Process of compressive strength test of concrete

 

Concerns about laboratory compression tests are:

1) Molded specimens do not always represent the actual condition of structural concrete.

2) Drilling the core specimens from certain structural members is not always possible (due to the risk of loss of structural stability or poor accessibility of the structural element to be examined).

Non-destructive testing (NDT) devices can theoretically provide solutions for both concerns.

The most successful strength estimation methods involve principles, which make the direct or indirect consequences of the factors determining the compressive strength measurable or (in some cases) provide strength estimation by moderately destructive in-situ measurements. These methods include the subject of present research work: a classic NDT method based on the surface hardness testing of concrete which became popular in the construction industry during the 1950s.

Brief introduction of the research place

The Department of Construction Materials and Engineering Geology (BME Faculty of Civil Engineering) mainly engaged in the education and research of structural material properties. Our department gives lectures and laboratory sessions for five faculties of BME, and through running the largest laboratory in the Faculty of Civil Engineering it significantly contributes to a better understanding of material properties. In our scientific work we keep focusing on the importance of the synergistic link of theoretical and laboratory research, which is of particular importance in material sciences. The laboratory has an accredited status in more than 50 fields. The Head of the Department, Prof. György L. Balázs was elected the President of the fib (International Federation for Structural Concrete) in May 2010 – a federation with more than a half century of history and comprising 5 continents and 42 member countries. 

History and context of the research

Surface hardness testing is a long established NDT method for the strength estimation of construction materials and goes back several hundred years. Hardness testing was the first material testing attempt in the engineering activities during the 1600s, long before the development of the systematic material experiments carried out in laboratories. Theoretical hardness research was initialized by the pioneering work of Heinrich Hertz in contact mechanics during the 1880’s. As a result, a variety of plastic indentation hardness testing methods (Brinell, Vickers, Knoop etc.) were developed, which have been used in several fields also for in-situ measurements up to present day. Unlike these methods, surface hardness testing of concrete uses the rebound principle. The testing device (known as Schmidt-hammer in Hungary after the inventor) developed in 1950 can be operated very simply, which contributed to its rapid spread. Today, the rebound hammer is the most popular in-situ testing device for concrete strength estimation.

 

 

Fig. 3: Use and structure of the Schmidt hammer

 

In the Schmidt rebound hammer a spring accelerated mass is sliding along a guide bar and impacts one end of a steel plunger of which far end is compressed against the concrete surface. The measure of the hardness is the rebound index (R): the ratio of paths driven by the hammer mass during rebound (xr) and before impact (x0). R = xr/x0 × 100.

It should be emphasized that the rebound hammer gives a measure of surface hardness (the rebound index) that can be apparently related to the needed parameter (compressive strength of concrete) only empirically. The technical literature of the topic is very rich, however, after surveying several hundreds of papers and studies published in the last more than 60 years it can be concluded that the theoretical background of the relationship between compressive strength and rebound hardness of concrete is not available and the remarkable diversity of the numerous proposals needs to be analyzed and explained. (This diversity is partly understandable, since concrete is macroscopically a heterogeneous, multiphase material with capillary porous system and time dependent properties.)

 

 

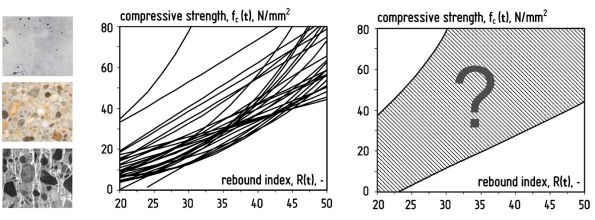
Fig. 4: Rebound surface hardness vs. compressive strength relationships from the technical literature

 

The research goal, open questions

It can be observed in the technical literature that the assumed direct relationship between compressive strength and rebound index tends to be given as the regression curve of a heteroscedastic (i.e. increasing standard deviation in strength (Y variable) for increasing rebound index (X variable)) data set. In many cases, these functions are developed by linear regression, while the linear regression should be strictly applied only for homoscedastic data fields (i.e. constant standard deviation of the dependent variable).  Such representation of the relationship between compressive strength and rebound index is questionable in many respects, as no causal connection exists between the independent and the dependent variables. Both properties are results of the same influencing parameters.

 

 

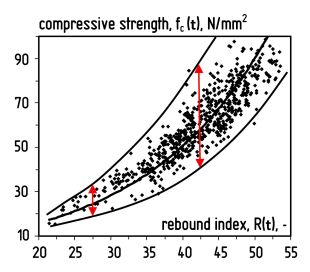
Fig. 5: Apparent heteroscedastic relationship of fc(t) – R(t)

 

It is empirical evidence that the standard deviation of concrete compressive strength depends on the quality of concreting work, and does not depend on the average compressive strength. That is, the magnitude of standard deviation in strength of concretes of different compressive strengths and prepared with the same care is expected to be equal.

If a direct relationship is assumed between compressive strength and rebound index, the observation of heteroscedastic data set cannot be accounted for the standard deviation of the strength. Furthermore, considering that in practice the quality control in the manufacture of higher strength concretes is typically stricter than for lower strength concretes, then one can not expect the standard deviation of the strength to increase, but on the contrary, to decrease.

It is also an empirical evidence that there is a relationship between the surface hardness and carbonation depth (the maximum depth where the CO2 content of the air diffuses into the capillary pores of concrete and turns part of the portlandite into limestone causing a decrease of the pH value to 8.3) of concrete: the development of the carbonation results higher surface hardness. The gas permeability of the lower strength concretes is higher (greater carbonation depth) while the gas permeability of the higher strength concretes is lower (smaller carbonation depth), during the same period of time. Considering the above, the representation of measured values as data points of the same population would logically predict the formation of a data field with an appearance opposite to the heteroscedastic one.

According to the initial hypothesis of my PhD research work, a system of relationships should exist between the compressive strength and rebound index of concrete, which highlights that the formulation of a direct relationship between the two properties is impossible, but an unambiguous series of functions can be generated by careful selection of influencing parameter(s), which can follow the empirical observations with sufficient accuracy and also explain the observed anomalies. The hypothesis assumed that the influencing factor(s) is/are related to the degree of hydration of the hardened cement paste.

Methodology

Deductive principles were followed in the first, theoretical part of my research work. My train of thought was based on theoretical considerations whenever it was appropriate, while in other cases empirical relationships were studied. General observations and theoretical models were examined considering the compressive strength and rebound index. Models were chosen where degree of hydration was found to be the primary driver of phenomena.

Since the mathematical modeling and experimental determination of the degree of hydration do not satisfy the principle of “intended simplicity for the practical use”, therefore a simplification was introduced; the degree of hydration was characterized by three variables: type of cement, water-cement ratio (w/c) and the age of concrete. During the theoretical research work, the randomness of the phenomena were not taken into consideration by focusing on the general laws, that is, the particular influencing parameters were not considered as random variables. Revealing the possible internal links has lead to the hypothesis of a constitutive model between the compressive strength and rebound index of concrete which was able to generate data points of compressive strength and rebound index for concretes made from a given type of cement, with a given water-cement ratio, at a given age, by means of five general relationships. The generator functions are (all of them can be validated empirically): relationship between the water-cement ration and compressive strength of concrete at the age of 28 days; development of compressive strength in time; relationship between compressive strength and rebound index of concrete at the age of 28 days; development of carbonation depth in time; relationship between carbonation depth and rebound index of concrete.

 

 

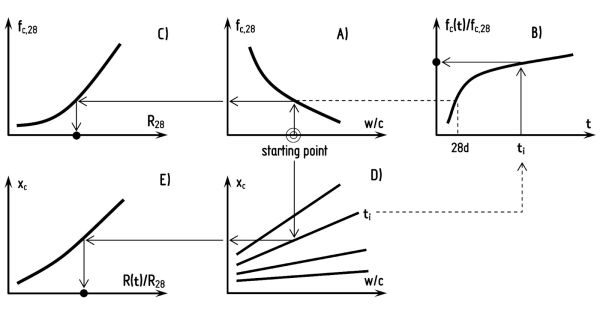
Fig. 6: The generation scheme of the model (5 functions)

 

The applicability of the model was verified by parametric simulation: with the preliminary selection of arbitrary function parameters a series of functions were generated that could simulate results that are similar to the real observations.

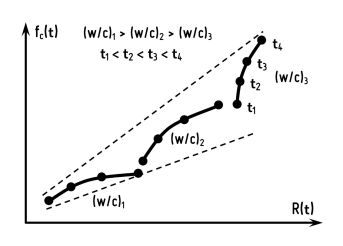
Fig. 7: Typical schematic fc(t) vs. R(t) response as an output of the model: a set of curves corresponding to different water-cement ratios at different ages of the concrete

 

The intention of the second, experimental part of the research work was to verify the real applicability of the hypothesized constitutive model. Inductive principles were followed, i.e. laboratory tests were carried out under strictly controlled experimental conditions, with the introduction of sufficiently large number of test parameters changed on a wide range, on a large number of specimens with double repetitions. The general behavior of the hypothesized constitutive model was detected by the appropriate graphical representation of  the particular observations.

Results

The number of the experimental parameters was gradually increased in the consecutive test series during the laboratory tests , involving more and more factors in the analysis.

Tests were carried out with altogether eight types of cement. The verification test series shown here (which included the most experimental parameters) was a 7-parameter experimental study, with 864 specimens (150 mm concrete cubes). The variable parameters of the study were water-cement ratio, type of cement, cement content, mixing water content, cement paste content, aggregate-cement ratio and testing age. The type of aggregate (Danube sand and gravel), the design air content of the compacted fresh concretes (1.0 V%), the consistency of the tested concrete mixes (500±20 mm flow, adjusted with superplasticizer admixtures), the mode of compaction (in steel formwork on a vibrating table) and the mode of curing and storing (7 days under water, then storage under laboratory conditions, i.e. 20±3°C temperature and 65±5% relative humidity) were the same apart from the variable parameters.

 

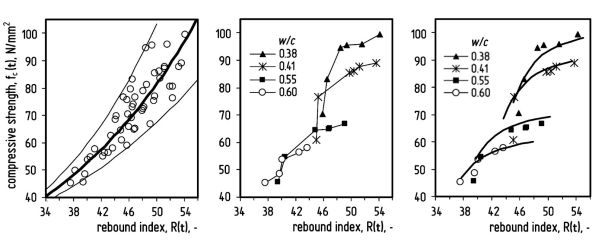
Fig. 8: Experimental verification of the model on concrete cube specimens prepared with CEM I 42.5 N portland cement: data in non-separated representation; data separated by the applied water-cement ratios; data represented together with the fitted model

 

By the use of the model the rebound surface hardness of concrete can be understood. The applicability of the model was verified for numerous types of cement, on a wide range of water-cement ratio, at several ages of concrete.

The model not only clarifies several questions yet in its present form that remained unclear during the past 60 years, but allows further development in the future due to its transparent structure.

Although the constitutive model outlined the influencing parameters determining the rebound surface hardness of concrete, it was a further question which mechanical property has the strongest correlation with the hardness values of different dynamic hardness testing devices (L- and N-type of Schmidt hammers, Leeb scleroscope) and the Brinell hardness. During the experimental studies (covering a wide range of compressive strength and several ages of concrete) the hypothesis was proved that the amount of energy introduced during testing determines the surface hardness related property through the obtained hardness measure. In hardness tests resulting in low amount of dissipated energy (e.g. Leeb hardness test on any strength of concrete or Schmidt rebound hardness test on high strength concrete) hardness measure can be correlated to the Young’s modulus. In hardness tests resulting in high amount of dissipated energy (e.g. Brinell hardness test on any strength of concrete) the hardness measure can be correlated to the compressive strength. In the case of intermediate amount of dissipated energy the effect is not obvious. Experimental results highlight that in practice the devices most widely used for strength estimation (Schmidt hammers) have strict limits of application.

Expected impact and further research

Results of the series of laboratory tests verified the hypothesis about the existence of the constitutive model between the compressive strength and rebound index. An essential question was revealed and answered in this field which has not been clarified for sixty years. The model recognizes a possible theoretical relationship between the two time dependent properties.  The transparency of the model provides the potential of further theoretical as well as practical developments on a wide range. Results published in international referred journals in 2011-2012 were welcome and received independent citations. Future aim of my research is to extend the model into a probability theory direction to become more usable for the practice.

 

Publications

 

[1]        Szilágyi K. – Borosnyói A. – Zsigovics I. (2012) "Understanding the rebound surface hardness of concrete", Journal of Civil Engineering and Management, accepted for publication

[2]        Szilágyi K. (2012) "„Hardness studies on porous solids", Conference of Junior Researchers in Civil Engineering, Budapest, June 19-20, 2012, pp. 240-247, in press

[3]        Szilágyi K. – Borosnyói A. – Gyurkó Z. (2012) "Hardness testing of porous solids", Engineering Geology-Rock Mechanics Conference 201, Budapest, January 26, 2012, pp. 297-312, in Hungarian

[4]        Szilágyi K. – Borosnyói A. – Zsigovics I. (2011) "Rebound surface hardness of concrete: Introduction of an empirical constitutive model", Construction and Building Materials, Vol. 25:(5), May 2011, pp. 2480-2487, doi:10.1016/j.conbuildmat.2010.11.070

[5]        Szilágyi, K. – Borosnyói A. - Zsigovics I. (2011) "Surface hardness and related properties of concrete", Concrete Structures, Vol. 12, 2010, pp. 51-57

[6]        Szilágyi, K. – Borosnyói A. – Dobó K. (2011) "Static indentation hardness testing of concrete: a long established method revived", Építőanyag, Vol. 63. (1-2), 2011, pp. 2-8

[7]        Szilágyi, K. – Borosnyói A. - Zsigovics I. (2010) "Introduction of a constitutive model for the rebound surface hardness of concrete", Concrete Structures, Vol. 11., 2010, pp. 46-52

[8]        Borosnyói A. - Szilágyi K. (2010) "About the Hungarian regulation of the Schmidt hammer test of concrete", Beton, Vol. XVIII. No. 1. 2010/1, pp. 14-16, in Hungarian

[9]        Szilágyi, K. – Borosnyói A. (2009) "50 years of experience with the Schmidt rebound hammer", Concrete Structures, Vol. 10., 2009, pp. 46-56

[10]        Szilágyi K. – Borosnyói A. (2008) "50 years of the Schmidt hammer: Past, present, future. 1. part: Methods and literature review", Vasbetonépítés, Vol. X. No. 1. 2008/1, pp. 10-17, in Hungarian

[11]        Szilágyi K. – Borosnyói A. (2008) "50 years of the Schmidt hammer: Past, present, future. 2. part: The European standardization and its Hungarian significance", Vasbetonépítés, Vol. X. No. 2. 2008/2, pp. 48-54, in Hungarian

[12]        Szilágyi K. – Borosnyói A. (2008) "50 years of the Schmidt hammer: Past, present, future. 3. part: Scientific considerations and outlook", Vasbetonépítés, Vol. X. No. 3. 2008/3, pp. 73-82, in Hungarian

[13]        Szilágyi K. (2008) "Non-destructive testing of concrete strength", BME PhD Symposium in Civil Engineering, Budapest, Hungary, November 28, 2008, in press

 

Contributions at Student’s Scientific Workshop at BME Faculty of Civil Engineering (as supervisor):

[1]        Gyurkó Z. (2011) "Analyses of the relationships between surface hardness and strength related properties", BME, November 16, 2011, III. prize in the faculty, nomination to the National Student’s scientific workshop (to be organized), in Hungarian

[2]        Dobó K. (2010) "Surface hardness testing of concrete by static and dynamic methods", BME, November 17, 2010, II. prize in the faculty, III. prize at National Student’s scientific workshop, in Hungarian