 |
BMe Research Grant |

|
Vásárhelyi Pál Doctoral School
Faculty of Civil Engineering, Department of Structural Engineering
Supervisor: László Gergely Vigh PhD.
Buckling Restrained Braced Frame design procedure evaluation through experimental and numerical analyses
Introducing the research area
My research focuses on the behaviour of Buckling Restrained Braces (BRB). The primary objective is to verify that the design procedure proposed by our research group is appropriate for European application and its use results in economical earthquake resistant Buckling Restrained Braced Frames. A special framework for evaluation of the design of anti-seismic systems is adopted to achieve this goal. The framework is configured with the help of experimental and numerical analysis results.


Figure 1. Buckling Restrained Braced Frames (source: Star Seismic)
Brief introduction of the research place
I carry out my research at the Department of Structural Engineering. Our department has been actively participating in state-of-the-art research in the field of Structural Engineering and Bridge Design. We are also members of several high priority projects as consultant, co-designer or independent inspector (e.g. Pentele bridge, Hárosi bridge). Experiments performed at our accredited Structural Laboratory provide valuable information on structural behaviour.
Earthquakes and earthquake resistant design became one of the main research interests in the department during the past decade. Currently a research group is devoted to this subject. László Gergely Vigh, the leader of the group is also a member of the TC13 committee of ECCS, thus actively participates in the improvement of the European seismic design standard (Eurocode 8 [1]).
History and context of the research
Earthquake engineers have recognised the inefficiency of conventional, elastic structural design at regions of high seismicity by the second half of the 20th century. When subjected to loading, linearly elastic structural members suffer deformations that are proportional to the load intensity. These deformations are only temporary; the members regain their original shape after unloading. Dissipative structural members are typically characterized by plastic behaviour beyond a certain load level. Plastic deformations are irreversible, they remain as residual deformations even after unloading. An important consequence of plastic behaviour is the significant amount of dissipated energy through plastic deformations.
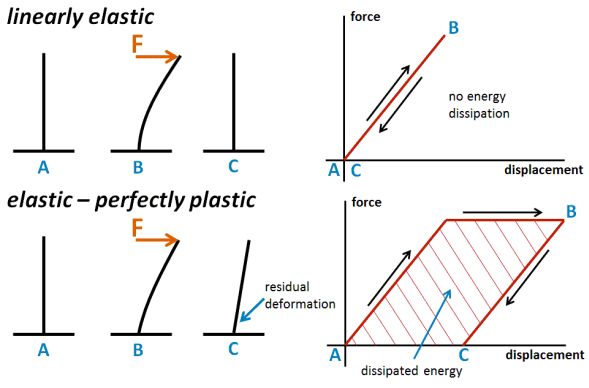
Figure 2. Comparison of the behaviour of linearly elastic and dissipative structural members
Provided that there are dissipative members designed at key points in a structure, it will be able to dissipate the majority of seismic energy and significantly reduce the internal forces resulting from earthquakes. Design of such structures is a complex procedure (capacity design) that was established by Tamás Paulay.
Structural steel is frequently used in dissipative structural members because of its advantageous inelastic behaviour. However, capacity of conventional steel members is significantly limited under compression, because they typically buckle before reaching the load level that corresponds to plastic behaviour. Consequently, these members are taken into account in design as tension-only braces and not used to their full capacity. Buckling Restrained Braces were developed in the 1980s in Japan [2] to improve steel brace performance by preventing the occurrence of buckling. Figure 4 displays the components of the element. A central steel core is continuously supported by a concrete-filled steel hollow section. The continuous lateral support prevents buckling of the core. The core and the casing are decoupled, so that axial loads are resisted by the steel core only. BRB elements are capable of producing the theoretical steel material behaviour at an element level, thus their energy dissipation capability is superior to conventional steel braces.
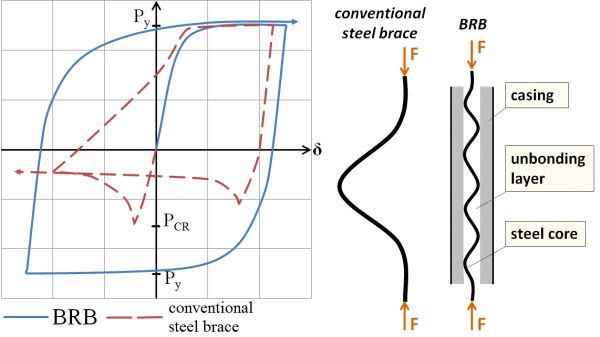
Figure 3. Comparison of cyclic behaviour of conventional steel braces and the BRB
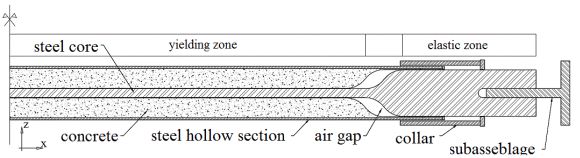
Figure 4. Primary components of a buckling restrained brace
The research goal, open questions
BRBs have been actively used and researched in both Japan and the United States by the year 2000 [3,4]. Their investigation in Europe began at the end of the last decade, while practical use is hindered by the lack of a standardized European design procedure. Our primary objective is the evaluation of a design procedure based on the principles of capacity design that can be included in the next revision of the European seismic design standard. The proposed procedure shall be simple enough to be applicable as a part of everyday engineering practice.
The performed research shall analyse the introduced simplifications to BRB design and verify the appropriate behaviour of structures designed with the proposed procedure. This requires detailed and accurate understanding of BRB behaviour, especially its energy dissipation capability under cyclic loading and its expected failure modes. Although there are experimental results in the literature (e.g. [5,6]), they do not fully answer to some of our questions. BRB failure because of low cycle fatigue and the resulting dependence of BRB performance on the load history for instance is generally accepted, but there are only a limited number of results in literature concerning this phenomenon. Collecting more experimental data on this topic promises more accurate estimation of the capacity of BRB-based structural solutions.
Besides facilitating the application of BRB frames in Europe, our results also lead to a more detailed understanding of BRB behaviour, thus they are also applicable to research outside of Europe. Our research group cooperates with one of the world’s leading BRB manufacturers, Star Seismic, and we established joint research projects with several European universities.
Methodology
Investigation of BRB behaviour
BRB behaviour under cyclic loading has been investigated by uni-axial cyclic load tests on a total of 10 specimens. A custom loading frame has been built at the Structural Laboratory for these experiments.
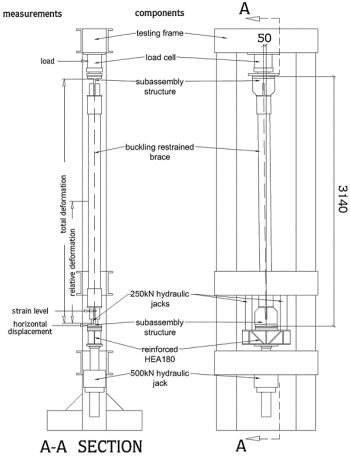

Figure 5. Custom loading frame designed for the experiments
Three load protocols (load history functions) have been developed that comply with the requirements of EN15129 [7], the European standard for anti-seismic devices. Each protocol focuses on a specific BRB property (e.g. energy dissipation capability, load history influence). Loading was displacement controlled in all cases; the prescribed displacement levels were reached by applying load on the BRB specimen through hydraulic jacks in the loading frame.
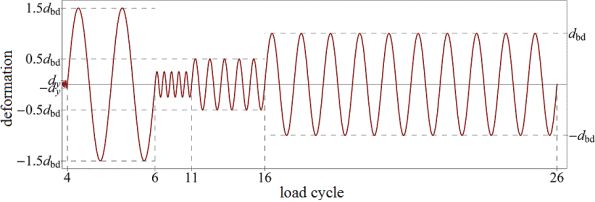
Figure 6. Load protocol for the analysis of load history influence - the initial cycles with large amplitude are expected to affect the behaviour in later cycles
The experienced behaviour is best described by force-displacement diagrams. The diagram in Figure 7 shows the initial elastic behaviour, followed by the yielding of the steel core. The effect of the two types of hardening (kinematic and isotropic) is also visible on the curves. Note that BRB behaviour is asymmetric; the elements have increased capacity under compression.
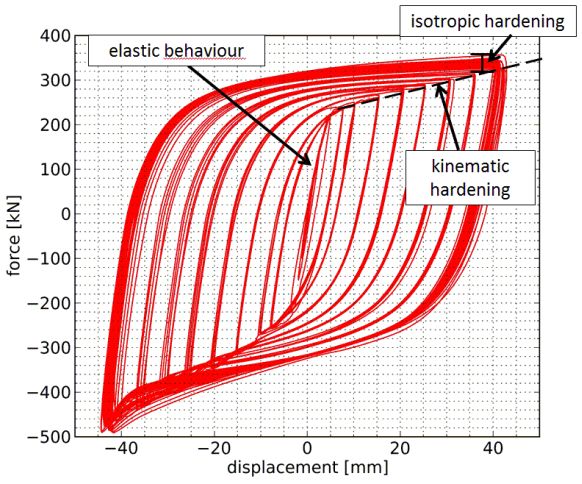
Figure 7. Typical experimental force-displacement diagram
Numerical BRB model
Laboratory experiments require significant financial resources and time, therefore virtual experiments are often used in current civil engineering research projects. These are experiments performed on computer models (typically in a finite element modelling environment) calibrated by the available results from laboratory tests. Our research group has such a model for BRB that provides deeper understanding to element behaviour [Z1, 8].
Virtual experiments require a detailed model made of three dimensional finite elements that follow the geometry of the specimen and the changes in material properties with high accuracy. This complex model is an effective tool for simulated experiments, but it is inefficient for the global analysis of frame structures, because it uses a the large amount of computational resources. Global analysis requires a simplified, faster model that still approximates BRB behaviour with sufficient accuracy. I developed this simple model by using a simple prismatic beam element with a custom made material model [Z2]. Since element geometry cannot be followed by such a simple finite element, all BRB characteristics had to be modelled by the custom material.
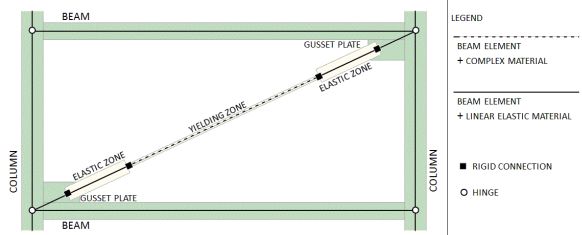
Figure 8. Configuration of the simplified numerical BRB model
Design procedure evaluation
The proposed design procedure is verified with a framework based on recommendations in the FEMA P695 document [9]. The suggested methodology evaluates design procedure through the investigation of a large number (30-50) of typical structures, so-called archetypes. These are buildings that are expected to use the proposed system in the region under consideration (Europe in our case). Performance of each archetype is evaluated by detailed nonlinear dynamic analysis [10].
The seismic effect and the structural response (e.g. displacements, internal forces) are considered probabilistic variables that are approximated by a finite number of samples during the nonlinear analyses. Seismic excitation is described by 44 acceleration records from recent earthquakes that include some of the devastating ground motions in the past four decades (e.g. Kobe, Northridge, Chi-Chi etc.) Structural response is evaluated separately for the 44 records; this provides 44 samples for the structural response variable. The set of records is scaled to increasing levels of seismic intensity and the response of the structure is evaluated at each level. This provides a detailed understanding of the seismic performance of the structure that is summarized in fragility curves. Fragility curves describe the collapse probability of a structure at different seismic intensity levels. Design procedure evaluation is based on the fragility curves corresponding to each archetype.
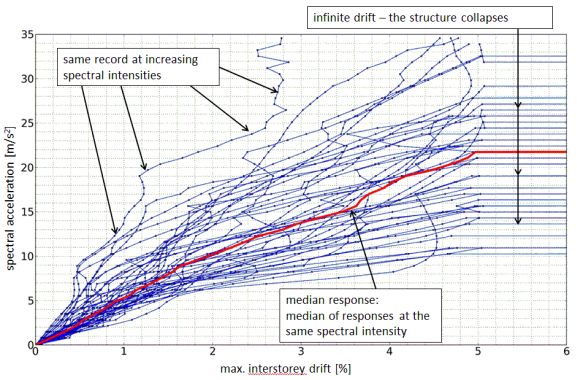
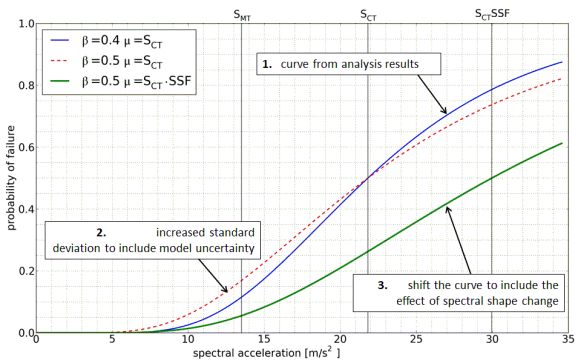
Figure 9 Result of nonlinear dynamic analyses and the corresponding fragility curves
Results
Laboratory experiments
Experimental tests with custom load protocols have verified the advantageous energy dissipation capabilities of BRB elements [Z3, Z4]. Sensitivity of BRB behaviour to the geometric proportions of the steel core has been highlighted through the results of two specimens. Disadvantageous core geometry leads to strong axis buckling near the transition zone of the core, and this eventually results in a failure mode that significantly reduces the energy dissipation capability of the element [Z5].

Figure 10. Significant deformation from strong axis buckling prior to failure near the transition zone of the steel core (left); no deformation experienced when proper core geometry is used(right)
Based on experimental results, I defined parameters required for practical BRB design and quality control in accordance with European standards. These parameters describe a bilinear stress-strain relationship and its acceptable variance [Z6].
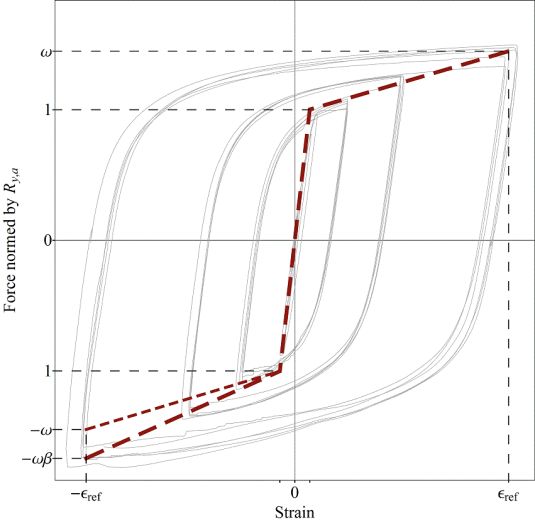
Figure 11. Simplified bilinear stress-strain relationship for practical design of BRB elements
Numerical model
I developed a custom BRB material model [Z7] in the OpenSEES open source finite element code [11]. When combined with a prismatic beam element, the new material model provides an effective and accurate representation of BRB behaviour that does not require large amounts of computational resources. The model is based on the Menegotto-Pinto steel material [12]. The kinematic hardening of the original material is extended with isotropic hardening. The original stress function is modified to include three asymptotes instead of two. With this modification, a stress limit can be introduced in the model that effectively describes the ultimate stress of the material. Load history dependence is also included in the new model, thus material behaviour is influenced by the previously taken path in the stress-strain plain. These characteristics are controlled independently under tension and compression, therefore the material model can handle the asymmetric BRB behaviour. I am not aware of any other steel material model with such small computational resource requirement and such large flexibility in application in the currently available finite element codes.
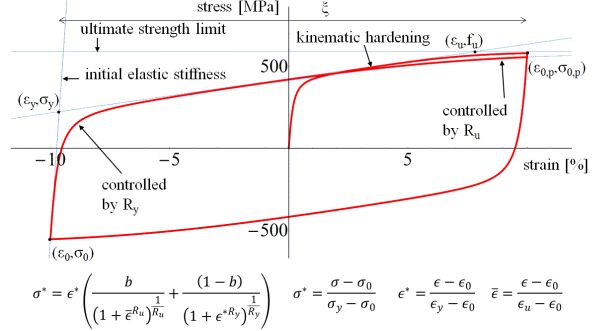
Figure 12 Characteristic stress-strain curves of the developed material model and the stress function that describes them
Design procedure evaluation framework
I developed a custom software for design procedure evaluation based on the OpenSEES environment. The software automatically produces the fragility curve of any archetype according to the complex methodology described in FEMA P695 [Z8, Z9]. I proposed modifications to the original methodology to reduce the uncertainty in the results. I noted that the original procedure is based on detailed investigation of reinforced concrete and wooden structures performed in California, thus its applicability to other structural systems (e.g. steel frames) and other regions shall be verified [Z10].
Our joint research with the University of Porto focuses on the extension of the original procedure so that it becomes applicable to any structural solution in any seismic region. We suggest using groups of record sets instead of the single set of 44 records. The record sets shall correspond to the seismic intensity and the vibrational properties of the structure under investigation [Z11]. Figure 13 shows the significant difference between the spectra that correspond to increasing levels of seismic intensity and structures with various natural periods. Record selection is facilitated by a web-based application that automatically provides the appropriate set for the given design scenario from a database of more than 10,000 earthquake records [13]. I developed a procedure that combines the results from several record sets and produces a single fragility curve, thus the extended methodology can be integrated in the original framework.

Figure 13. Comparison of so-called response spectra from earthquakes with increasing intensities at the same location (left); governing response spectra for structures with different vibrational properties (right).
Expected impact and further research
The design parameters defined from experimental results and the evaluated design procedure is expected to be included in a future revision of the Eurocode 8 standard through the work of the ECCS TC13 committee. Therefore, the investigated procedure is expected to define the design of BRB frames in Europe
The accuracy and efficiency of the developed numerical BRB model is expected to facilitate its integration in the official OpenSEES release. This would lead to its worldwide use in BRB related state-of-the-art research.
The extension of the original framework for design procedure evaluation is an important step towards a general solution for this problem. The proposed framework is expected to be capable of evaluating arbitrary anti-seismic solutions and lead to more economical design and a better understanding of structural behaviour under seismic excitation.
Besides the University of Porto, we are establishing joint research projects with several other European universities (Instituto Superior Técnico of Lisbon, University of Naples “Federico II”, Politechnica University of Timisoara, University of Oxford) to improve existing BRB designs and extend the application of BRBs to new areas.
Publications, references, links
Publications
[Z1] Budaházy V., Zsarnóczay Á., Vigh L.G., Dunai L., Numerical model development for cyclic hardening investigation of steel-yield based displacement dependent devices. Proc. 15th World Conference on Earthquake Engineering (15 WCEE), Lisbon, Portugal, pp. 1-10. paper 5222. (2012)
[Z2] Zsarnóczay Á., Vigh L.G., Kihajlásbiztos merevítőrúd ciklikus viselkedésének elemszintű modellezése - in Hungarian. XI. Magyar Mechanikai Konferencia, Miskolc, Hungary, 9 p. (2011)
[Z3] Zsarnóczay Á., Vigh L.G., Experimental analysis of buckling restrained brace behaviour under cyclic loading. 28th Danubia – Adria – Symposium on Advances in Experimental Mechanics, Siófok, Hungary, pp. 297-298. (2011)
[Z4] Zsarnóczay Á., Vigh L.G., Kihajlásbiztos merevítőrudak kísérleti vizsgálata - in Hungarian. Magyar Építőipar LXII:(6) pp. 222-230. (2012)
[Z5] Zsarnóczay Á., Vigh L.G., Experimental analysis of buckling restrained braces: Performance evaluation under cyclic loading. Proceedings of EUROSTEEL 2011 – 6th European Conference on Steel and Composite Structures. Budapest, Hungary, pp. 945-950. (2011)
[Z6] Zsarnóczay Á., Budaházy V., Vigh L.G., Dunai L., Cyclic hardening criteria in EN 15129 for steel dissipative braces. Journal of Constructional Steel Research 83, pp. 1-9. (2013)
[Z7] Zsarnóczay Á., Budaházy V., Uniaxial Material Model Development for Nonlinear Response History Analysis of Steel Frames. Proc Second Conference of Junior Researchers in Civil Engineering, Budapest, Hungary, pp. 307-317 (2013)
[Z8] Zsarnóczay Á, Seismic Performance evaluation of buckling restrained braces and frame structures. Proc 9th fib International PhD Symposium in Civil Engineering, Karlsruhe, Germany, pp. 195-200 (2012)
[Z9] Zsarnóczay Á., Influence of Plastic Mechanism Development on the Seismic Performance of Buckling Restrained Braced Frames – case study. Proc. Conference of Junior Researchers in Civil Engineering, Budapest, Hungary, pp. 289-297 (2012)
[Z10] Zsarnóczay Á., Vigh L.G., Capacity design procedure evaluation for buckling restrained braced frames with incremental dynamic analysis. Proc. 15th World Conference on Earthquake Engineering (15 WCEE), Lisbon, Portugal, pp. 1-10. paper 3533. (2012)
[Z11] Zsarnóczay Á., Macedo L., Castro J.M., Vigh L.G., A novel ground motion record selection strategy for Incremental Dynamic Analysis. Proc. Vienna Congress on Recent Advances in Earthquake Engineering and Structural Dynamics, (2013) (submitted)
Links:
References:
[1] EN 1998-1:2008, Eurocode 8: design of structures for earthquake resistance – part 1: general rules, seismic actions and rules for buildings. CEN (2008)
[2] Watanabe A., Hitomi Y., Saeki E., Wada A., Fujimoto M., Properties of Brace Encased in Buckling-Restraining Concrete and Steel Tube. Proc. Ninth World Conference on Earthquake Engineering IV. pp. 719-724 (1988)
[3] López WA, Sabelli R, Seismic design of buckling restrained braced frames. Steel Tips (2004)
[4] ANSI/AISC 341-10. Seismic provisions for structural steel buildings. AISC (2010)
[5] Romero P., Reaveley L.D., Miller P.J., Okahashi T.O., Full scale testing of WC series buckling-restrained braces – test report. Salt Lake City: Department of Civil & Environmental Engineering, The University of Utah (2007)
[6] Merritt S., Uang Ch.M., Benzoni G., Subassemblage testing of star seismic buckling restrained braces – test report. San Diego: Department of Structural Engineering, University of California (2003)
[7] EN 15129, Anti-seismic devices. CEN (2010)
[8] Budaházy V., Modelling of the hysteretic behaviour of buckling restrained braces. Proc Conference of Junior Researchers in Civil Engineering, Budapest, Hungary, pp. 34-41 (2012)
[9] FEMA P695, Quantification of building seismic performance factors. Federal Emergency Management Agency, Washington, D.C. (2009)
[10] Vamvatsikos, D. and Cornell, C.A., Incremental dynamic analysis. Earthquake Engineering and Structural Dynamics. 31: 491-514. (2002)
[11] McKenna F., Feneves G.L., Open system for earthquake engineering simulation. Pacific Earthquake Engineering Research Center, (2012)
[12] Menegotto, M., Pinto, P., Method of Analysis for Cyclically Loaded Reinforced Concrete Plane Frames Including Changes in Geometry and Nonelastic Behavior of Elements under Combined Normal Force and Bending. IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well-Defined Repeated Loads, Final Report, Lisbon (1973)
[13] PEER NGA Database: http://peer.berkeley.edu/peer_ground_motion_database
