|
|
BMe Research Grant |
|
Doctoral School of Physics
Department of Physics / Institute of Physics
Supervisor: Dr. BOKOR Nándor
Optimization of the focal spot in high numerical aperture systems
Introducing the research area
My research is centered around the optimization of the focal spot of strongly focused laser beams and determining the illumination that corresponds to the optimal focal spot. I created theoretical models and numerical algorithms that can be applied more easily and to a more general class of problems than existing methods. I proposed a numerically stable procedure for calculating novel sets of vector functions which can also be useful in research areas other than optics, such as geophysics.
Brief introduction of the research place
My PhD work has been carried out as a member of the Optical Metrology Group at the Department of Physics. Research interests of the group include coherent and incoherent optical metrology, holography and image processing, as well as the investigation of high numerical aperture systems. We perform our research in the latter field in collaboration with the Olympus Corporation (Japan) and the Weizmann Institute of Science (Israel).
History and context of the research
|
|
|
Figure 1: Confocal microscope in use: a practical application of strongly focused laser beams [F1] |
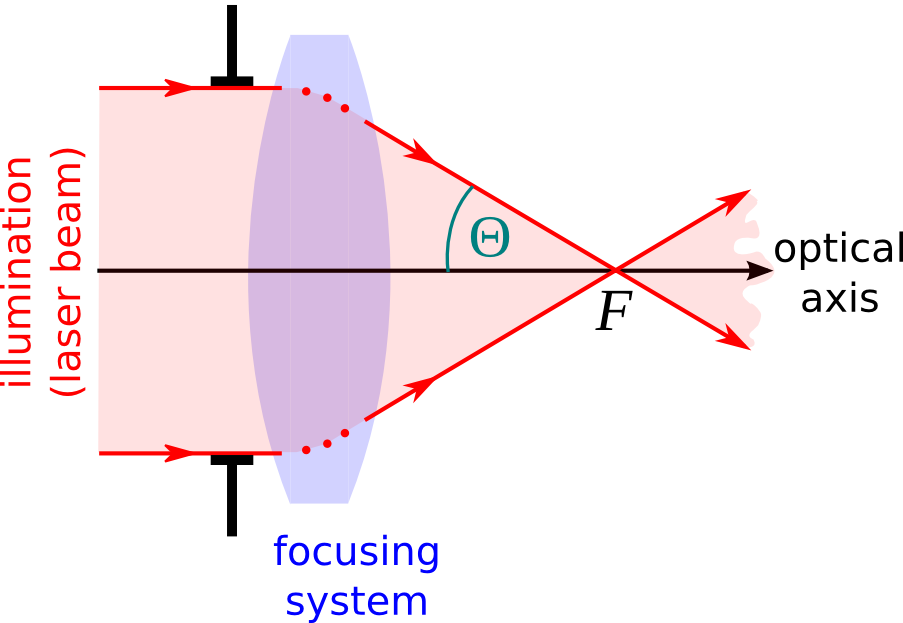
Applied optics includes several fast evolving research areas – for instance, laser scanning microscopy [1] (see Fig. 1), optical trapping of nanoparticles [2] or nanolithography [3] – where focusing the light into the smallest spot possible, and controlling certain properties of the focal spot, such as spatial intensity and/or polarization distribution is crucial. Therefore, the illuminating laser beam has to be focused using a so-called high numerical aperture optical system (NA > 0.6) where the value of NA (in air) is equal to the sine of the apex angle Θ of the cone of light reaching the focus (see Fig. 2). In practice, microscope objectives are often used as high NA focusing systems.
|
|
|
Figure 2: sketch of focusing of a laser beam |
For high NA systems, classical approximation methods of physical optics (such as the paraxial approximation and scalar diffraction theory) cannot be employed, hence electric and magnetic fields require a full-vectorial treatment. While the Debye–Wolf vectorial diffraction theory [4, 5] is mostly used in such a situation, the multiple theory of focusing [6] is worth mentioning as well, as an alternative theoretical description of high NA focusing. This latter theory considers the focal field, i.e. the electric field in the vicinity of the focus, as a linear combination of vector multipole fields, which are well known from multipole radiation theory.
In addition to calculating the focal field of given illuminations, the inverse problem is highly important, too. Our goal here is to find the illumination (the electric field at the entrance pupil of the focusing system) which corresponds to a focal spot exhibiting a given distribution of intensity and polarization. Although [7-12] literature provides solutions for special cases, we do not know a single method that is generally applicable and takes the whole focal volume into account.
The research goal, open questions
First I considered the problem of constructing a phase-only mask that results – when the modulated laser beam is focused by a high NA lens – in a prescribed intensity profile in the focal plane. One possible solution to this problem is the vectorial adaptation of the paraxial Gerchberg–Saxton iterative Fourier transform algorithm [13]. There exists a case developed for linearly polarized illumination [7], however, I set out to generalize the Gerchberg–Saxton method to be applicable to illuminations with an arbitrary polarization state.
In the second part of my PhD research, I constructed vectorial basis functions that carry a physical meaning and are well-suited to the solution of inverse problems. They are required to represent physically realizable focal fields (i.e. be solutions to the vectorial Helmholtz equation [14]) and to exhibit the directionality which characterizes focused beams as a consequence of the illumination coming from a restricted solid angle specified by the angular semiaperture Θ. In addition, I demanded that the new vector functions be quickly and easily calculable and enable us to extend the optimization of the focal spot to the three-dimensional focal volume, too.
Methods and results
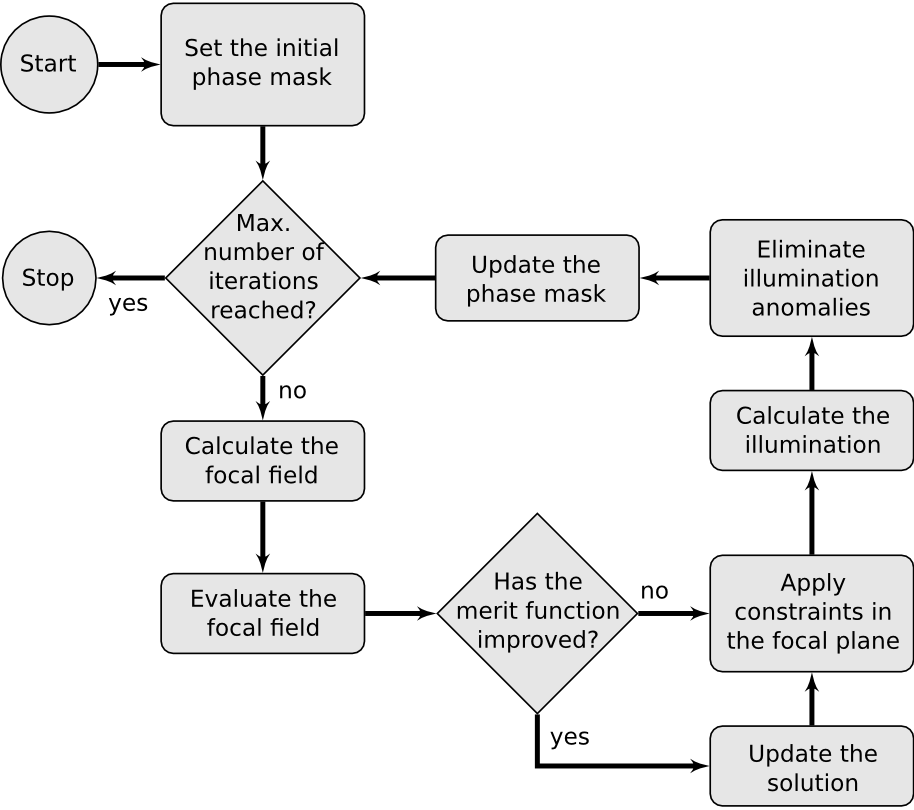
The vectorial generalization of the iterative Fourier transform algorithm is based on the Debye–Wolf theory [4, 5]. The flow chart of the procedure is depicted in Fig. 3. By repeating the proposed iterative process, the methods converges to a solution that (approximately) satisfies the imposed focal constraints and gives us a corresponding phase mask.
|
|
|
Figure 3: Flow chart of the process for the iterative design of phase masks |
I demonstrated the method for so-called flat-top intensity profiles (i.e. homogeneous intensity within a given region and vanishing intensity outside), which were prescribed in the focal plane. As a merit function, I considered the squared difference between the prescribed and calculated intensities, integrated over the flat-top region. It is worth mentioning that homogenizing the intensity inside the flat-top region results in non-physical effects in the retrieved illumination, such as the appearance of a non-transverse polarization component or non-zero electric field outside the entrance pupil. These anomalies have to be corrected before extracting the phase information at the end of each cycle. As the solution to the optimization problem, I considered the phase mask resulting in the minimal value of the merit function. In comparison with the method suggested by Jabbour and Kuebler [7], the proposed technique resulted in phase masks which led to an increase in diffraction efficiency by 11-22% [J1].
The second research topic, a novel representation of the focal field which aids the solution of inverse problems, emerged from the marriage of two unrelated theories: I solved the so-called concentration problem [15] (which is well-known in signal processing and geophysics) for the case of vector multipole fields, a cornerstone of the multipole theory of focusing [16].
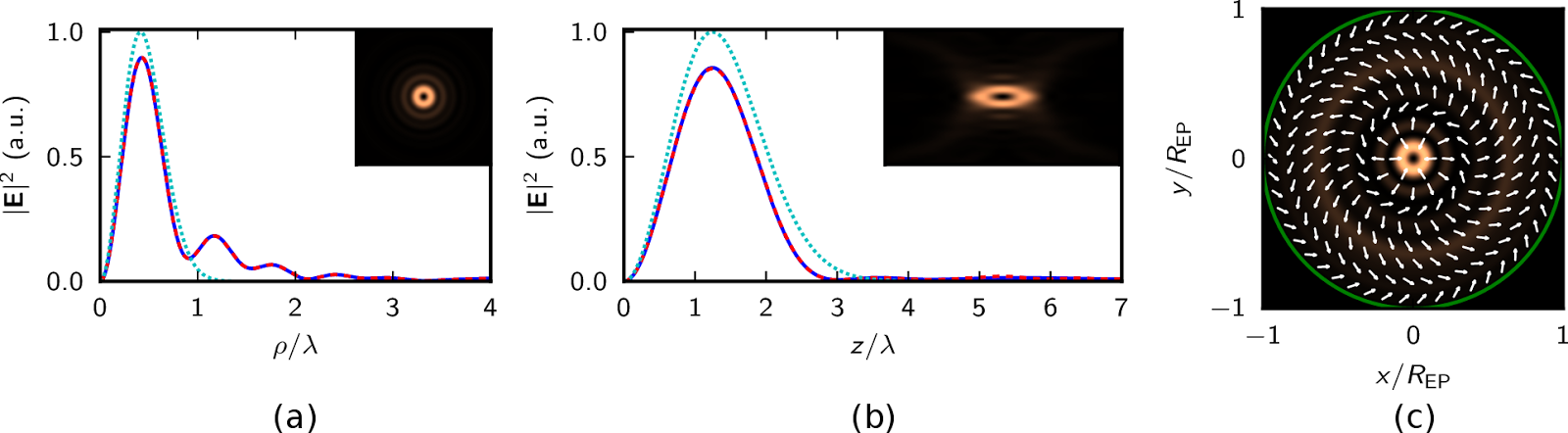
The concentration problem – pioneered by D. Slepian and his colleagues [17-20] – is a problem of finding a band-limited function whose energy is concentrated to a finite spatial or temporal region as much as possible. I formulated the concentration problem for the case of vector spherical harmonics [16], which represent the plane-wave (angular) spectrum of vector multipole fields. As a result, I obtained vector functions which are (almost completely) confined to a spherical cap with a half apex angle of Θ. I called these functions vector Slepian harmonics. They determine novel focal fields with a directional character called vector Slepian multipole fields [J2]. Figure 4 shows the intensity distribution of a concentrated vector Slepian harmonic and that of the corresponding vector Slepian multipole field.
|
|
Figure 4: (a) the angular intensity distribution of a vector Slepian harmonic whose energy is almost completely concentrated to the spherical cap marked with a circle in magenta and specified by the NA of the system (NA = 0.85). The half apex angle Θ of the spherical cap is approximately 58 degrees. The arrows in cyan depict the polarization state. To the right, one can see the intensity distribution of the corresponding vector Slepian multipole field (focal field) in (b) the focal plane and (c) in an arbitrary meridional plane.
|
With help of the novel Slepian-type basis functions, the inverse problem of high NA focusing can be separated into two main steps: first we construct a focal field as a superposition of a finite number of vector Slepian multipole fields in such a way that it fulfils a constraint prescribed in the focal volume in an optimal way (e.g. it approximates a prescribed intensity profile in a least-squares sense). Usually this task is translated into a non-linear optimization problem that results in the coefficients of the optimal focal field. In the second step we combine the corresponding vector Slepian harmonics using the newly obtained coefficients to construct the plane-wave spectrum of the focal field. Given this plane wave spectrum, the illumination at the entrance pupil can be constructed in a straightforward way [J3].
The applicability of the process above was demonstrated for three well-known focal intensity distributions, the so-called optical needle [11], optical tube [12] and optical bubble [21]. Results for the optical bubble are shown in Fig. 5.
It is a common property of all concentration problems that they require the solution of the eigenvalue problem of an ill-conditioned integral operator, the so-called concentration operator [22]. We encounter the same situation in the case of vector Slepian harmonics and this can cause severe numerical instabilities. However, in certain scalar concentration problems there exists a Sturm–Liouville [23] differential operator that commutes with the concentration operator and whose eigenvalue problem can be solved without any difficulties, hence numerical problems can be avoided [15]. Until recently, I have not been aware of such a differential operator for the concentration problem of vector spherical harmonics (which also emerges when calculating the vector Slepian harmonics).
Luckily, I succeeded in transforming the above vector concentration problem into another scalar problem and in finding a commuting differential operator for that case [J4]. Based on this novel operator, I proposed a fast and numerically stable algorithm for calculating the vector Slepian harmonics.
Expected impact and further research
My research papers [J1-J4] have received 14 independent citations to date. The vectorial adaptation of the iterative Fourier transform algorithm is cited in a chapter of Progress in Optics [25]. I presented my results at two international conferences [J5, J6].
Vector Slepian harmonics turned out to be not only useful in optics but in geophysics as well [24]. Since their numerically stable calculation is a central issue, my results regarding the commuting differential operator are cited in the forthcoming second edition of Handbook of Geomathematics [26].
There are various ways of enhancing and extending the proposed methods. It would be worth investigating the extension of the vectorial iterative Fourier transform method to the case of three-dimensional constraints in the focal volume. For the scalar case, there exist such generalizations in literature [27, 28].
Regarding the Slepian-type vector functions, several possible directions of research emerge as well: on the one hand, it would be feasible to find more effective optimization methods to approximate the prescribed intensity profile using vector Slepian multipole fields, on the other hand, their numerical evaluation could be fine-tuned to yield a faster optimization process. A comparison with other methods found in the literature [10, 11] would be interesting and instructive as well.
Publications, references, links
Publications
[J1] K. Jahn and N. Bokor. Intensity control of the focal spot by vectorial beam shaping. Opt. Commun., 283(24):4859–4865, 2010.
[J2] K. Jahn and N. Bokor. Vector Slepian basis functions with optimal energy concentration in high numerical aperture focusing. Opt. Commun., 285(8):2028–2038, 2012.
[J3] K. Jahn and N. Bokor. Solving the inverse problem of high numerical aperture focusing using vector Slepian harmonics and vector Slepian multipole fields. Opt. Commun., 288:13–16, 2013.
[J4] K. Jahn and N. Bokor. Revisiting the Concentration Problem of Vector Fields within a Spherical Cap: A Commuting Differential Operator Solution. J. Fourier Anal. Appl., 20(2):421–451, 2014.
[J5] K. Jahn and N. Bokor: Using a vector Slepian basis in high numerical aperture focusing. Conference poster. Focus on Microscopy 2011, Konstanz.
[J6] K. Jahn and N. Bokor. Vector Slepian functions and the inverse problem of high numerical aperture focusing. Proc. SPIE, 8550:855038, 2012.
Links
Information about microscopy techniques:
Olympus Microscopy Resource Center
Homepages of researchers and research groups:
Research group of Colin Sheppard
Research group of Nir Davidson
Research group of Frederik Simons
The Institute of Optics, University of Rochester
Two-Photon Imaging Center (Budapest)
References
[1] P. Török and F.-J. Kao. Optical Imaging and Microscopy: Techniques and Advanced Systems. Springer, Berlin, second edition, 2007.
[2] A. Ashkin. Optical trapping and manipulation of neutral particles using lasers. Proc. Natl. Acad. Sci. USA, 94:4853–4860, 1997.
[3] T. Itani, W. Wakamiya, J. Cashmore, and M. Gower. 157-nm lithography with high numerical aperture lens for sub-70 nm node. Microelectron. Eng., 67:39–46, 2003.
[4] E. Wolf. Electromagnetic diffraction in optical systems. I. An integral representation of the image field. Proc. R. Soc. London Ser. A, 253 (1274):349–357, 1959.
[5] B. Richards and E. Wolf. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. Proc. R. Soc. London Ser. A, 253(1274):358–379, 1959.
[6] C. J. R. Sheppard and P. Török. Efficient calculation of electromagnetic diffraction in optical systems using a multipole expansion. J. Mod. Opt., 44(4):803–818, 1997.
[7] T. G. Jabbour and S. M. Kuebler. Vectorial beam shaping. Opt. Express, 16(10):7203–7213, 2008.
[8] R. Kant. Superresolution and increased depth of focus: an inverse problem of vector diffraction. J. Mod. Opt., 47(5):905–916, 2000.
[9] M. R. Foreman, S. S. Sherif, P. R. T. Munro, and P. Török. Inversion of the Debye–Wolf diffraction integral using an eigenfunction representation of the electric fields in the focal region. Opt. Express, 16(7):4901–4917, 2008.
[10] J. J. M. Braat, P. Dirksen, A. J. E. M. Janssen, S. van Haver, and A. S. van de Nes. Extended Nijboer–Zernike approach to aberration and birefringence retrieval in a high-numerical-aperture optical system. J. Opt. Soc. Am. A, 22(12):2635–2650, 2005.
[11] J. Wang, W. Chen, and Q. Zhan. Engineering of high purity ultra-long optical needle field through reversing the electric dipole array radiation. Opt. Express, 18(21):21965–21972, 2010.
[12] J. Wang, W. Chen, and Q. Zhan. Three-dimensional focus engineering using dipole array radiation pattern. Opt. Commun., 284(12):2668–2671, 2011.
[13] R. W. Gerchberg and W. O. Saxton. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik (Jena) 35:237, 1972.
[14] J. D. Jackson. Classical Electrodynamics. Wiley, Hoboken, NJ, third edition, 1999.
[15] F. J. Simons, . A. Dahlen, F, and M. A. Wieczorek. Spatiospectral concentration on a sphere. SIAM Rev., 48(3):504–536, 2006.
[16] N. J. Moore and M. A. Alonso. Closed-form bases for the description of monochromatic, strongly focused, electromagnetic fields. J. Opt. Soc. Am. A, 26(10):2211–2218, 2009.
[17] D. Slepian and H. O. Pollak. Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty–I. Bell Syst. Tech. J., 40(1):43–63, 1961.
[18] H. J. Landau and H. O. Pollak. Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty–II. Bell Syst. Tech. J., 40(1):65–84, 1961.
[19] H. J. Landau and H. O. Pollak. Prolate Spheroidal Wave Functions,Fourier Analysis and Uncertainty–III: The Dimension of the Space of Essentially Time- and Band-limited Signals. Bell Syst. Tech. J., 41(4):1295–1336, 1962.
[20] D. Slepian. Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty–IV: Extensions to Many Dimensions; Generalized Prolate Spheroidal Functions. Bell Syst. Tech. J., 43(6):3009–3057, 1964.
[21] N. Bokor and N. Davidson. A three dimensional dark focal spot uniformly surrounded by light. Opt. Commun., 279(2):229–234, 2007.
[22] B. Bell, D. B. Percival, and A. T. Walden. Calculating Thomson’s spectral multitapers by inverse iteration. J. Comput. Graph. Stat., 2(1):119–130, 1993.
[23] G. B. Arfken, H. J. Weber, and F. E. Harris. Mathematical Methods for Physicists: A Comprehensive Guide. Academic Press/Elsevier, Waltham, MA, 7th edition, 2012.
[24] A. Plattner and F. J. Simons. Spatiospectral concentration of vector fields on a sphere. Appl. Comput. Harmon. Anal., 36(1):1–22, 2014.
[25] Z. Chen, H. Limin and P. Jixiong. Tight Focusing of Light Beams: Effect of Polarization, Phase, and Coherence. In Progress in Optics 57:219-259, 2012.
[26] A. Plattner and F. J. Simons. Potential-field estimation using scalar and vector Slepian functions at satellite altitude. In W. Freeden, M. Z. Nashed, and T. Sonar, editors, Handbook of Geomathematics. Springer, Berlin, second edition. to appear.
[27] G. Shabtay. Three-dimensional beam forming and Ewald’s surfaces. Opt. Commun., 226(1):33–37, 2003.
[28] G. Whyte and J. Courtial. Experimental demonstration of holographic three-dimensional light shaping using a Gerchberg–Saxton algorithm. New J. Phys., 7(1):117, 2005.
[F1] Source: http://www.sciencephoto.com/media/112553/enlarge