Matematika- és Számítástudományok Doktori Iskola 

BME TTK, Sztochasztika Tanszék/Matematika Intézet

Témavezető: Dr. Simon Károly

Legrövidebb utak aszimptotikus viselkedése véletlen gráfokban

A kutatási téma néhány soros bemutatása

Az elmúlt pár évtizedben számos tudományterületen vált szükségessé a nagy méretű komplex hálózatok, mint pl. az Internet jobb megismerése. Matematikai modellként szolgálnak a különböző véletlen gráf modellek, melyek egy-egy valós hálózat tulajdonságait igyekeznek megragadni. Kutatásaim egyik fő iránya annak vizsgálata, hogy milyen modellek rendelkeznek az ún. „kis világ” tulajdonsággal, és annak milyen következményei vannak.

A kutatóhely rövid bemutatása

Doktori tanulmányaimat a Sztochasztika Tanszéken végzem Dr. Simon Károly témavezetésével. A tanszék több munkatársa nemzetközileg elismert szakember. A kutatócsoportban aktív tudományos élet folyik: a tanszékhez szorosan kapcsolódik az MTA Sztochasztika Kutatócsoportja; a Sztochasztika és Dinamikai Rendszerek szemináriumokon rendszeresen adnak elő meghívott külföldi vendégek és a tanszéken fut több OTKA és TÁMOP projekt, valamint együttműködés ipari partnerekkel.

A kutatás történetének, tágabb kontextusának bemutatása

„Kicsi a világ”– szoktuk mondani, amikor például két ember váratlanul talál egy távolinak tűnő közös ismerőst. Valóban, gyakori jelenség valós hálózatok esetén, hogy csupán néhány kapcsolat mentén el lehet jutni bárhonnan bárhova. Komplex hálózatok modellezésére szolgál a véletlen gráfok elmélete, mely mára az alkalmazott valószínűségszámítás rendkívül dinamikusan fejlődő ágává nőtte ki magát.

A véletlen gráfok elméletét Erdős Pál és Rényi Alfréd úttörő munkája [10] indította útjára az 1960-as évek elején. Modelljükben egy  csúcsú gráf minden lehetséges csúcspárjára egymástól függetlenül feldobunk egy ugyanolyan (hamis) érmét, és fej esetén húzunk egy élt a két csúcs közt, írás esetén pedig nem. Megmutatták, hogy a modell rendelkezik a „kis világ” tulajdonsággal, amely matematikailag annyit tesz, hogy a gráfban a legrövidebb utak logaritmikusan skálázódnak a gráf csúcsainak számával.

A modell azonban nem rendelkezik más, a valós hálózatokra jellemző egyéb fontos tulajdonságokkal, úgy mint hatványrendű fokszámeloszlás, magas klaszterezettség, inhomogenitás vagy hierarchikus  szerkezet [2,5,6,7,13,14]. Ebből adódóan számos modell született az utóbbi időben.

Legrövidebb utak keresése konkrét gráfokban klasszikus gráfelméleti probléma, mely algoritmikusan hatékonyan megoldható. Véletlen gráfok esetén csupán a modell dinamikájából, annak időbeli fejlődéséből lehetséges pontosan meghatározni a legrövidebb utak várható hosszát, mely konkrét realizációtól függetlenül érvényes lesz. Jelenleg ez a kihívásokkal teli, sokakat érdeklő téma [1,3,4,5,7,9,11,12] egyik kutatási területem.

 

A kutatás célja, a megválaszolandó kérdések

A véletlen gráfok egyik célja olyan modellek bevezetése, amelyek jól tükrözik valamely valós hálózat tulajdonságait, ugyanakkor még analitikusan kezelhetők maradnak. Kutatásaimban eddig két modellel foglalkoztam behatóan:

 

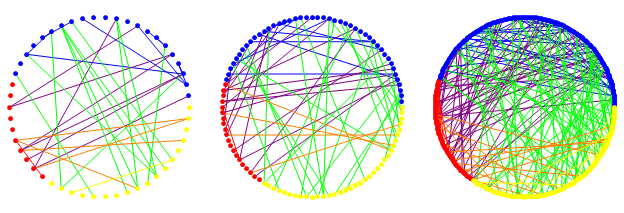
1. Inhomogén véletlen gráf (IHRG)[5]: az Erdős-Rényi gráfok egy természetes általánosításaként értelmezhető. A csúcsoknak egy véges halmazból sorsolunk egy-egy típust (előre rögzített arányokban), és aszerint, hogy két csúcs milyen típusú, különböző hamis érméket dobunk fel. A modell erőssége, hogy a paraméterek rugalmas megválaszthatóságának köszönhetően több, egyéb modell is ennek speciális esete. Az alábbi ábrán egy 50,100 illetve 300 csúcsú IHRG látható három típussal.

 

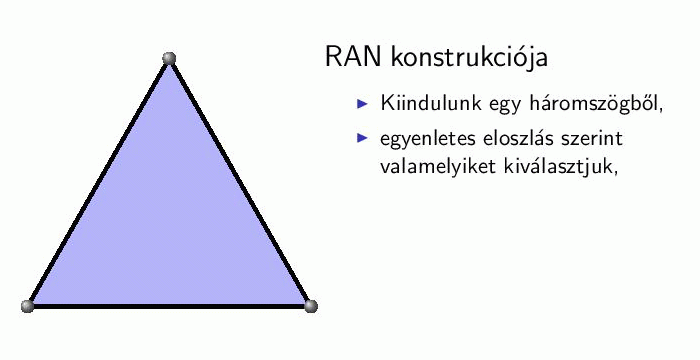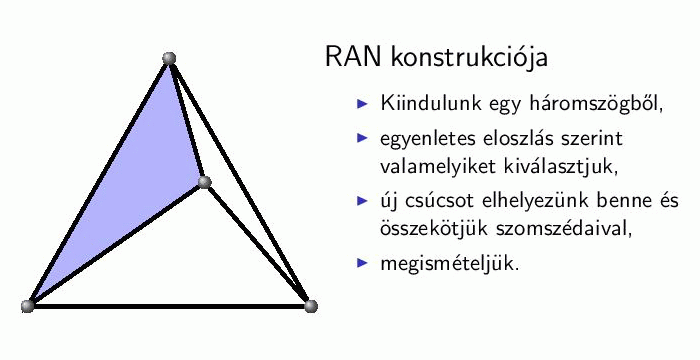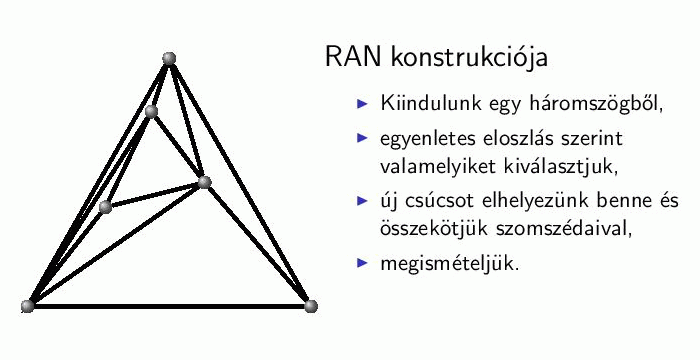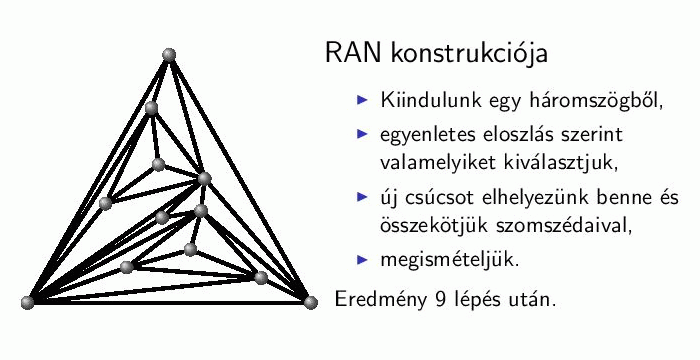
2. Véletlen Apolloniai hálózat (RAN)[13,14]: az Apolloniai körpakolás problémájából eredeztethető gráf, melyet két dimenzióban könnyű elképzelni. Egy háromszögből kiindulva minden lépésben kiválasztunk egyenletes eloszlás szerint egy háromszöget, aminek a belsejébe elhelyezünk egy csúcsot és összekötjük a kiválasztott háromszög csúcsaival. Ezt az eljárást ismételjük. A modell gond nélkül általánosítható tetszőleges d-dimenzióba d-dimenziós szimplexekkel.

 

 

Élsúlyozott gráfokban legrövidebb utak meghatározásakor elsődleges cél meghatározni az út hosszát és a rajta lévő élek számát (amelyek élsúlyozatlan esetben megegyeznek). Három alapvető kérdést szokás vizsgálni:

1. két véletlenszerűen választott csúcs közt mekkora az út?

2. egy rögzített csúcsból a többibe vezető legrövidebb út közül a maximális mekkora?  

3. a gráf átmérője (azaz az összes legrövidebb út közül a maximális) mekkora?

Az IHRG esetén exponenciális élsúlyokkal vizsgáltuk e kérdéseket, míg a RAN-ok esetén az élsúlyozatlan esetben. Elsődleges cél volt igazolni a kis világ tulajdonságot.

Módszerek

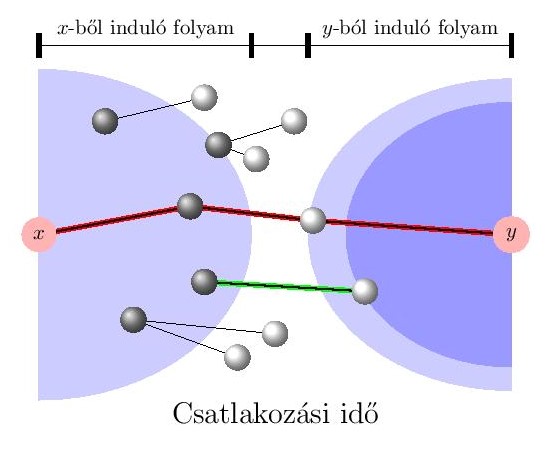
A bizonyítások menetének heurisztikája mindkét esetben könnyen követhető, de a precíz formalizmushoz számos módszer sikeres alkalmazása szükséges. A gráf egy csúcsából indított keresési bejárást legszemléletesebb egy a gráf élein terjedő egységnyi sebességű folyamként elképzelni. Amikor a folyam elér egy másik csúcsot, akkor megtaláltuk a legrövidebb utat a két csúcs között, és az eltelt idő adja az út hosszát. Több szempontból célszerű mindkét csúcsból egyszerre elindítani egy-egy folyamot és várni míg nem csatlakoznak.

Nagy gráfokban gyakori, hogy egy csúcs környezetének felderítése az elején fa struktúrát mutat, azaz nem találunk köröket. Ha ismert, hogy egy csúcs szomszédai milyen eloszlást követnek, akkor lokálisan ez a keresési bejárás egy folytonos idejű elágazó folyamathoz csatolható. Ez lényeges, mert így az elágazó folyamatok kiterjedt irodalmából lehet közvetlenül alkalmazni eredményeket. Az IHRG-nél ez a helyzet, míg a RAN-nál másképp kerülnek elő az elágazó folyamatok.

A legnagyobb kihívást a két folyam csatlakozásának precíz leírása adja. Ugyanis nem tudjuk a két folyamot folytonos időben követni, csak diszkrét lépésekben ahogy újabb és újabb csúcsok kerülnek felfedezésre egyik, illetve másik folyamban. Akkor találjuk meg potenciálisan a legrövidebb utat, ha felfedezésre kerül egy-egy olyan csúcs az egyik, illetve a másik folyamban, melyek közt fut él (ábrán zöld él). Azért csak potenciális jelölt, mert előfordulhat, hogy kicsivel később találunk másik két hasonló csúcsot, melyek közt futó él súlyával együtt már kisebb lesz az összsúly (ábrán piros út). Tehát a potenciális jelöltek közül a minimális súlyú adja a legrövidebb utat.

További technikai nehézséget okoz a különböző típusok kezelése, illetve tételeink absztrakt típus-terekre is érvényesek, melyek bizonyítása véges típusúak ügyes approximációjával történik.

Egy RAN viszont egyáltalán nem lokálisan körmentes. Helyette a gráf hierarchikus szerkezetét lehet kihasználni. A gráf egy csúcsához kölcsönösen egyértelműen meg lehet feleltetni egy kódot, melyből pontosan kiolvasható, hogy kik az ő szomszédai, mikor megszületik. Ennek köszönhetően az élek megfelelő csoportosítása felfedi a gráf fa-szerű szerkezetét.

A gráf diszkrét fejlődése beágyazható egy folytonos idejű folyamatba, melynek köszönhetően az élek egyik csoportja ismét egy folytonos idejű elágazó folyamattal azonosítható. Az elágazó folyamat tipikus és maximális mélységét kell meghatározni. A többi él mentén rövidíteni lehet az úton, melyek eloszlása a  valószínűségszámításban ismert kupongyűjtögető problémájához vezet. A bizonyításhoz szükséges alkalmazni a felújítás elméletet, nagy eltérés tételeket, momentum módszereket és megoldani egy nem triviális feltételes szélsőérték feladatot.

Az analitikus módszereket kiegészítve szimulációkat is végeztem, melyek segítettek sejtések megfogalmazásában, és alátámasztották eredményeinket.

Eddigi eredmények

Mindkét modellről sikerült belátni, hogy teljesítik a kis világ tulajdonságot, azaz a vizsgált mennyiségek a gráf csúcsainak számának (-nel jelölve) növekedésével logaritmikusan skálázódnak.

Az IHRG esetén két véletlenszerűen választott csúcs közt a legrövidebb úton lévő élek száma megfelelő standardizálás után egy centrális határeloszlást követ ahogy  tart végtelenhez. Tehát pontosan meghatározható az élek várható számának nagyságrendje, ami  alakú, illetve a várható érték körüli koncentráció, és a szórás mértéke is, amely . A  és  konstansok a gráf egy konkrét realizációjától függetlenül, csupán a paraméterekből determinisztikusan meghatározhatók. Hasonlóan a legrövidebb út súlya  alakú, ahol a  egy determinisztikus míg  egy véletlen konstans. Ezzel sikerült általánosítani [4] eredményeit, ahol az Erdős-Rényi modellre bizonyítottak hasonlót.

A RAN modell esetén is sikerült centrális határeloszlás tételt (CHT) bizonyítani. A várható érték  nagyságrendű, a szórás pedig , ahol a  és  konstansok most is determinisztikusan meghatározhatók, realizációtól függetlenek. Természetesen a legrövidebb úton lévő élek száma egyenlő az út súlyával, hisz a gráf élsúlyozatlan. Legjobb tudomásunk szerint ez az első élsúlyozatlan eset, ahol sikerült CHT-t bizonyítani.

Továbbá, az egy rögzített csúcsból a többibe vezető legrövidebb út közül a maximális hosszára és a gráf átmérőjére is igazoltuk, hogy aszimptotikusan logaritmikusan skálázódnak a megfelelő konstansokkal. Ez sokkal nehezebb feladat, sok modellben nem is ismert. Érdekesség, hogy velünk párhuzamosan mások [8,9] is foglalkoztak a modellel, teljesen eltérő módszerekkel, de a mienkkel sikerült a legtöbbet bizonyítani.

A folyamok csatlakozását leíró lemmának van egy fontos következménye [K14]. Lényegi mondanivalója, hogy ha egyszerre indítjuk a két folyamot, akkor a csatlakozásig nagyságrendileg csupán  csúcsot kell felfedezni. Ezzel szemben ha csak az egyikből indítunk kereső bejárást, akkor már -nel arányos. Ebből következik, hogy a legrövidebb út megkeresése  időről az IHRG esetén -re csökken, míg a RAN esetén még nagyobb a különbség: ott  lesz. Sejtés, hogy kis világokra a jelenség általában igaz.

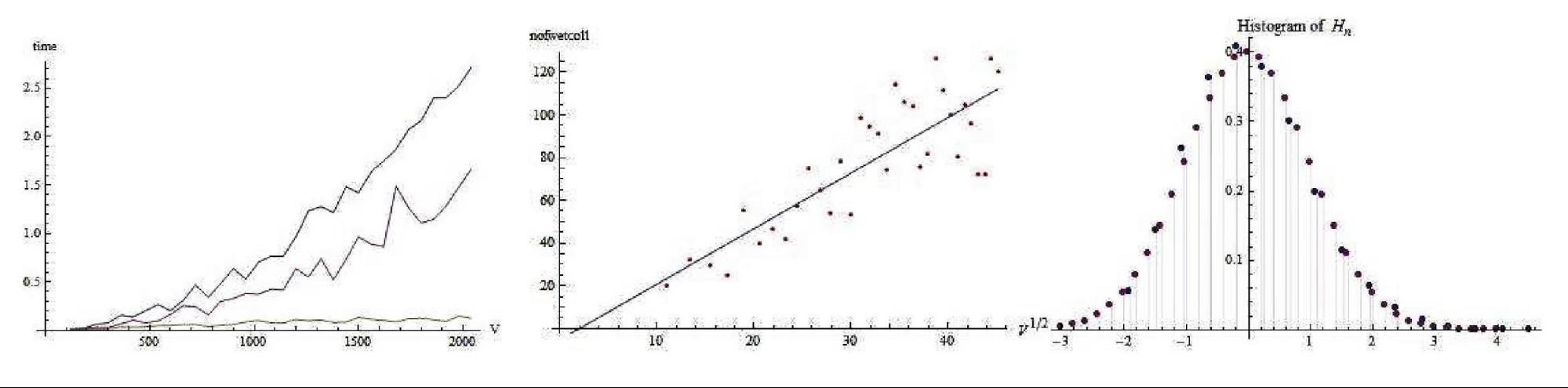
Analitikus eredményeinket szimulációk is szépen alátámasztják. A bal oldali ábrán látható a futási időben a jelentős különbség az egyszerre indított két folyam javára. A középsőn pedig az, hogy -ben valóban lényegében lineáris, hogy hány csúcsot fedez fel a két folyam. A jobboldalin pedig már 270 csúcsú gráf esetén is szépen kirajzolódik a CHT által jósolt harang görbe a legrövidebb úton lévő élek számának hisztogramján.

Várható impakt, további kutatás

Az eredmények közlésére több fórumon is sor került, úgy mint nemzetközi konferencián, workshopon illetve szemináriumon tartott előadás vagy poszter keretében. Az IHRG-ről szóló cikk [KK15] most jelent meg az Advances in Applied Probability folyóiratban. Ugyanebben a folyóiratban került elfogadásra a RAN-ról szóló cikk [KKV15] is. Mindkét munkára történt már független hivatkozás.  

Szeptembertől elnyertem egy fiatal kutatói állást a MTA Rényi Alfréd Matematikai Kutatóintézetében, ahol a Limits of Structures Lendület kutatócsoport tagjaként kiváló lehetőségem lesz folytatni a hasonló irányba mutató kutatásokat. Emellett szeretnék aktív maradni egyéb érdeklődési területemen is, mint a gráfok limeszei [KR11], a fraktálok [BK15] és a felújitási folyamatok [KT11].

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

[KK15] I. Kolossváry, J. Komjáthy (2015). First Passage Percolation on Inhomogeneous Random Graphs. Advances in Applied Probability 47, 589-610.  

[KKV15]  I. Kolossváry, J. Komjáthy, L. Vágó (2015). Degrees and distances in random and evolving Apollonian networks. elfogadva Advances in Applied Probability.  

[K14] I. Kolossváry (2014). Some consequences of the connection of exploration processes in small worlds. Technical report, preprint.

[BK15] B. Bárány, I. Kolossváry (2015). On the absolute continuity of the Blackwell measure. Journal of Statistical Physics 159, 158-171.

[KR11] I. Kolossváry, B. Ráth (2011). Multigraph limits and exchangeability. Acta Mathematica Hungarica 130, 1-34.

[KT11] I. Kolossváry, M. Telek (2011). Explicit Evaluation of ME(3) Membership. QUEST 2011: Fast Abstracts, CTIT Workshop Proceedings Series WP11-03, 11-12. 

 

Linkgyűjtemény.

Poszterek a témában: IHRG, RAN.

Szakmai önéletrajz

 

Hivatkozások listája.

[1] H. Amini, M. Lelarge (2015). The diameter of weighted random graphs. Ann. Appl. Probab. 3, 1686–1727.

[2] A.-L. Barabasi,  R. Albert (1999). Emergence of scaling in random networks. Science 286, 509-512.

[3] S. Bhamidi, R. van der Hofstad, G. Hooghiemstra (2010). First passage percolation on random graphs with finite mean degrees. Ann. Appl. Probab. 20(5), 1907-1965.

[4] S.Bhamidi, R. van der Hofstad, G. Hooghiemstra (2011). First passage percolation on the Erdős-Rényi random graph. Combinatorics, Probability and Computing 20, 683-707.

[5] B. Bollobás, S. Janson, O. Riordan (2007). The phase transition in inhomogeneous random graphs. Random Structures and Algorithms 31, 3-122.

[6] B. Bollobas, O. Riordan, J. Spencer, G. Tusnady (2001). The degree sequence of a scale-free random graph process. Random Structures and Algorithms 18, 279-290

[7] F. Chung, L. Lu (2003). The average distance in a random graph with given expected degrees. Internet Math. 1, 91–113.

[8] C. Cooper, A. Frieze, and R. Uehara (2014). The height of random k-trees and related branching processes. Random Struct. Alg. 45, 675-702.

[9] E. Ebrahimzadeh, L. Farczadi, P. Gao, A. Mehrabian, C. M. Sato, N. Wormald, J. Zung (2013). On the Longest Paths and the Diameter in Random Apollonian Networks. Electronic Notes in Discrete Mathematics 43, 355-365.

[10] P. Erdős, A. Rényi (1960). On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5, 17-61.

[11] C. D. Howard (2004). Models of first-passage percolation. In Probability on Discrete Structures, Springer, Berlin, pp. 125–173.

[12] S. Janson (1999). One, two and three times log n/n for paths in a complete graph with random weights. Combinatorics, Probability and Computing 8(4), 347-361.

[13] Z. Zhang, L. Rong, F. Comellas (2006). High-dimensional random Apollonian networks. Physica A: Statistical Mechanics and its Applications 364, 610-618.

[14] T. Zhou, G. Yan, B.-H. Wang (2005). Maximal planar networks with large clustering coefficient and power-law degree distribution. Phys. Rev. E 71, 046141.