George A. Olah Doctoral School of Chemistry and Chemical Technology 

Department of Inorganic and Analytical Chemistry

Supervisor: Dr. Csonka Gábor István

Application of Density Functionals for Organic and Biomolecules 

Introducing the research area

The aim of my doctoral research is to develop, test and apply theoretical methods based on electron density for the structure and weak interactions of organic and biomolecules. In my application, I present the current issues and solutions of density functional development for the description of weak interactions in complex compounds and chemical reactions. During my work, I managed to provide highly accurate solutions using time-efficient methods. My results are widely applicable for designing and modelling new complex interactions and reactions.

 

Brief introduction of the research place

My supervisor has many significant publications in the field of density functional theory and weak interactions [1–9]. In topics of density functional theory, our research group collaborates with the Center of Materials Theory of Temple University Philadelphia led by Prof. John P. Perdew. The joint results were published in journals with high impact factor and were outstandingly highly cited. Furthermore, we are currently contributing to the testing of MRCC quantum chemical software with Dr. Mihály Kállay, head of the Spectroscopy Laboratory of BUTE Department of Physical Chemistry and Materials Science.

 

History and context of the research

Ion channels and ion receptors

     Synthetic ion channels can be built in the cell membrane artificially, their properties can be modelled and designed using theoretical methods. The synthetic ion channels which are selective for a given ion potentially lead to a new family of single-molecule sensing technologies. Selectivity is based on the designed physicochemical interaction between the ion and the pi system. Similarly, selective cation or anion receptors can be engineered using methods of supramolecular chemistry. The accurate and fast calculation of anion-pi interactions [10], in contrast with the cation-pi interactions, has not been solved in the literature so far.

 

 

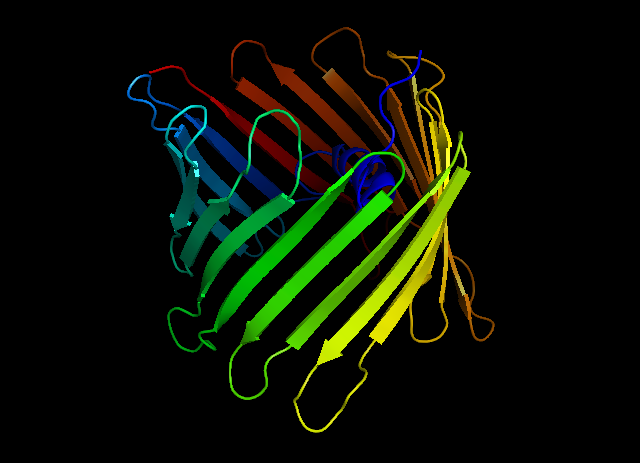
Human voltage-dependent non-selective anion channel (on the left) and modelling of the selective anion-pi interactions necessary for a selective anion channel or receptor (on the right)

 

Diels-Alder reactions

       Diels-Alder reactions are essential ring formation reactions, their discovery was rewarded by a Nobel Prize in Chemistry in 1950. These reactions become highlighted in theoretical chemistry because of the delocalization error of density functionals [11]. This originates in the misunderstanding that the loss of extended conjugation (delocalization in chemical sense) during the reaction would result in more localized electron density. However, the Diels-Alder reactions provide a great opportunity to test the intramolecular interactions because the non-bonded electron density overlaps formed in the mono-, bi- and tricyclic products make the calculations difficult. The accurate and fast calculation of Diels-Alder reaction energies has not been solved in the literature so far.

 

 

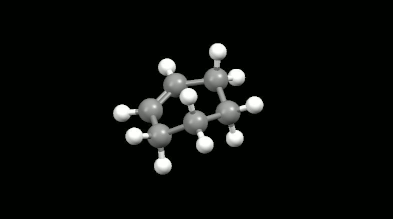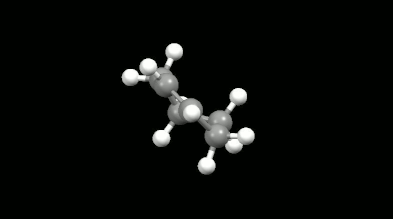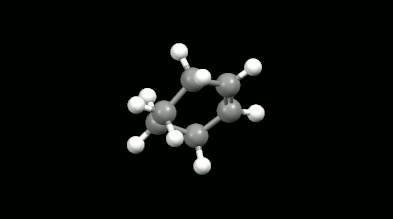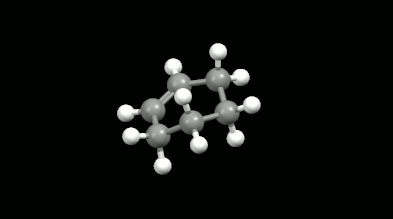
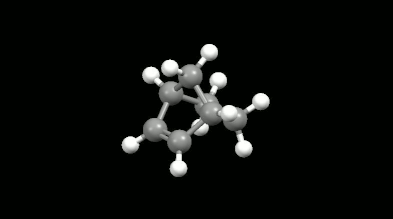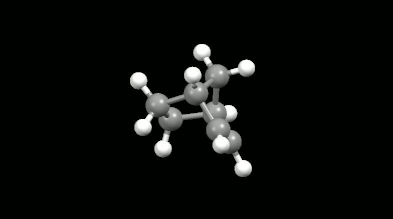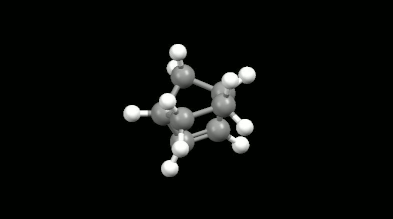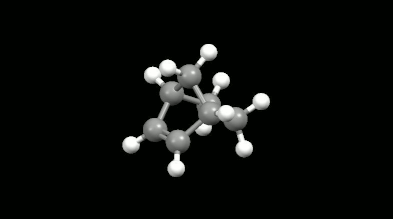
Ring-shaped and cagelike mono- and bicyclic products of Diels-Alder reactions

 

The research goals, open questions

Development of methods in computational chemistry

        Methods in computational chemistry are required to be accurate and fast. Accuracy means trueness and precision at the same time. The method is chemically accurate, if the error is at most 1 kcal mol-1 in the calculation of chemical systems. The speed can be interpreted by computational time for a system with given size, but the scaling of the computational time with the system size is also important for comparison. The method is efficient, if it is accurate and fast at the same time. The computational methods need to be tested, validated similarly to the experimental methods. The efficiency is determined using benchmark databases constructed based on the common problems of theoretical chemistry practice. The GMTKN30 database is one of such well-known databases, which tests the thermochemistry, kinetics and non-covalent interactions of compounds constituted by main group elements [12].

 

Calculation of weak interactions

        The strong covalent interactions result in more localized electron density, so the semi-local density functional methods can handle them better. Decreasing the strength of the interaction the electron density become more diffuse, thus the delocalization error of density functionals (many-electron self-interaction error) appears.  Moreover, fundamental problem is the description of the non-local nature of the long-range weak dispersion interactions with semi-local density functionals. It is difficult to solve the problem because the interaction and reaction energies can be fairly complex, and the delocalization and dispersion errors are often present at the same time.

 

Methods

Why density functional theory?

In theoretical chemistry, the physical and chemical properties of atoms and molecules can be calculated according to the approximate solutions of the Schrödinger equation (since exact solution is possible only for the simplest cases). Increasing the number of electrons, the wave function of the systems with chemical interest becomes untreatable, hence a different approach is needed. It is plausible using the three-dimensional electron density function instead of the multidimensional wave function. The idea of density functional theory is very powerful because we can treat our systems using one-electron eigenvalues equations, the Kohn-Sham equations [13]. The Kohn-Sham potential is constituted by the nuclear external potential, the average electronic repulsion Hartree potential, as well as the exchange and correlation potentials. The latter is unknown, however, in practice the exchange and correlation potentials are approximated together.

 

Density functional approximations

The hierarchy of density functional methods can be represented on the ‘Jacob’s ladder’ of density functional approximations according to Perdew [14]. In the original story, Jacob saw a ladder in his dream which reached up to the heaven, and the angels climbed up and down between the earth and heaven. The case is similar because, although the formulation of density functional theory is exact, the exact exchange-correlation functional exists only in the researchers’ dreams. The ladder represents well the hierarchy of approximations because from down to up the accuracy of the methods and also the computational time increase as the approximations take into account more and more information about the system. The researchers like the angels climb the ladder and choose a level of theory considering the difficulty of the problem.

 

Jacob’s ladder of density functional approximations

 

(LSDA: local spin density approximation, GGA: generalized gradient approximation, MGGA: meta-GGA, HGGA: hyper-GGA, RPA: random phase approximation)

 

Results

Accurate intermolecular interaction energies

The instance of binary or ternary anion-pi complexes demonstrates well the need for the accurate calculation of complex intermolecular interactions. In case of the binary complexes, I calculated highly accurate (DLPNO-CCSD(T)/CBS and LPNO-CEPA1/aug-cc-pVTZ) interaction energies. In comparison with these results, it was shown that the reference method (MP2/6-31++G(d,p) + CP correction) previously used in the literature [15] is hardly better than the Hartree-Fock method, thus it is not suitable to be a reference.

 

Possibilities for anion-pi interaction formation with respect to the pi-system

 

(Blue regions are electrostatically positive, so they can attract the negatively charged anions.)

 

On the anion-pi interactions, the performance of several methods on different levels which consider dispersion was determined. It was shows that only the RPA method can provide accurate anion-pi interaction energies among the density functional methods. By the ternary complexes, accurate RPA reference energies were calculated for the development of new density functionals and for further benchmarking.

 

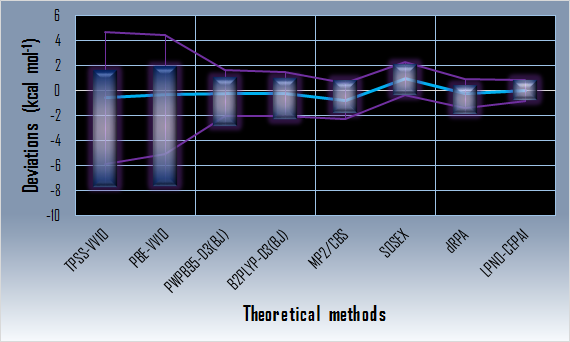
Calculated anion-pi interaction energy deviations from the reference

(applying ATZ basis set except for the MP2 method)

 

(Ranges of deviations are denoted with blue rectangles, the mean deviations are denoted with light blue line, the two corrected sample standard deviation band around the mean is denoted with purple lines.)

 

Accurate intramolecular interaction energies

The instance of Diels-Alder reactions, which lead to cyclic products, demonstrates well the need for the accurate calculation of the complex intramolecular interactions. In comparison with the reference energies (CCSD(T)/CBS) of the GMTKN30-DARC database [11, 12], the performance of several density functional methods were determined on different levels which consider dispersion. It was shown that only the RPA method can provide accurate Diels-Alder reaction energies among the density function methods.

 

 

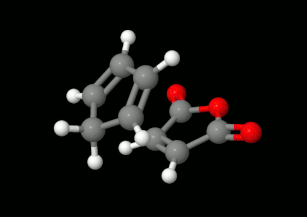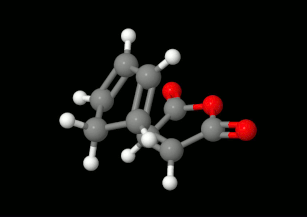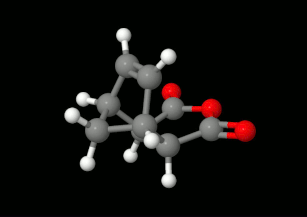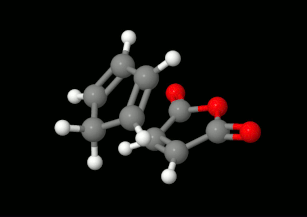
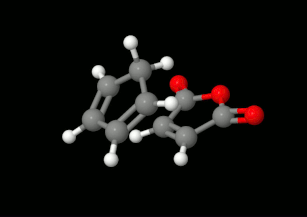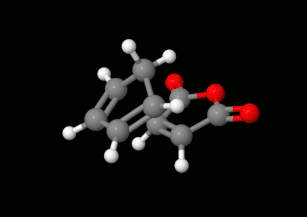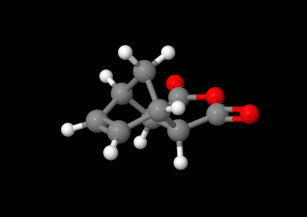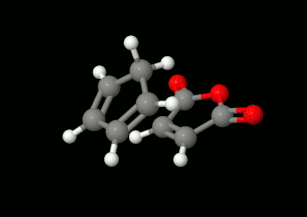
Modelling of Diels-Alder reactions: possibilities for formation of tricyclic product

 

(on the left: endo conformation, on the right: exo conformation)

 

It was also shown that increasing the exact exchange the energy of systems with more diffuse electron density deepens more, and since the reaction energies are shifted towards the exothermic direction overall, more diffuse electron density in the products results in more delocalized exchange-correlation hole in contrast to the earlier assumption in the literature.

 

Calculated Diels-Alder reaction energy deviations from the reference

 

(Ranges of deviations are denoted with red rectangles, the mean deviations are denoted with red line, the two corrected sample standard deviation band around the mean is denoted with yellow lines.)

 

New effective complete basis set extrapolation

Solving the slow convergence problem of the direct RPA correlation energy, I established a complete basis set extrapolation scheme which uses smaller basis sets and can reach the high accuracy of conventional extrapolation techniques [16] within more than one order of magnitude shorter time. The procedure is based on our finding that the correlation energy converges slower than the inverse cubic expression suggested in the literature and differently for molecules with different composition and structure.

 

 

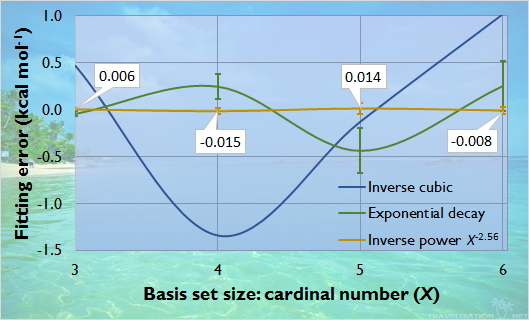
Convergence of direct RPA correlation energy with increasing basis set size approximated with different functions

 

(average fitting error for 65 hydrocarbon isomers, using aug-cc-pVXZ basis sets)

 

For 65 hydrocarbons (from the composition of CH4 to C6H6), the basis set convergence of the dRPA correlation energy was determined using correlation consistent aug-cc-pVXZ basis sets (X = T, Q, 5, 6). The exponent of the inverse power function was estimated individually with linear combination from the atomic contributions relatively to the total number of atoms within the molecule, or more accurately considering also the hybridization states, which carry structural information.

 

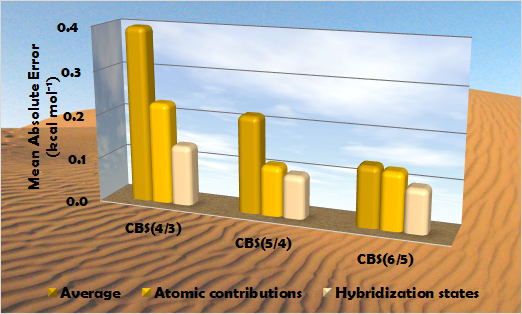
Error of complete basis set extrapolation techniques

 

(mean absolute error for 65 hydrocarbon isomers, using aug-cc-pVXZ basis sets)

 

New dual-hybrid RPA method

Furthermore, a new sort of dual-hybrid RPA method (dRPA75) was developed, which performs considerably well in several fields of molecular physical chemistry. It computes the dRPA correlation energy on PBE hybrid orbitals with 75% of exact exchange (which is beneficial to diminish the many-electron self-interaction error for organic molecules [17, 18]), and pair it with the hybrid exchange instead of the exact exchange energy. The performance of my method was determined compared to double hybrid functionals and other RPA methods  using databases which contain reaction energies, activation barriers and non-covalent interactions.

 

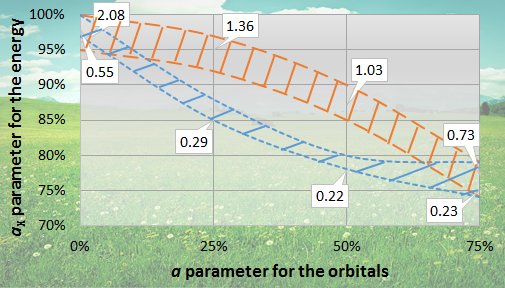
Parameter optimization for developing the dual-hybrid (dRPA75) functional

 

(The orange area with long dashed line borders is optimal for activation energies, the blue area with short dashed line borders is optimal for the reaction energies. The locally minimal mean absolute deviations in kcal mol-1 are noted.)

 

In contrast to the pairwise dispersion corrections, the new method can catch the non-atom-pairwise nature of non-covalent interactions. It is universally useful for all types of intra- and intermolecular interactions. Furthermore, it performs better for reaction energies than the double hybrid methods, and it is more accurate for hydrogen transfer barrier heights than the more expensive RPAX2 method [19].

 

Performance of the new dual-hybrid method (dRPA75) for reaction energies, barrier heights and weak interactions

 

Expected impact and further research

        My results are being published in the high-impact Journal of Chemical Theory and Computation (IF: 5.498). The detailed analysis and the highly accurate reference energies provided in our paper about the anion-pi interactions [O1] can form the basis for developing and testing new functionals. Our paper about the Diels-Alder reactions [O2] compares the potential ways to correct the delocalization and dispersion errors of density functionals. The complete basis set extrapolation technique of mine [O3] solves the problem of the slowly converging RPA correlation energy within more than one order of magnitude shorter time, therefore it enables the calculation of larger molecules. The dual-hybrid RPA method of mine [O4] performs exceedingly well on many fields of molecular physical chemistry, and it has been implemented in the MRCC quantum chemical software. I will continue to work on the efficiency and wider application of this method.

 

Publications, references, links

Publications:

[O1] Mezei, P. D.; Csonka, G. I.; Ruzsinszky, A.; Sun, J. J. Chem. Theory Comput. 2015, 11, 360–371.

[O2] Mezei, P. D.; Csonka, G. I.; Kállay, M. J. Chem. Theory Comput. 2015, 11, 2879–2888.

[O3] Mezei, P. D.; Csonka, G. I.; Ruzsinszky, A. J. Chem. Theory Comput. 2015 just accepted, published online. ct–2015–00269g

[O4] Mezei, P. D.; Csonka, G. I.; Ruzsinszky, A.; Kállay, M. J. Chem. Theory Comput. 2015 under revision. ct–2015–00420z

 

Links:

Kohn’s Nobel lecture on the development of density functional theory

Interview with Walter Kohn by Tony Cheetham and John Perdew

Perspective: fifty years of density functional theory in chemical physics

Challenges for Density Functional Theory by Cohen, Mori-Sánchez and Yang

Insights into Current Limitations of Density Functional Theory by Cohen, Mori-Sánchez and Yang

 

References:

[1] Perdew, J.; Ruzsinszky, A.; Csonka, G. I.; Vydrov, O.; Scuseria, G.; Constantin, L.; Zhou, X.; Burke, K. Phys. Rev. Lett. 2008, 100, 136406.

[2] Ruzsinszky, A.; Csonka, G. I.; Scuseria, G. E. J. Chem. Theory Comput. 2009, 5, 763–769.

[3] Perdew, J. P.; Ruzsinszky, A.; Csonka, G. I.; Constantin, L. A.; Sun, J. Phys. Rev. Lett. 2009, 103, 026403.

[4] Ruzsinszky, A.; Sun, J.; Xiao, B.; Csonka, G. I. J. Chem. Theory Comput. 2012, 8, 2078–2087.

[5] Perdew, J. P.; Ruzsinszky, A.; Tao, J.; Staroverov, V. N.; Scuseria, G. E.; Csonka, G. I. J. Chem. Phys. 2005, 123, 62201.

[6] Steinmann, S. N.; Csonka, G. I.; Corminboeuf, C. J. Chem. Theory Comput. 2009, 5, 2950–2958.

[7] Ruzsinszky, A.; Perdew, J. P.; Csonka, G. I. J. Chem. Theory Comput. 2010, 6, 127–134.

[8] Ruzsinszky, A.; Perdew, J. P.; Csonka, G. I. J. Chem. Phys. 2011, 134, 114110.

[9] Csonka, G. I.; French, A. D.; Johnson, G. P.; Stortz, C. A. J. Chem. Theory Comput. 2009, 5, 679–692.

[10] Schottel, B. L.; Chifotides, H. T.; Dunbar, K. R. Chem. Soc. Rev. 2008, 37, 68–83.

[11] Johnson, E. R.; Mori-Sánchez, P.; Cohen, A. J.; Yang, W. J. Chem. Phys. 2008, 129, 204112.

[12] Goerigk, L.; Grimme, S. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688.

[13] Kohn, W.; Sham, L. J. Phys. Rev. 1965, 140, A1133–A1138.

[14] Perdew, J. P.; Schmidt, K. AIP Conf. Proc. 2001, 577, 1–20.

[15] Garau, C.; Frontera, A.; Quiñonero, D.; Russo, N.; Deya, P. M. J. Chem. Theory Comput. 2011, 7, 3012–3018.

[16] Fabiano, E.; Della Sala, F. Theor. Chem. Acc. 2012, 131, 1278.

[17] Sai, N.; Barbara, P. F.; Leung, K. Phys. Rev. Lett. 2011, 106, 226403.

[18] Atalla, V.; Yoon, M.; Caruso, F.; Rinke, P.; Scheffler, M. Phys. Rev. B – Condens. Matter Mater. Phys. 2013, 88, 1–8.

[19] Heßelmann, A. Phys. Rev. A 2012, 85, 012517.