Pál Csonka Doctoral School 

BME Faculty of Architecture, Department of Mechanics, Materials & Structures

Supervisor: Dr. Sipos András Árpád

Wrinkling Patterns of Thin Films

Introducing the research area

The investigation of the buckling phenomenon of thin films, called wrinkling and the shape of the emerging wrinkles play a key role in many practical problems. During the design of solar sails, airbags, membrane structures and web transporting rolls the reduction or prevention of wrinkling is an important factor.

 

Fig. 1: Wrinkling at the failure of a membrane structure (physical model)

 

As the field is relatively new and there are only a few experimental results in the literature, the theoretical models used to describe wrinkling are highly debated among the researchers. The aim of this research is to model various problems related to the wrinkling of thin films with the Föppl-von Kármán plate theory and its variant extended to finite membrane strains, to compare experimental results to numerical computations and to clarify conditions of their applicability.

 

Brief introduction of the research place

The colorful profile of the Department of Mechanics, Materials and Structures is defined by various theoretical, experimental and structural engineering research projects. Our researchers and educators work on the design of load bearing structures made of different materials; they investigate brick and stone structures, buckling phenomena of thin shells and films, shape memory alloys, morphology of pebbles and stability problems of colliding bodies.

 

History and context of the research

Wrinkling is a buckling phenomenon caused by compressive stress in ultrathin plates, the so-called films. Thin films have a rich morphology; besides wrinkling we can find crumpling, folding and delamination, collectively described as pattern formation on the surface. Although Timoshenko in 1936 discussed the buckling of thin plates in his book, the wrinkling of thin films became a vigorously researched topic only after the appearance of a Nature paper of Cerda, Ravi-Chandar and Mahadevan in 2002. They investigated thin, stretched, rectangular films clamped at two ends. The Poisson's effect causes compressive forces in the film, which can lead to wrinkling.

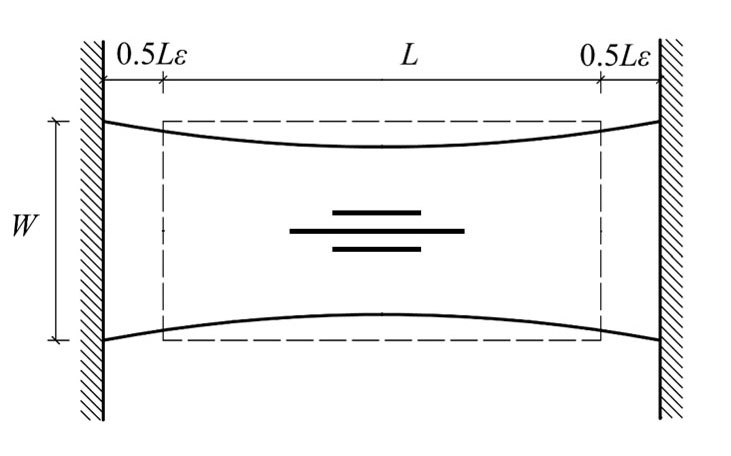
Fig. 2: Wrinkling of a stretched, clamped, rectangular film

 

One of the mainly used theories to model the phenomenon is the Föppl-von Kármán plate theory of thin films, which assumes finite deflections but small strains. However, it was used in many cases to model problems with properties contradictory to the assumptions of the theory. Healey in 2013 extended the model to finite strains and predicted the disappearance of wrinkles above a critical stretch. On top of that, his work suggested that wrinkles appear only for a certain range of aspect ratios.

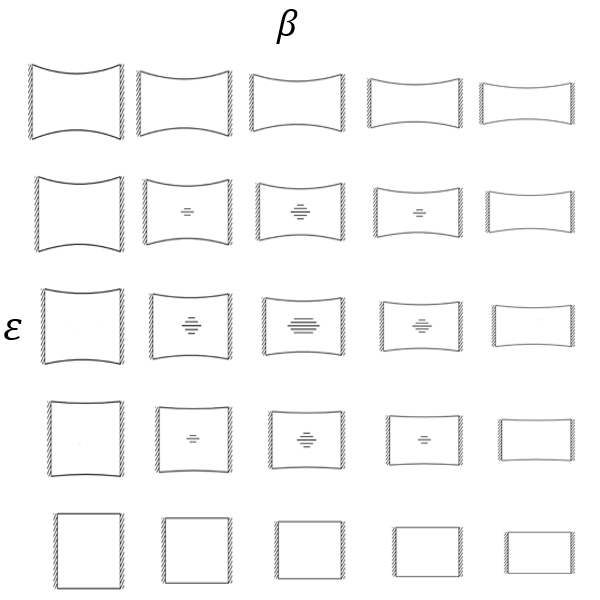
Fig. 3:  Predictions of the finite strain theory (: aspect ratio, : stretch)

 

Due to the lack of experiments in the literature these predictions were still to be experimentally verified. Finding a sufficiently thin and elastic material to carry out the experiments is a difficult task. Polymers are flexible and available in the appropriate thickness, however, their material properties have a great effect on the wrinkling phenomenon making it complicated to compare the experimental results with the computations.

 

Research goals, open questions

One of the main goals of this research is to carry out a comprehensive experimental investigation using a material closer to linear elasticity than materials used in the literature. A systematic investigation of stretched rectangular films having different aspect ratios is required to verify the predictions of the finite strain theory. These experiments can point to the importance of the extension to finite strains. Since the Föppl-von Kármán plate theory is based on the assumption of homogeneous, isotropic, linear elastic material, it is important to measure the properties of the chosen material and to determine how they affect the wrinkling phenomenon.

 

During the experiments, it was observed that under cyclic loading, films with certain aspect ratios do not wrinkle under the first loading but become wrinkled during the unloading and the following cycles. One part of the research is to find an explanation for this phenomenon.

 

To compare the experimental results with computations, a numerical algorithm was needed, which is capable of using both theories. The Euler-Lagrange equations of the Föppl-von Kármán plate theory is a system of fourth-order, nonlinear partial differential equations. The development of a finite element method based numerical continuation algorithm was aimed which enables us to incorporate more complicated material models and investigate other geometries.

 

However, in real life situations wrinkling is not restricted to planar problems; therefore the extension of the model to surfaces embedded in three dimensions is necessary. The models available in literature usually assume that the parameterization of the surface is known and the equations are based on a simpler form of the equations formulated in terms of the Airy stress function. As there is no Airy stress function in case of the finite strain model, we aimed at creating a model for the computation of three-dimensional surfaces for both theories and arbitrary (but sufficiently smooth) geometries. It is to be investigated, how the curvature of the surface and the incorporation of finite strains affect the wrinkling behavior.

 

Methodology

During the experiments, at first we examined polyethylene films and verified qualitatively the disappearance of wrinkles predicted by the finite strain theory [3]. Then we loaded 50 mm long, 20 micrometer thick polyurethane films having different widths with an extension-controlled device and determined by inspection the critical stretch where the wrinkles disappear in case of a given aspect ratio [2].

 

 

Fig. 4: Experimental results for different aspect ratios and stretch

 

Then the material properties of the films were determined using the materials testing machine of our Czakó Adolf laboratory. The stress-strain diagrams of the film in longitudinal, transversal and 45° directions were determined. It was observed that although the pre-stressed films are nearly linearly elastic, the preloading causes orthotropy. We implemented an orthotropic material model to investigate how the lack of isotropy affects wrinkling.

 

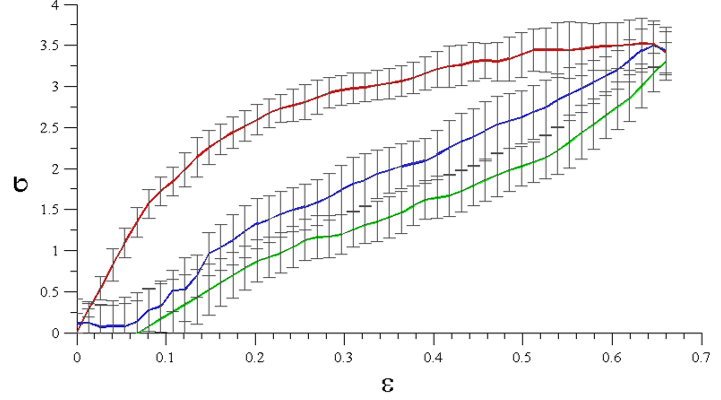
Fig. 5.  Stress-strain diagram in the longitudinal direction (red: pre-stress, green: unloading, blue: reloading)

 

To be able to model the whole process, the implementation of a hyperelastic model such as the Mooney-Rivlin material model and a damage model was necessary. The Mooney-Rivlin material model is usually used to model polyurethane films. The so-called Mullins-effect was appropriate to explain the behavior observed during cyclic loading. The idea behind the Mullins-effect is that the damage is considered by damage fields depending on the previously reached maximal extension and it assumes the damage occurring only on the unloading paths.

 

Fig. 6: Cyclic loading of polyurethane films

 

 

Fig. 7: The Mullins-effect (A: loading path, B: unloading paths)

 

The numerical implementation of the models was carried out in Matlab using rectangular finite elements with C1 continuity. The algorithm was able to compute the wrinkling of stretched rectangular films, but to extend the model with more complex material models and to investigate other geometries a more general implementation was needed. Our numerical continuation algorithm is written in C++ and based on the open source finite element library FEniCS. The advantage of using FEniCS is that it handles the equations and geometries separately, that allows easy implementation of new material laws as well as geometries.

The software solves the weak form of the equations by means of the Discontinuous Galerkin method, which enforces the continuity of the derivatives only weakly on the element boundaries enabling us to use the standard Lagrangian function spaces. The algorithm determines the bifurcation points by computing the sign of eigenvalue of the Jacobian matrix having the smallest magnitude. These bifurcation points are related to the appearance and disappearance of wrinkles. 

 

Fig 8: Buckling shape of an axially compressed cylindrical shell

 

There are numerous models extending the Föppl-von Kármán theory to curved surfaces. However, they are usually restricted to specific geometries or based on a simpler form of the equations formulated in terms of the Airy stress function. It can be shown that in case of the finite strain model no Airy stress function exists. As in FEniCS the derivatives are automatically computed in the tangent space for curved surfaces, it is simple to extend our model to curved surfaces. Nevertheless, the curvature of the surface has to be incorporated in the membrane strain energy. The curvature is known a priori or it can be approximated from the finite element nodes.

 

Results

The incorporation of the orthotropy in the model resulted in good agreement between the computations based on the finite strain theory and the experiments carried out on pre-stressed polyurethane films. The results verify the need for the finite strain extension. It was also proved by the experiments, that wrinkling occurs only in case of certain aspect ratios.

 

The effect of the orthotropy on the extent of the closed region containing wrinkled configurations (on the aspect ratio - stretch diagram) was numerically examined. It was revealed that for a given film thickness, the larger the orthotropy the greater the region. Nevertheless, in the literature the polymers used in the experiments are usually assumed to be isotropic, therefore it is important to emphasize the effect of orthotropy.

 

The dash-dotted line on Fig. 8. bounds the region prone to wrinkling. Outside this border, no compressive stress occurs in the film. It was derived that the curve has a limit, suggesting that there exists a critical stretch where the wrinkles disappear independently of the thickness.

 

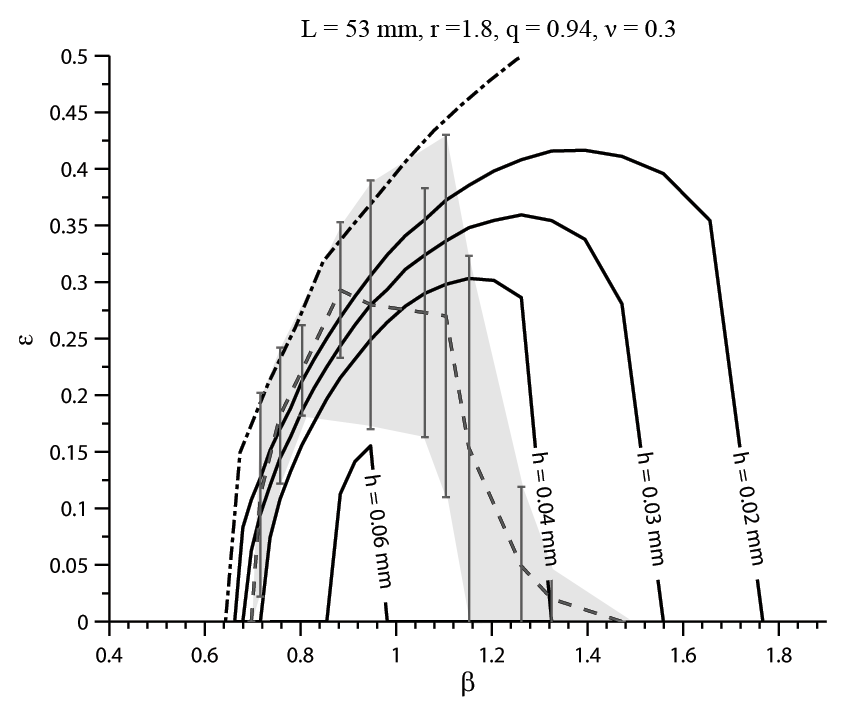
Fig. 9: Comparison of the critical stretch observed on pre-stressed polyurethane films with computational results (r,q: parameters of orthotropy, : Poisson’s ratio, h: thickness)

 

Consideration of the Mullins-effect enabled us to model the whole cyclic loading process and led to good agreements between the experiments and the computations. Pre-stress causes damage in the structure of the polymer changing the material properties of the film which explains the behavior observable on Fig. 6. As far as the maximal extension of the films is not increased, the material behavior is almost linear elastic.

 

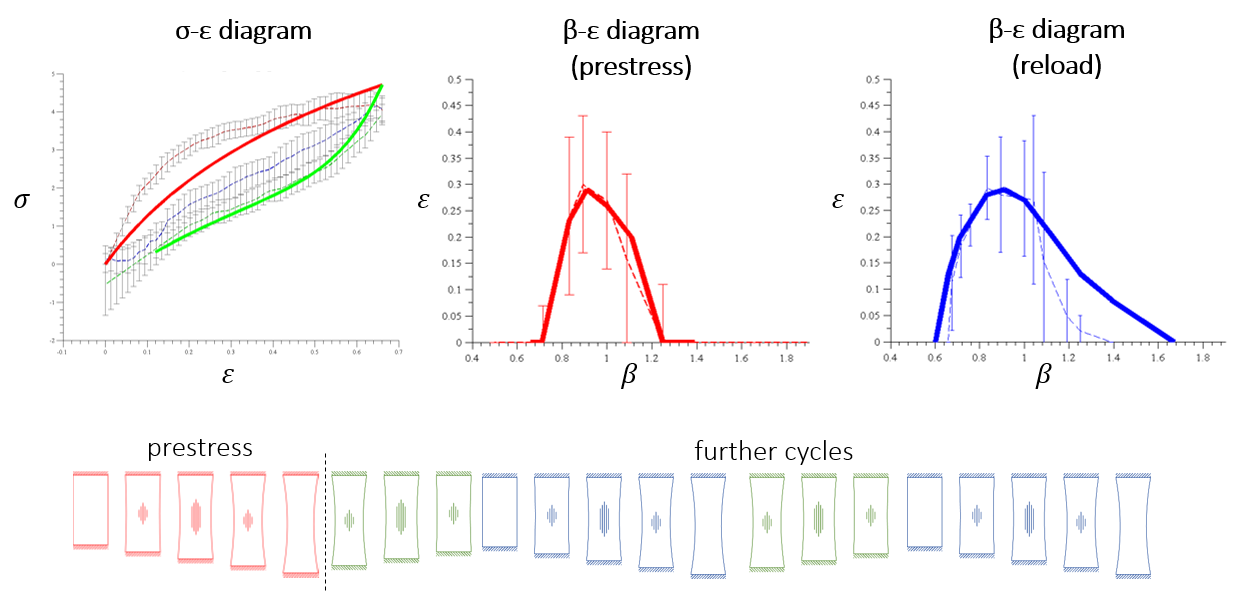
Fig. 10: Modeling the cyclic loading using the Mullins-effect

 

 

To validate our model extended to curved surfaces, we computed the critical load for axially compressed cylindrical shells and compared it to analytical results. Then the effect of curvature was investigated on clamped, stretched cylindrical shells. It was revealed that by increasing the curvature wrinkles can be removed from the surfaces. Moreover, there exists a critical stretch above which no wrinkles appear independently of the applied stretch.

 

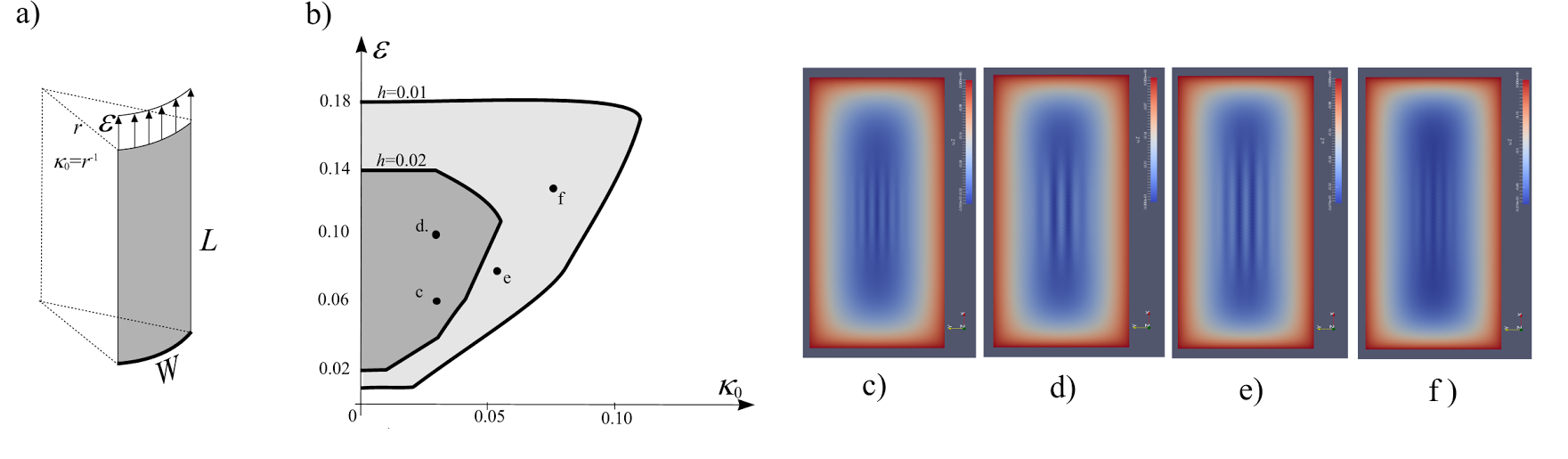
Fig. 11. The effect of the initial curvature on the wrinkling behavior

 

 

Finally, we examined the wrinkling of cylinders loaded simultaneously axially and laterally. Internal pressure causes no wrinkling, but stretch causes wrinkling in case of external pressure. There is a critical stretch, where the wrinkles disappear. However, the original Föppl-von Kármán model overestimates the stability boundary.

 

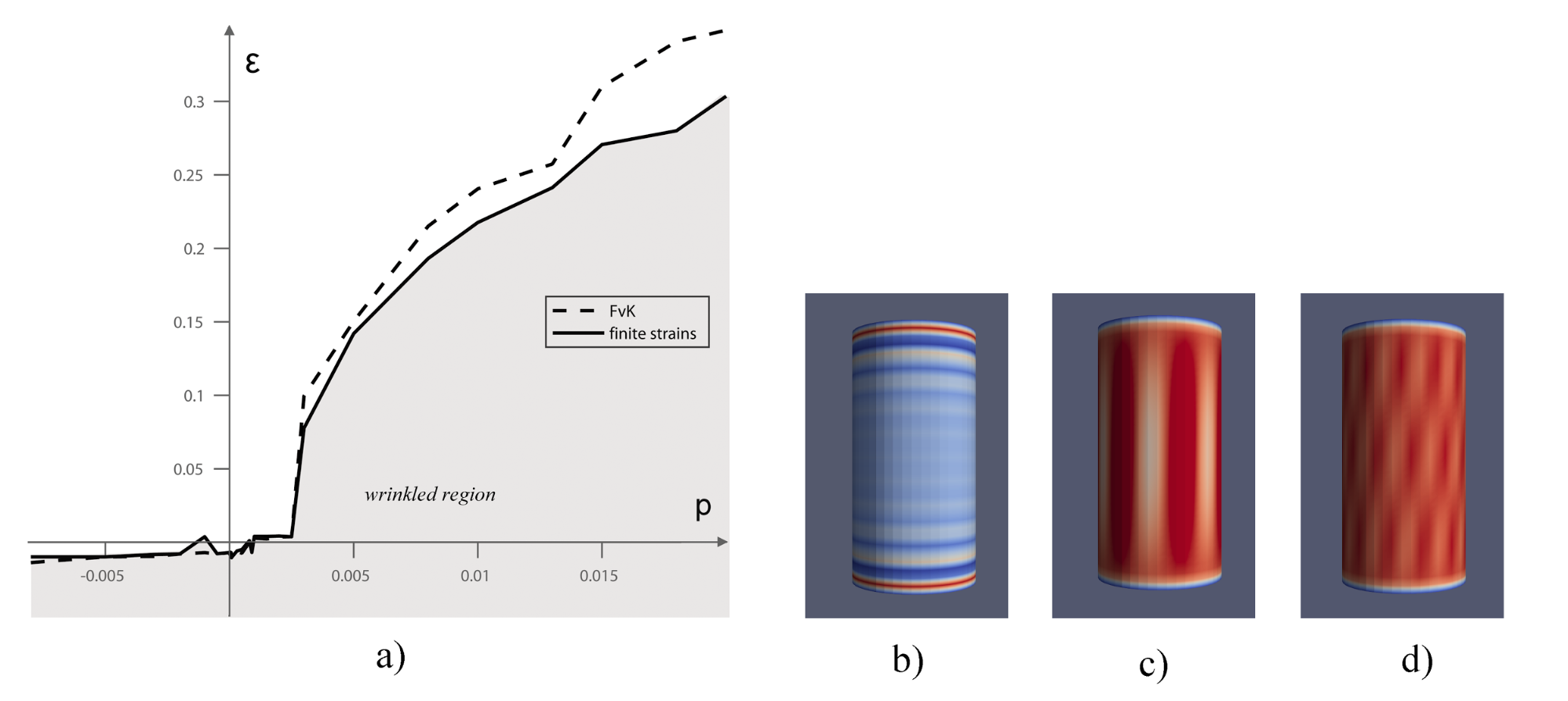
Fig. 12: Simultaneous axial and lateral loading of simply supported cylindrical shells

 

Further research

In the future, we plan to examine problems where the finite strain extension is inevitable to understand the emerging wrinkling patterns, but the experiments are difficult to carry out (for example in case Möbius-strips). From the practical point of view, an obvious extension is to work out further strategies to remove or avoid wrinkles, which is an emerging topic in the literature. From the theoretical point of view, the number of wrinkles is still an often debated, open question in case of stretched rectangular films. Nevertheless, these results contribute to the clarification of the applicability of the theories used to model wrinkling, and also underlined the important role that material properties play in the evaluation of these experiments.

 

Publications, references, links

Publications.

[F1] E. Fehér, A. Á. Sipos (2017), Wrinkling patterns of thin films under finite membrane strain, 9th European Nonlinear Dynamics Conference. Budapest, Hungary, 2017.06.25–30. p. 1-7. ISBN 978-963-12-9168-1

[F2] A. Á. Sipos, E. Fehér (2016), Disappearance of stretch-induced wrinkles of thin sheets: a study of orthotropic films, International Journal of Solids and Structures 97-98: pp. 275–283.

[F3] E. Fehér, A. Á. Sipos (2014), Wrinkling of stretched, thin sheets: occurrence and disappearance of the wrinkling pattern. Építés-Építészettudomány 42: 23–42. (in Hungarian)

[F4] E. Fehér, D. Hegyi, M. Halász, P. Tamás (2011), Wrinkling at the failure of membrane structures, International Symposium on Innovative Technologies and Design. Budapest, Hungary, 2011.11.21–22. pp. 1-10.

 

Talks.

[F5] E. Fehér, A. Á. Sipos (2016), Arclength continuation in FEniCS and its application to the study of wrinkling of ultrathin films, FEniCS’16 Workshop, Oslo, Norway, 2016.05.19.

 

Links.

http://www.szt.bme.hu/

https://fenicsproject.org

 

References.

[R1] Healey, T.J., Li, Q., Cheng, R.B., 2013. Wrinkling behaviour of highly stretched rectangular elastic films via parametric global bifurcation. J. Nonlinear Sci.23:777–805

[R2] Logg A., Mardal K-A., Wells G. N. Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book, Springer-Verlag Berlin Heidelberg, 84, 2012.

[R3] Timoshenko S.P., Gere J. M., 1961. Theory of elastic stability. McGraw-Hill Book Company, Inc., New York.

[R4] Karman T., Tsien H. S., 1941. The buckling of thin cylinders under axial compression and bending. Journ. Aero. Sci.8, No. 8 p. 303.

[R5] Cerda E., Mahadevan L., 2003. Geometry and physics of wrinkling. Phys. Rev. Lett. 90, 1–4.

[R6] Cerda E., Ravi-Chandar K., Mahadevan L., 2002. Wrinkling of an elastic sheet under tension. Nature 419, 579–580.

[R7] Davidovitch B., Schroll R.D., Vella D., Add-Bedia M., Cerda E., 2011. Prototypical model for tensional wrinkling in thin sheets. PNAS 108 (45), 18227–18232.

[R8] Friedl N., Rammerstorfer F., Fischer F., 2000. Buckling of stretched strips. Comput. Struct. 78, 185–190.

[R9] Donnell L.H., 1933. Stability of thin-walled tubes under torsion. NACA Rep. 479.

[R10] Rivière B., 2008. Discontinuous Galerkin Methods for Solving Elliptic and Parabolic Equations: Theory and Implementation. SIAM Frontiers in Applied Mathematics