|
|
BMe Research Grant |
|
Doctoral School of Electrical Engineering
BME-VIK, Department of Electric Power Engineering
Supervisor: Dr. Tamus Zoltán Ádám
Cost Optimization of Power Transformers’ Insulation Systems
Introducing the research area
Design of power transformers is a complex multidisciplinary task where numerous mechanical, thermal and electrical constraints should be considered simultaneously [1,2]. This task belongs to the most general branch of mathematical optimization problems. Therefore, the design process of power transformers is generally split into more phases. My research deals with the first design phase called preliminary design phase the purpose of which is to determine the key design parameters for the cost optimal design according to the requirements (Fig 1) [3,4] .

Fig. 1. Calculating the optimal key design parameters in the preliminary design process.
Brief introduction of the research place
The Department of Electric Power Engineering was established in 1893 by Károly Zipernowsky, one of the inventors of the closed core transformers. This was the first electrical engineering department of Budapest University of Technology and Economics. The mission of the department is to be an active partner of the industry by educating skillful electrical engineers, organizing international conferences, postgraduate courses, and trainings and carrying out research and development projects. In accordance with that we are in an active cooperation with numerous universities in Europe and overseas, as well.
History and context of the research
Determination of the key design parameters of the cost-optimal design of a power transformer in a given economic environment is a complex task belonging to the most general branch of mathematical optimization problems. To simplify the process, the design procedure is usually divided into three phases [3]:
● The preliminary design stage, intending to create a proposition, a design study, and the start of a requisition. The outputs of this step are called the key design parameters.
● The final design is the refinement of the preliminary design. Its output is the final design engineering record and the drafting and manufacturing instructions.
● Check of the final design.
My research topic deals with the optimization problems of the preliminary design. The main difficulty of this phase is to find the key design parameters of a both technically and financially competitive transformer design in a very short time. The brute force solution of this task has high calculation cost. It has already been demonstrated in [3] that even an ideal case with three constraints has approximately 100 000 cases to choose from.
The fact that the first analytical methods for this problem were discovered only a decade after the invention of the closed core transformers shows importance of the topic. These optimization methods contain many simplifications and technology-based assumptions restricting their application to special cases. Applying these methods beyond these simple cases can lead to erroneous design directives. From the 50’s, with the advent of computer age and the development of numerical methods key design parameters can be determined. Wide range of different techniques are available from simple iteration through complex numerical methods to artificial intelligence to find the optimal solution as fast as possible [7,8].
These preliminary design methods might have different objective functions e.g. manufacturing cost minimization, total mass minimization, outline volume minimization, and efficiency maximization. My research is about the minimization of the total cost of ownership consisting of the manufacturing cost and the operating cost by the capitalization factors [7]. The need for the optimization for the total cost of ownership has already occurred at the beginning of the 20th century. For instance, Ganz, the company pioneering the power transformer production, manufactured transformers with different core and copper mass ratio for water and steam turbines according to the different utilization factors. The modern methods are more accurate in terms of taking more factors into account [9, 10].
The research goals, open questions
Determining the cost-optimal key design parameters of power transformers it’s a part of the most general mathematical optimization problems. Due to the complexity of the task many simplified methods were published from time to time leading to erroneous design methods. The determination of the key design parameters of a power transformer is based on the volume and mass ratio of the core and windings. Hence, these simplified models are usually taking only the core and windings (“active part”) into account neglecting the insulation and outer cooling system. My investigations concentrate on the effects of these simplifications on the calculated key-design parameter values.
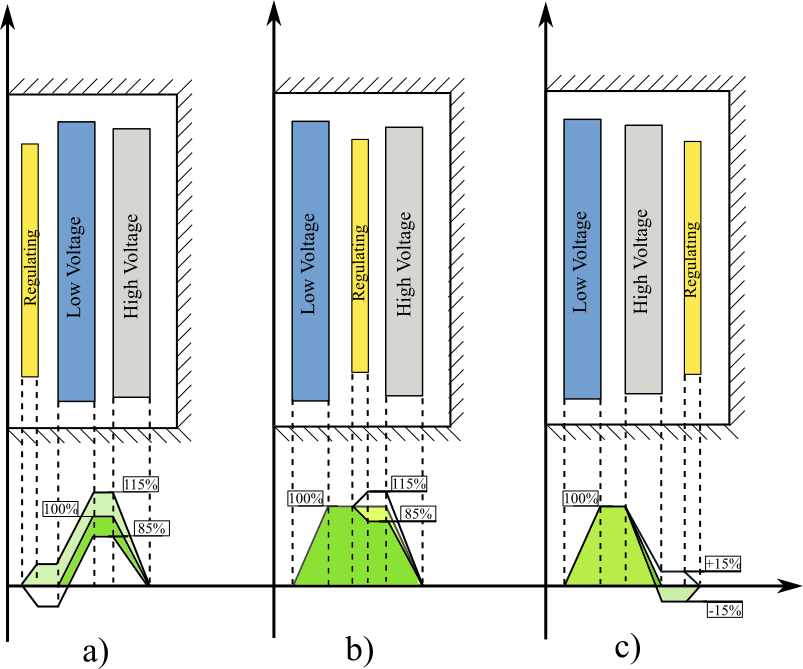
Fig. 2. The effect of the different regulating winding positions on the excitation curve..
Methods
The starting point of my research was a transformer optimization program based on geometric programming [1, 12]. Thanks to the modern solvers, such a geometric programming problem can be solved accurately in a very short time even using a normal PC [11]. This method also guarantees that the global optimum will be found. However, this method gave slightly erroneous results in the case of core-form power transformers: higher windings and higher working window height than the more precise method suggested. It’s a common belief that this difference is caused by the simplification of the effects of the regulating windings and the insulation and cooling system. Yet, I managed to prove that the deviation in the case of core-form power transformers is caused by the fact that the short-circuit impedance cannot be expressed in required posynomial form. To solve this problem, a metaheuristic algorithm is introduced by the combination of geometrical programming and branch and bound algorithms which is able to calculate the accurate short circuit impedance in a fast and accurate way. The method has been compared to other methods proving it efficient and useful. The method has also been validated by FEM [14]. With an extension of this method the connection between the value of the optimal key design parameters and the type and arrangement of the regulating windings (via the short-circuit impedance) and outer cooling.
Results
The metaheuristic model was extended with new parameters and a thermal model in order to study the effects of the mass and cost of the insulation and cooling system for natural oil flow (ONAN/ONAF) cooled transformers. With this model I examined the effect of the consideration of the outer cooling system on the key design parameters of the power transformer. I have found, in agreement with experience, that case of high capitalization cost, the effect of the cooling cost consideration is not significant. On the other hand, when the capitalization factors are small and the optimal transformer design has relatively large losses, the consideration of the cooling system has a significant effect on the optimal turn voltage and the core and copper mass ratio.
The built-in power of the autotransformers is smaller than their rated power, therefore in case of a cost-optimal design the regulating winding is located between the core and the inner winding or between the two main windings, not after the outer winding when it has the smallest impact on the short circuit impedance. The extended metaheuristic algorithm can calculate the short circuit impedance in the different physical locations of the regulating winding positions, thus the key design parameters of an autotransformer can be determined.
The impact of the tap-changing method selection on the key design parameters of the core-form transformers has been examined with another extension of metaheuristic optimization method. The main advantage of the reversing tap-changing arrangement is its capability to cope with large number of turns without the need of extra regulating winding and insulation distance. Therefore, it can decrease the manufacturing costs compared to a coarse-fine or a linear arrangement. Aside from the further advantages of the coarse-fine regulation: smoother short-circuit impedance change in the full regulation range and cheaper cooling system [13], I have demonstrated that the coarse-fine regulated transformer is cheaper than the reversing arrangement above a short circuit impedance value in the given economic environment.
Expected impact and further research
The industrial use of the above algorithms has been continuous since their development. An optimization code based on the above metaheuristic algorithm has been used by the High Voltage Solutions kft. and their partners.
The non-biodegradable mineral oil based transformer dielectric liquids are highly environment polluting. There is a tendency in our days to replace these oils with silicon and ester-based fluids. These materials have similar dielectric properties but different price, viscosity, thermal and ageing properties than the conventional transformer oils. With the extension of the metaheuristic algorithm the effect of these new environment friendly dielectrics on the total cost of ownership and on the key design parameters of the transformer can be investigated.
Publications, references, links
(J1) T. Orosz ,A., Sleisz and Z. A., Tamus. "Metaheuristic optimization preliminary design process of core-form autotransformers," IEEE Transaction on Magnetics, vol. 52 no. 4, April, 2016 (IF: 1.28)
(J2) T. Orosz, B. Borbély, Z. Á. Tamus,", Performance Comparison of Multi Design Method and Meta-Heuristic Methods for Optimal Preliminary Design of Core-Form Power Transformers," Periodica Polytechnica Electrical Engineering and Computer Science, vol 61, no. 1, 2017
(J3) T. Orosz and Z. Á. Tamus. "Impact of the Cooling Equipment on the Key Design Parameters of a Core-Form Power Transformer." Journal of Electrical Engineering, vol. 67 no. 6, pp. 399–406, 2016. (IF: 0.498)
(J4) T. Orosz, P. M. Sőrés, D. Raisz, Z. Á. Tamus, "Analysis of the Green Power Transition on Optimal Power
Transformer Design," Periodica Polytechnica Electrical Engineering and Computer Science, vol. 59 no. 3, pp. 125-131., 2015.
(J5) T. Orosz, G. Kleizer, T. Iváncsy, Z. Á. Tamus, "Comparison of Methods for Calculation of Core-Form Power Transformer’s Core Temperature Rise," Periodica Polytechnica Electrical Engineering and Computer Science, vol. 60, no. 2, pp. 88-95., 2016.
(J6) T. Orosz, T. Nagy, Z. A. Tamus, "A Generalized Geometric Programming Sub-problem of Transformer Design Optimization", "Technical Innovation of Smart Systems", Springer, pp. 373-381, 2017
(J7) T. Orosz and Z. Á. Tamus, "Impact of the Short Circuit Impedance and the Tap Changing Method Selection on the Key-design Parameters of Core-form Power Transformers." Springer, Electrical Engineering [minor revision] (IF: 0.662)
(C1) T. Orosz, Á. Sleisz, I. Vajda, "Core-Form Transformer Design Optimization with Branch and Bound Search and Geometric Programming", in 2014 55th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 2014.
(C2) P. Sorés, T. Orosz, I. Vajda, "Lifetime Cost Sensitivity Assessment in Optimal Core-form Power Transformer Design", in: 9th International Conference on Deregulated Electrical Market Issues in South Eastern Europe, Nicosia, Cyprus, 2014.
(C3) T. Orosz, I. Vajda, "Power Transformer Design Optimization with Geometric Programming," in Topical Problems in the Field of Electrical and Power Engineering: Doctoral School of Energy and Geotechnology II., Parnu, Estonia, 2014.
(C4) T. Orosz, I. Vajda, "Költségoptimális nagytranszformátor tervezés Geometriai Programozás segítségével", in 29. Kandó Konferencia = 29th Kandó Conference, Budapest, Hungary, 2013.
References:
[1] R. M. Del Vecchio, B. Poulin, P. T. Feghali, D. M. Shah, and R. Ahuja, Transformer design principles: with applications to core-form power transformers. CRC press, 2001.
[2] H. M. Ryan, High voltage engineering and testing 3rd Edition. No. 32, IET, 2013.
[3] P. Abetti, W. Cuthbertson, and S. Williams, „Philosophy of applying digital computers to the design of electric apparatus,” American Institute of Electrical Engineers, Part I: Communication and Electronics, Transactions of the, vol. 77, no. 3, pp. 367–379, 1958.
[4] Kiss L., Karsai K., Kerényi D., Nagytranszformátorok, Műszaki Könyvkiadó, 1973.
[5] G. Kapp, Transformatoren für Wechselstrom und Drehstrom [Transformers for Single and Multiphase Currents: A Treatise on Their Theory, Construction, and Use]. Charleston SC, United States: Nabu Press, 2012 [1900]. Originally published in: 1900.
[6] G. Ujházy, Eroátviteli transzformátorok gépi számításának kérdései [Application of Computers for Power Transformer Design]. PhD thesis, Budapest University of Technology and Economics, 1969. [In Hungarian].
[7] E. I. Amoiralis, M. A. Tsili, and A. G. Kladas, “Transformer design and optimization: a literature survey,” Power Delivery, IEEE Transactions on, vol. 24, no. 4, pp. 1999–2024, 2009.
[8] P. S. Georgilakis, Spotlight on modern transformer design. Springer Science & Business Media, 2009.
[9] S. Corhodzic and A. Kalam, „Assessment of distribution transformers using loss capitalization formulae,” Journal of Electrical and Electronics Engineering Australia, vol. 20, no. 1, pp. 43–48, 2000.
[10] „IEEE loss evaluation guide for power transformers and reactors,” 1992.
[11] S. Boyd and L. Vandenberghe, Convex optimization. Cambridge university press, 2004.
[12] R. A. Jabr, „Application of geometric programming to transformer design,” Magnetics, IEEE Transactions on, vol. 41, no. 11, pp. 4261–4269, 2005.
[13] A. White, „Tapchanging-the transformer designer’s perspective,” in Developments On-Load Tapchangers: Current Experience and Future, IEE European Seminar on, pp. 4–1, IET, 1995.
[14] O. W. Andersen, „Transformer leakage flux program based on the finite element method,” IEEE Transactions on Power Apparatus and Systems, vol. PAS-92, pp. 682–689, March 1973.
