Villamosmérnöki Tudományok  Doktori Iskola 

BME VIK, Méréstechnika és Információs Rendszerek Tanszék

Témavezető: Dr. Kollár István

Analóg-digitális átalakítók minősítésének támogatása - egy pontos és költséghatékony eljárás a numerikus pontatlanságok csökkentésére

A kutatási téma néhány soros bemutatása

A számítógépek elterjedésével a jelfeldolgozási feladatok túlnyomórészt digitálisan valósulnak meg, környező világunk jelei azonban analóg formában állnak rendelkezésre. A két oldal közötti átjárást biztosítják az analóg-digitális (A/D) átalakítók. Mivel számos sorozatgyártásba kerülő termék (pl. autóipari termékek, mobiltelefonok) tartalmaz A/D átalakítókat, az alkalmazott A/D-átalakítók száma is jelentős. Ennek következtében kritikus, hogy a teszteket numerikusan stabilan, és lehetőleg olcsón tudjuk végrehajtani. Kutatásom célja az A/D-átalakítók teszteléséhez szükséges szinuszillesztő algoritmusok numerikus kiértékelés szempontjából érzékeny pontjainak felderítése, valamint a tesztelés robusztus végrehajthatóságának biztosítása.

 

A kutatóhely rövid bemutatása

Kutatásaimat a Méréstechnika és Információs Rendszerek Tanszéken végzem a Digitális Jelfeldolgozás Laboratórium támogatásával. A Tanszéken egy A/D-átalakítókkal foglalkozó háromfős kutatócsoport munkájában veszek részt, mely Dr. Kollár István († 2016) irányítása alatt jött létre [L1].

 

A kutatás történetének, tágabb kontextusának bemutatása

A kutatás tágabb értelemben – ahogy a téma címe is mutatja – analóg-digitális átalakítók tesztelésével foglalkozik. Bár erre a feladatra rendelkezésre áll az IEEE 1241-es szabványa [8], felmerül a kérdés, hogy az elméletben könnyen teljesíthető kritériumok a gyakorlati megvalósítás során is teljesülnek-e. Az én feladatom a tesztelés numerikus, tehát számítógépes feldolgozáshoz köthető problémáinak felderítése és csökkentése. Más szavakkal kifejezve: melyek azok a pontok, amelyeken az algoritmusok hibái a számítási pontatlanságok miatt a vártnál jóval nagyobbak lehetnek, és mit lehet tenni ezen hibák csökkentésére.

Az analóg-digitális átalakítás során környezetünk analóg jeleit alakítjuk át a számítógép által feldolgozható digitális jellé. Ezt a folyamatot szemlélteti az 1. ábra. Az átalakítás során az időben és amplitúdóban folytonos jelet először mintavételezzük, majd kvantáljuk, vagyis időben és térben is diszkrétté tesszük.

 

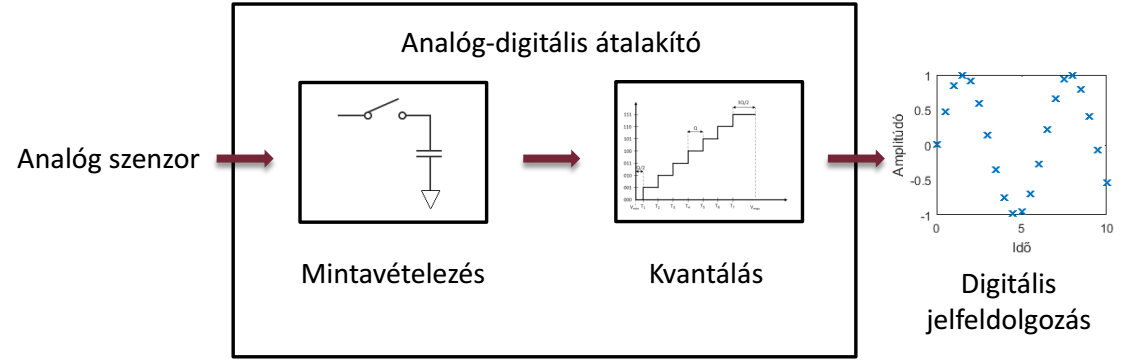
1.    ábra - Az analóg-digitális átalakítás folyamata

Az átalakítás jellemzőinek leírását, és mérésük módját az IEEE 1241-es szabványa definiálja [8]. Ezen belül az egyik legfontosabb módszer szinuszillesztés, mely során tisztán szinuszos gerjesztést alkalmazva megvizsgáljuk, hogy az átalakító kimenete mennyire követi egy ideális átalakító kimenetét.

 

A kutatás célja, a megválaszolandó kérdések

A szinuszillesztő algoritmusok futtatásához egy tisztán szinuszos bemeneti gerjesztést alkalmazva kell az A/D-átalakító kimeneti jelére szinuszt illeszteni. Egy egyenletesen, vagyis azonos időközönként mintavételezett szinuszos jelet általánosan a következőképpen írhatunk le:

 

 

ahol y_k a szinuszos jel k-dik eleme, A, B és C a jel koszinuszos, szinuszos és egyenkomponensének amplitúdói, f a jel frekvenciája, f_s pedig a mintavételi frekvencia. Az illesztett függvényben minden egyes időpontban ki kell számítani a szinusz- és koszinuszfüggvények fázisát:

Jól látható, hogy k növelésével a pillanatnyi fázis értéke is növekszik. A modern számítógépekben elterjedten használnak lebegőpontos számábrázolást (melyről részletesen a Módszerek pontban lesz szó). Szimpla pontosságú fáziskiértékelést alkalmazva az elkövetett kerekítési hiba relatív értéke 10^-7 nagyságrendű.

A pillanatnyi fázis, vagyis  kerekítési hibáit a 2. ábra mutatja (esetén) [2]. Megfigyelhető, hogy az elkövetett hiba maximális értéke lépcsőzetesen növekszik, továbbá minden intervallum szélessége és magassága is kétszerese az előzőnek. Vagyis minél több mintát veszünk, annál jelentősebb lesz az elkövetett hiba mértéke. Jól látható továbbá, hogy a szimpla pontosságú számábrázolás hibájánál (vagyis nagyságrendileg 10^-7) több nagyságrenddel nagyobb hiba is előfordul.

 

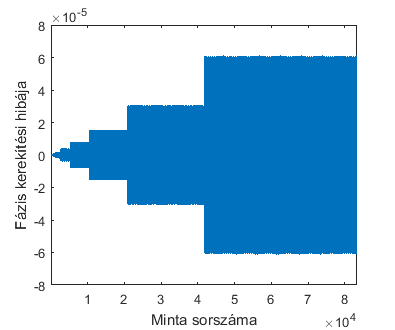
2.    ábra - Fáziskiértékelés hibája szimpla pontosságú számábrázolással

 

Dupla pontosságú számábrázolást alkalmazva természetesen a hiba mértéke jóval kisebb. Mégis érdemes a szimpla pontosságú kiértékeléssel foglalkozni, tekintve hogy ugyanazt a feladatot csekélyebb számítási képességgel rendelkező, ennek következtében olcsóbb eszközzel is szeretnénk megoldhatóvá tenni. A kutatás során megválaszolandó kérdés, hogy a fáziskiértékelés hibájából adódó pontatlanságok miként csökkenthetők, támogatva ezzel a szimpla pontosságú jelfeldolgozást.

 

Módszerek

Ahogy az előző pontban láttuk, a modern jelfeldolgozó egységek gyakran lebegőpontos számábrázolást alkalmaznak. Ez annak köszönhető, hogy segítségével széles dinamikatartományban közel állandó relatív hibával tudunk számokat ábrázolni. Lebegőpontos számábrázoláskor a számot normalizált alakban írjuk fel, hasonlóan a számológépekben ismert tudományos funkcióhoz. Például

vagyis van egy számunk (mantisszánk, jelen esetben 1,56343), melyet 10 megfelelő hatványra emelésével (exponens, jelen esetben -5) kell megszorozni, hogy az ábrázolni kívánt számot kapjuk. A módszer előnye, hogy nem kell sok 0-t eltárolni, és így az exponens segítségével széles dinamikatartományban tudunk számokat ábrázolni. Mivel a mantisszát csak véges hosszúságon tudjuk eltárolni (ez jelen esetben 6 hosszú), a tárolásnál kerekítési hiba lép fel. Ez a mantissza utolsó jegyét érinti, nagysága azonban függ az exponens nagyságától. Minél nagyobb az exponens, vagyis 10 minél nagyobb hatványával kell szorozni a mantisszát, annál nagyobb lesz a kerekítési hiba abszolút értéke. Azonban – és ez a módszer előnye – a maximális kerekítési hiba relatív értéke állandó marad az egész ábrázolható számtartományon. A számítógépekben szimpla pontosságú (single precision) számábrázolás esetén ez a relatív hiba 10^-7, míg dupla pontosságú számábrázolás esetén 10^-16 nagyságrendű - előbbi esetben 4, utóbbiban 8 bájton tárolható az ábrázolt lebegőpontos szám.

Ezekből világosan látszik, hogy az előző részben látott problémát az okozza, hogy a fázis abszolút értéke a minták számának növelésével szintén növekszik. Amennyiben ezt a növekedést korlátozni tudnánk, akkor a kerekítési hiba is korlátos maradna, hiszen a kerekítési hiba nagysága arányos az ábrázolt szám abszolút értékével.

A fázis abszolút értéke azonban egyszerűen korlátozható, hiszen ezt az információt szinusz és koszinuszfüggvények argumentumaként használjuk fel, melyek  szerint periodikusak. Tehát ha a tört fázisinformációt értékeljük ki a

 

 

képlet szerint, ahol  a törtrészképzés operátora, akkor annak kerekítési hibája jóval kisebb lesz, mint az eredeti esetben. A törtrészképzést most a legközelebbi egész számtól való eltérésként értelmezzük, tehát , és .

Fontos hangsúlyozni, hogy a törtrészképzést késő akkor elvégezni, amikor már kiszámoltuk fk/f_s-t. Ennek oka, hogy amennyiben a számítást elvégezzük, az eredményt el kell tárolnunk, mely esetben az eredeti nagy kerekítési hibák lépnek fel. Ezután hiába vonjuk le az egész részt, a pontos fázisinformációt már elvesztettük, ezért a tört rész sem lesz pontos. Ezért fontos, hogy az eredmény eltárolása előtt közbeavatkozzunk. Erre szolgál az inkrementális fáziskiértékelés [1]. Ebben a következő időpontbeli fázis törtrészét a

 

 

képlettel számíthatjuk, vagyis a következő időpontbeli számításhoz felhasználjuk a jelen pillanatbeli számítás eredményét – ebből adódik az inkrementális fáziskiértékelés elnevezés. A törtrészképzésnél meg kell vizsgálni, hogy a vizsgált szám nagyobb-e mint 0,5. Amennyiben igen, 1-et le kell vonni az eredményből, hogy megkapjuk a törtrészt. Ezzel biztosítjuk, hogy a kiszámított fázisinformáció a tartományba essen, ezáltal a fellépő kerekítési hibát is korlátozzuk.

Sajnos a problémát még így sem oldottuk meg teljesen, ugyanis lebegőpontos számábrázolás esetén az összegzés hibája sem 0. Szimpla pontosságú aritmetikát alkalmazva például

 

vagyis közel sem a várt 0 az eredmény. A probléma kiküszöbölésére a Kahan által javasolt kompenzált összegzést alkalmazhatjuk [10], mely minden egyes összegzési lépésnél kompenzál az előző lépésnél fellépett hibával. A kompenzált összegzéssel kiegészített inkrementális számítás már alkalmas arra, hogy a kerekítési hibákat jelentősen csökkentsük.

 

Eddigi eredmények

Ahhoz, hogy a fáziskiértékelési hiba csökkentésének jelentőségét szemléltessem, egy Monte Carlo analízist hajtottam végre, melyben 100 ezer különböző érték esetén vizsgáltam meg, hogy szimpla pontosságú kiértékelést alkalmazva mekkora a fáziskiértékelés hibájának maximuma az inkrementális fáziskiértékelést felhasználva. Minden szimulációs eset 10⁵ mintát tartalmazott. Az eredményeket a 3. ábrán ábrázoltam. Jól látható, hogy a hibák jóval kisebbek, mint a kompenzálás nélküli esetben - lásd 2. ábra. Ráadásul a hibák nagysága a szimpla pontosságú kiértékelés kerekítési hibáinak nagyságrendjébe esik.

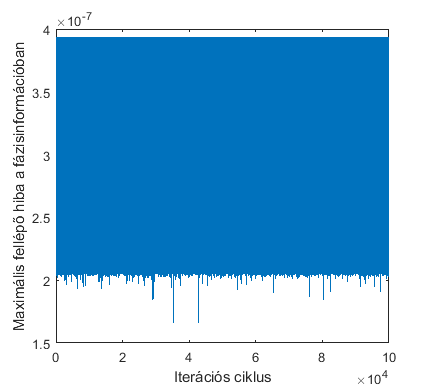
3.    ábra - Fáziskiértékelés maximális hibája a Monte Carlo analízisben, inkrementális fáziskiértékelést alkalmazva [1]

Bár a fáziskiértékelés hibáját csökkentettük, adódik a kérdés, hogy milyen hatása van ennek a gyakorlat - például analóg-digitális átalakítók tesztelése - során. Ehhez vizsgáljuk meg az effektív bitszám fogalmát. Az effektív bitszám (ENOB) azt adja meg, hogy az analóg-digitális átalakító névleges bitszámából mennyit használhatunk fel valójában. Ha egy névlegesen 16 bites átalakító ENOB értéke 14, az azt jelenti, hogy a különböző nemidealitások (felharmonikus torzítás, zajos átalakítás) következtében akkora hiba lesz a kimeneten, melynek hatására a legfinomabb felbontást adó két bit nem tud többletinformációt adni a bemeneti jelről.

A fáziskiértékelés kerekítési hibájának hatását a következőképpen szemléltethetjük: vegyünk egy ideális 12 bites A/D-átalakítót. Ezen átalakító effektív bitszáma is 12. Generáljunk 100 szinuszos gerjesztést, és vizsgáljuk meg, hogy mennyi a digitalizált jelből számított effektív bitszám dupla pontosságú és szimpla pontosságú számábrázolást alkalmazva. Továbbá értékeljük ki az átlagos ENOB értéket szimpla pontosságú számábrázolást alkalmazva, felhasználva a fáziskiértékelés hibájának csökkentésére javasolt algoritmust. Az eredményeket az 1. táblázat tartalmazza.

 

1.    táblázat - Átlagos effektív bitszám értékek különböző kiértékelések esetén

 

Jól látható, hogy 10 ezer minta esetén a különbségek elhanyagolhatók, azonban a minták számának növelésével a szimpla és a dupla pontosságú számítások különbsége egyre jobban növekszik. 100 ezer mintánál már több mint 1 bit a különbség az effektív bitszámban. Ez a hiba elsőrendűen a pontatlan fáziskiértékelésből adódik, hiszen szimpla pontosságú aritmetikát alkalmazva, a fáziskiértékelés pontosságának növelésével az effektív bitszám számításának hibája elhanyagolhatóvá válik.

A javasolt algoritmus felhasználásával tehát szimpla pontosságú aritmetikát alkalmazó eszközön is pontosan ki tudjuk értékelni az effektív bitszám értékét. Vagyis extra jelfeldolgozási lépések közbeiktatásával a feldolgozáshoz szükséges hardver költségét jelentősen csökkenteni tudjuk. Fontos továbbá hangsúlyozni, hogy az algoritmusban csak azokon a helyeken avatkozunk közbe, ahol a kerekítési hibák által okozott pontatlanság kritikus, így a kiszámítás ideje sem növekszik korlátlanul.

 

Várható impakt, további kutatás

Az analóg-digitális átalakítók tesztelése (többek között) szinuszillesztő algoritmus segítségével történik. Ennek megfelelően az IEEE 1241-es szabványa alapján minden egyes tesztelendő átalakító esetén futtatni kell egy szinuszillesztést, így fontos, hogy a teszteket a numerikus stabilitás mellett olcsón is tudjuk végrehajtani. A kutatás eredményei lehetővé teszik, hogy extra számítási lépések közbeiktatásával a szükséges hardverköltséget jelentősen csökkenteni lehessen.

A publikációk közül [1], [2] és [3] a neves IEEE Transactions on Instrumentation and Measurement folyóiratba került benyújtásra, mely az SJR (SCImago Journal & Country Rank) értékelése alapján a Q1 (vagyis felső 25%) besorolású mind „Electrical and Electronic Engineering”, mind „Instrumentation” tudományterületeken.

A kutatás a Dr. Kollár István vezetése alatt megkezdett „Optimális paraméterbecslési eljárások vizsgálata” OTKA-projekt (azonosító: K-115820) részét képezi. Kutatómunkám elismeréseként 2016-ban elnyertem a Pro Progressio Alapítvány Doktorandusz Ösztöndíját.

A numerikus javítási lehetőségek fejlesztésként terveink szerint be fognak kerülni a kutatócsoport által fejlesztett, ingyenesen elérhető MATLAB-toolboxba, melyet már több mint 10 országból töltöttek le [L1].

 

Saját publikációk

[1] B. Renczes, “Accurate Floating Point Argument Calculation for Sine Fitting Algorithms”, Kis módosítások esetén elfogadva az IEEE Transactions on Instrumentation and Measurement folyóiratban, 2017

[2]   B. Renczes, I. Kollár, A. Moschitta, P. Carbone, „Numerical Optimization Problems of Sine-Wave Fitting Algorithms in the Presence of Roundoff Errors”, IEEE Transactions on Instrumentation and Measurement, 65. kötet, 8. Szám, 1785-1795. oldal, 2016, doi: 10.1109/TIM.2016.2562218

[3]  B. Renczes, I. Kollár, “Efficient Implementation of Least Squares Sine Fitting Algorithms”, IEEE Transactions on Instrumentation and Measurement, 65. kötet, 12. szám, 2717-2724. oldal, doi: 10.1109/TIM.2016.2600998

[4]    B. Renczes, I. Kollár, P. Carbone, A. Moschitta, V. Pálfi, T. Virosztek, “Analyzing Numerical Optimization Problems of Finite Resolution Sine Wave Fitting Algorithms”, Proceedings of IEEE International Instrum. Meas. Technology Conference, 1662-1667. oldal, Pisa, Olaszország, 2015. május 11-14. doi: 10.1109/I2MTC.2015.7151529

[5]   B. Renczes, I. Kollár, ”Roundoff Errors in the Evaluation of the Cost Function in Sine Wave Based ADC Testing”, 20th IMEKO TC 4 Symposium and 18th IWADC Workshop, Benevento, Olaszország, 2014. szeptember 15-17.

        URL: http://www.imeko-tc4-2014.org/files/IMEKO_TC4_2014_proceedings.pdf.

[6]   B. Renczes, I. Kollár, ”Linearization of A/D converters using interpolation of samples”, 19th IMEKO TC 4 Symposium and 17th IWADC Workshop, Barcelona, Spanyolország, 2013. július 18-19.

        URL: http://mycite.omikk.bme.hu/doc/144252.pdf

[7]    B. Renczes, I. Kollár, “Compensation of Analog-to-Digital Converter Nonlinearities using Dither”, Periodica Polytechnica – Electrical Engineering 57 (3), 77-81. oldal (2013),

        doi: 10.3311/PPee.2145

 

Hivatkozások

[8]  Standard IEEE-1241-2010, “IEEE Standard for Terminology and Test Methods for Analog-to-Digital Converters” (2011) doi: 10.1109/IEEESTD.2011.5692956

 

[9]  IEEE Standard-754-2008, „IEEE Standard for Floating-Point Arithmetic”, 2008

       doi: 10.1109/IEEESTD.2008.4610935

[10] W. Kahan, “Further remarks on reducing truncation errors”, Communications of the ACM, 8. kötet, 1. szám, 40. Oldal, 1965, doi: 10.1145/363707.363723

 

Linkek

[L1] I. Kollár, T. Virosztek, V. Pálfi, B. Renczes, “ADCTest Project”

http://www.mit.bme.hu/projects/adctest