|
|
BMe Research Grant |
|
Doctoral School of Physics
Department of Atomic Physics
Supervisor: Dr. Gali Ádám
Study of quantum bits in diamond from first principles
Introducing the research area
Research and development in quantum technology is a hot topic in the EU and the entire world, which would lead to the development of new sensors for computation or communication and ultrasensitive detectors in the future. One possible realization of quantum bits is the paramagnetic and optically active point defects embedded in solids [1]. I have studied defect centres in diamond by means of computer simulations at the atomic scale.
Brief introduction of the research place
My research is being carried out as a member of the group of Prof. Adam Gali at the Department of Atomic Physics, and at the Wigner Research Centre for Physics, Hungarian Academy of Sciences. We use our small computing cluster and the Hungarian supercomputers operated by NIIF for large scale atomistic simulations that enable us to allocate hundreds of CPU cores with terabytes of memory.
History and context of the research
The most prominent and known example quantum bit in diamond is the nitrogen-vacancy (NV) defect centre [2]. The NV center exhibits a high spin ground state that can be spinpolarized by optical excitation up to 100% efficiency even at room temperature. The intensity from the photoexcitation highly depends on the spin state of the ground state. Thus the electronic spin can be both read out and initialized with the same process, and can be manipulated by microwave fields. The spin of individual NV centres can be manipulated individually with confocal microscope, thus the quantum bit can be realized. However, the properties of NV centre are not so ideal in every aspect, for example in quantum communication. Thus the identification of alternative quantum bits in diamond is essential, which can be used for various applications in quantum technology. The defects can be introduced into diamond intentionally or by accidental contamination. It is important to identify them as they may show optical or paramagnetic activity, which can greatly influence and govern the properties of quantum bits in diamond.
I have studied point defects which can spontaneously enter diamond during chemical vapor deposition (CVD) growth process. Oxygen and hydrogen are an example for such elements. During the heteroepitaxial growth silicon can diffuse into diamond from the substrate forming the silicon-vacancy (SiV) defect or quantum bit [3]. The germanium-vacancy (GeV) [4] and tin-vacancy (SnV) [5] defects were intentionally introduced into diamond by ion implantation (Figure 1).
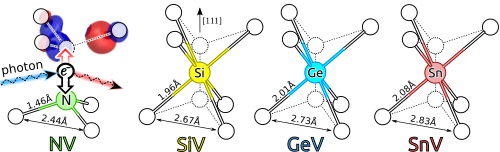
Figure 1. Geometry of the nitrogen-vacancy (NV), silicon-, germanium-, and tin-vacancy (SiV, GeV, and SnV) centres. The electronic spin of the NV centre can be initialized with illumination with visible light.
The research goals, open questions
The NV centre has been used as a quantum bit since more than a decade; however the exact mechanism behind the spinpolarization is yet to be understood. It is known from previous studies that the spin dependent fluorescence in NV centres is governed by the intersystem crossing processes between the singlet and triplet states. However, earlier theoretical models could not fully explain the experimental findings. Thus the development of a model for the intersystem crossings was one of our research goals.
I have also studied point defects other than the NV centre, which can be introduced spontaneously or intentionally in the diamond lattice. Oxygen can enter diamond spontaneously, but our knowledge is very limited about it, so my next goal was to explore the most important oxygen defects by means of atomistic simulations, and reveal their magneto-optical properties, with special emphasis on the possible quantum bit applications.
It is known that the negative SiV point defect behaves as a quantum bit. However, quantum operations can only executed at millikelvin temperatures due to the very weak small spin-orbit coupling. It is expected that the heavier elements of the group-IV exhibit much stronger spin-orbit interaction, which would allow increasing the operating temperature of quantum bits, which is a highly important aspect in quantum technology. Therefore, I aimed at determining the magneto-optical parameters of SiV, GeV, SnV, PbV centres, paying special attention to their possible applications in quantum technology.
Methods
I have treated the nuclei as classical ions (Born-Oppenheimer approximation), and I have determined the electronic structure by means of density functional theory (DFT) in my simulations at the atomic scale. I have typically embedded the defects in a diamond supercell containing 512 carbon atoms (Figure 1), that is sufficiently large to neglect the finite size effects from the limited size of the model. The aforementioned theoretical methods make it possible to determine the following physical properties of point defects:
● Position of nuclei at the equilibrium (1-3 figures).
● Magnetic dipole-dipole interactions between the spins of nuclei and electrons. (hyperfine structure)
●
Interaction of visible light and electronic structure: optically
excited states.
Photoluminescence
and
absorption of defects.
● Methods beyond the Born-Oppenheimer approximation: Jahn-Teller systems.
● Interaction between the angular moment and spin of electrons. (spin-orbit interaction)
I have determined the electronic structure with the VASP ab initio package, that even scales very well up to 1000 CPU cores. I was able to determine the physics of more than 1000 atoms simultaneously at quantum mechanics level within the foundations of DFT. I have developed my own code to determine the Jahn-Teller effect beyond the Born-Oppenheimer approximation with the numerical Gnu Octave environment. Furthermore, several improvements were also required in the VASP code, in order to determine the spin-orbit induced non-radiative transitions.

Figure 2. (a) The Bravais cell of diamond, which resembles the cubic symmetry of its lattice. (b) A diamond supercell containing a single NV centre with 510 carbon atoms. The opposing sides are connected during the quantum mechanical simulations, so the topology of the modeled system is a 3 dimensional torus.
Results
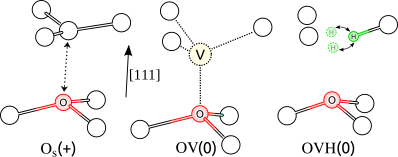
The examination of unknown point defects might largely contribute to the identification of quantum bit alternatives. Thus I have studied various unidentified complexes of hydrogen, oxygen and silicon with ab initio calculations [T10,T11]. One of such unidentified centre is the KUL12 electron paramagnetic resonance (EPR) centre in diamond, which I identified as the positively charged OS(+) defect (Figure 2).
Figure 3. Positively charged substitutional oxygen, neutral oxygen-vacancy defect, and the neutral oxygen-vacancy-hydrogen complex. All three defects are paramagnetic, and exhibit a 120° degrees threefold rotational symmetry. Due to quantum mechanical tunneling, the hydrogen of the OVH(0) centre seems to be simultaneously bound to all three carbons in electron paramagnetic resonance (EPR) measurements. In simple words, the hydrogen is continuously tunneling through the 3 bonds.
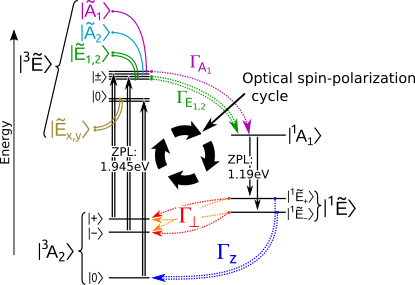
It is also an important task to examine the physics of point defects which have already been observed in experiments. Although the spinpolarization process of the negatively charged NV(-) is essential in the quantum technology applications, still the exact physical background is not yet completely understood (Figure 2). I have proven with my model that the nonradiative transitions are governed by (pseudo) Jahn-Teller effect and spin-orbit interactions simultaneously [T3,T7], which leads to the Sz=0 population at the end of the cycle under if the diamond sample is illuminated. Additionally, the NV centre has already been observed in multiple charge states, and this phenomenon was included in my modelling studies [T6].
Figure 4. The spinpolarization process of NV. The black arrows denote optical excitations (1.945 eV absorption and 1.19 eV luminescence). The colored arrows point to nonradiative (no photon emission) processes. If the 1.945 eV transition is activated with visible light, the |0〉substate with Sz=0 electronic spin of the |3A2〉ground state can be highly populated even at room temperature. Γ labels the rate of intersystem crossings. During my research, I have created a model and a microscopic theory to explain the physics of spinpolarization where I could calculate the intersystem crossing rates that agree well with the experimental data [T3,T7].
The requirement of theoretical calculations is clearly visible from the story of the OV(0) centre (Figure 3). The OV and NV point defects share a common 3A2 ground state (they are isoelectronic), and both defects exhibit an S=1 high spin in EPR experiments. It was initially proposed that the spin of OV can be polarized similarly to NV centre. However, the excited structure of OV is very different from that of the OV (Figure 5), thus the OV can exhibit neither any luminescent optical feature, nor optical spin polarization, in agreement with thw experimental findings [T10].
Figure 5. The nonradiative relaxation path of oxygen-vacancy. Whereas the NV can emit and absorb photons, the OV system can only absorb them. In the case of OV, one of the C-O bonds dissociates, thus a new nonradiative process emerges in OV, which is not observed in the NV centre.
I have examined the magneto-optical properties of SiV(-), GeV(-), SnV(-), PbV(-) defects [T1,T4,T5]. My results indicated that the spin-orbit interaction is greatly suppressed by the Ham[11] és Stevens[12] reduction factors, which I determined from first principles.
Expected impact and further research
One of the new hot topics in quantum technology is the identification and realization of solid state quantum bits, which can be used as ultrasensitive sensors [10,11,12], or can be used in the area of transmission of quantum information. Additionally, point defects can be useful as biological contrast agents in medical sciences [12]. In this research topic high precision atomistic simulations play an essential role, that can be used for the prediction of new quantum bits, or reveal the physical nature of those already known and use this knowledge for the optimization of their operation. My results would contribute to the realization of an optimal quantum bit in diamond, and provide a theoretical method to help revealing and examining new quantum bits in other solids.
Publications, references, links
List of corresponding own publications:
(IP, impact factor)
[T1] G. Thiering, A. Gali, Ab initio magneto-optical spectrum of group-IV-vacancy color centers in diamond. Phys. Rev. X 8, 021063 (2018) IP: 12.789
[T2] B. Rose, G. Thiering, … , A. Gali, S. Lyon, N. de Leon: Strongly anisotropic spin relaxation in the neutral silicon vacancy center in diamond e-print arXiv:, quant-ph/1702.01590.
[T3] G. Thiering, A. Gali: Theory on the optical spinpolarization loop of the nitrogen-vacancy center in diamond e-print arXiv: quant-ph/1803.02561.
[T4] E. Londero, G. Thiering, A. Gali, A. Alkauskas: e-print arXiv:, quant-ph/1605.02955. Vibrational modes of negatively charged silicon-vacancy centers in diamond from ab initio calculations.
[T5] Häußler S, Thiering G, Dietrich A, Waasem N, Teraji T, Isoya J, Iwasaki T, Hatano M, Jelezko F, Gali A, Kubanek A: Photoluminescence excitation spectroscopy of SiV(-) and GeV(-) color center in diamond New Journal of Physics 19:(6) Paper 063036. 9 p. (2017) IP: 3.786
[T6] Pfender M, Aslam N, Simon P, Antonov D, Thiering G, Burk S, Favaro de Oliveira F, Denisenko A, Fedder H, Meijer J, Garrido JA, Gali A, Teraji T, Isoya J, Doherty MW, Alkauskas A, Gallo A, Gruneis A, Neumann P, Wrachtrup J: Protecting a Diamond Quantum Memory by Charge State Control Nano Letters 17:(10) pp. 5931-5937. (2017) IP: 12.712
[T7] Thiering G, Gali A: Ab initio calculation of spin-orbit coupling for an NV center in diamond exhibiting dynamic Jahn-Teller effect Phys. Rev. B 96:(8) Paper 081115. 6 p. (2017) IP: 3.836
[T8] Udvarhelyi P, Thiering G, Londero E, Gali A: Ab initio theory of the N2V defect in diamond for quantum memory implementation Phys. Rev. B 96:(15) Paper 155211. 7 p. (2017) IP: 3.836
[T9] Gali A, Demján T, Vörös M, Thiering G, Cannuccia E, Marini A: Electron-vibration coupling induced renormalization in the photoemission spectrum of diamondoids Nat. Comm. 7: Paper 11327. 9 p. (2016) IP: 12.124
[T10] Thiering G, Gali: A Characterization of oxygen defects in diamond by means of density functional theory calculations Phys. Rev. B 94:(12) Paper 125202. 15 p. (2016) IP: 3.836
[T11] Thiering G , Gali A: Complexes of silicon, vacancy, and hydrogen in diamond: A density functional study Phys. Rev. B 92:(16) Paper 165203. 15 p. (2015) IP: 3.718
[T12] Thiering G, Londero E, Gali: A Single nickel-related defects in molecular-sized nanodiamonds for multicolor bioimaging: an ab-initio study Nanoscale 6: pp. 12018-12025. (2014) IP: 7.394
Table of links:
Webpages of the research group and Dr. Ádám Gali:
http://www.fat.bme.hu/kulonc/galia/
Wikipédia pages:
https://en.wikipedia.org/wiki/Qubit
https://en.wikipedia.org/wiki/Jahn–Teller_effect
https://en.wikipedia.org/wiki/Quantum_chemistry
Other:
https://wiki.kfki.hu/nano/Defects_for_quantum_information_processing
https://wiki.kfki.hu/nano/Defect_Identification
List of references:
[1] J. R. Weber, W. F. Koehl, J. B. Varley, A. Janotti, B. B. Buckley, C. G. Van de Walle, and D. D. Awschalom: Quantum computing with defects - Proceedings of the National Academy of Sciences 107 19, 8513–8518 (2010)
[2] Doherty, M. W., Manson, N. B., Delaney, P., Jelezko, F., Wrachtrup, J., & Hollenberg, L. C. (2013). The nitrogen-vacancy colour centre in diamond. Physics Reports, 528(1), 1-45.
[3] Sukachev, D. D., Sipahigil, A., Nguyen, C. T., Bhaskar, M. K., Evans, R. E., Jelezko, F., & Lukin, M. D. (2017). Silicon-Vacancy Spin Qubit in Diamond: A Quantum Memory Exceeding 10 ms with Single-Shot State Readout. Physical review letters, 119(22), 223602.
[4] Bhaskar, M. K., Sukachev, D. D., Sipahigil, A., Evans, R. E., Burek, M. J., Nguyen, C. T., ... & Jelezko, F. (2017). Quantum nonlinear optics with a germanium-vacancy color center in a nanoscale diamond waveguide. Physical review letters, 118(22), 223603.
[5] Tchernij, S. D., Herzig, T., Forneris, J., Küpper, J., Pezzagna, S., Traina, P., ... & Genovese, M. (2017). Single-photon-emitting optical centers in diamond fabricated upon Sn implantation. ACS Photonics, 4(10), 2580-2586.
[6] Goldman, M. L., Sipahigil, A., Doherty, M. W., Yao, N. Y., Bennett, S. D., Markham, M., ... & Lukin, M. D. (2015). Phonon-induced population dynamics and intersystem crossing in nitrogen-vacancy centers. Physical review letters, 114(14), 145502.
[7] Bersuker, I. (2013). The Jahn-Teller effect and vibronic interactions in modern chemistry. Springer Science & Business Media.
[8] Ham, F. S. (1965). Dynamical Jahn-Teller effect in paramagnetic resonance spectra: orbital reduction factors and partial quenching of spin-orbit interaction. Physical Review, 138(6A), A1727.
[9] Stevens, K. W. H., & Pryce, M. H. L. (1953). On the magnetic properties of covalent XY 6 complexes. Proc. R. Soc. Lond. A, 219(1139), 542-555.
[10] Maletinsky, P., Hong, S., Grinolds, M. S., Hausmann, B., Lukin, M. D., Walsworth, R. L., ... & Yacoby, A. (2012). A robust scanning diamond sensor for nanoscale imaging with single nitrogen-vacancy centres. Nature nanotechnology, 7(5), 320.
[11] Dolde, F., Fedder, H., Doherty, M. W., Nöbauer, T., Rempp, F., Balasubramanian, G., ... & Wrachtrup, J. (2011). Electric-field sensing using single diamond spins. Nature Physics, 7(6), 459.
[12] Kucsko, G., Maurer, P. C., Yao, N. Y., Kubo, M. I. C. H. A. E. L., Noh, H. J., Lo, P. K., ... & Lukin, M. D. (2013). Nanometre-scale thermometry in a living cell. Nature, 500(7460), 54.