Fizikai Tudományok Doktori Iskola 

TTK, Atomfizika Tanszék

Témavezető: Dr. Gali Ádám

Szilárdtestbeli kvantumbitek elméleti vizsgálata

A kutatási téma néhány soros bemutatása

 Napjainkban a kvantumtechnológia forradalmát éljük. A kvantumszámítógépek alkalmazásával bizonyos műveletekhez szükséges idő nagyságrendekkel lecsökkenthető, valamint a kvantumkommunikáció bevezetésével a kvantuminformáció titkosítása tökéletesíthető. A kvantuminformatika fontos építőelemei a kvantumbitek (vagy qubitek), amelyek - a klasszikus bit mintájára - a kvantuminformáció tárolását, illetve hordozását végző műveleti egységek. A qubitek fizikai reprezentációi kétállapotú kvantumrendszerek, amelyeknek több konkrét megvalósítása létezik. Ilyenek lehetnek szilárdtestekbe beépülő paramágneses ponthibák [1], amelyek elektronspin-állapotába kódolható az információ. Fontos szempont, hogy a kristályos anyag széles tiltott sávú félvezető legyen, valamint az, hogy a ponthiba mélyen a tiltott sávon belül létrehozzon elektronállapotokat egy zérusnál nagyobb eredő spinű elektronszerkezetet kialakítva. Ezeknek a feltételeknek megfelelnek szilícium-karbidba (SiC) beépülő bizonyos ponthibák, amelyek – kísérleti és elméleti eredmények alapján – nagyon ígéretesnek bizonyultak kvantumtechnológiai alkalmazások tekintetében. A kutatásom során ilyen rendszerek elméleti vizsgálatát végzem el modern elektronszerkezet-számítási technikák segítségével.

 

A kutatóhely rövid bemutatása

Kutatásomat a Félvezető Nanoszerkezetek Lendület Kutatócsoport (vezető kutató: Dr. Gali Ádám) gondozásában a BME Atomfizika Tanszéken, valamint az MTA Wigner Fizikai Kutatóközpontban végzem. A nagy számításigényű elektronszerkezet-számításokat a kutatócsoport, valamint a Nemzeti Információs Infrastruktúra Fejlesztési Intézet szuperszámítógépein valósítom meg a Vienna Ab Initio Simulation Package (VASP) [2] programcsomag segítségével.

 

A kutatás történetének, tágabb kontextusának bemutatása

A munkám célja olyan SiC-beli ponthibák vizsgálata, amelyek potenciálisan alkalmasak lehetnek kvantumtechnológiai alkalmazásokra. Ilyen ponthiba lehet egyetlen beépült hiba atom a SiC egyik rácshelyén egy Si vagy C atomot helyettesítve (szubsztitúciós ponthiba), egy üres rácshely (Si- vagy C-vakancia), de akár egymás mellett lévő több hiba atom és/vagy vakancia (hibakomplexum) is alkothat qubitot. Az ilyen rendszerek leghíresebb képviselője az ún. nitrogén-vakancia hiba gyémántban [3], amely egy C atomot helyettesítő szubsztitúciós N és egy szomszédos Si vakanciából áll. Speciálisan a kvantumbit állapotot az egyszeresen negatív töltésű NV hiba valósítja meg S = 1 spinállapottal, emiatt elnevezték NV-centrumnak. Ezen a rendszeren elvégezhető az optikai spinpolarizáció folyamata, azaz bizonyos hullámhosszú lézerfény segítségével manipulálható a spinállapot akár szobahőmérsékleten is. Ebből kifolyólag az információ optikai úton írható és ki is olvasható az NV-centrum spinállapotából. A nagy sikere ellenére a gyémántbeli NV-centrum mutat hátrányokat is, például az optikai kiolvasás hullámhossza kívül esik a - kvantumkommunikáció szempontjából ideális - közeli infravörös (NIR) tartományon, valamint a gyémánt nehezen integrálható a félvezető elektronikai eszközökbe. A gyémánttal szemben a SiC-nak kiforrott félvezetőipari technológiája van, és ideális anyagnak bizonyult hasonlóan ígéretes, NIR emissziót mutató ponthibák beágyazásához.

 

A kutatás célja, a megválaszolandó kérdések.

 A SiC egy politípusos anyag, azaz különböző rácsszerkezetekben kristályosodhat. A technológiailag fontosabb politípusai a 3C, 4H és 6H SiC (1. ábra). Fontos megjegyezni, hogy a SiC egyes politípusaiban eltérő szimmetriájú rácshelyek találhatóak a lokális kristálykörnyezettől függően: egy rácshely lehet hexagonális (h) vagy köbös (k) lokális szimmetriájú. Ennek köszönhetően ugyanaz a ponthiba több különböző hibakonfigurációt hozhat létre (2. ábra).

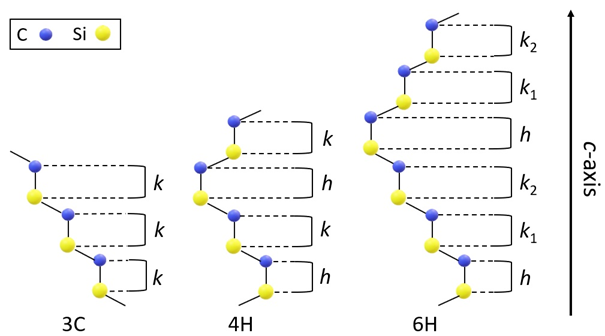
1.     ábra: Fontosabb SiC politípusok elemi cellája. A politípusok Si- kettős atomi rétegekből épülnek fel, amelyeket alkotó rácshelyek lokális szimmetriája lehet köbös (k) vagy hexagonális (h) az ábra alapján. Több k/h réteg esetén számozással különböztetjük meg az ugyanolyan szimmetriájú rétegeket. A kristálytengely (c-tengely) merőleges a kettősrétegekre.

 

Kézenfekvő megvizsgálni a SiC-beli NV-centrumot, amely várhatóan - a gyémántbeli megfelelőjéhez hasonlóan - egyedülálló tulajdonságokkal rendelkezik. A kutatásom során megvizsgáltam az NV-centrum mágneses és optikai tulajdonságait, valamint képződésének és alkalmazhatóságának feltételeit. A SiC-ban létrejövő divakancia – ami egy Si- és egy szomszédos C-vakanciából álló hibakomplexum (2. ábra) – NIR emissziót mutat [4] csak úgy, mint az NV-centrum. Továbbá sikerült rajta demonstrálni az optikai spinpolarizáció folyamatát [5] jelezve, hogy a SiC-beli divakancia is egy nagyon ígéretes qubit-jelölt. Ugyanakkor megfigyelték, hogy a divakanciához köthető fotonemisszió (fotolumineszcencia) egy, a vártnál nagyobb gerjesztési energia felett jelenik meg, ez alatt elnyomódik [S3, S4]. A felállított fizikai modell [S4] szerint a divakancia a vizsgált SiC-mintákban negatív töltésállapotba kerül az említett küszöbenergia alatti gerjesztés esetén, ugyanakkor a kvantumbit állapotot a semleges töltésállapot valósítja meg. A felállított fizikai modellt sikerült számításaimmal alátámasztani, továbbá protokollt kidolgozni a divakancia semleges töltésállapotának megtartására és szimultán optikai gerjesztésére, ami a qubit manipulációhoz elengedhetetlen.

 

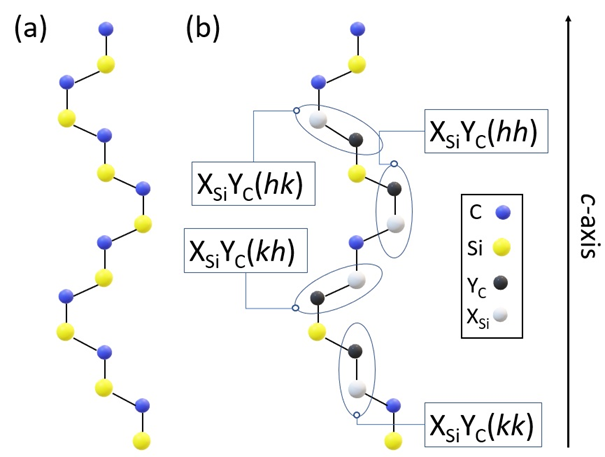
2.     ábra: (a) Tökéletes 4H SiC és (b) két szomszédos hiba atomból (X_Si, Y_C) vagy vakanciá(k)ból álló hibakomplexumot tartalmazó 4H SiC, ahol ábrázoltam az összes lehetséges hibakonfigurációt. X_Si = V_Si és Y_C = N_C esetén az nitrogén-vakancia hibát, míg X_Si = V_Si és Y_C = V_C megfeleltetéssel a divakancia hibaszerkezetét kapjuk meg. A ponthibák jelölésében zárójelben jelöltem rendre az első és a második hibaatom helyének lokális szimmetriáját.

 

Módszerek

Az atomi szintű elektronszerkezet számításhoz az első elvű sűrűségfunkcionál elméletet (DFT) alkalmaztam, az ún. Born-Oppenheimer (BO) -közelítés felhasználásával. A BO-közelítés a kristályban lévő atommagok mozgását jóval nagyobb tömegük miatt az elektronok mozgásától függetlenül kezeli, azaz lehetőséget ad az elektronszerkezet meghatározására tetszőleges stacionárius atomi pozíciók mellett. Ilyen módon a rendszer minimális energiája abban az atommag-konfigurációban lesz, ahol a legalacsonyabb a hozzá tartozó elektronrendszer teljes energiája. Ezt a konfigurációt relaxált geometriának nevezzük. Fontos megjegyezni, hogy azokban az esetekben, amikor erős az elektronok és magok mozgásának, azaz a rácsrezgések (fononok) kölcsönhatása (elektron-fonon csatolás) a BO-közelítés nem ad kielégítő eredményeket, és emiatt további módszerekre lehet szükség. A DFT egy független-részecske közelítést alkalmazó módszer, ami azt jelenti, hogy minden elektronra külön-külön meg tudjuk határozni a hozzátartozó energiaszintet. Fontos, hogy ebben a közelítésben nem valódi, hanem nem-kölcsönható kvázi-elektronokat tekintünk, így az egyelektron energiáknak nincs explicit fizikai jelentésük.

Az ponthibákat tömbi SiC-ban vizsgáltam, amely modellezéséhez ideális az ún. szupercella módszer használata. Ebben a modellben egy olyan cellát építünk, amely a SiC-egységcella egész számú többszöröse mindhárom irányban, és az így készült szupercella közepére elhelyezzük a ponthibát (3. ábra). A számítások során periodikus határfeltételt alkalmazva a szupercellákkal „kicsempézzük” a teret. Emiatt akkora szupercellát kell választanunk, ami már elég nagy ahhoz, hogy a ponthiba kölcsönhatása saját képeivel elhanyagolható legyen. Az elektromosan töltött ponthibák esetén megjelenő hosszútávú Coulomb-kölcsönhatásnak köszönhetően elméletben végtelen nagy szupercellát kellene alkalmaznunk, ami egyértelműen kivitelezhetetlen. Az ebből eredő mesterséges energiajárulékokat ún. töltéskorrekciók [6] segítségével tudjuk orvosolni. Az általam vizsgált ponthibák esetén elfogadhatóan pontos eredményeket kaptam ~500 atomos szupercellákat alkalmazva.

 

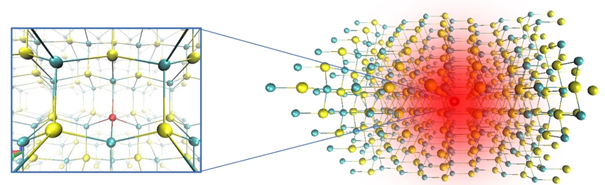
3. ábra: A SiC szupercellája és a benne középen elhelyezett - ebben az esetben - egyetlen hiba atomból álló szubsztitúciós ponthiba. A piros folt a ponthiba NIR emisszióját jelzi, amely tulajdonság fontos kvantumtechnológiai alkalmazások szempontjából.

 

A használt módszerek segítségével kiszámítható az alap és első gerjesztett állapotok közti optikai átmenetek energiája, amit zérus-fonon vonalnak (ZPL) hívnak tekintve, hogy ekkor nem tekintjük a fononokkal csatolt elektronátmeneteket. Kiszámítható továbbá a ponthiba képződési energiája, valamint az ún. betöltési szintek, amely a Fermi-szintnek azon pozíciói, ahol a két töltésállapot képződési energiája megegyezik. Az elektronszerkezetben felmerülő mágneses felhasadások is meghatározhatók: az elektronok és atommagok spinjének kölcsönhatásából adódó hiperfinom felhasadás, az elektron spin – elektron spin kölcsönhatásból származó nulltér-felhasadás (ZFS), valamint megbecsülhető az elektron spin- és pályamomentum kölcsönhatásából adódó spin-pálya felhasadás is. A magnetooptikai tulajdonságok nem csupán a ponthiba kvantumtechnológiai alkalmazhatóságára adnak választ, de egyediségüknek köszönhetően rajtuk keresztül azonosítható a ponthiba egy adott mintában a kísérleti és számítási értékük, illetve az értékekben fellelhető trendek összehasonlításával.

 

Eddigi eredmények

Nitrogénnel adalékolt 4H SiC mintákon végzett fotolumineszcencia (PL) mérésekben megfigyeltek 4 - eddig nem azonosított - ZPL-et a NIR tartományban [S5, S8]. Elektron-paramágneses rezonancia (EPR) mérésekből nyert adatok is rendelkezésre állnak ugyanarra a ponthibára, amely a forrása lehet az ismeretlen ZPL-eknek [S5, S8]. A kiszámított ZPL-ek, hiperfinom és nulltérfelhasadást jellemző állandók alapján beláttam, hogy az ismeretlen ponthiba az NV-centrum, amely 4 különböző hibakonfigurációt hozhat létre a 4H SiC rácsstruktúrájának köszönhetően (2. ábra). Kiszámítottam továbbá az NV-centrum hibakonfigurációk és más szokásosan kialakuló ponthibák képződési energiáit a 4H politípusban, amelyekből megbecsültem a termodinamikai egyensúlyban [pl. kémiai gőzfázisú leválasztás során (CVD)] keletkező ponthibák koncentráció viszonyait (4. ábra). Eredményeim alapján a figyelembe vett ponthibák közül egy nemzérus spinű ponthiba keletkezhet kb. 7 nagyságrenddel nagyobb koncentrációban, a C rácshelyű szubsztitúciós nitrogén. Az így létrejövő nagy spinkoncentráció ellehetetlenítheti az NV-centrum felhasználását. Ponthibák létrehozására egy másik szokásos eljárás az ionimplantáció. Ennek során N ponthibák és vakanciák keletkeznek nagy mennyiségben. Az ezt követő hőkezelés során ezek a ponthibák mozgékonnyá válnak és összekapcsolódhatnak NV-centrumokat és divakancia ponthibákat alkotva. Az eredményeim alapján az NV-centrum mellett semleges töltésállapotú (S=1 spinű) divakancia megjelenése mindig várható a 3C, 4H és 6H politípusokban (ezt a kísérleti megfigyelések is megerősítik). Ráadásul a divakancia optikailag aktív az NV-centrum gerjesztési tartományában, ami erősen ronthatja az NV-centrum fotostabilitását. A fentiek alapján a SiC-beli NV-centrum előállításához a szokásostól eltérő minta-előkészítési technikákra van szükség, mindazonáltal megjegyzendő, hogy kellően magas N koncentráció mellett az NV-centrum aránya várhatóan növelhető implantációs eljárással készült mintákban [S5-S8].

 

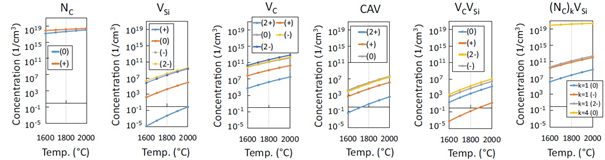
4. ábra: A vizsgált ponthibák koncentrációja CVD eljárással preparált 4H SiC minta esetében a szokásos hőmérsékleteken. A ponthibák balról jobbra: szubsztitúciós N hiba, Si vakancia, C vakancia szén antihely - vakancia pár, divakancia és különböző mennyiségű N atommal körülvett Si vakancia [S5].

 

                    A divakancia az NV-centrumhoz hasonlóan szintén 4 különböző hibakonfigurációt hozhat lére a 4H SiC rácsában (2. ábra). Kutatásom során a divakanciához köthető – már említett – PL elnyomódást vizsgáltam. A mikroszkopikus modell szerint a gerjesztési küszöbenergiát elérve a jelenlévő negatív töltésállapot újraionizálódik, megjelenik a semleges divakancia és ezzel a hozzá köthető ZPL-ak is. A negatív töltésállapot újraionizációja egy elektron gerjesztésével történhet meg a legmagasabb betöltött tiltott sáv állapotról a vezetési sávba (CB). Az ehhez szükséges energiát megbecsültem a 0/- betöltési szint CB minimumtól való távolság kiszámításával. A négy különböző divakancia-konfigurációra kapott számítási eredményeket összevetve a gerjesztési küszöbenergiákkal jó egyezést kaptam, ami alátámasztja a részletezett fizikai modellt. A divakancia semleges töltésállapotának kontrolja és szimultán gerjesztése egyetlen lézerrel fontos szempont. Mivel a gerjesztési energia alacsonyabb a küszöbenergiáknál, a kulcs a hőmérséklet emelése lehet, amelynek segítségével fononok kelthetők. Az alacsonyabb – általánosan alkalmazott – gerjesztési (~1.27 eV) energia összeadva a fononenergiával elegendő lehet a divakancia újraionizációjára is. Számítási eredményeim arra utalnak, hogy kb. szobahőmérsékleten (kb. 300 K-en) már jelentős valószínűséggel megtörténhet az újraionizáció (5. ábra), csak úgy, mint a semleges állapot gerjesztése, azaz a qubitmanipuláció [S3, S4].

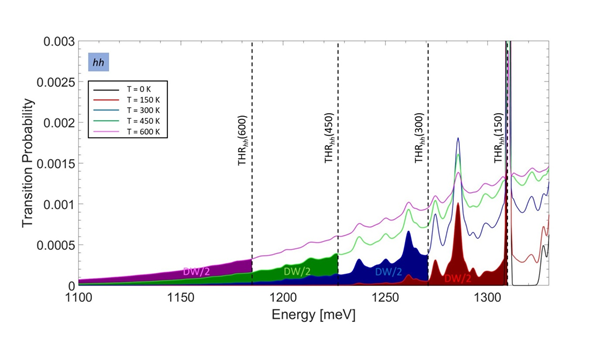
5. ábra: A divakancia hh konfiguráció magasabb hőmérsékleteken kiszámított (1-re normált) PL-spektruma, azaz az újraionizációt okozó elektronátmenet valószínűsége a gerjesztési energia függvényében. A színezett terület mutatja az adott küszöbenergia (THR) esetén bekövetkező kumulatív átmeneti valószínűséget, amit ebben az esetben az ún. Debye-Waller (DW) -faktor felének választottam. A DW-faktor a ZPL által bezárt terület nagysága, emiatt zérus hőmérsékleten a ZPL pozíciójában történő gerjesztés átmeneti valószínűsége épp DW/2. Látható, hogy 300 K-en, az alkalmazott gerjesztési energia mellett már jelentős valószínűséggel újraionizálódhat a divakancia.

 

Várható impakt, további kutatás

A kapott eredmények várhatóan jelentősen hozzájárulnak majd a vizsgált ponthibák kvantumbitként történő alkalmazásához. Ezenfelül az ilyen rendszerek hasznosíthatók lehetnek biológiai jelzőrendszerként az orvoslásban [7], valamint ultraérzékeny nanoszenzorok építőelemeiként [8]. További kutatási cél a SiC-ba beépülő átmeneti fém (TM) ponthibák vizsgálata, ezen belül is a vanádium és molibdén ponthibák, amelyek – korábbi kísérleti és elméleti eredmények [S2, 9] alapján - szintén ideális jelöltek lehetnek a kvantumkommunikációban egyfotonforrásként vagy kvantummemóriaként történő alkalmazásokhoz. A TM-atomok erősen korrelált d-pályáiknak köszönhetően érdekes fizikát mutatnak, amelyek megértése kulcsfontosságú az említett alkalmazásokhoz. Ebben és további kvantumbitek felfedezésében és természetének megértésben az atomi szintű szimulációk a jövőben is komoly szerepet játszhatnak, hiszen már eddig is úttörő eredmények sorát mutatták be ezen módszerek alkalmazásával.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

 

[S1]     A. Csóré, A. Gali, „Ab initio study on highly anisotropic magnetic properties of Kramers doublet systems”, előkészületben

 

[S2]     L. Spindelberger, A. Csóré, G. Thiering, S. Putz, N. T. Son, R. Karhu, J. Ul Hassan, T. Fromherz, A. Gali and M. Trupke, Optical Properties of Vanadium in 4H Silicon Carbide for Quantum Technology, elfogadva a Phys. Rev. Appl. (IF: 4.782) folyóiratnál, arXiv: 1901.05371 (2019)

 

[S3]     A. Csóré, B. Magnusson, N. T. Son, A. Gällström, T. Ohshima, I. G. Ivanov, A. Gali, First-principles study on photoluminescence quenching of divacancy in 4H SiC, Materials Science Forum, elfogadva

 

[S4]     B. Magnusson, N. T. Son, A. Csóré, A. Gällström, T. Ohshima, A. Gali and I. G. Ivanov, Excitation properties of the divacancy in 4H-SiC, Phys. Rev. B 98, 195202 (2018), IF: 3.813

 

[S5]     A. Csóré, H. J. von Bardeleben, J. L. Cantin, A. Gali, Characterization and formation of NV centers in 3C, 4H and 6H SiC: an ab initio study, Phys. Rev. B 96, 085204 (2017), IF: 3.813

 

[S6]     A. Csóré, Electronic structure and magneto-optical properties of NV centers in 4H and 6H SiC, Proceedings of the PhD workshop of the Physics Doctoral School at the Faculty of Science, pp. 21–24. (2017), IF: -

 

[S7]     A. Csóré and Á. Gali, Density functional theory on NV center in 4H SiC, Mat. Sci. For., Vol. 897, pp. 269–274 (2016), IF: -

 

[S8]     H. J. von Bardeleben, J. L. Cantin, A. Csóré, A. Gali, E. Rauls, U. Gerstmann, NV centers in 3C, 4H, and 6H silicon carbide: A variable platform for solid-state qubits and nanosensors, Physical Review B 94, p. 121202 (2016), IF: 3.813

 

Linkgyűjtemény.

 

Kvantumbit

Félvezető Nanoszerkezetek Lendület Kutatócsoport

BME Atomfizika Tanszék

MTA Wigner Fizikai Kutatóközpontban

VASP

NV-centrum

Sűrűségfunkcionál elmélet (DFT)

Born-Oppenheimer (BO) -közelítés

 

 

Hivatkozások listája.

 

[1]         J. R. Weber, W. F. Koehl, J. B. Varley, A. Janotti, B. B. Buckley, C. G. Van de Walle and D. D. Awschalom, Quantum computing with defects, Proc. Natl. Acad. Sci. USA 107, 8513 (2010)

 

[2]        G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996)

 

[3]        M. W. Doherty, N. B. Manson, P. Delaney, F. Jelezko, J. Wrachtrup and L. C. Hollenberg, The nitrogen-vacancy colour centre in diamond, Phys. Rep. 528, 1 (2013)

 

[4]        W. F. Koehl, B. B. Buckley, F. J. Heremans, G. Calusine and D. D. Awschalom, Room temperature coherent control of defect spin qubits in silicon carbide, Nature (London) 479, 84 (2011)

 

[5]        D. J. Christle, P. V. Klimov, C. F. de las Casas, K. Szász, V. Ivády, V. Jokubavicius, J. U. Hassan, M. Syvӓjӓrvi, W. F. Koehl, T. Ohshima, N. T. Son, E. Janzén, A. Gali and D. D. Awschalom, Isolated spin qubits in SiC with a high-fidelity infrared spin-to-photon interface, Phys. Rev. X 7, 021046 (2017)

 

[6]        H-P. Komsa, T. T. Rantala and A. Pasquarello, Finite-size supercell correction schemes for charged defect calculations, Phys. Rev. B 86, 045112 (2012)

 

[7]        G. Kucsko, P. C. Maurer, N. Y. Yao, M. Kubo, H. J. Noh, P. K. Lo, H. Park and M. D. Lukin, Nanometer scale thermometry in a living cell, Nature 500(7460), 54 (2013)

 

[8]        P. Maletinsky, S. Hong, M. S. Grinolds, B. Hausmann, M. D. Lukin, R. L. Walsworth, M. Loncar and A. Yacoby, A robust scanning diamond sensor for nanoscale imaging with single nitrogen-vacancy centres, Nature Nanotechnology 7(5), 320 (2012)

 

[9]        T. Bosma, G. J. J. Lof, C. M. Gilardoni, O. V. Zwier, F. Hendriks, B. Magnusson, A. Ellison, A. Gӓllström, I. G. Ivanov, N. T. Son, R. W. A. Havenith and C. H. van der Wal, Identification and tunable optical coherent control of transition-metal spins in silicon carbide, npj Quantum Information 4, 48 (2018)