|
|
BMe Research Grant |
|
Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering
Department of Applied Mechanics, Faculty of Mechanical Engineering
Supervisor: Dr. Csernák Gábor
Experimental and theoretical investigation of micro-chaos
Introducing the research area
The main focus of the research area is the deep understanding of micro-chaos (small amplitude chaotic oscillations). Micro-chaotic behaviour typically occurs in digitally controlled systems due to the so-called digital effects (sampling, round-off, delay).
Brief introduction of the research place
The research takes place at the Department of Applied Mechanics. The department conducts internationally recognized, high-standard research in several areas of applied mechanics. This is illustrated by the outstanding results of the SIREN ERC project, the Lendület human balancing research group and the MTA-BME Research Group on Dynamics of Machines and Vehicles.
History and context of the research
Nowadays, digitally (or computer) controlled devices are widespread (from assembly line robots to 3D printers), but designing and operating them introduces new challenges. Digital control typically occurs periodically, at specific sampling times. At these moments, the computer examines the current state and calculates the necessary amount of intervention, then drives the control components. Usually time delay is also present, since some amount of computation time is needed between the measurement of the state and the control. Since digital signals are represented by finite number of bits, round-off occurs during analog to digital conversions.
These digital effects (sampling, time delay and round-off) can cause small amplitude chaotic oscillations; the so-called micro-chaos.
The discovery of the phenomenon of micro-chaos is corresponding to Dr. Gábor Stépán, Dr. György Haller and Dr. Enikov Eniko [1, 2] during the second half of the 90’s. In the past two decades, Dr. Gábor Csernák has actively contributed to the corresponding research areas.
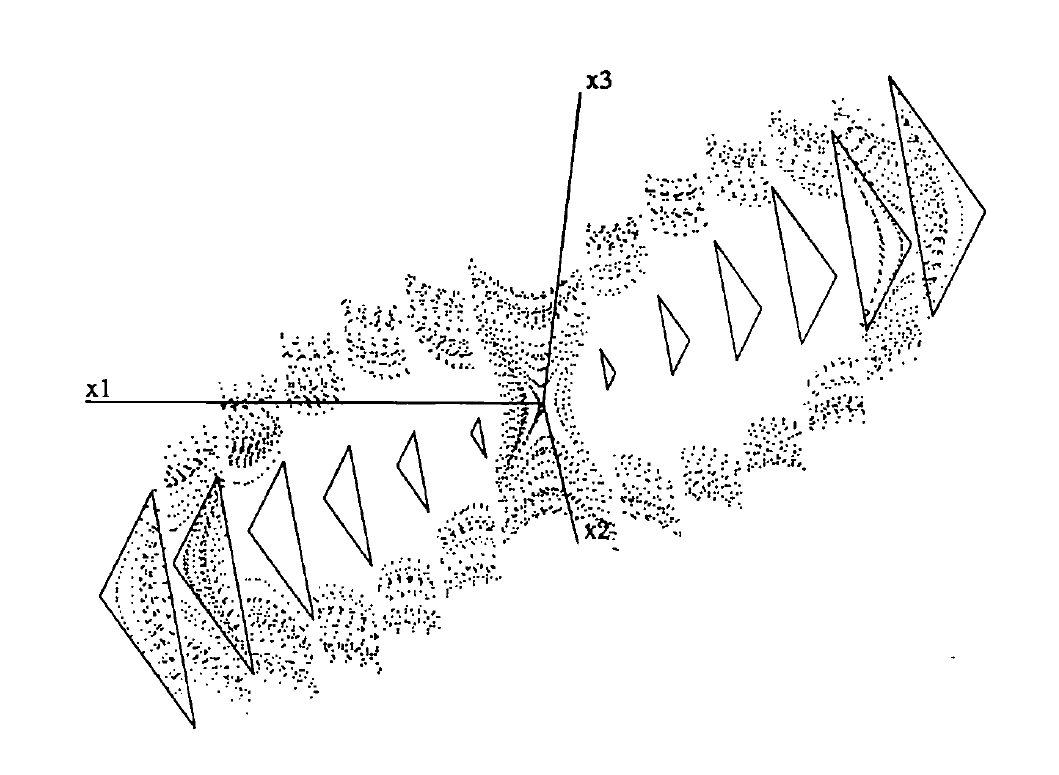
Figure 1.: Strange attractor in the phase space of a micro-chaos map [1].
Due to its small amplitude, micro-chaos is usually neglected in practice, or considered as random noise. This step, although makes impossible to examine the underlying patterns of micro-chaotic behaviour or the possibility to exploit its presence in some cases.
The research goals, open questions
One of the simplest systems which exhibit micro-chaotic behaviour is the digitally controlled inverted pendulum (see Fig. 2).
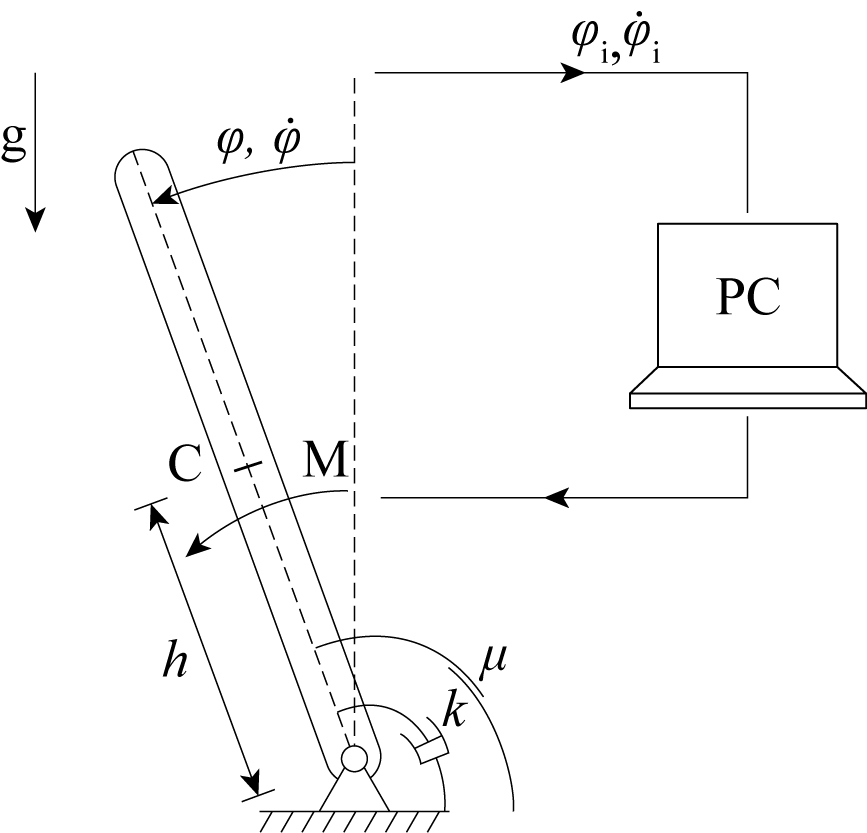
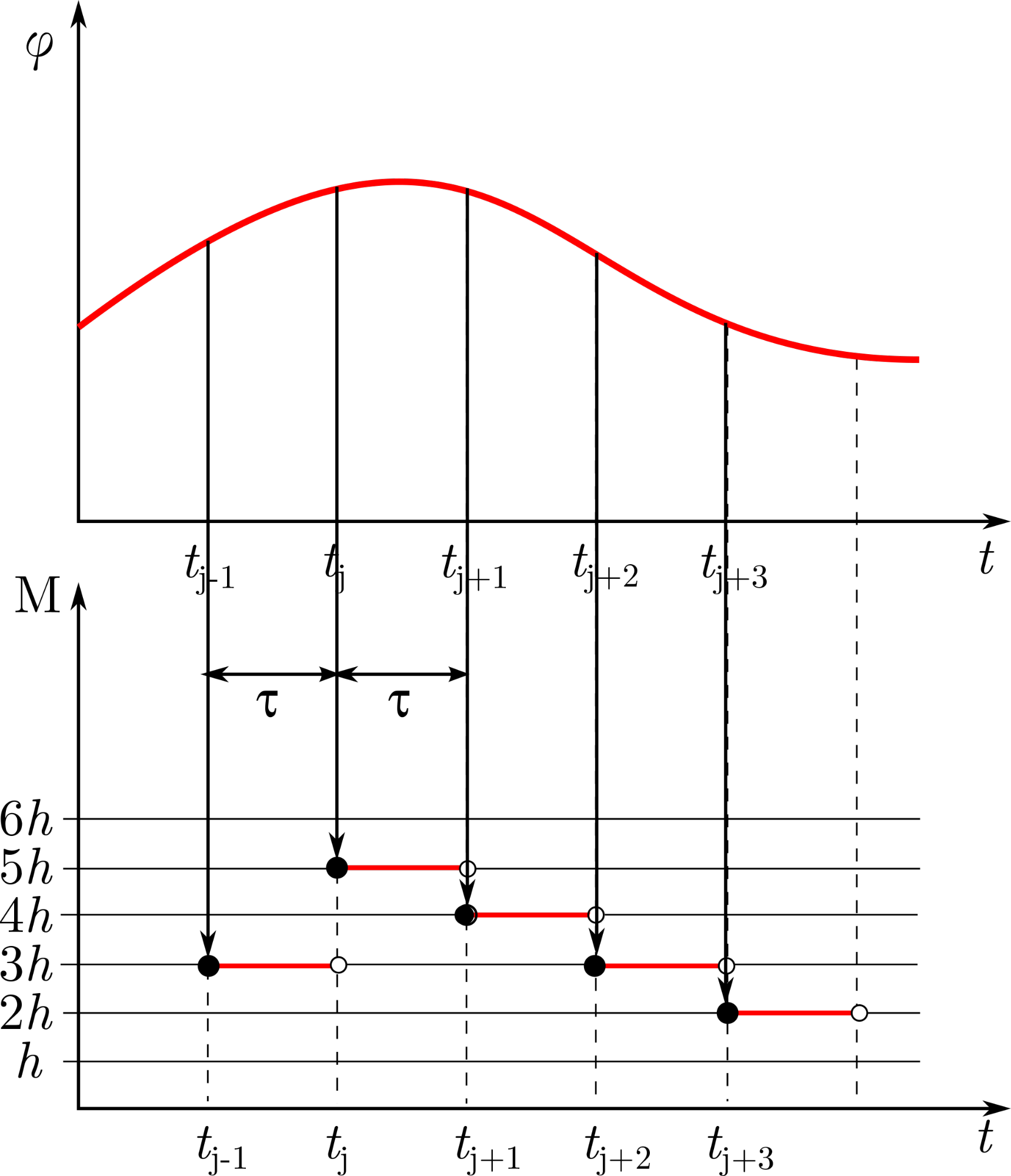
Figure 2.: The digitally controlled inverted pendulum [G1].
In this model, the computer periodically measures (samples) the position and angular velocity of the pendulum, then calculates the optimal control torque, which is applied with quantization (rounding). The control goal is the stabilization of the upright equilibrium.
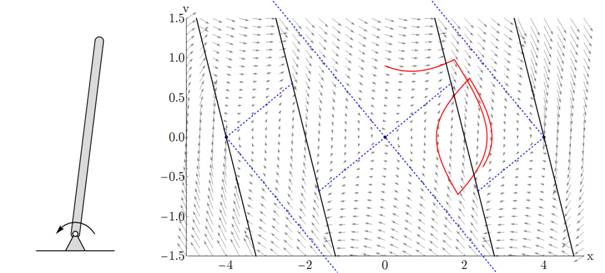
Plotting the pendulum’s movement on the position velocity phase space enables us to understand the reason of irregular oscillations.
Around the desired unstable equilibrium, the controller has a deadzone due to the rounding, that is, it does not apply control torque. Next to the deadzone, parallel bands correspond to specific control torque values, the bands are separated by switching lines (denoted by black lines)
As the pendulum starts to lean, the controller does not intervene until the pendulum reaches the band of the minimal control value. Then the controller pushes the pendulum back to the deadzone (where the control turns off again), and thus the pendulum moves back and forth between the two bands in the phase space.
Since the control does not monitor the pendulum continuously, it does not immediately detect when the pendulum reaches a different control band. This means that there is a random amount of time, for which the pendulum is allowed to move in an adjacent control band, before the next sampling instant occurs and the controller updates the value of the control moment.
This is illustrated by video 1, chaotic oscillation between the deadzone and the first control band can be observed, although later (after 1:00), it can be seen, that the random time before the sampling enables the pendulum to swing to the left side. A symmetric chaotic attractor is composed of the two repellers on the left and right side.
Video 1.: The phase-space of the digitally controlled inverted pendulum showing micro-chaotic behaviour
If we plot the states corresponding to sampling time instants with points, a fractal-like symmetric attractor reveals itself:
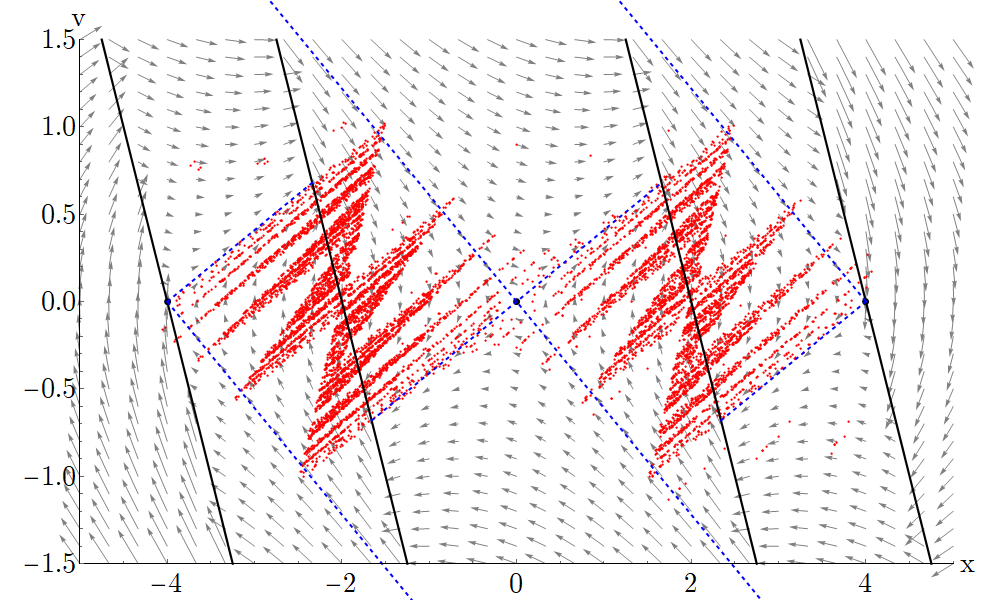
Figure 3.: The chaotic attractor covered by the motion in video 1.
It is clear, that even two digital effects (sampling and round-off) can lead to strange, chaotic oscillations and therefore may cause considerable control error.
In my research, I am seeking answer to the following questions.
● How is it possible to explore the phase space? How many attractors or repellers are present and what kind of attributes do they have?
● Is it possible to re-structure the phase space, so that the control error becomes smaller?
Methods
Analytical approach and simulations:
Micro-chaotic behaviour can be described by so-called micro-chaos maps [G2]. Specific properties of the map can be determined analytically, similarly the switching lines, equilibrium positions and the interaction of these can be examined with analytical approach.
With the aid of simulations, it can be seen, that not only the variation of system parameters, but the variation of the initial conditions can affect the micro-chaotic behaviour. For some initial conditions, the pendulum arrives at an attractor closer to the goal position, while for some others, it can arrive at an attractor further away (see Fig. 4), therefore the control error strongly depends on the initial state.
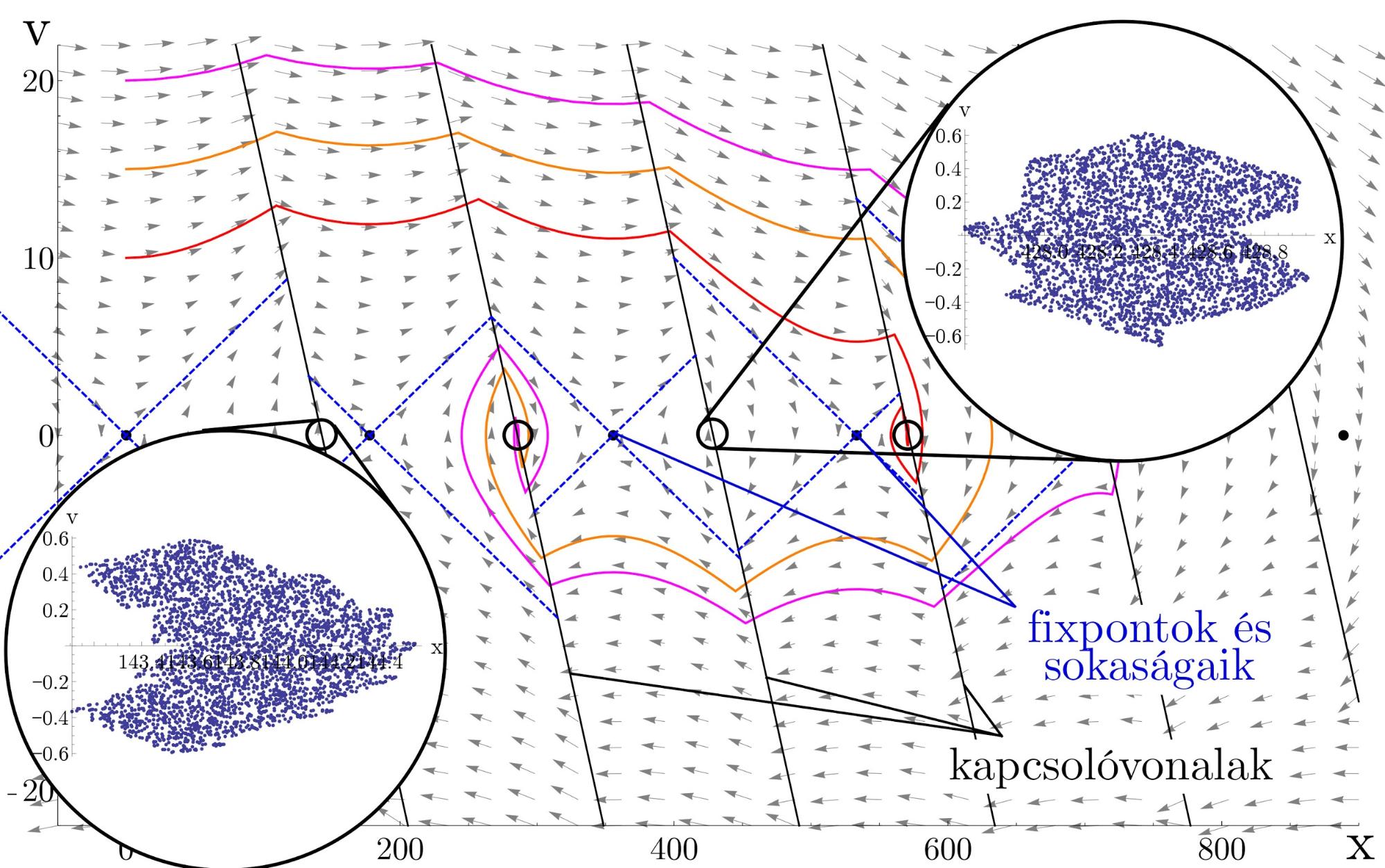
Figure 4.: The effect of initial conditions: depending on the initial velocity, the pendulum arrives at different attractors.
Examining the state space is not a straightforward task: with numerical simulations started from different initial conditions, it would be extremely time and computation power consuming, moreover in case of long transients, terminating the simulation too early would cause reasonable errors.
For this reason, I have used cell mapping methods (which were developed in the early 90’s), and they proved to be excellent for the task.
Cell mapping
During cell mapping, the phase space is discretized, subdivided into cells, and for every cell, one or more image cell is determined (where the dynamics lead to). In case of simple cell mapping (SCM), only one image corresponds to every cell, and by examining the chain of images, one can find periodic orbits, or transient cell-chains leading to periodic groups (see Fig. 5).
Chaotic attractors are typically covered by high-period cell groups and the transient cells leading to them correspond to the basin of attraction.

Figure 5.: Illustration of simple cell mapping (SCM). Every cell has a single image cell, and examining the chain of images allows one to discover periodic orbits (e.g. ABCD cells).
The computation time of cell mapping is linear with respect to the size of the examined phase space region; therefore it is orders-of-magnitude faster than running repeated simulations.
It can be challenging however, to select the region of the phase space to be examined, therefore I have extended the method and created clustered simple cell mapping, which is able to adaptively expand the phase space region, and also enables parallel execution [G3]. The clustered cell mapping is illustrated by Fig 6, where two simple cell mapping results are joined, and a new periodic group is found (orange cells in the middle), at the border of the two solutions.

Figure 6.: Illustration of clustered simple cell mapping: after adaptively expanding the state space region, the algorithm joins two SCM solutions and discovers a new periodic orbit. [G3]
Results
The results provided by cell mapping methods enabled me to prove several theories and assumptions originating from the analytical approach.
In case of the inverted pendulum, there is a pattern of saddle points and chaotic attractors, and by varying system or control parameters, this pattern can be altered. This can be utilized to tune parameters in a way, that chaotic attractors far from the desired position disappear (see Fig. 7).

Figure 7.: The phase space of the inverted pendulum in case of varying a system parameter. Initially there are 3-3 attractors on the left and right sides, finally there are 6-6 attractors. (Attractors are denoted by red spots surrounded by orange-yellow regions.)
I have scanned a wide range of system and control parameters with cell mapping, therefore the effect of changing specific parameters have been shown [G7]. I have utilized BUTE’s supercomputer to generate vast amount of cell mapping solutions.
In 2019 I have finished the open source package containing my implementation of cell-mapping algorithms (cell-mapping C++ library) which is capable of using multiple processors effectively. I have generated larger cell mapping simulations than ever before (using 4 billion cells), which show the global state space structure and fractal like attractors and basin boundaries at the same time.

Figure 8: (Click on the figure) 4 GigaPixel cell mapping result showing the state space of the micro-chaos map. Coloured regions indicate basin of attraction of fractal like, chaotic attractors situated at the x-axis.
I have shown that micro-chaotic behaviour can persist in case of Coulomb-friction [G5, G8]. The upright unstable equilibrium can be stabilized by the friction, however small perturbations can cause the pendulum to get to a chaotic attractor. (See Fig 9.)
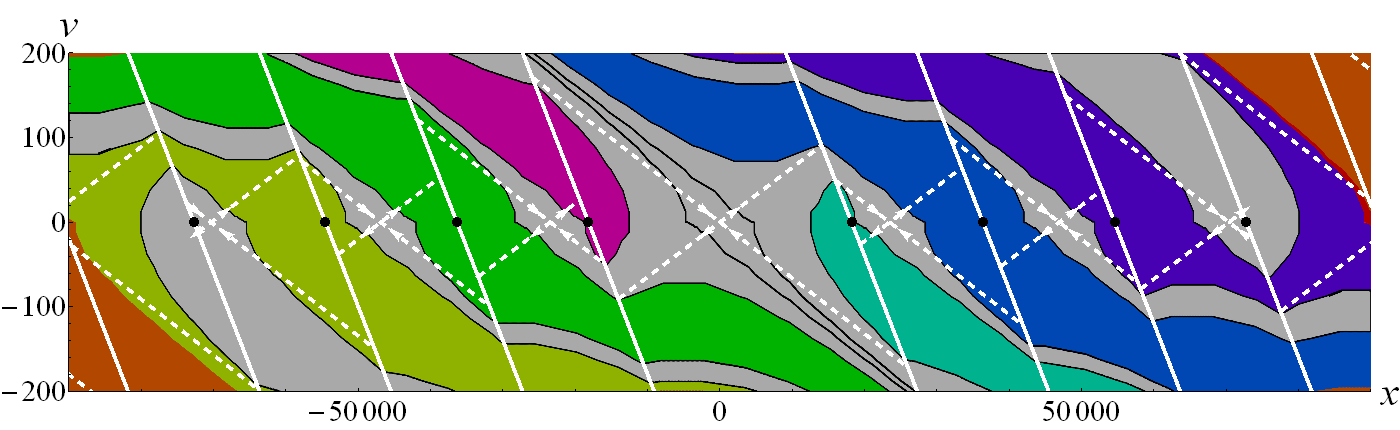
Figure 9.: The state space of the digitally controlled inverted pendulum with friction. Gray regions indicate sticking caused by the friction, coloured regions denote initial conditions which lead to chaotic attractors. [G5]
I have proved, that in specific rounding cases, periodic orbits with chaotic oscillations superposed appear in the state space [G6]. It could happen that multiple such periodic orbits are nested in each other, and a certain solution can be passed between them (see Fig. 10).
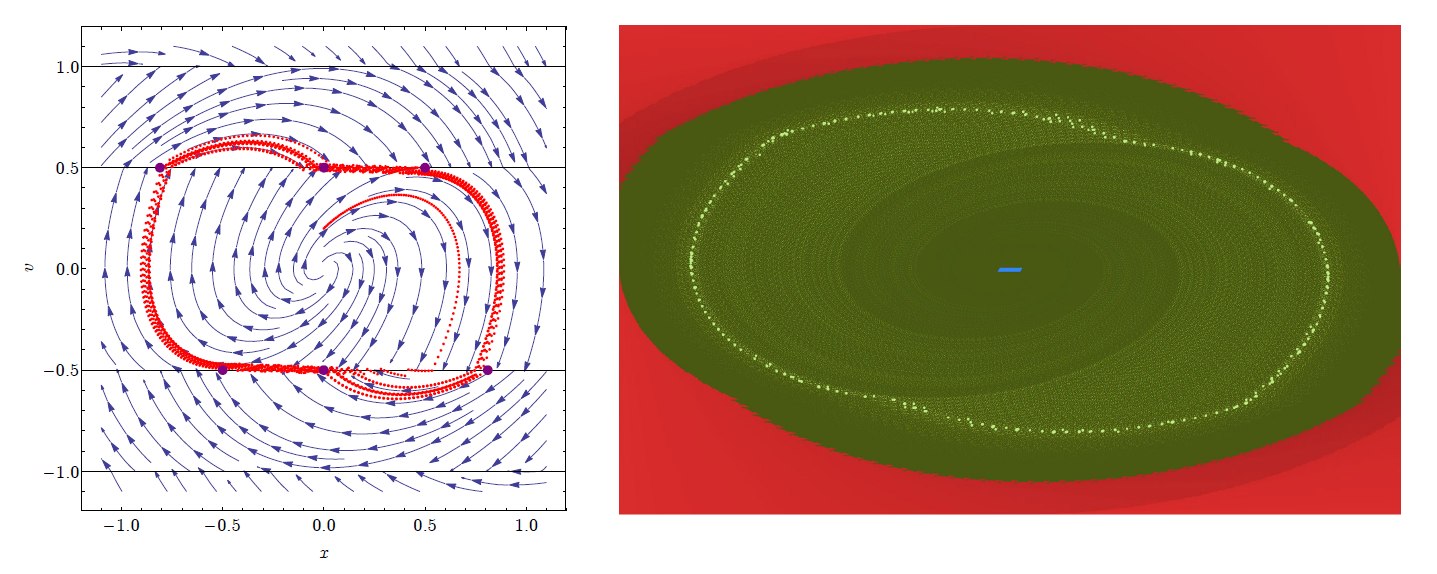
Figure 10.: Chaotic oscillations superposed on a periodic orbit (in case of D-control). Left: analytical solution, right: cell mapping results.
I have analysed the so-called twofold-quantization case (when both the measured signals and the control output is quantized), which fits the reality very well [G9].
Experiments have been carried out with direct-driven inverted pendulums utilizing microcontrollers and encoders (see Fig 11) [G5]. The newest generation of experimental device (along with the latest mathematical models) enabled me to record irregular motions which can be used to prove chaos experimentally as well. One of these measurements is shown on Fig 12 and Video 2.


Figure 11.: Two generations of the inverted pendulum experiment. 1: inverted pendulum, 2: motor with rotary encoder, 3: motor driver (H-bridge), 4: microcontroller.
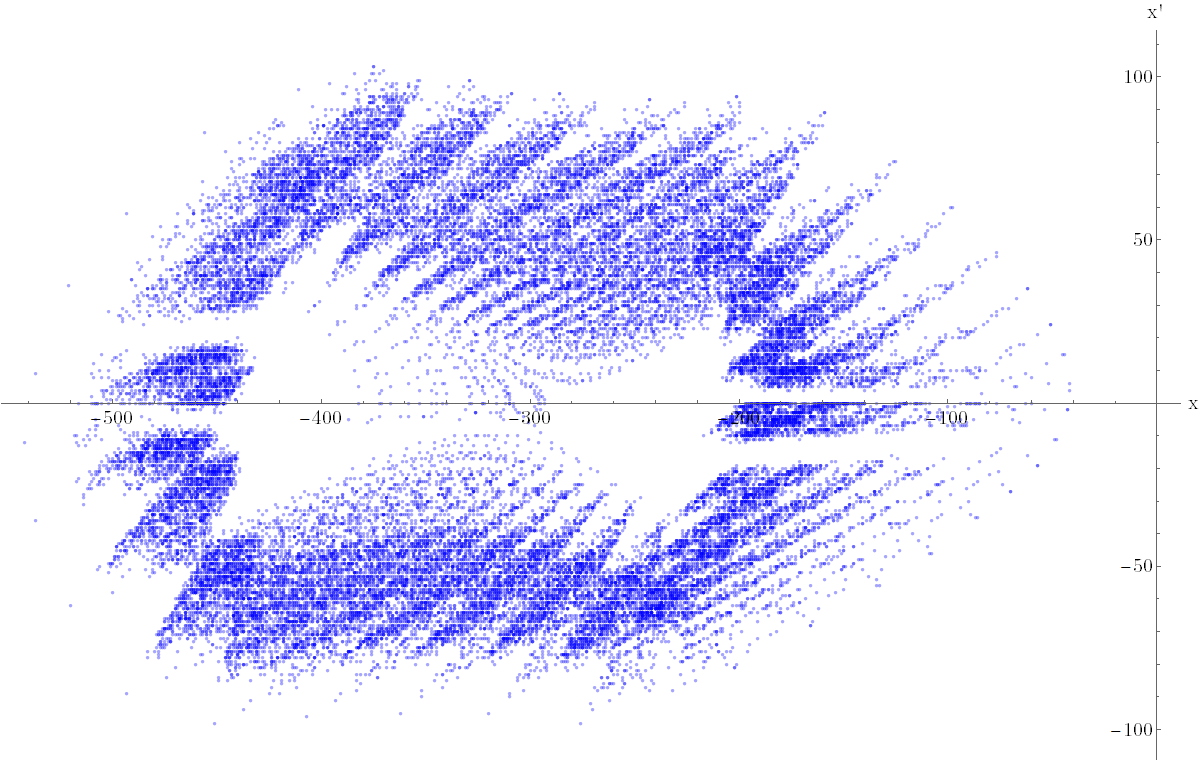
Figure 12: Experimentally obtained picture of a chaotic attractor. An unstable saddle point is situated in the middle of the chaotic attractor and its sawtooth-like fractal structure is clearly visible.

Video 2: Micro-chaotic oscillation in case of twofold-quantization (in case of artificially increased rounding resolutions). The measured position-velocity plot of the motion is shown on Fig. 12.
Expected impact and further research
One of the main impacts of my research is the popularization of cell mapping methods and the development of cell mapping techniques capable of examining micro-chaotic behaviour. In the age of multi-core processors and parallel computing, the adaptive clustered cell mapping will hopefully be a valuable tool for researchers analysing similar problems.
Moreover, it is extremely important to present micro-chaos phenomena to a wide audience. In practice, it is often neglected or replaced by random noise, although my results show, that doing so is often counterproductive.
The formalism of twofold-quantization in micro-chaos and taking friction into account enabled us to experimentally show the micro-chaotic behaviour. These results should provide foundation to further publications which will help popularize the field of micro-chaos.
Publications, references, links
List of corresponding own publications:
[G1.] Gyebrószki Gergely, Dr. Csernák Gábor: Digitális szabályozás okozta kaotikus rezgés amplitúdójának becslése, XII. Magyar Mechanikai Konferencia, (2015.08.25-27.), Miskolc, Hungary
[G2.] Dr. Csernák Gábor, Gyebrószki Gergely, Dr. Stépán Gábor: Multi-Baker Map as a Model of Digital PD Control, International Journal of Bifurcation and Chaos (IJBC), 26(2), 2016, pp. 1650023 1–11
[G3.] Gyebrószki Gergely, Dr. Csernák Gábor: Clustered Simple Cell Mapping: An extension to the Simple Cell Mapping method, Communications in Nonlinear Science and Numerical Simulation 42, 2017, pp. 607–622
[G4.] Gyebrószki Gergely, Csernák Gábor: Methods for the quick analysis of micro-chaos, Applied Nonlinear Dynamical Systems in Proceedings in Mathematics and Statistics in Springer Series (ISBN: 978-3-319-08265-3), 93 2014, pp. 383–395
[G5.] Gyebrószki Gergely, Csernák Gábor, Budai Csaba: Experimental investigation of micro-chaos, 8th European Nonlinear Dynamics Conference (2014.07.06–11), Vienna, Austria
[G6.] Gyebrószki Gergely, Nagy Péter Tamás, Csernák Gábor: Numerical Exploration of Micro-chaotic Behaviour, Finno-Ugric International Conference on Mechanics – 2013, book of abstracts
[G7.] Gyebrószki Gergely, Dr. Csernák Gábor: Inherent control error in a multi-PD controlled double inverted pendulum, Proceedings of the 9th European Nonlinear Dynamics Conference. 2017. pp. 238-1-238-5
[G8.] Gyebrószki Gergely, Dr. Csernák Gábor: The Hybrid Micro-chaos Map: Digitally Controlled Inverted Pendulum with Dry Friction, Periodica Polytechnica Mechanical Engineering, 63(2), pp. 148–155.
[G9.] Gyebrószki Gergely, Dr. Csernák Gábor: Twofold quantization in digital control: deadzone crisis and switching line collision, Nonlinear Dynamics, 2019. (submitted, under review)
Table of links:
- Amikor a robot keze megremeg: digitálisan szabályozott gépek kaotikus rezgései (Hungarian report about micro-chaos)
- Open access book on Chaos
List of references:
[1] Enikov, E., and Stépán, G., Micro-chaotic behavior of digitally controlled machines, in Proc. 15th ASME Biennial Conference on Mechanical Vibration and Noise (Boston, 1995).
[2] G. Haller, G. Stépán: Micro-chaos in digital control, Journal of Nonlinear Science, 1996, Volume 6, Number 5, Page 415
C.S. Hsu: Cell-to-Cell Mapping: A Method of Global Analysis for Nonlinear Systems, Applied Mathematical Sciences 64, 1987, Springer, Singapore
