Doctoral School of Mathematics and Computer Science  

BME TTK, Department of Geometry

Supervisor: Dr. Szirmai Jenő

Regular Horosphere Packings in Hyperbolic Spaces

Introducing the research area

I investigate the structure of Bolyai-Lobachevsky or hyperbolic geometry, the spaces of constant negative curvature, the discovery of which is attributed to the Hungarian mathematician János Bolyai. “I created a new world out of nothing…” wrote Bolyai in his letter to his father informing him of his discovery, on November 3rd, 1823. My research topic, as we shall see, is well embedded in the history of Hungarian mathematics, and I would like to contribute to this enterprise.

 

My topic of optimal ball packing problems aims to answer the question of which arrangements of balls yield the densest possible packing in a given space, so that no two balls overlap. In my research I study sphere packings in n-dimensional hyperbolic spaces, and investigate horoball packings, an important class balls, in dimensions n = 3,…,9.

 

Brief introduction of the research place

The Geometry Department at the Mathematics Institute of the Budapest University of Technology and Economics hosted my research, and I was supervised by Dr. habil. Jenő Szirmai. The Geometry Department, as a successor to the Descriptive Geometry Department founded by Professor Gyula Strommer is currently involved in a wide range of geometry research, from the geometrical physics to the study of Euclidean and non-Euclidean discrete geometry.

 

History and context of research

According to Thurston’s Geometrization conjecture the universe around us can be described by eight geometries, the maximal homogeneous Riemannian geometries, known as the Thurston Geometries. These include the three spaces of constant curvature, namely Euclidean, spherical, and hyperbolic space, as well as other more exotic spaces. The study of all eight geometries is important; they determine how crystalline structures can grow, and the configurations in which atoms arrange themselves. In the materials science context we model atoms using balls, and study which ball configurations arise in a given space. The geometric groups acting on a space describe all its possible symmetries. In Euclidean space 230 such space groups (crystallographic groups) can exist, and the packings associated with them have been thoroughly studied. The question of optimal ball packings is still mostly open in the other Thurston Geometries [Sz], not to mention higher dimensional hyperbolic spaces [Sz07, Sz13].

 

We mention two surprisingly new results in the topic:

 

• The origin of ball packing problems is the Kepler Conjecture in regular Euclidean 3-dimensional space, named after Johannes Kepler. In his 1611 book entitled The Six Cornered Snowflake, he conjectured that the densest possible congruent ball packing has a density of approximately 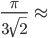74%. This conjecture was only proved in 1998 by Thomas Hales using results of Laszló-Fejes Tóth, using a modern computer assisted proof [H].

 

• Another new result by M.S. Viazovska from 2016 is that in the 8-dimensional Euclidean space the densest ball backing is that associated to the 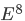 lattice [V].

 

Featured applications of ball packing in computer science include theory of error correcting codes. Here redundancy is added to the codes passing through a channel, and this requires optimizing the distance between the code words modeled by “balls” resulting in a packing.

 

Research goal, open questions

Hyperbolic space admits three types of spheres: regular sphere, horosphere, and hypersphere. The goal of my research is to investigate the best possible ball packings in n-dimensional hyperbolic geometry using horospheres. In dimensions 2-3 the best possible packings are given by horospheres [FTL], [BF]. We define packing density relative to the Dirichlet-Voronoi cells of the packing, which coincide with the fundamental domains of the symmetry groups.

 

In hyperbolic space the so called Böröczky-type simplicial packing density upper bound holds. This result, according to Károly Böröczky Sr., states that the locally optimal packing density using balls of radius r is attained by placing n+1 balls at the vertices of a regular simplex with edge length 2r [B, K98]. In 3-dimensional hyperbolic space, the monotonicity of the simplicial packing density function  with n=3 is known, i.e. the local packing density increase as a function of the radius r of the balls in the packing. (Note that this is caused by the negative curvature; in Euclidean spaces this density is independent of r.) Based on this monotonicity, it has been proved that the locally densest ball packing is realized in the limit by balls of infinite radius, also known as horospheres or horoballs, centered at the vertices of a regular tetrahedron with all vertices at the boundary of our space, see Fig. 1(a). Coincidentally the totally asymptotic regular tetrahedron tiles hyperbolic 3-space, and this upper bound is tight, yielding packing densities of approximately 85.3%, however not with classical balls, but with limiting horoballs centered at the boundary of the space [BF]. See Fig. 1 (b) for an illustration of this case in the Cayley-Klein model.

 

 

            

                               (a)                                                                          (b)

 

Fig. 1: The Böröczky-type optimal packing configuration in the Cayley-Klein ball model of 3-dimensional hyperbolic space. (a) Four congruent horospheres in the asymptotic regular simplex (tetrahedral) fundamental domain. (b) Image of the packing generated reflections on sides of the fundamental domain.

 

Every horosphere is congruent, there exists a hyperbolic isometry taking one to another. We introduced the notion of “horoball type” with respect to a fundamental domain of the tiling to differentiate between horoballs of a tiling. This opened new directions in the study of horopshere packings, and as my co-author recently showed, it is possible to construct locally optimally dense ball packings using horoballs of different types yielding higher densities than if we restricted ourselves to horoballs of the same type [Sz12]. Thus to understand regular packings in hyperbolic space it is important to analyze horoball packings of Coxeter tilings with asymptotic vertices. Such Coxeter tilings (also known as Koszul or paracompact tilings) only exist for dimensions n = 2,…,9 and there are only finite number of them for dimensions n ≥ 3, furthermore their volumes were recently found [JRKT, JKR]. In our research, we completed investigations of horoball packings in all dimensions where they exist, and in each dimension we found the densest known packings.

 

Methods

 

Our method of investigation rests on two tools. We use the projective model of hyperbolic geometry, an apparatus developed by our research group [Mo]. We developed a software package for computing horoball packing densities of hyperbolic space of any dimension. For implementation we use Mathematica, which assist in symbolic and numerical computations.

 

In addition to reviewing the relevant mathematical literature support by software packages were crucial. These enabled us to simplify and execute complex computations, as well as visualize the packings found in theory.

 

Foundational results can be derived from the work of László Fejes Tóth and also of Károly Böröczky Sr., who (the latter) proved that the notion of packing density is critical in hyperbolic space and depends on cellular decompositions [FKK]. This situation is related to the Banach-Tarski paradox. Higher dimensions are better behaved; in our work we compute packing densities based on the Dirichlet-Voronoi cells of the packing to avoid such paradoxes.

 

László Fejes-Tóth and H.S.M. Coxeter conjectured that the locally densest packings using balls of radius r have balls centered at the vertices of a regular simplex. In two dimensions L. Fejes Tóth proved this conjecture, while in hyperbolic 3-space it was shown in 1964 by K. Böröczky Sr. and A. Florian [BF].

Based on their results, we investigated all possible horopshere packings related to the asymptotic Coxeter simplices in dimensions 3 through 9 with our new method, and got surprisingly good results.

 

 

Results

Our main result is that in each dimension in which Coxeter tilings exist, we were able to produce the densest known packings. In dimensions  our packings are the densest known, while for we discovered new optimally dense packings using horospheres. In the case of  we were able to disprove a conjecture of László Fejes Tóth, that the optimal packing density equals , by producing a counterexample with higher density.

 

The following table summarizes our results. The theoretical packing density upper bound given by the simplicial density function is denoted as , and  gives the difference of the examples from our construction.

 

 

3-dimensional hyperbolic space

 

Our main result in 3 dimensions is the nonuniqueness of the optimal packing configuration; we constructed optimal horoball packings that have packing densities that agree with the Böröczky-type upper bound, but have symmetries different from the classical result. We introduced the notion of horoball type, the ratio of the horoball volume with respect to a fundamental domain, to describe these packings. The animation in Fig. 2. (a) shows the possible horoball types in the (tetrahedral) fundamental domain [Sz05,KSz1,KSz3,KSz4], while Fig 2. (b)-(c) is our new packing, the extremal case.

 

 

              

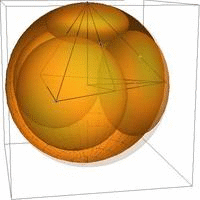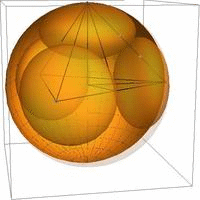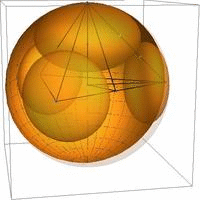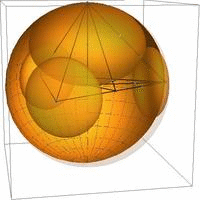
                         (a)                                                                            (b)                                               (c)                                                                  

 

Fig. 2: (a) Transition from the Böröczky-type optimal ball packing (starting state) into our new optimal horosphere packing (final state), (b) Our new optimal horosphere packing of the asymptotic simplex tiling in the fundamental domain and (c) reflected in hyperbolic space.

 

 

 

4-dimensional hyperbolic space

 

Here we constructed a class of horosphere packings that have higher packing densities than the conjectured packing density upper bound of 0.690... set by László Fejes Tóth in his book Regular Figures [FTL]. Our current best packing density is approximately 0.71644896… The range of the optimal packing density is .

 

 

 

5-dimensional hyperbolic space

 

There are 12 Coxeter simplex tilings in 5-dimensional hyperbolic space, we again give new packing density lower bounds and restrict the range of optimal ball packing densities to range  See Fig. 3, [Ksz5].

 

 

 

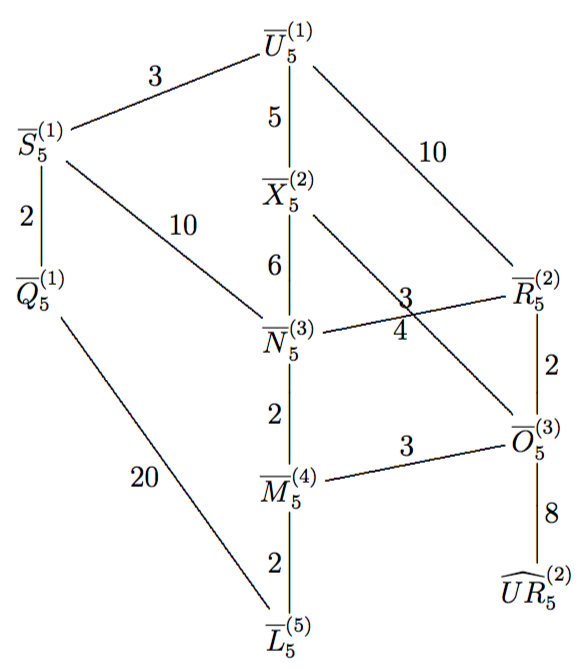
Fig. 3: Lattice of subgroups of the 5-dimensional Coxeter simplex groups; data of the 12 cases, volumes are in terms of the Riemann Zeta function.

 

6-9-dimensional hyperbolic space

 

The analysis of these cases [KSz6] was supported by  the UNKP-18-3 New National Excellence Program of the Hungarian Ministry of Human Capacities. For the best known packing densities see the table above.

 

Expected impact, further research

 

We presented our results at multiple international conferences, twice at the Rényi Institute of Mathematics at the Hungarian Academy of Sciences (HAS): László Fejes Tóth’s Centennial birthday conference, and the 70th birthday conference in honor of Imre Bárány, both Hungarian academicians, with proceedings [K1]. We presented at Discrete Geometry Days 2016 and 2019, a conference organized at BUTE. Internationally, we presented at the Berlin Mathematical School Discrete and Convex Geometry summer school, and the Symmetry Festival organized at TU Wien. Selected publications appeared in the Journal of Discrete and Computational Geometry, and Monatshefte für Mathematik. Independent citations include applications to knot theory [C], and the Wikipedia article on sphere packings.

 

We plan to extend our research to other Thurston geometries, and in our future work we plan to develop the connection to dynamical systems through analytic number theory, arithmetic groups and Kleinian groups [KD].

 

 

Publication, references, links

My Publications

 

[K1] Kozma, R.T., Dense regular horoball packings in higher dimensional hyperbolic spaces, Discrete Geometry and Convexity in honour of Imre Bárány, Eds. Ambrus G., Böröczky K.J., Füredi Z., pp. 143–144, Budapest, Hungary (2017). ISBN 978-963-279-963-6

 

[KSz1] Kozma R. T., Szirmai J. Symmetries of Horoball Packings Related to Famous 3-dimensional Hyperbolic Tilings, Symmetry: Culture and Science, Volume 27, No. 4, pp 261–278 (2016).

 

 [KSz2] Kozma R. T., Szirmai J. New Lower Bound for the Optimal Ball Packing Density in Hyperbolic 4-space, Journal of Discrete and Computational Geometry, Volume 53, Issue 1, pp 182–198 (2015).

 

 [KD] Kozma, R. T., Devaney, R. L. Julia Sets Converging to Filled Quadratic Julia Sets, Journal of Ergodic Theory and Dynamical Systems, Volume 34, Issue 01, pp. 171–184 (2014).

 

[KSz3] Kozma, R. T., Szirmai J. Optimally Dense Packings for Fully Asymptotic Coxeter Tilings by Horoballs of Different Types, Monatshefte für Mathematik, Volume 168, Issue 1, pp. 27–47 (2012)

 

[KSz4] Kozma, R. T., Szirmai J., Structure and Visualization of Optimal Horoball Packings in 3-dimensional Hyperbolic Space, ArXiv:1601.03620. (Submitted)

 

[KSz5] Kozma, R.T., Szirmai J., New Horoball Packing Density Lower Bound in Hyperbolic 5-space. (in publication, Geometriae Dedicata)

[KSz6] Kozma, R.T., Szirmai J., Optimal Horoball Packing Densities for Coxeter Simplex Tilings in Hyperbolic n-space for n=6,7,8,9. (Preprint)

 

Collection of Links

 

BUTE Mathematics Institute

BUTE Geometry Department

Dr. Jenő Szirmai’s homepage

My personal home page with figures and Mathematica code

Wikipedia page on sphere packings mentioning our results

Wolfram Demonstrations Project page featuring our figure of the [3,3,6] case

 

References

[B] Böröczky,K. Packing of spheres in spaces of constant curvature, Acta Math. Acad. Sci. Hungar., 32 (1978), 243–261.

[BF] Böröczky, K. Florian, A. Über die dichteste Kugelpackung im hyperbolischen Raum, Acta Math. Acad. Sci. Hungar., 15 (1964), 237–245.

[C] Adams, Colin, et al. Densities of hyperbolic cusp invariants of knots and links. Proc. Amer. Math. Soc. (2018).

[H] Hales, T. C. Historical Overview of the Kepler Conjecture, Discrete and Computational Geometry, 35 (2006), 5–20.

[FKK] Fejes Tóth, G. Kuperberg, W. Kuperberg, Packing and Covering with Convex Sets, Handbook of Convex Geometry, Volume B, eds. Gruber, P.M., Willis J.M., pp. 799-860, North- Holland, (1983).

[FTL] Fejes Tóth, L. Regular Figures, Macmillian (New York), 1964.

[JKRT] Johnson, N.W., Kellerhals, R., Ratcliffe, J.G., Tschants, S.T. The Size of a Hyperbolic Coxeter Simplex, Transformation Groups, 4/4 (1999), 329–353.

[JKRT2] Johnson, N.W., Kellerhals, R., Ratcliffe, J.G., Tschants, S.T. Commensurability classes of hyperbolic Coxeter Groups, Linear Algebra and its Applications, 345 (2002), 119–147.

[K98] Kellerhals, R. Ball packings in spaces of constant curvature and the simplicial density function, Journal für reine und angewandte Mathematik, 494 (1998), 189– 203.

[Mo] Molnár, E. The Projective Interpretation of the eight 3-dimensional homogeneous geometries, Beitr. Algebra Geom., 38/2 (1997), 261–288.

[Sz05] Szirmai, J. The optimal ball and horoball packings of the Coxeter tilings in the hyperbolic 3-space Beitr. Algebra Geom., 46/2 (2005), 545–558.

[Sz07] Szirmai, J. The optimal ball and horoball packings to the Coxeter honeycombs in the hyperbolic d-space Beitr. Algebra Geom., 48/1 (2007), 35–47.

[Sz12] Szirmai, J. Horoball packings and their densities by generalized simplicial density function in the hyperbolic space, Acta Math. Hung., 136/1-2 (2012), 39–55, DOI: 10.1007/s10474-012-0205-8.                 

[Sz13] Szirmai, J. Horoball packings to the totally asymptotic regular simplex in the hyperbolic n-space, Aequationes Mathematicae, 85 (2013), 471-482, DOI: 10.1007/s00010-012-0158-6.

[V] Viazovska, M. S. "The sphere packing problem in dimension 8." Annals of Mathematics 185, no. 3 (2017): 991-1015.