|
|
BMe Research Grant |
|
Doctoral School of Electrical Engineering
BME VIK, Department of Automation and Applied Informatics
Supervisor: Dr. Vajk István
Optimization Methods for Motion Planning in Robotics
Introducing the research area
Robots have become increasingly widespread nowadays. They play an essential role in our life. My research is related to a partial problem of robotics, which belongs to motion planning. Motion planning plays one of the most important roles for both industrial and commercial applications in robotics. Motion planning focuses on planning collision-free motion from a start to a goal position among obstacles. The complete problem can be highly complex. Therefore, a popular solution is to decouple the problem into planning and timing steps. First, a geometry planner determines a path considering geometric constraints. In the next step, a velocity profile for the predefined path is generated. The second step is often called path tracking. My research focuses on the second step of the decoupled approach.
Brief introduction of the research place
My work is carried out at the Robotics Research Group of the Department of Automation and Applied Informatics under the supervision of Dr. Vajk István. The research group focuses on navigation and control for mobile and industrial robots. Besides theoretical work, the group created several pilot projects, for example, a robotic demonstration with 5G network at the 2016 Mobile World Congress in Barcelona, or a Virtual Reality (VR) controlled car-like robot in 2019.
History and context of the research
In the decoupled planning approach, the path of the geometrical planner cannot be applied to the robot, since the path does not contain any time information [H2]. Also, some constraints of the robot (e.g., dynamics) are ignored during the first step. Therefore, a second step (path tracking) is necessary, in which a velocity profile is generated for the given path. The path tracking can have various goals (e.g., minimum-time, minimum-energy). In my work, I only investigate minimum-time path tracking problems.
Time optimal control plays an important role in a wide range of applications, including aerospace tasks, material handling, and industrial processes [H3]. Path tracking methods can increase productivity in these applications by optimizing the motion of the robot. In some cases, the time-dependency is not specified, which means the motion of the given task is only partially determined. Optimal algorithms can exploit this degree of freedom and increase efficiency without violating any constraint of the system.
The research goals, open questions
Time-optimal path tracking is still an active topic in robotic research [H4]. The aim of my work is to extend this research area by creating algorithms that can solve the control problem significantly faster than the existing methods in the literature. My secondary goal is that these algorithms do not tighten the possible constraints of the system, and therefore, they can be considered as a fully usable alternative to the existing approaches.
Methods
Generally, there are three different approaches to solve the path tracking problem of the decoupled minimum-time control approach [H3]. Dynamic programming approach divides the state space into a discrete grid, and the optimal solution is found in this plane. Indirect methods are based on the necessary optimality conditions of the time-optimal control program. In contrast, direct approach solves the problem by creating a finite-dimensional approximation of the original optimal problem. Nowadays, the direct approach is the most widespread and suitable solution for path tracking in real-time applications [H1,H3].
My contributions are also based on direct methods. Direct approaches transform the infinite dimensional problem to a finite non-linear optimization problem, which can be solved using existing optimization tools. The benefit of the direct approach is that these solver methods can easily deal with inequality, equality constraints, and parameter changes.
As we have seen above, direct methods are based on mathematical optimization algorithms. Mathematical optimization corresponds to the problem of choosing the best possible vector from a set of candidate choices. An objective function represents the cost of choosing the vector. Convex optimization is a subfield of mathematical optimization, which is used in many applications from control theory, signal processing to finance and portfolio optimization. The robotic path tracking problem was also formed using a convex, second order (SOCP) program [H3].
My research also starts from the SOCP formulation. I have defined a new optimization technique called peaked concept [F4,F5]. A non-linear optimization program with strictly monotone decreasing objective function, and with special constraint set (peaked set) can be solved faster than the original problem. A simple, peaked set can be seen in Figure 1. The constraint set of the SOCP program is not peaked. However, I have introduced an alternative discretization method, which leads to a peaked problem [F2]. Due to the peaked reformulation, the SOCP program can be solved using a linear, LP problem. The benefit of the LP problem is the lower computational time.
The LP formulation can be solved nearly one order of magnitude faster than the SOCP problem. Furthermore, if we exploit the banded, sparse structure of the problem, the runtime difference can be higher compared to the state-of-art solver algorithms. For this purpose, I created a sequential solver method for banded peaked problems [F4,F5]. Based on experimental results, the sequential solver outperforms the examined algorithms by two orders of magnitude.
Convex reformulation fails to address some practical constraints for time-optimal path tracking (e.g., torque rate constraints, velocity-dependent torque characteristics, jerk constraints) since these applications introduce terms that destroy the convexity. In this case, non-convex solvers can be applied to the problem. However, the computational demand of these methods is high and exponential in the path size. This can result in that the path-tracking program can be solved in case of a limited path length. To address this problem, I introduce a special formulation, which can be applied to the non-convex program even in real-time applications [F1,F3]. The major intuition behind the approach is that using the formulation, the local optima of the time-optimal problem are also global optima. In contrast, a global optimization method has to perform local optimization thousands of times to provide a global optimum point.
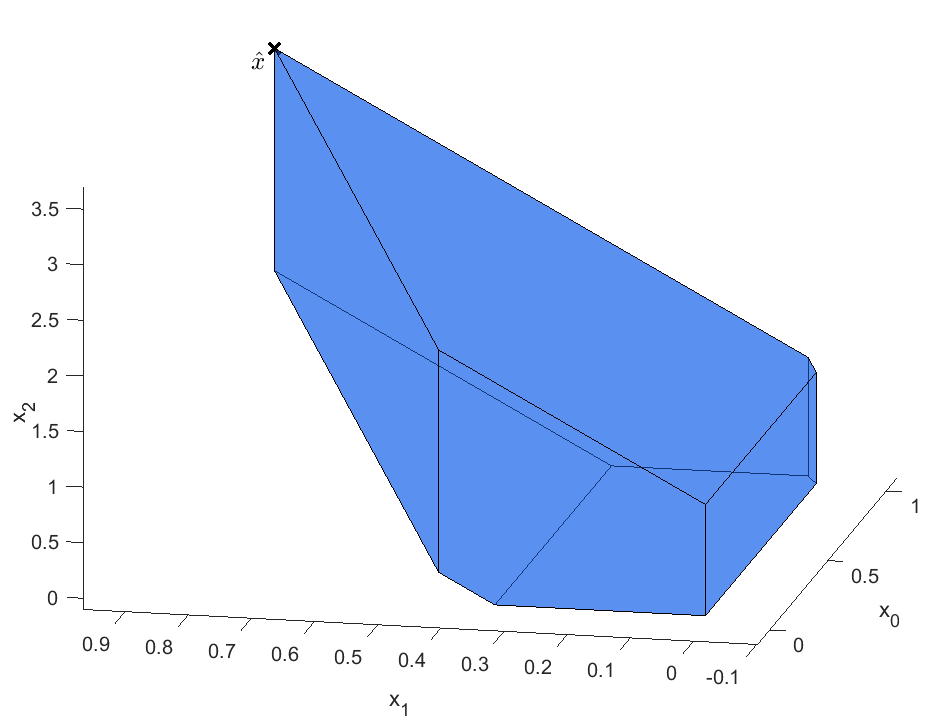
Figure 1: A simple, three-dimensional peaked set.
Results
The presented methods solve the time-optimal path tracking problem significantly faster than any other algorithm in the literature. The runtime results of the examined solvers can be seen in Figure 2. Based on these results, we can see that the sequential solver outperforms the second Gurobi LP method by nearly two orders of magnitude. Gurobi is a state-of-art commercial solver, which is used by major companies (e.g., Google, Toyota, and Microsoft) and research institutes. Besides Gurobi, a specific method (MTSOS) for the minimum-time path tracking problem is examined, which is written by Thomas Lipp in Stephen Boyd's lab at Stanford University
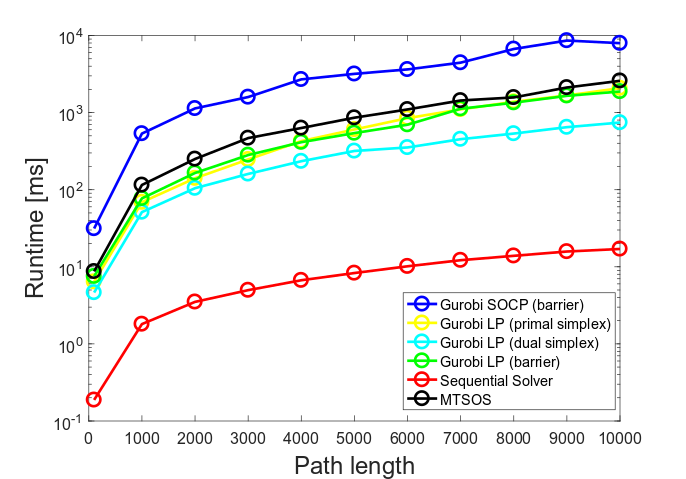
Figure 2: Runtime results of the examined solver approaches for various path lengths.
The presented algorithms are published in highly ranked journals [F1-F5]. We also created several experimental scenarios, where the methods are demonstrated and validated using a robotic manipulator. As a practical example of the path tracking application, we solved the waiter motion problem (see Figure 3). The problem consists of moving a tablet carrying one or more glasses along a prescribed spatial path as fast as possible so that the objects placed on it do not slide. A closely related problem is the pick-and-place task with suction cups, which is used in logistics and other industrial applications.

Figure 3: The waiter motion problem using a six degree-of-freedom robotic arm.
Another application of the path tracking problem is related to a Japanese robotics company. The company offers vision based solutions for industrial robots, and its products have been installed in many factories. Their solutions can perform object recognition and pose estimation in three dimensions. Based on the presented sequential solver, we developed a custom software for the company, which solves the path tracking problem. The software can cooperate with Robot Operating System (ROS), which is a popular robotic platform. The program can handle various constraints, including end-effector and joint limitations. In Figure 4, an example application can be seen, where the velocity profile is generated using the sequential solver. The software development was performed in the frame of a contract between BME and the company (contract registry number is AUT 2019, 411.175/2019).

Figure 4: An example scenario using the solution of the Japanese robotic company. The robot performs a pick-and-place task using a vision system. The velocity profile of the trajectory is generated by the sequential solver.
Expected impact and further research
Time-optimal path tracking is still an active topic in robotic research, and several papers are published recently about the topic [H4]. At the beginning of 2019, we extend the sequential solver in collaboration with a research group from the University of Parma [F5]. Related to this work, researchers of the Massachusetts Institute of Technology prove some theoretical property of the extended sequential solver [H6].
As a future research direction, I will use the presented new methods for geometrical path planning. The runtime of the sequential solver is very low. It can provide the travel time for the given path considering the dynamic constraints in less than 1 ms. Therefore, the solver can be used during the path planning stage. In this case, we get a coupled motion planning approach, since the geometrical and the dynamic constraints are taken into account together.
Publications, references, links
Related journal papers:
[F1] Á. Nagy, G. Csorvási, I. Vajk. “Path Tracking Algorithms for Non-Convex Waiter Motion Problem”. In: Periodica Polytechnica Electrical Engineering and Computer Science 62.1 (2018), pp. 16–23.
[F2] Á. Nagy, I. Vajk. “LP-based velocity profile generation for robotic manipulators”. In: International Journal of Control 91.3 (2018). IF*: 2.101, pp. 582–592.
[F3] Á. Nagy, I. Vajk. “Non-Convex Time-Optimal Trajectory Planning for Robot Manipulators”. In: Journal of Dynamic Systems, Measurement, and Control (2019). IF*: 1.521, in press
[F4] Á. Nagy, I. Vajk. “Sequential Time-Optimal Path Tracking Algorithm for Robots”. In: IEEE Transactions on Robotics (2019). IF*: 4.264. in press
[F5] L. Consolini, M. Locatelli, A. Minari, Á. Nagy, I. Vajk. “Optimal Time Complexity Speed Planning for Robot Manipulators”. In: IEEE Transactions on Robotics 35.3 (2019). IF*: 4.264, pp. 790–797.
Related conference papers:
[K1] Á. Nagy, I. Vajk. “Validating Time Optimal Path Tracking Algorithm for Robots”. In: Proceedings of the Automation and Applied Computer Science Workshop 2016: AACS’16. 2016, pp. 141–149.
[K2] Á. Nagy, I. Vajk. “Minimum-time path tracking for robots with non-convex constraints”. In: 2017 IEEE 15th International Symposium on Intelligent Systems and Informatics (SISY). 2017, pp. 163–168.
[K3] Á. Nagy, I. Vajk. “Peaked Optimisation Problem for Motion Planning in Robotics”. In: Proceedings of the Automation and Applied Computer Science Workshop 2017: AACS’17. 2017, pp. 147–156.
[K4] G. Csorvási, Á. Nagy, I. Vajk. “Near Time-Optimal Path Tracking Method for Waiter Motion Problem”. In: 20th World Congress of the International Federation of Automatic Control. 2017, pp. 4929–4934.
List of references:
[H1] Thomas Lipp, Stephen Boyd. “Minimum-time speed optimisation over a fixed path”. In: International Journal of Control 87.6 (2014), pp. 1297–1311.
[H2] B. Siciliano, O. Khatib. “Springer Handbook of Robotics”. Springer-Verlag Berlin Heidelberg, 2008.
[H3] D. Verscheure, B. Demeulenaere, J. Swevers, J. Schutter, M. Diehl. “Time-Optimal Path Tracking for Robots: A Convex Optimization Approach”. In: IEEE Transactions on Automatic Control 54.10 (2009), pp. 2318–2327.
[H4] H. Pham, Q. Pham. “A New Approach to Time-Optimal Path Parameterization Based on Reachability Analysis”. In: IEEE Transactions on Robotics 34.3 (2018), pp. 645–659.
[H5] F. Debrouwere, W. Van Loock, G. Pipeleers, Q. T. Dinh, M. Diehl, J. Schutter, J. Swevers. “Time-Optimal Path Following for Robots with Convex-Concave Constraints Using Sequential Convex Programming”. In: IEEE Transactions on Robotics 29.6 (2013), pp. 1485-1495.
[H6] I. Spasojevic, V. Murali, S. Karaman. “Asymptotic Optimality of a Time Optimal Path Parametrization Algorithm”. Version 1. 2019. arXiv: 1904.04968 [cs.RO]
