|
|
BMe Research Grant |
|
Doctoral School of Electrical Engineering
BME-VIK, Department of Control Engineering and Information Technology
Supervisor: Dr. HARMATI István
Evaluating semi-cooperative Nash/Stackelberg Q-learning for traffic routes plan in a single intersection
Introducing the research area
In the urban transportation system, the existing traffic infrastructure and control system cannot meet the demand for growing traffic, resulting in frequent traffic congestions. Due to limited funds and resources, the cost-effective implementation of intelligent self-optimization systems and low-cost controllers in a real transport system is preferred to infrastructure reconstruction. The most common traffic light control strategy in the real world is the constant strategy, i.e., the time intervals of traffic lights are fixed and periodic resulting in inefficient traffic flow control. Therefore, a self-adaptive traffic signal control system is developed that offers a more efficient solution in the traffic management system and generates flexible strategies to control traffic flow via collecting and analyzing real-time data from the traffic environment.
Brief introduction of the research place
The research work takes place out in a laboratory room provided by the Department of Control Engineering and Information Technology (IIT) of BUTE. Our department aims to persist in embracing and contributing to the latest advances in its competence domains, including the newest technologies related to the application of GPGPUs and artificial intelligence in visualization and image processing, development of GRID and cloud-based services, Industry 4.0 technologies, collaborative robotics to name a few.
History and context of the research
The integration of artificial intelligence theories into the control of traffic lights is quite popular in current self-adaptive traffic light control systems. The traffic signal timing plan or the traffic management system can be rescheduled by the fuzzy logic rules based only on the local information [1]. Genetic algorithms, Ant Colony Optimization, and Particle Swarm Optimization are widely used to mimic biological social behavior [2]. The problem of traffic optimization can be transformed into a problem of game theory, where inbound links are considered players and the control of traffic lights is the decision of these players [3].
The machine learning-based self-adaptive traffic signal control system has self-learning capabilities and high-efficiency computing capabilities in traffic control problems. It learns the traffic knowledge from the empirical information in the traffic environment to make optimal decisions to control traffic. Reinforcement learning (RL) methods are suitable for implementation in such a complex environment of traffic transportation systems [4]. Earlier work presented a simple case for the isolated traffic signal control, which involves the application of RL to demonstrate efficiency [5]. Multi-agent reinforcement learning (MARL) is an extension of RL, where each traffic light can be constructed as an agent and light control is considered the actions taken by the agents. Multiple agents learn the policies to determine the optimal course of action to maximize rewards for themselves in each state [6].
The research goals, open questions
Our goal is to model a single traffic intersection and find the best multipath plan for traffic flow by combining game theory and RL in a multi-agent system. By analyzing dynamic and simulated traffic data, it adaptively controls traffic flow at all stages, automatically managing the operation of traffic lights rather than adjusting the timing plans of the traffic light. Thus, to improve the traffic situation, we proposed a semi-cooperative Nash Q-learning that can learn about and evaluate the advantages and disadvantages of the change in the state of environment after the agents have taken the selected joint action. It updates Q-function based on Nash equilibrium of the current Q-values and selects Nash equilibrium solution with cooperative behaviour due to the informational non-uniqueness in the learning process. However, the distribution of traffic between traffic sections is generally unbalanced, which sometimes leads to inefficient controls. To fill this gap, we evaluate and examine the extended version - a semi-collaborative Stackelberg Q-learning that replaces the Stackelberg equilibrium solution with Nash equilibrium in updating the Q-function. More specifically, there are two hierarchical equilibrium solutions in Stackelberg equilibrium. The agent with the largest queues is the leader and the others are three followers, and the leader can dominate the highest priority in the decision-making process.
Methods
Model formulation
Fig.1 shows a common structure of an intersection with four inbound links
(i.e.,
![]() ...
...![]() )
where vehicles arrive from outside the queues and four outbound connections
(i.e.,
)
where vehicles arrive from outside the queues and four outbound connections
(i.e.,
![]() ...
...![]() )
through which the vehicles leave the intersection. In this case, the single
red and green states of the traffic light can be considered controllable,
which can be coded as follows: 0 and green: 1.
)
through which the vehicles leave the intersection. In this case, the single
red and green states of the traffic light can be considered controllable,
which can be coded as follows: 0 and green: 1.
Game theoretical framework
This system can be modelled as a non-cooperative non-zero sum game, inbound
traffic links are commonly treated as players, and the status of signal light
(green or red) is considered the decision.
Nash equilibrium
(called
prisoner’s dilemma
in the classic example) is usually feasible to achieve a rational balance for
all players. Each player strives for an outcome that provides him with the
lowest possible cost
![]() ,
and no player can better improve performance no matter how he/she changes the
decision
,
and no player can better improve performance no matter how he/she changes the
decision
![]() that
can be expressed in Eq. (1).
that
can be expressed in Eq. (1).
![]() (1)
(1)
Stackelberg equilibrium has hierarchical levels among players compared with Nash equilibrium. The leader imposes his strategy on the followers, and then the followers make the optimal joint decisions based on the decisions made by the leader.
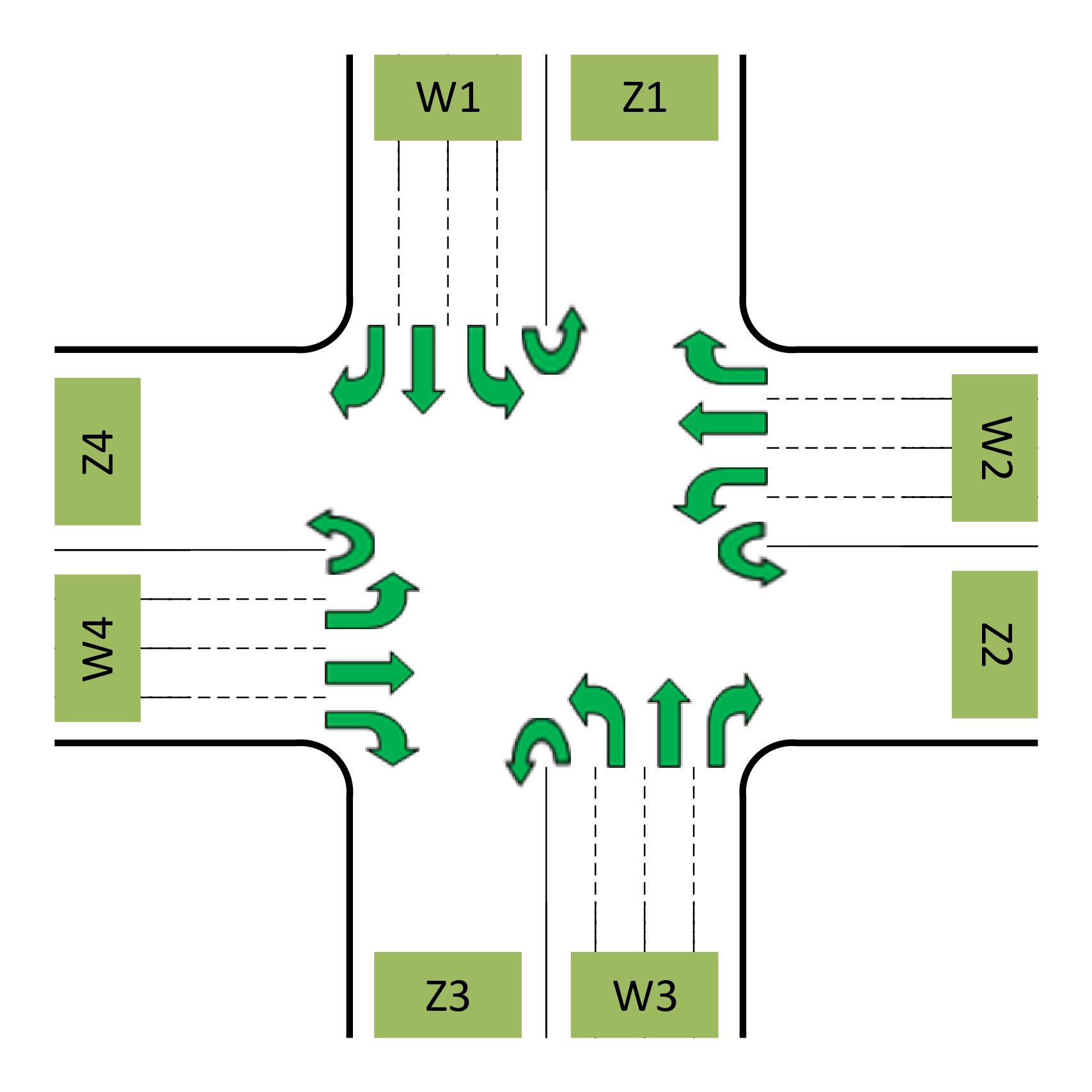
Fig. 1. General structure of the intersection
Q learning
In
RL, agents (players) learn a policy
![]() mapping
to an action
mapping
to an action
![]() (decision)
from the current state
(decision)
from the current state
![]() .
The Q-function evaluating the expected and discounted cumulative reward
.
The Q-function evaluating the expected and discounted cumulative reward
![]() can
be updated according to Eq. (2):
can
be updated according to Eq. (2):
![]() (2)
(2)
Where
![]() is
the learning rate, which determines the extent to which newly acquired
information overwrites old information. The discount factor
is
the learning rate, which determines the extent to which newly acquired
information overwrites old information. The discount factor
![]() determines
the importance of future rewards.
determines
the importance of future rewards.
Semi-cooperative Nash/Stackelberg Q-Learning
Semi-cooperative Nash/Stackelberg Q-learning is an algorithm that combines reinforcement learning and game theory in a multi-agent system, where the maximum operator is replaced by equilibrium solutions to update Q-values. Q-values are updated according to Eq. (3):
![]() (3)
(3)
Where
![]() is
the Q-value of the
is
the Q-value of the
![]() agent
when all agents jointly take actions
agent
when all agents jointly take actions
![]() in
state
in
state
![]() ,
and
,
and
![]() is
the Nash/Stackelberg solution. The multi-agent Q-function differs from the
single-agent Q-function in Eq. (2), in which the agent must consider not only
his own reward but also that of other agents to receive feedback on
equilibrium solutions.
is
the Nash/Stackelberg solution. The multi-agent Q-function differs from the
single-agent Q-function in Eq. (2), in which the agent must consider not only
his own reward but also that of other agents to receive feedback on
equilibrium solutions.
Results
In
the experiment, the setting parameters of semi-cooperative Nash/Stackelberg
Q-learning are examined, with a learning rate and discount factor of
![]() and
and
![]() ,
respectively. The constant strategy (i.e., the time intervals of green or red
lights are fixed and periodic) commonly used in reality, and the
semi-cooperative Nash/Stackelberg Q-learning methods are implemented and
compared.
,
respectively. The constant strategy (i.e., the time intervals of green or red
lights are fixed and periodic) commonly used in reality, and the
semi-cooperative Nash/Stackelberg Q-learning methods are implemented and
compared.
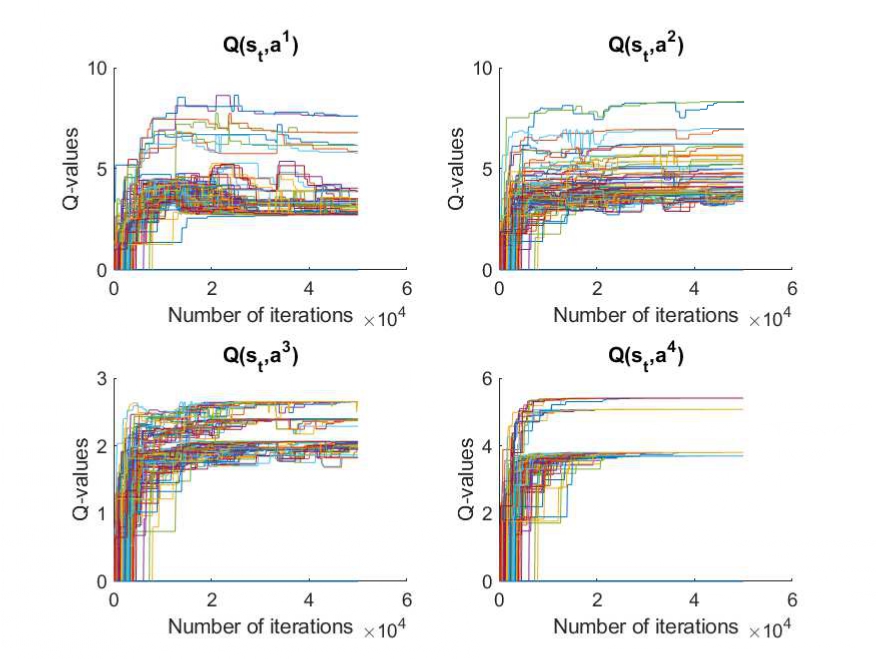
Fig. 2. Q-values of all agents with joint action that corresponds to the
current state
![]() in
semi-cooperative Nash Q-learning in one episode.
in
semi-cooperative Nash Q-learning in one episode.
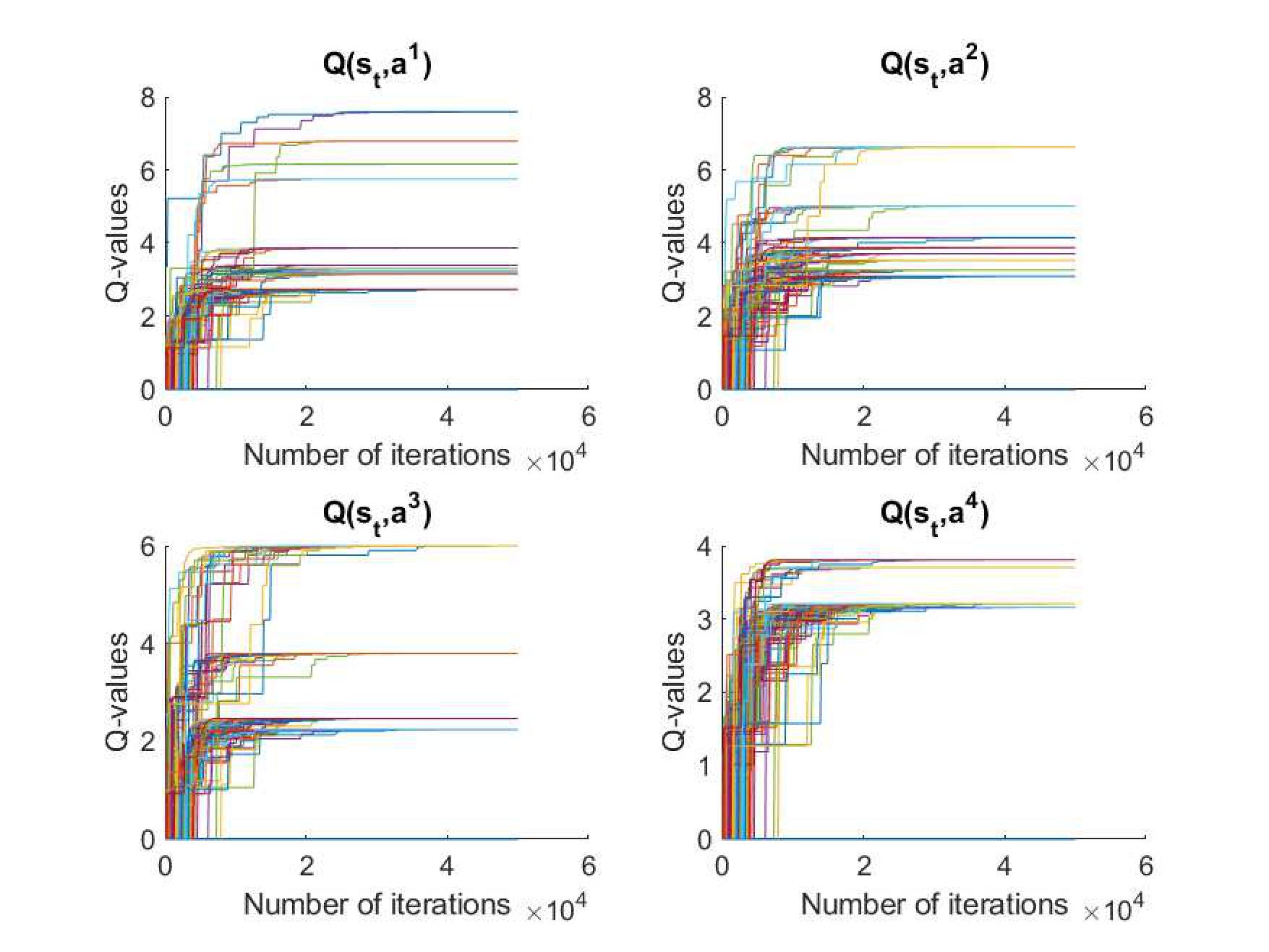
Fig. 3. Q-values of all agents with joint action that corresponds to the
current state
![]() in
semi-cooperative Stackelberg Q-learning in one episode.
in
semi-cooperative Stackelberg Q-learning in one episode.
Fig. 2 shows the Q-values of all the agents corresponding to the different
joint actions and current state, which are illustrated in one episode (i.e.,
50,000 iterations). In semi-cooperative Nash Q-learning, the subset for
![]() can
be considered as an example to be introduced with each curve representing the
Q-values of the agent taking the joint actions that are exploited and explored
based on Nash equilibrium. It can be observed that as the iterations increase,
all curves converge, and finally the optimal joint actions corresponding to
the Nash equilibrium are selected. Meanwhile, compared to Figure 3, the
Q-values of semi-cooperating Nash Q-learning show that they converge earlier
and more stably with the same number of iterations.
can
be considered as an example to be introduced with each curve representing the
Q-values of the agent taking the joint actions that are exploited and explored
based on Nash equilibrium. It can be observed that as the iterations increase,
all curves converge, and finally the optimal joint actions corresponding to
the Nash equilibrium are selected. Meanwhile, compared to Figure 3, the
Q-values of semi-cooperating Nash Q-learning show that they converge earlier
and more stably with the same number of iterations.
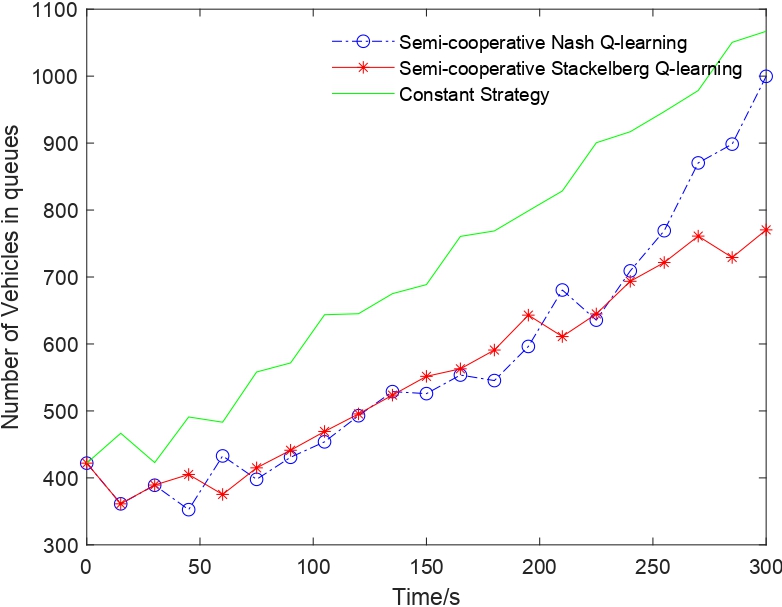
Fig. 4. Comparison of vehicles waiting at the traffic light "Queues" in 20 time slices (300 seconds)
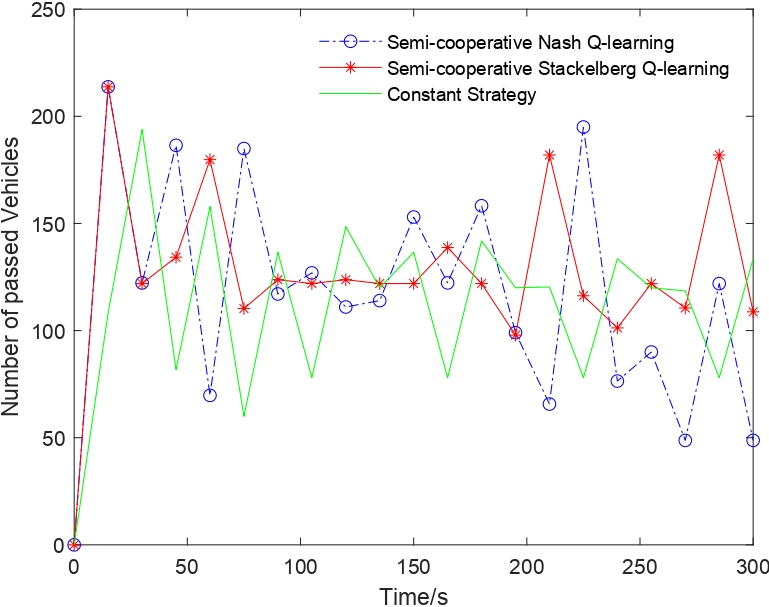
Fig. 5. Comparison of vehicles passing the intersection in 20 time slices (300 seconds)
Figs. 4, 5 show the changing trend of the vehicles waiting at the traffic light "Queues'' and vehicles passing through the intersection for semi-cooperative Nash/Stackelberg Q-learning and constant strategy. In Fig. 4, the queue length increases as time goes by due to the vehicles coming from outside the queues, and the number of passing vehicles tends to be periodic in Fig. 5. The sum of the vehicles passing through in total in 20 time slices for semi-cooperative Nash/Stackelberg Q-learning and constant strategy are 2425, 2655, 2343, respectively.
Expected impact and further research
These results were compared with the constant strategy, suggesting that the semi-collaborative Nash and Stackelberg Q-learning achieved improvements of approximately 3.50% and 13.32%, respectively, for queues and vehicles in transit. The semi-cooperative Stackelberg Q-learning algorithm may perform better than the semi-cooperative Nash Q-learning algorithm. These two algorithms are flexible and adaptive enough to be implemented in reality to control traffic lights while the communication information is limited between agents.
Future work will model a global network of intersections. Additionally, more conditions and constraints will be added to make the simulation more realistic.
Publications, references, links
List of corresponding own publications.
[S1] J. Guo, I. Harmati. Optimization of Traffic Signal Control Based on Game Theoretical Framework. Proceedings of the Workshop on the Advances of Information Technology, Jan. 24, 2019, Budapest, Hungary, pp. 105–110.
[S2] J. Guo, I. Harmati. Traffic Signal Control Based on Game Theoretical Framework, The 22nd International Conference on Process Control (PC19), IEEE, June 11-14, 2019, Strbske Pleso, Slovakia, pp. 286-291.
[S3] J. Guo, I. Harmati. Optimization of traffic signal control based on game theoretical framework, The 24th International Conference on Methods and Models in Automation and Robotics (MMAR), IEEE, August 26-29, 2019, Międzyzdroje, Poland, pp. 354–359.
[S4] J. Guo, I. Harmati. Optimization of traffic signal control with different game theoretical strategies, The 23rd International Conference on System Theory, Control and Computing (ICSTCC), IEEE, October 9-11, 2019, Sinaia, Romania, pp. 750–755.
[S5] J. Guo, I. Harmati. Reinforcement Learning for Traffic Signal Control in Decision Combination. Proceedings of the Workshop on the Advances of Information Technology, Jan. 30, 2020, Budapest, Hungary, pp. 13-20.
[S6] J. Guo, I. Harmati. Comparison of Game Theoretical Strategy and Reinforcement Learning in Traffic Light Control. Journal of Periodica Polytechnica Transportation Engineering, 2020, 48 (4), pp.313-319.
[S7] J. Guo, I. Harmati. Evaluating multiagent Q-learning between Nash and Stackelberg equilibrium for traffic routes plan in a single intersection, Control Engineering Practice, 2020, 102, p. 104525.
[S8] H. He, J. Guo, K. Molnar. Triboelectric respiration monitoring sensor and a face mask comprising such as a triboelectric respiration monitoring sensor. Patent application, Filed, 2021, Hungary, P2100102.
[S9] J. Guo, I. Harmati. Traffic lane-changing modeling and scheduling with game theoretical strategy, The 25th International Conference on Methods and Models in Automation and Robotics (MMAR), IEEE, August 23-26, 2021, Międzyzdroje, Poland, pp. 197-202.
[S10] S. Taik, J. Guo, B. Kiss, and I. Harmati. Demand Response of Multiple Households with Coordinated Distributed Energy Resources, The 25th International Conference on Methods and Models in Automation and Robotics (MMAR), IEEE, August 23-26, 2021, Międzyzdroje, Poland, pp. 203-208.
[S11] H. He, J. Guo, B. Illés, A. Géczy, B. Istók, V. Hliva, D. Török, J.G. Kovács, I. Harmati and K. Molnár. Monitoring multi-respiratory indices via a smart nanofibrous mask filter based on a triboelectric nanogenerator, Nano Energy, 2021, 89, p. 106418.
[S12] J. Guo, I. Harmati. Lane-changing decision modelling in congested traffic with a game theory-based decomposition algorithm, Engineering Applications of Artificial Intelligence, 2022, 107, p. 104530.
Table of links.
- https://en.wikipedia.org/wiki/Nash_equilibrium
- https://en.wikipedia.org/wiki/Prisoner%27s_dilemma
- https://en.wikipedia.org/wiki/Stackelberg_competition
List of references.
[1] Chiu S. Adaptive traffic signal control using fuzzy logic. In Proceedings of the Intelligent Vehicles92 Symposium 1992 Jun 29 (pp. 98–107). IEEE.
[2] Wang Y, Yang X, Liang H, Liu Y. A review of the self-adaptive traffic signal control system based on future traffic environment. Journal of Advanced Transportation. 2018 Jun 27;2018.
[3] Guo J, Harmati I. Optimization of Traffic Signal Control with Different Game Theoretical Strategies. In2019 23rd International Conference on System Theory, Control and Computing (ICSTCC) 2019 Oct 9 (pp. 750–755). IEEE.
[4] Sutton RS, Barto AG. Introduction to reinforcement learning. Cambridge: MIT press; 1998 Mar1.
[5] Abdulhai B, Pringle R, Karakoulas GJ. Reinforcement learning for true adaptive traffic signal control. Journal of Transportation Engineering. 2003 May;129(3):278–85.
[6] Junchen J, Xiaoliang M. A learning-based adaptive signal control system with function approximation. IFAC-PapersOnLine. 2016 Jan 1;49(3):5–10.
