|
|
BMe Research Grant |
|
Pattantyús-Ábrahám Doctoral School of Mechanical Engineering
BME Gépészmérnöki Kar, Department of Applied Mechanics
Supervisor: Dr. Insperger Tamás
Modelling of human balancing on rolling balance board in the frontal plane
Introducing the research area
Nowadays, the number of falls caused by imbalance is increasing, especially among the elderly. In particular, decreasing certainty of perception, the inactive lifestyle, weakness of the muscles and the increasing reaction time increase the risk of falls[1]. Theoretical and experimental investigation of simple balancing tasks helps understand the control concept of the central nervous system (CNS), therefore, the potential falls can be predicted and prevented.
Brief introduction of the research place
The research was carried out at the Department of Applied Mechanics and MTA-BME Lendület Human Balancing Research Group, supervised by Tamás Insperger. The goal of the research group is to understand and find a simple control model of the operation of the CNS. Low degree-of-freedom mechanical models of different balancing tasks are investigated, and devices are designed to improve the balancing ability.
History and context of the research
The most common activities in everyday life, such as standing, sitting, or walking are performed about unstable equilibria. The CNS, among others, plays an important role in the stabilization of the human body. The visual, vestibular, and somatosensory organs obtain information about the position and velocity of the human body. The CNS determines the necessary interaction to maintain balance based on the measured signals, which results in a corrective movement. Delivering and processing the information takes some time, therefore, the so-called reaction time delay is involved in the process. The operation of the CNS is often modeled as a delayed proportional-derivative (PD) feedback, where the delay corresponds to the human reaction time [2–4].
The balancing performance is limited by the so-called critical feedback delay. If the loop delay is larger than the critical value, the equilibrium cannot be stabilized. For stick balancing on fingertip, the critical delay is affected by the length of the stick, if the control force is modelled as delayed PD feedback. The critical delay is 200 ms for a 30 cm long stick. If the reaction time of the balancing subject is larger than 200 ms, then the stick cannot be stabilized.
In case of still standing, the critical delay is four times the human reaction time due to the passive stiffness at the ankle joints. Thus, a rolling balance board is used to reduce the critical delay (Fig. 1).

Figure 1 Rolling balance board of adjustable wheel radius.
The research goals, open questions
The focus of the present study is on the difficulty of the balancing task, with special attention to the effect of wheel radius of the balance board and stance width. Balancing experiments on young healthy adults were analyzed in the frontal plane, i.e., plane of tilting to the side (Fig. 2c). Reflective markers were placed on the human body segments and the balance board, to be recordable by OptiTrack motion capture system.
A two- and three-degree-of-freedom mechanical models of balancing on balance board in the frontal plane were constructed (Fig. 2a-b). The rolling balance board corresponds to a single degree-of-freedom (DoF). In the 2-DoF model, the second DoF is related to the four-bar linkage mechanism modelling the human body. The relative movement of the upper body and the lower limbs is taken into account in the 3-DoF model; therefore, the human body has 2-DoFs. The biomechanical literature refers to one- and two-degree-of-freedom human body models as ankle and ankle-hip strategies, respectively [5].
The following three hypotheses were set up.
H1. It is more difficult to balance with wheel radius–stance width combinations associated with smaller critical delay.
H2. The reaction time can be estimated indirectly based on the critical time delays obtained from the model and successful-unsuccessful balancing trials with different wheel radius-stance widths.
H3. Applying ankle–hip strategy is more efficient than ankle strategy in the sense that the critical delays associated with ankle–hip strategy (3-DoF model) are larger.

Figure 2 a) Two degree-of-freedom mechanical model of balancing on rolling balance board in the frontal plane. b) Three degree-of-freedom mechanical model of balancing on rolling balance board in the frontal plane. c) Balancing on rolling balance board in the frontal plane. d) Measuring the response time to visual input.
Methods
Ten young healthy adults participated in the experiment. First, the response time of the participant was assessed for visual input (randomly timed light flash). In response, the subject had to push a pedal as fast as possible (Fig. 2d). Second, the subject was asked to balance for 30 s on balance boards of six selected wheel radii (20, 15, 12.5, 10, 7.5 and 5 cm) and in three stance widths (40, 25 and 15 cm) with stretched legs, open eyes, and arms behind the back.
The joints between the rigid bodies in the mechanical model correspond to the
ankle, hip, and lumbar joints. The intrinsic stiffness at the ankle joints and
the lumbar region was described by torsional springs of constant stiffness.
The human body related parameters were calculated based on the corresponding
literature [6–9]. The control torque acts at the hip in both models. The
operation of the CNS is modelled as a delayed PD feedback; therefore, the
equation of the control torque involves four control gains for the 2-DoF and
six for the 3-DoF model. For the sake of simplicity, the sensory organs are
not distinguished by their different feedback delays, and a so-called
equivalent, constant
![]() delay
is included in the control loop.
delay
is included in the control loop.
The linearized governing equations are a set of delay differential equations. The upper equilibrium is stable if all the characteristic exponents have negative real parts. For a fixed human and balance board data set, the stability is determined by the control gains and the delay. For a fixed delay, there exists a 4- or 6-dimensional domain of the stabilizing control gains. The size of the domain typically shrinks as the delay increases and completely disappears at the so-called critical time delay.
The critical delay is related to the balancing ability. If the reaction time is greater than the critical delay associated with a certain configuration, the subject is unable to balance with that configuration according to the model. The critical delays were determined based on an analytical method [10–11]. The result, the so-called stabilizability diagrams can be seen in Fig. 3 on a gray scale.
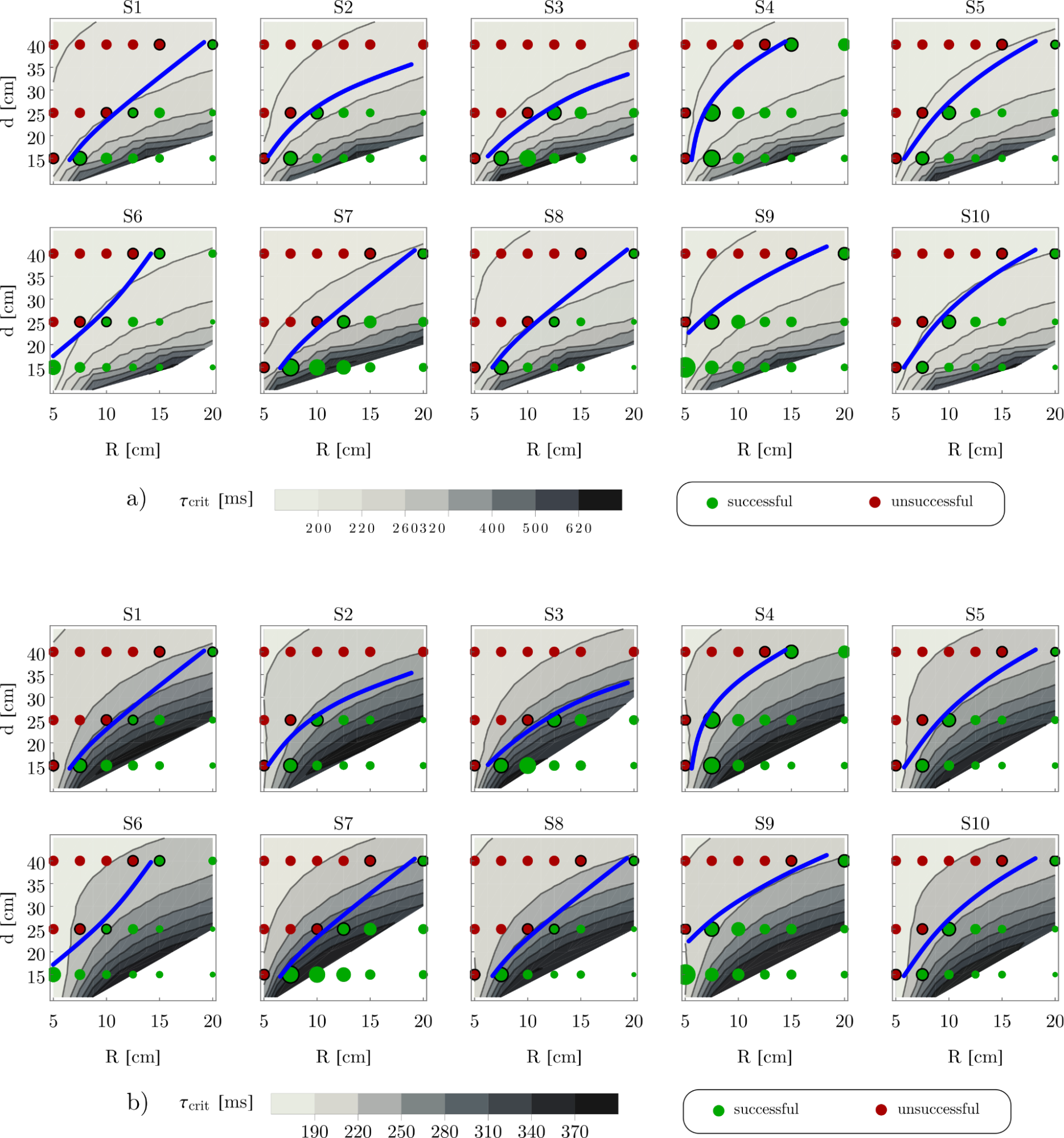
Figure 3 a) Stabilizability diagrams for the two degree-of-freedom mechanical model. b) Stabilizability diagrams for the three degree-of-freedom mechanical model.
Results
In Fig. 3, the successful and unsuccessful balancing trials of the subjects are shown with green and red markers, respectively. The task gets more challenging with increasing stance width and decreasing wheel radius. Reaction time is estimated as the average of the critical delays associated with adjacent markers (indicated by the black edge) on the blue separating line. The estimated reaction times based on the 2-DoF model are shown in blue and those based on the 3-DoF model in red in Fig. 4. Black markers indicate the measured response times. For all subjects , the measured response time is greater than the estimated reaction time based on the models. This can be explained by the fact that the response time is the sum of the reaction time (the time between the flash and the muscle contraction) and the movement time of the foot. However, the reaction time can be estimated from the stabilizability diagram.
The estimated reaction times are in the range of 198–239 ms (average: 214 ms) for the 2-DoF and 201–282 ms (average: 228 ms) for the 3-DoF model, slightly longer than the literature data for standing still (90–125 ms) [12–15]. This is because balancing on the balance board requires processing of more complex signals, which can take longer.
Hypothesis H1 was accepted. The area of the green and red markers is proportional to the standard deviation of the angle of the balance board during the actual trial in Fig. 3. The standard deviation can be considered as a measure of the difficulty of the balancing task: the larger the standard deviation, the more difficult the task. Stabilizability diagrams show that the standard deviation typically increases with decreasing critical time delay. Further decrease leads to unsuccessful trials confirming hypothesis H1.
Hypothesis H2 was also accepted. On the one hand, the blue line separating the successful and unsuccessful trials fits into the structure of the contour lines of the stabilizability diagram. On the other hand, the strong correlation between the estimated response time based on the models and on the measured response time (correlation coefficients of 0.77 and 0.78, respectively) suggests that the response time can be estimated indirectly based on the stabilization diagram and experiments.
Hypothesis H3 can be accepted for difficult tasks. For easy tasks (large wheel radius, small stance width), the critical delays of the 2-DoF model are greater than those of the 3-DoF model. However, for difficult tasks (small wheel radius, large stance width), the critical time delays are indeed greater for the 3-DoF model, which verifies the ankle–hip strategy.
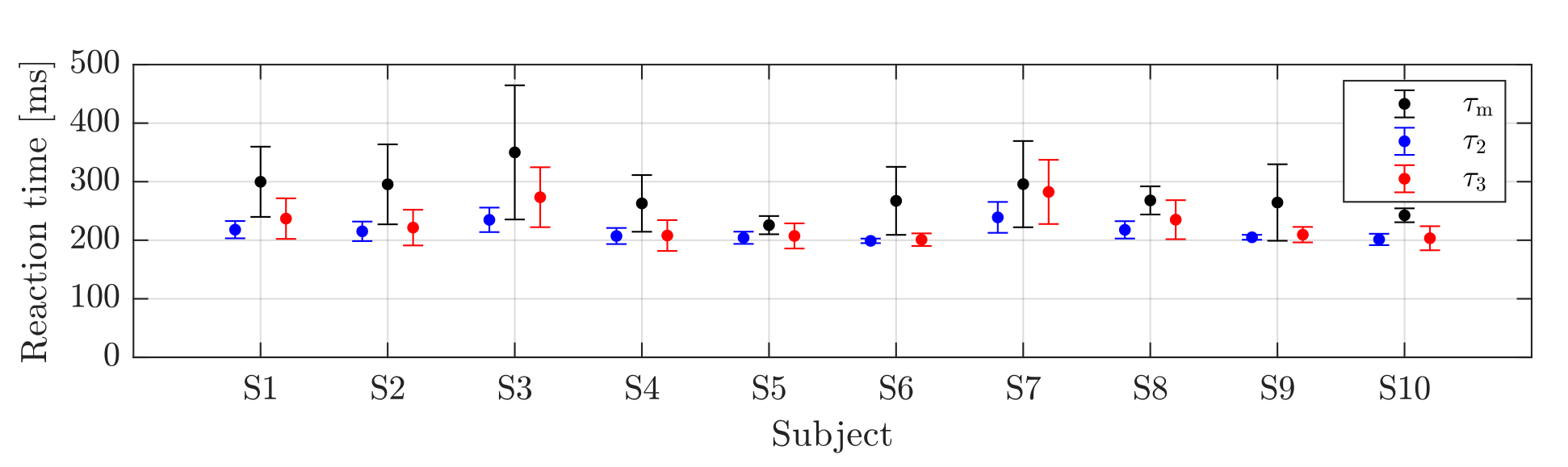
Figure. 4 Estimated reaction times based on the mechanical models and the measured response times.
Expected impact and further research
The presented results will be submitted to a highly ranked international journal. The model involves the most frequent causes of accidents: reaction time, and physical properties of muscles which later can be completed with the sensory uncertainty. In the future, measurements will be performed involving subjects with balance disorders and a strategy will be developed to identify the factor causing the imbalance based on the stabilizability diagram and experiments. The balance board is suitable for monitoring the balancing ability due to its variable, well-defined parameters. Our goal is to develop a series of exercises that can contribute to the improvement of balancing ability and intensive rehabilitation after the accidents.
Publications, references, links
List of corresponding own publications.
S1. Molnar CA, Zelei A, Insperger T. Rolling balance board of adjustable geometry as a tool to assess balancing skill and to estimate reaction time delay. Journal of the Royal Society Interface 2021; 18(176):20200956. (IF=3.748)
S2. Molnar CA, Balogh T, Boussaada I, Insperger T. Calculation of the critical delay for the double inverted pendulum. Journal of Vibration and Control 2021; 27(3-4):356–64. (IF=2.169)
S3. Molnar CA, Insperger T. Parametric study of changes in human balancing skill by repeated balancing trials on rolling balance board. Periodica Polytechnica Mechanical Engineering 2020; 64(4):317–27.
S4. Wang Z, Liang S, Molnar CA, Insperger T, Stepan G. Parametric continuation algorithm for time-delay systems and bifurcation caused by multiple characteristic roots. Nonlinear Dynamics 2021; 103(4):3241–53. (IF=4.867)
S5. Molnar CA, Insperger T. Estimation of reaction time during human balancing on rolling balance board based on mechanical models. in: International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 2020; 83914:V002T02A033, online.
S6. Molnar CA, Insperger T. Egyensúlyozási képességek fejlődésének vizsgálata egyensúlyozó deszkán. in: XIII. Magyar Mechanikai Konferencia 2019; p 4, Miskolc, Hungary.
S7. Molnar CA, Varszegi B, Insperger T. Identification of sensory dead zones in human balancing on balance board. in: Proceedings of the European Control Conference (ECC) 2019; 2904–2909., Naples, Italy.
S8. Molnar CA, Zelei A, Insperger T. Human balancing on rolling balance board in the frontal plane. in: IFAC-PapersOnLine 2018; 51(14):300–305., Budapest, Hungary.
S9. Molnar CA, Zelei A, Insperger T. Mechanical model for human balancing on rolling balance board. Acta Polytechnica CTU Proceedings 2018; 18:32–37.
S10. Zelei A, Molnar CA, Insperger T. Four-bar mechanism substitution for balance board experiments: A parametric study. in: Proceeding of the Dynamical Systems in Applications 2018; 473–484., Lodz, Poland.
S11. Molnar CA, Zelei A, Insperger T. Egyensúlyozó deszkán való egyensúlyozási képességek modellezése a sagittalis síkban. in: OGÉT 2017: 25th International Conference on Mechanical Engineering 2017; 283–286. Cluj-Napoca, Romania.
Table of links.
Department of Applied Mechanics
MTA-BME Lendület Human Balancing Research Group
List of references.
[1] Robinovitch SN, Feldman F, Yang Y, Schonnop R, Leung PM, Sarraf T, Sims-Gould J, Loughin M. Video capture of the circumstances of falls in elderly people residing in long-term care: an observational study. The Lancet 2013; 381(9860):47–54.
[2] Mehta B, Schaal S. Forward models in visuomotor control. Journal of Neurophysiology 2002; 88(2):942–53.
[3] Maurer C, Peterka JP. A new interpretation of spontaneous sway measures based on simple model of human postural control. Journal of Neurophysiology 2005; 93:189–200.
[4] Stepan G. Delay effects in the human sensory system during balancing. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2009; 367(1891):1195–212.
[5] Runge CF, Shupert CL, Horak FB, Zajac FE. Ankle and hip postural strategies defined by joint torques. Gait & Posture.1999; 10(2):161–70.
[6] Trevino J, Lee H. Sex differences in 2-DOF human ankle stiffness in relaxed and contracted muscles. Annals of Biomedical Engineering 2018; 46(12):2048–56.
[7] Nalam V, Adjei E, Lee H. Quantification and Modeling of Ankle Stiffness During Standing Balance. IEEE Transactions on Biomedical Engineering 2020; 68(6):1828–37.
[8] McGill S, Seguin J, Bennett G. Passive stiffness of the lumbar torso in flexion, extension, lateral bending, and axial rotation. Effect of belt wearing and breath holding. Spine 1994; 19(6):696–704.
[9] De Leva P. Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters. Journal of Biomechanics 1996; 29(9):1223–30.
[10] Molnar CA, Balogh T, Boussaada I, Insperger T. Calculation of the critical delay for the double inverted pendulum. Journal of Vibration and Control 2021; 27(3–4):356–64.
[11] Boussaada I, Niculescu SI. On the dominancy of multiple spectral values for time-delay systems with applications. IFAC-PapersOnLine 2018; 51(14):55–60.
[12] Kiemel T, Oie KS, Jeka JJ. Slow dynamics of postural sway are in the feedback loop. Journal of Neurophysiology 2006; 95(3):1410–8.
[13] Li Y, Levine WS, Loeb GE. A two-joint human posture control model with realistic neural delays. IEEE Transactions on Neural Systems and Rehabilitation Engineering 2012; 20(5):738–48.
[14] Pasma JH, Boonstra TA, van Kordelaar J, Spyropoulou VV, Schouten AC. A sensitivity analysis of an inverted pendulum balance control model. Frontiers in Computational Neuroscience 2017; 11:99.
[15] Milton J, Insperger T. Acting together, destabilizing influences can stabilize human balance. Philosophical Transactions of the Royal Society A 2019; 377(2153):20180126.
