|
|
BMe Research Grant |
|
Kandó Kálmán Doctoral School of Transportation and Vehicle Engineering
BME KJK, Department of Automotive Technologies
Supervisor: Dr. Török Árpád
Optimizing highly automated systems’ transport processes
Introducing the research area
The rapid development of vehicle technology implies the change of future transport systems. The expected increase in the number of autonomous vehicles creates the opportunity to influence the system more efficiently. As a result, losses related to the transport processes can be reduced, traffic is expected to become safer, and severe research fields open up. My work aimed to characterize and improve the flow and safety of traffic in an environment used only by autonomous vehicles. I have developed a time-and-space-discrete, binary integer optimization model to combine the goals and tools of cooperative vehicle control and dynamic traffic management. The indicators characterizing road safety and the effects of mapping structures of the environment have been determined with the help of the elaborated model.
Brief introduction of the research place
My research work is carried out at the Department of Automotive Technologies of BME, in the Automotive Safety and Security research group led by Dr. Árpád Török. The purpose of the group is the integrated mathematical modeling of security and cyber security aspects related to vehicle development processes to minimize the security risks associated with highly automated vehicle systems. The department closely cooperates with the leading industrial stakeholders and research centers in the field.
History and context of the research
The growing number of highly automated vehicles on our roads will make it possible to control the transport system more efficiently [1], [2]. However, the large number of system components significantly increases the related optimization problems' complexity [3]. Moreover, it is not self-evident what governing principles and components the future transport management will be built on [4], [5]. Some research focuses on solving individual vehicle decision problems [6], while others focus on developing network-level solutions. In the latter case, the position and movements of the vehicles are assumed to be influenced by a central management system supporting the approach of the system level optimum [7].
Safety requirements of autonomous transport systems have been regarded significant [8], [9]. Whatever direction the future transport system takes, the elementary parts of the space and infrastructure used for vehicle maneuvers must be unambiguously assigned to the vehicles. This requirement is met by the occupancy-grid concept (Fig. 1) used for the navigation of autonomous transport systems [10].
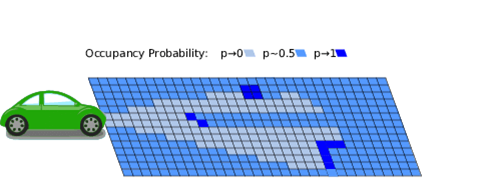
Figure 1: Representation of the occupancy-grid concept [11]
However, based on the literature review, the representation of the transport environment modeling the spatial structure is mainly considered as a defined factor rather than an active element of the transport system. The occupancy-grid concept was investigated by many research studies [12], [13], but these were not primarily aimed at examining the correlation of grid structure and efficiency. Beyond this, it can also be stated that the structures of the surrounding world’s spatial representation in automated vehicle management systems are generally based on a square grid structure, although it is clear that different structures can also be used.
The research goals, open questions
Considering the reviewed works and the significant potentials regarding the automatization of the vehicles, my research focused on a totally autonomous passenger transport system. Thus, the movements and decisions of the individual vehicles were considered to be centrally influential. To maximize the efficiency of the transport system, my aim was to develop a traffic management procedure that ensures the system-level minimization of losses (e.g., travel time, accident risk) related to the transport process. In the light of the growing expectations for road safety, my further goal was to develop and examine the safety parameters characterizing the operation of the autonomous transport system.
To achieve the research goals, the development of a framework suitable for traffic demand management of the autonomous transport system was needed in the first step. It was necessary to examine the methods by which the traffic distribution problem can be solved efficiently, even in real-time. It was also a fundamental research aim to examine the possibilities of extending the basic model to consider the effects of external parameters (e.g., road toll structure) on the travel demands, designed traffic flows, and efficiency.
By discretizing the transport network and the considered timeframe, my goal was to improve the basic model, creating a framework that can determine the movements and decisions of the individual vehicles rather than traffic flows. This system can optimize transport processes by combining the tools and aims of cooperative vehicle control and real-time traffic management. For validation purposes, implementation of the dynamic model in MATLAB software and testing on different sample road networks were required. To realize real-time traffic optimization, the complexity of the equation and inequality systems describing the model had to be kept to a minimum.
The elaborated dynamic model ensured the opportunity to investigate the efficiency and traffic safety of the autonomous transport system. Besides the investigation of the optimization objective function, this required the development of different safety indicators. In addition, the effects of the representation of the transport environment by different grid structures were also revealed.
Methods
During the development of the time and space discretized dynamic model, a binary integer variable was formed to simplify the optimization and support the real-time operation (Fig. 2). The decision variable (xk,j,i) of the model describes the presence of vehicle k in location i at the time step j, with a binary set of values.
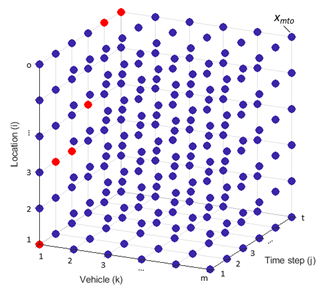
Figure 2: Structure of the 3D array containing the optimized variables
(the trajectory of the first vehicle is highlighted in red)
Given that computers cannot handle an infinite number of continuous quantities, numerical models necessarily approach reality and its mathematical model with a finite number of variables. The process of transforming the continuous attributes into a finite number of categorical attributes is called discretization. To perform traffic management tasks, it became necessary to partition both the transport network (Fig. 3) and the time:
● the continuous-time domain was divided into integer time moments with a resolution of seconds,
● the transport network was divided into directed polygons (locations) characterized by a 5-meter diameter inscribed circle (considering the dimension of an average passenger car).
Based on my observations, the applied resolution supports efficient traffic management by providing a high degree of detail while preserving a manageable degree of complexity.
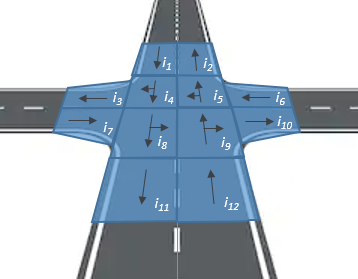
Figure 3: Structure of a simple intersection partitioned into locations
The further reduction of computational complexity was identified as an important task to support the real-time operation of the model while handling as many variables as possible. To achieve this goal, I have developed methods to reduce the number of constraining equations and inequalities without threatening the efficiency and reliability of the solution. The basic principle of the methods was to reduce the set of values of the variable taken into account in the terms describing the constraints:
● considering the speed limit, the location pairs that could not be traveled in one time step even at maximum speed were excluded from the further investigations,
● based on the maximum allowed value of acceleration, the range of locations available in the first time step was narrowed,
● the non-safety critical conditions were reduced by excluding the origin and destination locations (the special points of the network) from the investigation.
The results of traffic safety research formed the basis of the methodological development of the indicators characterizing the safety of the transport system. To investigate the risk of safety-critical system conditions (collisions), my aim was to determine the number and temporal distance of crossing vehicle movements. Recognizing also that the safety of the transport system is greatly influenced by the speed characteristics of the vehicles [14], [15], [16], indicators characterizing their average values and homogeneity were also developed.
Results
Development of the base model
I developed an optimization model using the linear representation of the traffic distribution problem. The basic model can implement travel demands while minimizing the load of the transport network. To influence the demands at the strategic level, I integrated the road toll structure into the model by assigning costs to the routes of the network. Operation of the basic model was validated on example networks, and a sensitivity analysis was also performed, thus substantiating my further research work.
Improvement of the model
Improving the basic model by discretizing the transport network and time, I developed a vehicle-level control model of the autonomous transport system suitable for the implementation of network-level optimization tasks. During the development, micro (vehicle dynamics constraints) and macro (traffic flow optimization) level factors were also considered. The conditions of safe traffic management (e.g., collision avoidance, lane keeping, speed limit) were defined. I implemented the mathematical expressions describing the model in the MATLAB software and evaluated the operation and results on example networks representing diverse types of road intersections and multi-lane road sections.
Reducing the runtime of the simulation model
The detailed resolution of space and time causes a significant increase in computational complexity during the optimization. The increase of the resolution reduces the problem, but at the same time, reduces the efficiency of the optimization. Therefore, to reduce the runtime of the model, I developed procedures to reduce the number of constraining expressions. Furthermore, the established procedures can be used to exclude unnecessary and redundant checks and locations that are certainly not relevant in the case of the investigated trip (e.g., cannot be reached based on the speed limit). The individual and combined effects of the developed methods were evaluated with particular attention to the efficiency and reliability of the solution. Based on the findings, the procedures reduce computational complexity of up to 84-96%.
Development of safety indicators for autonomous transport systems
The presented model created the basis for traffic safety analyzes in autonomous transport systems. For this purpose, I developed indicators evaluating the safety of traffic flow. The safety indicators examine the number and temporal distance of crossing vehicle movements, as well as the values and homogeneity of vehicle speeds at the individual or network-level. On the one hand, the indicators can be used for the safety assessment and ranking of the traffic distribution solutions determined by the optimization. On the other hand, they provide the opportunity to examine the safety effects of different transport network structures or interventions applied to them.
Impact assessment of the structure of transport network representation
In addition to the traditionally used square-grids, the transport network can be represented by several other structures (e.g., using other regular polygons, as illustrated in Fig. 4). Using the developed model, I determined the effects of different network structures (e.g., hexagon-based, triangle-based representations) on traffic efficiency, computational complexity, and safety.
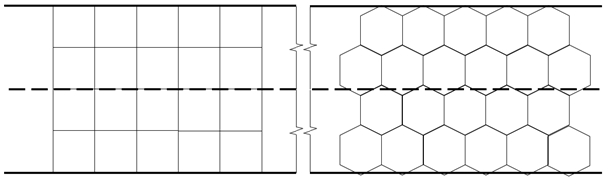
Figure 4: An example for the representation of a simple road section by different structures
The different structures were generated by aligning a set of new polygons around the base polygon. Comparability was ensured using polygons characterized by an inscribed circle of the same radius. For the calculations, I determined the number of locations and their connections, the covered area, and the computational complexity as a function of the grid generation steps. My results indicate that the square-grid representation of the road network may, in many respects, lag behind the characteristics of different structures created with the use of other polygons.
Expected impact and further research
The results of the research have significant potential for real-time, safety-focused, and efficient management of traffic in highly automated transport systems. The basic and the improved dynamic models have been published in highly quoted international journals, indicating the importance of the research topic. The developed methods for reducing the runtime of the model and characterizing the safety of the system, as well as the publication about the effects of network representation structures are under review at Q1 journals.
My further research is focused on the automated implementation of network representation and the extension of the currently 2D procedure to a 3D environment. Thereby, the methodology could provide an effective solution in other areas beyond transport (e.g., in the management of complex UAV systems).
Publications, references, links
List of corresponding own publications:
[S1] Pauer, G., Török, Á. (2019). Comparing System Optimum Based and User Decision Based Traffic Models in an Autonomous Transport System. Promet - Traffic & Transportation, 31(5), 581-589. DOI: https://doi.org/10.7307/ptt.v31i5.3151 (IF: 0.664)
[S2] Pauer, G., Török, Á. (2020). Binary integer modeling of the traffic flow optimization problem, in the case of an autonomous transportation system. Operations Research Letters, 49(1), 136-143. https://doi.org/10.1016/j.orl.2020.12.004 (IF: 0.757)
[S3] Pauer, G., Sipos, T., Török, Á. (2019). Statistical Analysis of the Effects of Disruptive Factors of Driving in Simulated Environment. Transport, 34(1), 1–8. DOI: https://doi.org/10.3846/transport.2019.6724 (IF: 1.053)
[S4] Pauer, G., Török, Á. (2022). Introducing a novel safety assessment method through the example of a reduced complexity binary integer autonomous transport model. Reliability Engineering & System Safety, 217, 108062. https://doi.org/10.1016/j.ress.2021.108062 (IF: 6,188)
[S5] Pauer, G., Török, Á. (2021 – submitted, under consideration). The impact of grid structures on decision support processes in future transport systems. Decision Support Systems (IF: 4.721)
[S6] Pauer, G., Török, Á. (2019). Static System Optimum of Linear Traffic Distribution Problem Assuming an Intelligent and Autonomous Transportation System. Periodica Polytechnica Transportation Engineering, 47(1), 64–67. DOI: https://doi.org/10.3311/PPtr.11548
[S7] Török, Á., Pauer, G. (2018). Optimization of Linear Traffic Distribution Problem in terms of the Road Toll Structure Assuming an Autonomous Transportation System. International Journal for Traffic and Transport Engineering, 8(1), 112–124. DOI: 10.7708/ijtte.2018.8(1).08
[S8] Török, Á., Pauer, G. (2017). Assessment of the Current Status of Intelligent Transport Systems Serving the Improvement of Road Safety in Hungary. Periodica Polytechnica Transportation Engineering, 45(2), 19–24. DOI: 10.3311/PPtr.9279
[S9] Pauer, G. (2017). Development Potentials and Strategic Objectives of Intelligent Transport Systems Improving Road Safety. Transport and Telecommunication, 18(1), 15-24. DOI: https://doi.org/10.1515/ttj-2017-0002
[S10] Pauer, G., Berta, T., Török, Á. (2017). Analysing the Impact of Road Safety Information System on Traffic Safety. Transbaltica 2017: Transportation Science and Technology, Procedia Engineering, Volume 187, 712-721. Vilnius, Lithuania. DOI: https://doi.org/10.1016/j.proeng.2017.04.445
[S11] Pauer, G. (2017). Defining the Optimization Process of Traffic Distribution Problem with Linear Programming Approach in case of Autonomous Transportation System. In MOSATT 2017 Modern Safety Technologies in Transportation: Proceedings of the International Scientific Conference, 124-130. Herlány, Slovakia. ISBN 978-80-553-2864-5.
[S12] Török, Á., Pauer, G. (2016). Intelligens közlekedési rendszerek közlekedésbiztonsági rangsorolása. Statisztikai Szemle, 94(4), 418-434. DOI: 10.20311/stat2016.04.hu0418
[S13] Pauer, G., Török, Á. (2019). Forgalomoptimalizáció különböző felépítésű hálózatokon autonóm közlekedési rendszerben. IX. Közlekedéstudományi Konferencia, Győr, Hungary.
Table of links:
https://auto.bme.hu/kutatas/#biztonsag-es-vedelem
List of references:
[1] Tettamanti, T., Varga, I., Szalay, Z. (2016). Impacts of autonomous cars from a traffic engineering perspective. Periodica Polytechnica Transportation Engineering, 44(4), 244–250. https://doi.org/10.3311/PPtr.9464
[2] Speranza, M.G. (2018). Trends in transportation and logistics. European Journal of Operational Research, 264(3), 830-836. https://doi.org/10.1016/j.ejor.2016.08.032
[3] Zöldy, M. (2018). Investigation of autonomous vehicles fit into traditional type approval process. Proceedings of ICTTE, Belgrade, Serbia, 428–432.
[4] Levin, M.W., Odell, M., Samarasena, S., Schwartz, A. (2019). A linear program for optimal integration of shared autonomous vehicles with public transit. Transportation Research Part C: Emerging Technologies, 109, 267–288. https://doi.org/10.1016/j.trc.2019.10.007
[5] Cokyasar, T., Larson, J. (2020). Optimal assignment for the single-household shared autonomous vehicle problem. Transportation Research Part B: Methodological, 141, 98–115. https://doi.org/10.1016/j.trb.2020.09.003
[6] Van Brummelen, J., O’Brien, M., Gruyer, D., Najjaran, H. (2018). Autonomous vehicle perception: The technology of today and tomorrow. Transportation research part C: emerging technologies, 89, 384–406. https://doi.org/10.1016/j.trc.2018.02.012
[7] Javed, M.A., Zeadally, S., Hamida, E.B. (2019). Data analytics for cooperative intelligent transport systems. Vehicular communications, 15, 63–72. https://doi.org/10.1016/j.vehcom.2018.10.004
[8] Jacobstein, N. (2019). Autonomous vehicles: An imperfect path to saving millions of lives. Science robotics, 4(28), eaaw8703. DOI: 10.1126/scirobotics.aaw8703
[9] Li, L., Wang, X., Wang, K., Lin, Y., Xin, J., Chen, L., Wang, F.Y. (2019). Parallel testing of vehicle intelligence via virtual-real interaction. Science robotics, 4(28), eaaw4106. DOI: 10.1126/scirobotics.aaw4106
[10] Elfes, A. (1989). Occupancy grids: A probabilistic framework for robot perception and navigation. Ph.D. Thesis, Carnegie-Mellon University, Pittsburgh, PA.
[11] Rakotovao, T., Mottin, J., Puschini, D., Laugier, C. (2015). Real-Time Power-Efficient Integration of Multi-Sensor Occupancy Grid on Many-Core. Proceedings of the 2015 IEEE International Workshop on Advanced Robotics and its Social Impacts (ARSO), Lyon, France, 1-6. DOI: 10.1109/ARSO.2015.7428211
[12] Daudelin, J., Jing, G., Tosun, T., Yim, M., Kress-Gazit, H., Campbell, M. (2018). An integrated system for perception-driven autonomy with modular robots. Science robotics, 3(23), eaat4983. DOI: 10.1126/scirobotics.aat4983
[13] Ramakrishnan, S.K., Jayaraman, D., Grauman, K. (2019). Emergence of exploratory look-around behaviors through active observation completion. Science robotics, 4(30), eaaw6326. DOI: 10.1126/scirobotics.aaw6326
[14] van Nes, N., Brandenburg, S., Twisk, D. (2010). Improving homogeneity by dynamic speed limit systems. Accident Analysis & Prevention, 42(3), 944–952. https://doi.org/10.1016/j.aap.2009.05.002
[15] Yu, R., Abdel-Aty, M. (2014). An optimal variable speed limits system to ameliorate traffic safety risk. Transportation Research Part C: Emerging Technologies, 46, 235–246. https://doi.org/10.1016/j.trc.2014.05.016
[16] Pauer, G., Sipos, T., Török, Á. (2019). Statistical Analysis of the Effects of Disruptive Factors of Driving in Simulated Environment. Transport, 34(1), 1–8. https://doi.org/10.3846/transport.2019.6724
