Csonka Pál Doktori Iskola 

BME Építészmérnöki Kar, Morfológia és Geometriai Modellezés Tanszék

Témavezető: Dr. Domokos Gábor

Térkitöltő mintázatok, mint geometriai modellek

A kutatási téma néhány soros bemutatása

Mindennapjainkban körülvesznek bennünket a térkitöltő mintázatok: elég csak egy kőfal rajzolataira, egy térképre, egy méh-kaptárra vagy egy repedezett sziklára gondolnunk. Munkám során ezeket a természetes és mesterséges mintázatokat vizsgálom a geometria szemüvegén keresztül. A matematikai leírás előnye, hogy feltárulnak vele az általános összefüggések melyek segítségével egy ilyen mintázat jelenlegi képéről következtethetünk annak múltjára vagy akár jövőjére is. Jelenleg a Pennsylvaniai Egyetem kutatóival a Naprendszer égitestein lefotózott repedésmintázatokat, a Berni és Sanghai Egyetem kutatóival az elektronmikroszkóppal megfigyelhető molekuláris mintázatokat tanulmányozzuk. Érdekes látni, hogy bár a lépték nagyon eltér, a geometriai modellek mindkét esetben hatékonyan működnek.

A jelen pályázatban ismertetett munka doktori kutatásomon (mely a konvex poliéderek mechanikai egyensúlyainak vizsgálatával foglalkozik) felül, azt meghaladó tevékenység keretében készült és készül.

 

A kutatóhely rövid bemutatása

 

Kutatásomat az ELKH-BME Szilárd Testek Morfodinamikája Kutatócsoport tagjaként végzem. A csoport fő profilja a természetben és mesterséges környezetben megjelenő formák és mintázatok matematikai és fizikai modellezése, a modellek geofizikai, planetológiai, városépítészeti és kémiai alkalmazásai. A kutatócsoport több tagjával együtt a Morfológia és Geometriai Modellezés Tanszéken dolgozom, ahol az építészetben megjelenő geometriai témaköröket tanítjuk a hallgatóságnak.

 

A kutatás történetének, tágabb kontextusának bemutatása

 

A természetben mindig fellelhetőek voltak a különböző térkitöltő mintázatok, azonban az ember alkotta környezetben is egy-egy példájuk több mint húszezer éves múltra tekint vissza, hiszen ismerünk ilyen régi falazatokat is [B2]. A közlekedés kialakulásával megjelentek az úthálózatok [B4], amelyek a térképre térkitöltő síkbeli mintázatokat rajzoltak. A diszkrét elemekből alkotott, kétdimenziós térkitöltés művészeti eszközként is megjelenik, rengeteg ókori mozaikot hozhatunk fel erre példaként [B5]. A falak az emberi építészet egyik legősibb példái [B2]; velük átlépünk eggyel magasabb dimenzióba, hiszen a fal elemei – kis hézagokkal – kitöltik a 3 dimenziós teret.

De nem csak maguk a térkitöltő mintázatok képezik az emberi kultúra részét évezredek óta, geometriai leírásuk is legalább 2500 éves múltra tekint vissza. Platón nevezetes elméletében az öt szabályos (platóni) testet az öt elemmel azonosította, és ezen elmélet máig meghatározza a tudományos gondolkodás egyes területeit.

A [B6] cikkben Platón fenti elméletének a kockára vonatkozó hipotézisét egy igen érdekes méréssel is tesztelték: 556 darab dolomit fragmenst konvex poliéderekkel közelítve az átlagos lap- és csúcs-számra a (6,03, 8,01) értékeket kapták, melyek meglepő pontossággal közelítik a kocka (6,8) értékeit. Geometriai eszközökkel sikerült belátni, hogy ez az egyezés nem a véletlen műve.

 

A kutatás célja, a megválaszolandó kérdések

 

A térkitöltő mintázatok geometriája önmagában is számos érdekes matematikai kérdést vet fel. Ilyen például, hogy legalább hány éles csúcsa van egy 2-dimenziós vagy egy 3-dimenziós térkitöltő cellának? Célunk a mozaikok átlagtérelméletének 2- és 3-dimenziós fejlesztése hasonló kérdések vizsgálatán keresztül. További célunk ezen elmélet alkalmazási lehetőségeinek feltérképezése.

Az egyes alkalmazási területeken (pl. geológia, kémia, urbanisztika) modelleket állíthatunk fel a mintázatok fejlődésének meghatározására. Célunk, hogy a különböző tudományterületek kutatóival együttműködve geometriai eszközök felhasználásával, eddig nem vizsgált perspektívából szemlélve adjunk magyarázatot a mintázatok jelenlegi képére és időfejlődésére.

Többek között a következő kérdéseket szeretnénk vizsgálni: megállapítható-e geológiai repedéshálózatok képe alapján azok múltja, és megjósolható-e a jövője? Mit mondhatunk ugyanerről várostérképek hálózataival kapcsolatban? Megbecsülhető-e molekuláris mintázatok geometriája a felépítő molekula, és a látott pásztázó elektronmikroszkópos felvételek alapján? Alkalmazható-e a térkitöltő mintázatok átlagtérelmélete más területeken?

 

Módszerek

A mintázatokat úgynevezett normális cellafelbontásokkal modellezzük. Ezek a teret tökéletesen kitöltő cellákból állnak, melyek egymással kizárólag élekben és csúcsokban (csomópontokban) fedhetnek át, és további feltételeknek is meg kell felelniük. Az egy cellához tartozó csúcsok számát v-vel jelöljük, és a cella kombinatorikai fokszámának nevezzük, míg az egy csomópontban átfedő cellák számát n-nel jelöljük, és a csomópont kombinatorikai fokszámának nevezzük [B1]. Ezek a mérőszámok azonban csupán egy mozaik kombinatorikai tulajdonságaira érzékenyek, a cellák formáját nem veszik figyelembe. Ezért bevezettük az n* csomóponti- és a v* cella törés-fokszámokat [A1]. Ezek abban különböznek a korábbi mennyiségektől, hogy a 180°-os szögeket nem számoljuk sem a cella csúcsai közé, sem a csomópontokban találkozó éles szögek közé. Ha egy csomópontban nincsenek 180°-os szögek, akkor regulárisnak, ellenkező esetben irregulárisnak nevezzük (1. ábra).

 

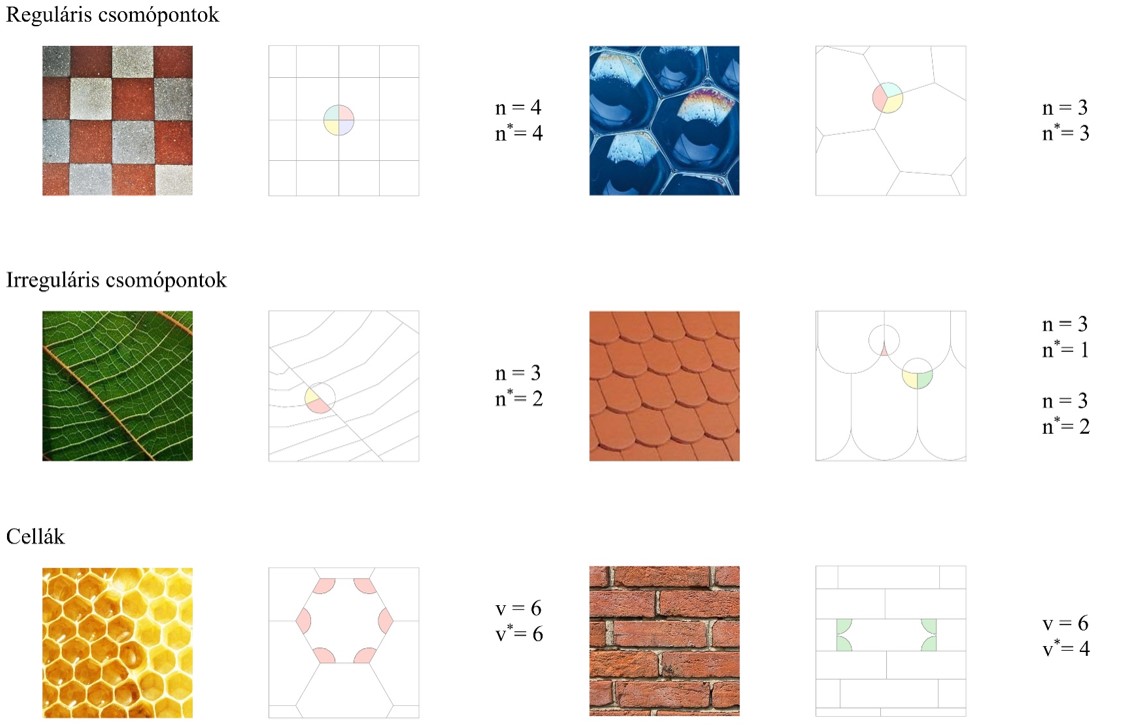
1. ábra Példák csomóponti és cellafokszámok meghatározására

 

A fenti mennyiségeknek a tér (amelyen a mintázat elhelyezkedik) egészére vonatkoztatott  és  átlagaival jellemzünk egy mozaikot. Ezen mennyiségek alapján elhelyezhetjük a mozaikokat az [] metrikus szimbolikus síkon (2. ábra).

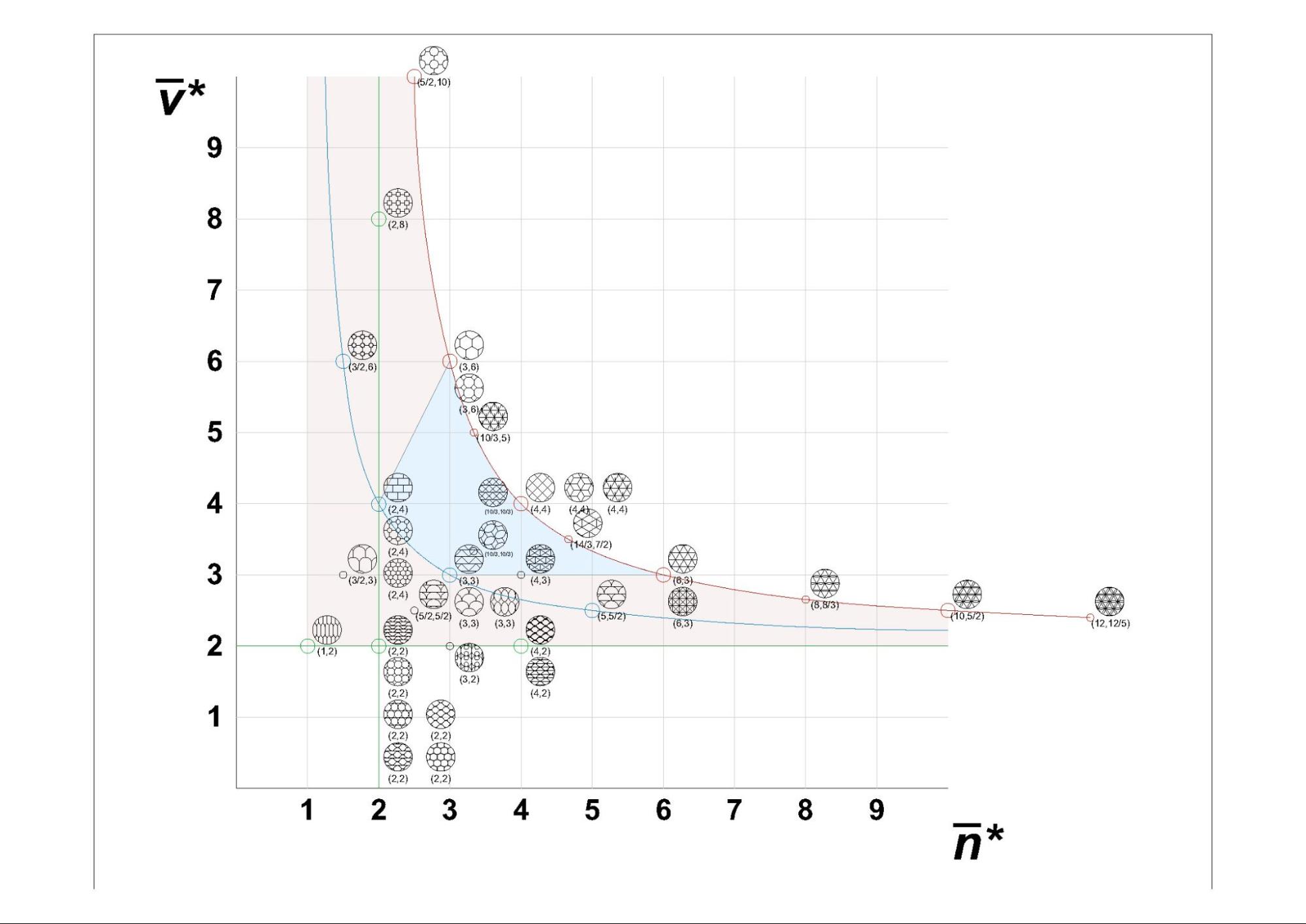
2. ábra Periodikus mozaikok a metrikus szimbolikus síkon

 

A geológiai repedésmintázatok időfejlődését diszkrét, lokális lépések sorozatával modelleztük. Ezen geológiailag kísérletileg igazolt lépésekhez hozzá tudjuk rendelni a cella és csomóponti fokszámok változásait. Ilyen lépés például egy cella kettérepedése, aminek hatására 1 új cella, 2 új csomópont és 1 új él keletkezik. Ha a lépésekhez valószínűségeket társítunk, és a mozaikot egy körön belül vizsgáljuk, mely kör sugara a végtelenhez tart, akkor a modell (a diszkrét lépések időzítésére megfelelően megválasztott véletlen folyamat esetén) folytonos idejűvé válik, és a repedéshálózat időfejlődését a szimbolikus síkon sima trajektóriák fogják jellemezni, melyek általában torlódási ponttal rendelkeznek. Ezen torlódási pontok geológiai szempontból különösen érdekesek.

 

Egyrétegű molekuláris mintázatokra is alkalmaztuk a mozaikok átlagtérelméletét. Itt a különböző nagyításban megfigyelhető mintázatokat jól elkülönült, úgynevezett szinteken elemeztük: A legalsó szint (level 1) maga az anyagot felépítő molekula, melyről geometriai és kémiai információink vannak, a legmagasabb szint (level 4) pedig az elektronmikroszkóppal már látható kép, melyen a molekulákat 1-1 csomópontként azonosítottuk (6. ábra). E két szélső helyzetről meglévő információink alapján becsléseket fogalmaztunk meg a köztes, mikroszkóppal nem látható és nem ismert szintekre, melyek az anyagtudományi kutatás jelenleg legintenzívebben kutatott területei.

 

Eddigi eredmények

 

A korábban felvetett kérdésre, miszerint hány csúcsa van legalább egy 2 dimenziós térkitöltő cellának, az [A1] cikkben társszerzőimmel adott bizonyításunk alapján a válasz 2, és három dimenzióban is megállapítottuk, hogy az alsó korlát 0. A 2 dimenziós bizonyításhoz létrehoztunk egy úgynevezett deregularizáló algoritmust, mely mintázatokat alakít át irreguláris csúcsokat létrehozva, minél távolabb haladva a reguláris állapotuktól (3. ábra).

 

 

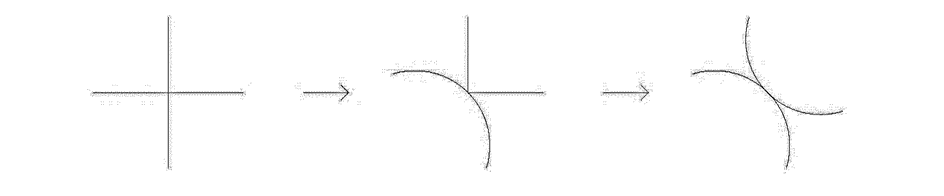
3. ábra A deregularizáló algoritmus működése egy példán bemutatva

 

A Földön megjelenő elsődleges repedésmintázatokra vonatkozó általános modellt tárgyal a [B6] cikk. Erre támaszkodva az [A2] cikkben egy diszkrét, két lépésből álló evolúciós modellt fogalmaztunk meg. Az R0 lépés a másodlagos repedéseket jelképezi, az R1 lépés pedig egy repedésátrendeződés, amikor a „T” csomópontok „Y” csomópontokká alakulnak. (4. ábra)

 

 

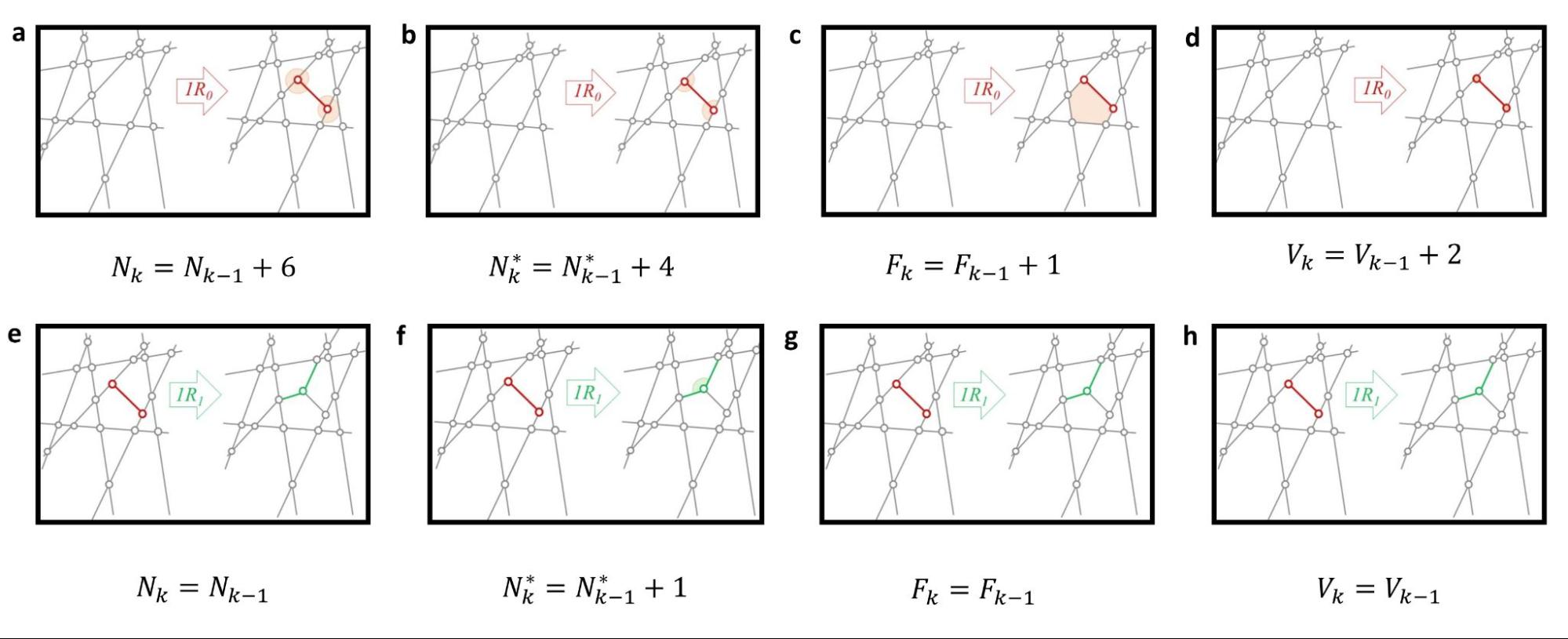
4. ábra Változások egy mozaikban R0 (a,b,c,d) vagy R1 (e,f,g,h) lépések esetén. N a szögek számát, N* a 180°-tól különböző szögek számát, F a lapok számát, V pedig a csúcsok számát jelöli.

 

A fentiek alapján a diszkrét dinamika torlódási pontja meghatározható: , ahol p az R1, (1-p) pedig az R2 lépés valószínűsége. A dinamika segítségével kiszámíthatók adott p valószínűségre a mozaik fejlődését leíró trajektóriák a szimbolikus síkon (5. ábra)

 

 

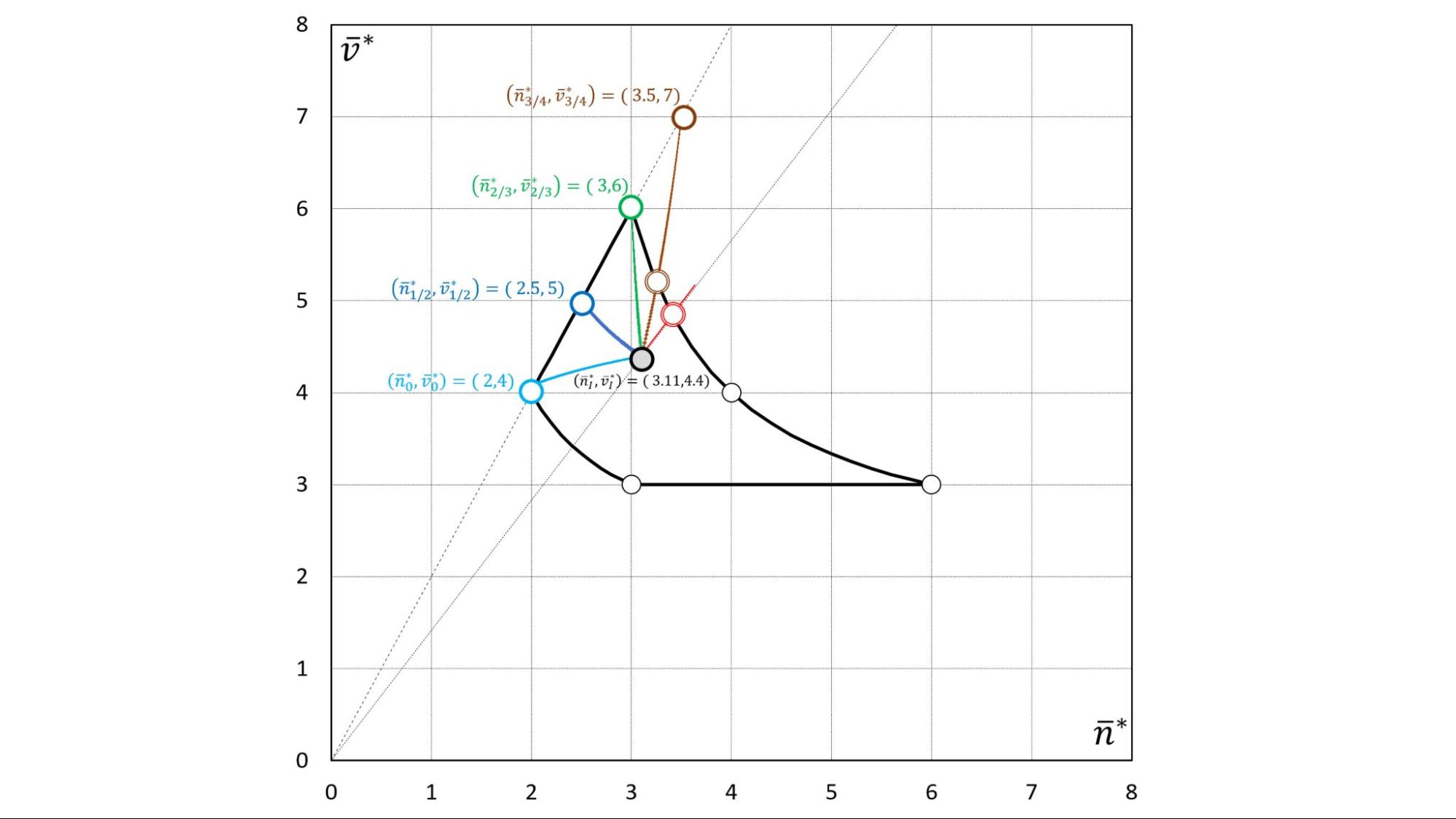
5. ábra Numerikus szimulációk különböző p értékek esetén (p = 0, 1/2, 2/3, 3/4, 1).

Trajektóriák () = (3.11,4.4) kiindulási mozaikkal.

 

Ezt a modellt az [A4] kéziratban fejlesztettük tovább folytonos idejű modellé.

 

Az [A3] cikkben egyrétegű, hidrogénkötéses molekulamintázatokat vizsgáltunk. Jelenleg a rendelkezésünkre álló eszközökkel (pl. pásztázó elektronmikroszkóp) az anyagok pontos szerkezete nem ismerhető meg a kívánt pontossággal, ehhez hosszas szuperszámítógépes számítások szükségesek. Geometriai módszerrel sikerült a mikroszkóppal fel nem tárható tartományra egzakt becsléseket megfogalmaznunk. (6. ábra)

 

 

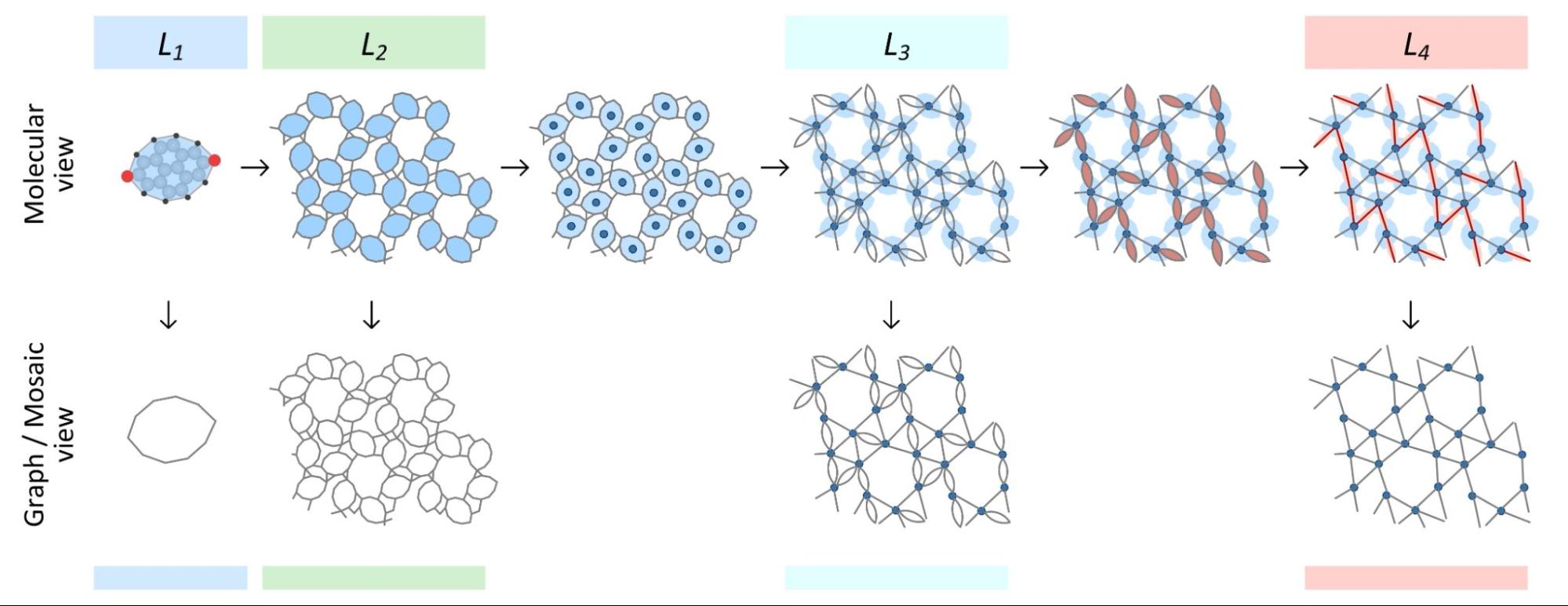
6. ábra A szintek (level 1, 2, 3 és 4) illusztrációi a 2,7-pyrenedione molekulán keresztül.

 

 

Mivel ezek a molekuláris mozaikok kivétel nélkül regulárisak, ezért mind a hiperbolán helyezkednek el. Emiatt elegendő vagy csak a csomóponti, vagy csak a cella-fokszámot megbecsülni. A becslések a szimbolikus síkon a hiperbolán lévő tartományokat határoznak meg. (7. ábra)

 

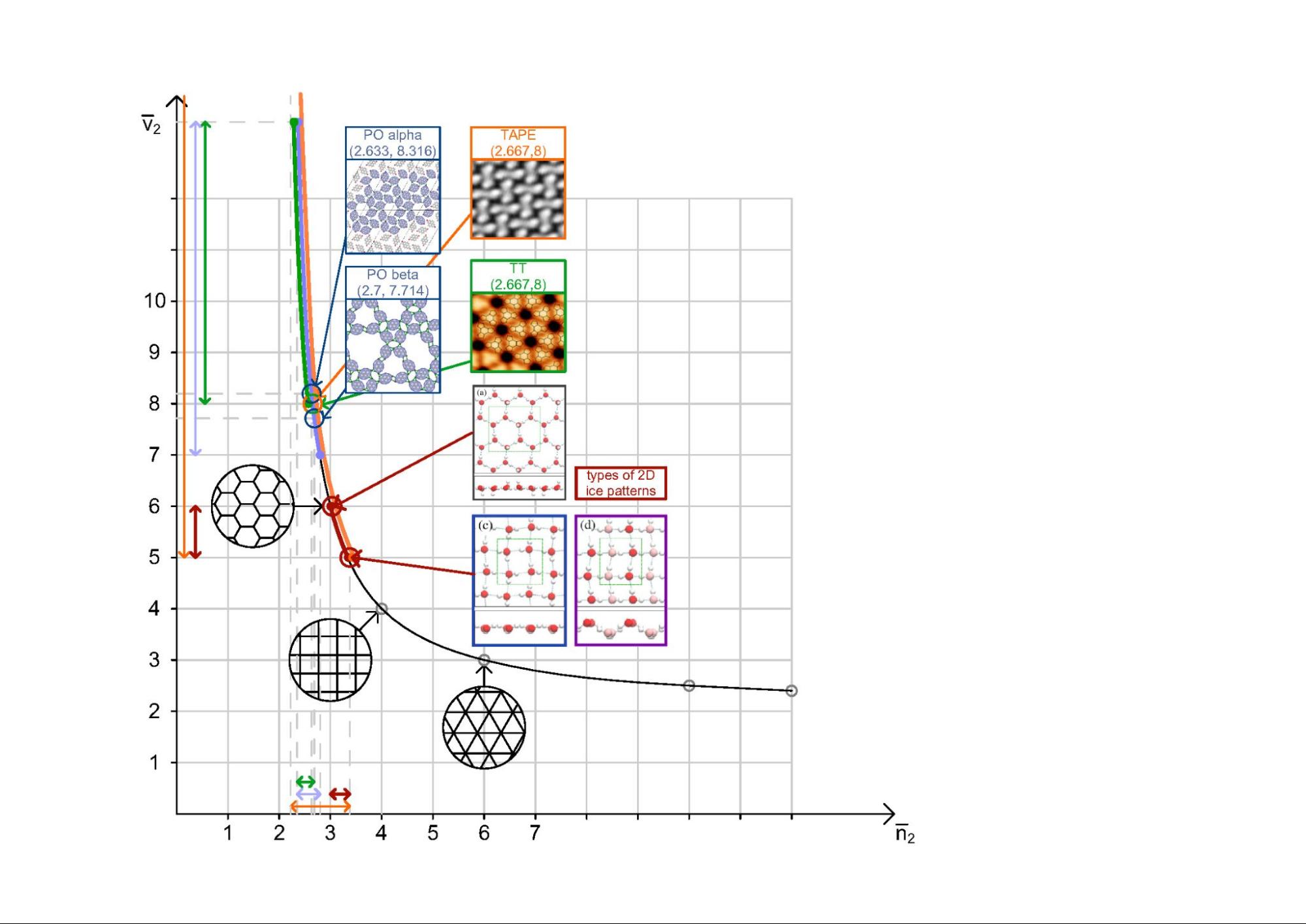
7. ábra L2 szintű mintázatok a szimbolikus síkon, a hozzájuk társított tartományokkal. A 2 dimenziós jég mintázatai a megállapított tartomány mindkét végpontján megjelennek.

 

A 7. ábrán is látható, hogy vannak olyan anyagok, melyek tartományai nem érnek össze, ezeket kombinatorikailag különálló anyagoknak nevezzük. Találtunk olyan molekulát is, mely a becsült tartomány mindkét szélén lévő pontnak megfelelő mintázattal is megjelenik. Ez azt jelenti számunkra, hogy a becsléseink élesek, és nem javíthatóak.

 

Várható impakt, további kutatás

 

Elméleti szempontból érdekes kérdés a 3 dimenziós mintázatok geometriai vizsgálata, átlagtérelméletük továbbfejlesztése.

Lenyűgöző, hogy a geometria nyelve mennyire általános, milyen látszólag távoli jelenségek között teremthet kapcsolatot. Célom ezen területek alaposabb vizsgálata és bővítése. Az alkalmazások területén geológiai szempontból a lépések valószínűségének finomítását, általános modell létrehozását tűztük ki célul. Ebbe a modellbe városfejlődési lépések is implementálhatóak.

A molekuláris mintázatok terén eddig hidrogénkötéses anyagokra fejlesztettük ki a modellünket; célunk, hogy más típusú kötések esetén is meg tudjuk becsülni a lehetséges mintázatok pontos geometriáját.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája:

[A1] G. Domokos, K. Regős, Á. G. Horváth: A two-vertex theorem for normal tilings. Aequantiones Mathematicae, 97, 185–197 (2023). https://doi.org/10.1007/s00010-022-00888-0

[A2] Domokos, G., Regős, K. A discrete time evolution model for fracture networks. Cent Eur J Oper Res (2022). https://doi.org/10.1007/s10100-022-00838-w

[A3] K. Regős, R. Pawlak, X. Wang, E. Meyer, S. Decurtins, G. Domokos, K. S. Novoselov, S. Liu and U. Aschauer, Polygonal tessellations as predictive models of molecular monolayers, 2023, Proceedings of the National Academy of Sciences, e2300049120, 120, 16, https://doi.org/10.1073/pnas.2300049120

[A4] P. Bálint, G. Domokos, K. Regős, An evolution model for polygonal tessellations as models for crack networks and other natural patterns, https://arxiv.org/abs/2301.09503

[A5] Regős Krisztina - Térkitöltő mintázatok geometriai modelljei, szakdolgozat, 2022

 

 

Linkgyűjtemény:

https://www.quantamagazine.org/the-simple-geometry-that-predicts-molecular-mosaics-20230621/

https://forbes.hu/extra/30per30-2023/#/person/22-regos-krisztina

https://docs.google.com/spreadsheets/d/1DW1-SnQ6rKslPjfJQh0h_aKAJwWXlRcFZcrCqi0fi1E/edit?usp=sharing

 

 

Hivatkozások listája:

[B1] Gábor Domokos, Zsolt Lángi. On Some Average Properties of Convex Mosaics. Experimental Mathematics, 2019, DOI: https://doi.org/10.1080/10586458.2019.1691090

[B2] Kyparissi-Apostolika, N. (1999). The Palaeolithic deposits of Theopetra Cave in Thessaly (Greece). British School at Athens Studies, 3, 232–239. http://www.jstor.org/stable/40960232

[B3] Domokos, G., Lángi, Z. Plato’s Error and a Mean Field Formula for Convex Mosaics. Axiomathes (2019). https://doi.org/10.1007/s10516-019-09455-w

[B4] https://www.sevenchurches.org/wp-content/uploads/2020/04/Roman-Road-System-Mediterranean-LGC-Wilson.pdf

[B5] Müller, V. (1939). The Origin of Mosaic. Journal of the American Oriental Society, 59(2), 247–250. https://doi.org/10.2307/594065

[B6] Gábor Domokos, Douglas J. Jerolmack, Ferenc Kun, and János Török. Plato's cube and the natural geometry of fragmentation. Proceedings of the National Academy of Sciences, 117(31):18178–18185, 2020.

 

 

.