
|
BMe Kutatói pályázat |

|
Csonka Pál Doktori Iskola
Szilárdságtani és Tartószerkezeti Tanszék
dr. Sajtos István
Geometriai módszer alkalmazása gömbhéjak horpadásának vizsgálatához
A kutatási téma néhány soros bemutatása
A kutatás során a koncentrált erővel vagy megoszló teherrel terhelt teljes gömbhéj stabilitásvesztésével, a horpadással foglalkozunk. A horpadás jelenségkörében több kérdés nincs még kellően tisztázva. Megfigyelhető, hogy a horpadáshoz tartozó teherrel kapcsolatos elméleti és kísérleti eredmények eltérnek, illetve egy gömbhéjat vizsgálva több, eltérő jellegű horpadási alak is lehetséges, melyek közül ugyanaz a héj esetenként többfélét is felvehet. Számos esetben tapasztalható az is, hogy a horpadt gömbhéj tehermentesítés után is megtartja alakváltozott állapotát. Ezekre a jelenségekre, az ezekhez kötődő kérdésekre kísérelünk meg magyarázatot, választ adni.
A kutatóhely rövid bemutatása
A Szilárdságtani és Tartószerkezeti Tanszék szerkezetek tervezésével, méretezési problémák széles körével foglalkozik. A kutatási témák acél-, fa-, vasbeton, falazott és kompozit szerkezetekkel kapcsolatosak. Ezen túl morfológiai, topológiai problémák, héjszerkezetek stabilitásának vizsgálata is részét képezi a kutatási tevékenységnek, részben elméleti, részben gyakorlati szempontból. Eddig 17 sikeres PhD-védés volt a tanszéken.
A kutatás történetének, tágabb kontextusának bemutatása
Héjaknak nevezzük a görbült középfelületű, viszonylag kis vastagsággal rendelkező felületszerkezeteket. Ezek a mérnöki gyakorlatban számos helyen előfordulnak, például kupolák (1. ábra), silók, tartályok, nyomástartó edények, közúti, légi (2. ábra) és vízi járművek, mikrokapcsolók formájában. A héjakhoz hasonló felépítésű és viselkedésű szerveződések a természetben is sok esetben megfigyelhetők, amire példaként említhetők az őssejtek (3. ábra), az egysejtű élőlények, a baktériumok (4. ábra) vagy a szervek (szív, keringési rendszer). A mérnöki szerkezeteknél gyakran számolni kell a stabilitásvesztés veszélyével, azaz a szerkezetet leíró geometria változása következtében fellépő hirtelen teherbírás-változással. A héjak stabilitásvesztése a horpadás. A héjak horpadási teherbírásának meghatározása nem egyszerű és nem is teljesen kidolgozott feladat. Az elméleti és kísérleti eredmények között fennálló különbség nem feltétlenül csak a kísérletekben megjelenő alakhibák következménye, hanem az elméleti modellek hiányosságaiból is eredeztethető.

1. ábra

2. ábra
3. ábra
4. ábra
A. V. Pogorelov az 1950-es években dolgozta ki az úgynevezett
geometriai héjhorpadás-elméletet. Bár kidolgozása óta ismert a kutatók előtt, alkalmazhatóságát korlátozta az, hogy a horpadt alak meghatározását,
felvételét főként csak kísérletekre alapozták. Az utóbbi 10 évben főként a
fizikusok használták Pogorelov elméletét, akik a héjfelület horpadt alakjának
meghatározását már matematikai alapokra helyezték, azonban a héj
teher-elmozdulás diagramját főként kvalitatívan vizsgálták. Mérnöki szempontból
a horpadási teher és alak kvantitatív meghatározása is fontos.
A kutatás célja, a megválaszolandó kérdések
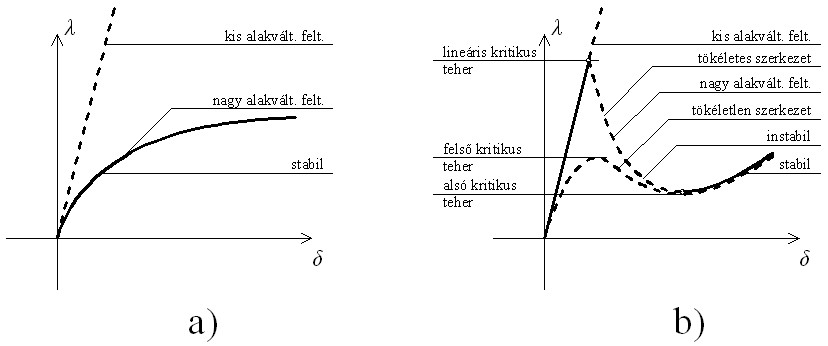
A kutatás fő célja elsősorban a gömbhéjak teher-elmozdulás diagramjának meghatározása a Pogorelov-féle geometriai héjhorpadás-elmélet alapján. A teher-elmozdulás diagram meghatározása azért fontos, mert az ezen szereplő nevezetes pontok megfelelnek a héj horpadási terhének. A valódi (nem tökéletes) héjak viselkedését leíró teher-elmozdulás diagram (5. ábra) jellemzően egy maximum- és egy minimumhellyel rendelkezik, melyekhez tartozó teherértékek elnevezése felső- és alsó kritikus teher. Az elméleti (tökéletes) héj teher-elmozdulás diagramjának maximumhelye a lineáris kritikus teher, ennek sokszor csak töredékét éri el a valóságos héj.
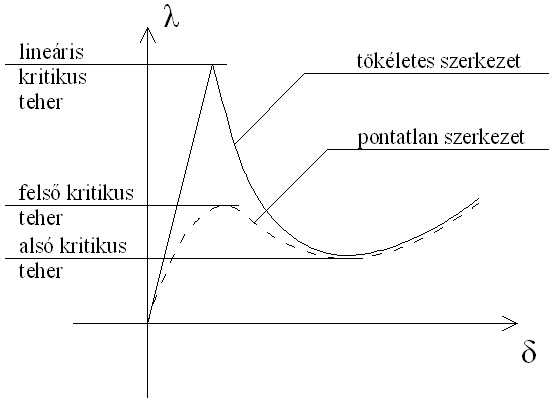
5. ábra
A horpadási teher meghatározásakor figyelembe kell venni, hogy a
horpadás során a horpadási alaknak nemcsak a mérete változhat, hanem a formája,
jellege is. Gömbhéjak esetén ez azt jelenti, hogy bizonyos esetben a horpadási
alak kör alakú, azaz forgásszimmetrikus, míg más esetekben sokszög alakú, azaz
diszkrét fogásszimmetriával rendelkezik, amelynek a ciklusszáma (azaz a sokszög
oldalainak száma) változhat akár a teher növekedésével is. A horpadási alakot
a héj méretei, rugalmassági adatai, megtámasztási viszonyai, a
teher jellege és intenzitása határozhatják meg. A kutatás fontos célja tehát annak meghatározása
is, hogy adott körülmények között milyen horpadási alakok jöhetnek létre. Ezen
alakoknak a teher-elmozdulás diagramon különböző egyensúlyi utak, illetve
egyensúlyi felületek felelnek meg, ezek összemetsződései elágazásokat, az egyes
alakok közti átmenetet jelenthetnek.
Várhatóan e vizsgálatok alapján
megadhatók azok a görbületi és méretviszonyok, illetve teherfajták, amelyek
estén lehetséges negatív horpadási teher. Ezzel igazolhatóvá válhat az a
tapasztalat – melynek egyértelmű elméleti alátámasztása még nem létezik –, hogy
tehermentesítéskor a rugalmas anyagú héj gyakran nem tér vissza, nem pattan
vissza eredeti helyzetébe. Ennek igazolása szintén fontos célja a
kutatásnak.
Módszerek
A kutatás során a horpadási alak egyre pontosabb figyelembevétele vált
indokolttá. A kutatás kezdete a Pogorelov által az 1950-es években kidolgozott, a kutatók által ma is használt
módszerhez, az úgynevezett geometriai héjhorpadás-elmélethez kapcsolódik. Ez alapján a héj egyensúlyi helyzetei
energiamódszerrel kereshetők úgy, hogy a gömbhéjfelület horpadási alakja –
közelítésként – az eredeti gömbfelület izometrikus transzformáltjához közeli
alak [3].
Fizikai értelemben egy felület izometrikus transzformáltja a
felület nyúlásmentes alakváltozások mellett előállítható formája. Ez azt
jelenti, hogy a felület alakját nyújtás, összenyomás, bevágás és torzítás
nélkül, pusztán hajlítással változtatjuk meg, mint például egy papírlap
hajtogatása esetén. Általában a héjakra igaz, hogy – kis vastagságuk
következtében – hajlítómerevségük jóval kisebb, mint a felület adott helyen vett
érintősíkjába eső hatásokkal (nyúlás, szögtorzulás) szembeni merevségük. Így
indokolható azt feltételezni, hogy a héj nagyrészt nyúlásmentes alakváltozásokat
szenved a horpadás során.
A kutatás elején Pogorelov módszerének kis
módosításokkal történő alkalmazásával sikerült néhány egyszerűbb esetben
meghatározni a teljes gömbhéj teher-elmozdulás diagramját, ezáltal a héj
horpadási terhét [1], [2]. A horpadási alak ekkor az eredeti gömbfelület egy
részének inverziójával előállítható izometrikus transzformált alak volt (6.
ábra), ez forgásszimmetrikus horpadási alakot jelentett, ahol a horpadt rész
pereme kör.

6. ábra
Ezt követően izometrikus transzformált alak helyett ahhoz közeli,
de az eredeti felületnek már nyúlásmentes alakváltozásokkal nem előállítható
formájaként határoztuk meg a horpadt alakokat. Ezek az alakok a kísérletek során
is megjelennek, és általában úgynevezett diszkrét forgásszimmetriával
rendelkeznek, azaz valamilyen szabályos sokszöghöz hasonlít a horpadási élek
hálózata (7. ábra). Ilyen alakokat bárki megfigyelhet egy pingponglabdánál.
Megválaszolandó az a kérdés, hogy adott körülmények között milyen alakot vesz
fel a horpadt héj. Eleinte egyszerűsítésként elhanyagoltuk a nyúlási
alakváltozási energiát azokban az esetekben is, ahol az nyilvánvalóan fellépett,
és a horpadási alakot sík lapok által alkotott gúlával közelítettük. Az így
kapott eredmények azt mutatták, hogy a különböző szabályos sokszögekkel jellemezhető
horpadási alakokhoz tartozó görbék a teher-elmozdulás diagramon nem esnek egybe,
de egymáshoz viszonylag közel helyezkednek el, ezért pontosabb vizsgálat
szükséges.

7. ábra
Ez a felismerés indokolta, hogy a nyúlási alakváltozási energiát is
figyelembe kell venni, hogy pontosabb eredményhez jussunk. Ezzel párhuzamosan
alakult ki, hogy a horpadási alakot nem csak egy változó jellemzi, hanem három
[4]. A jelenlegi modellben a horpadási alakot a következő változók írják le: a
horpadás középpontjának mélysége, az úgynevezett belső kör (a horpadt rész
közepén elhelyezkedő, az eredeti gömbfelület egy részének inverziójával
előállítható felületdarab) sugara, és a horpadási sokszög oldalszáma (8. ábra).
A változók száma indokolja, hogy numerikus módszer segítségével keressük az
egyensúlyi helyzeteket. A teher-elmozdulás diagramon nem görbéket alkotnak az
egyensúlyi helyzetek, hanem egyensúlyi felületek alakulnak ki (9. ábra).
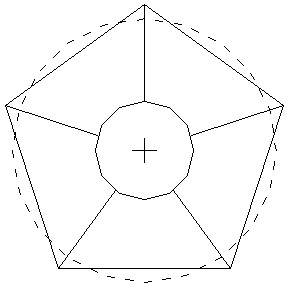
8. ábra
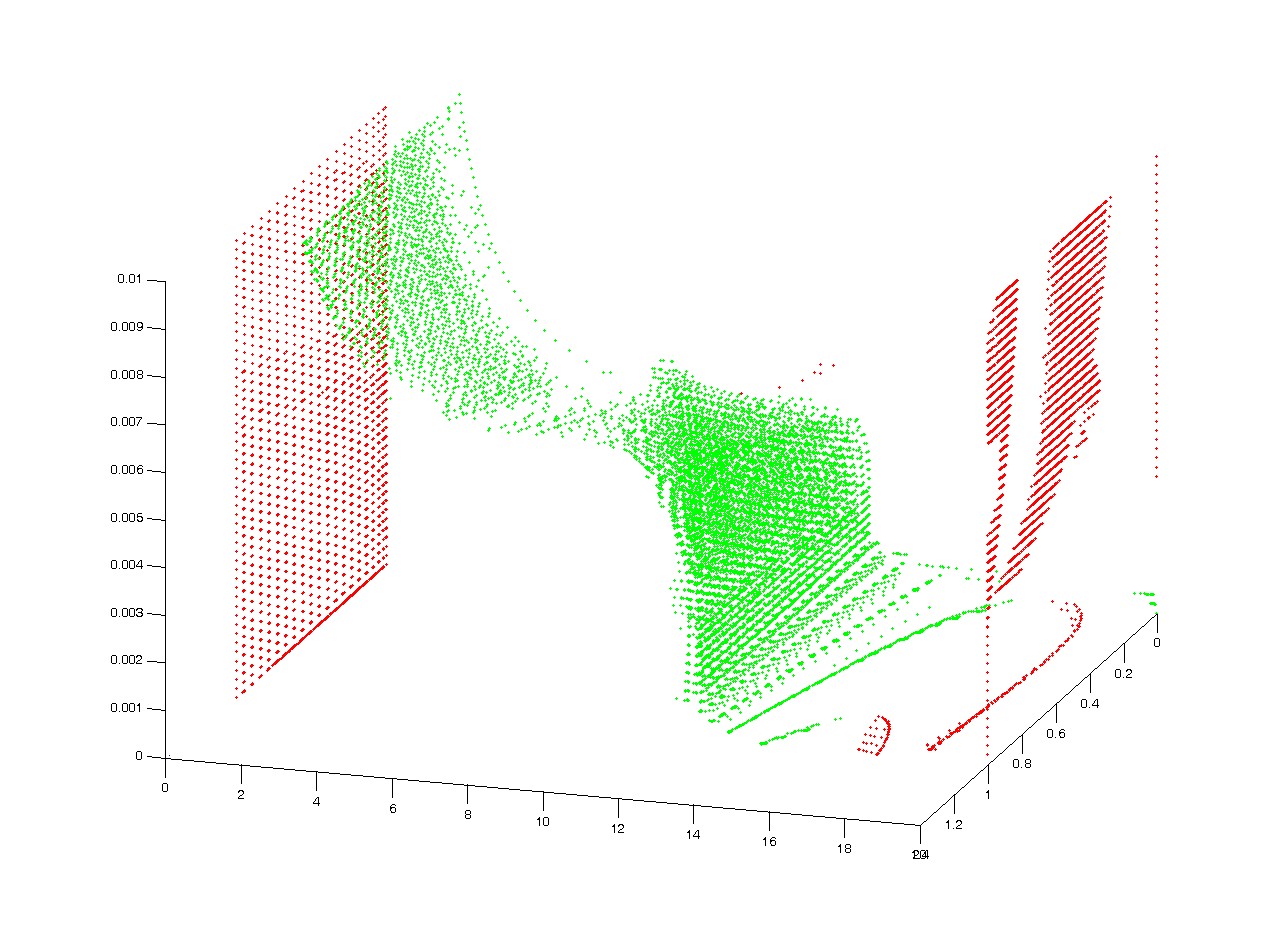
9. ábra
Eddigi eredmények
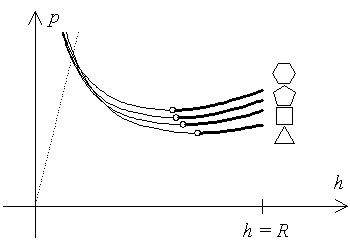
A kutatás kezdetén forgásszimmetrikus horpadási alakot feltételeztünk, tehát a gömbhéj horpadt alakját az eredeti héjfelület egy részének izometrikus transzformáltjaként vettük fel. Az eredmények, amelyeket ezzel a feltételezéssel kaptunk, a párhuzamos, egyenletesen megoszló teher esetében észrevehetően különböznek a Pogorelov által közöltektől. Ennek az az oka, hogy Pogorelov simuló forgásparaboloiddal közelítette a horpadt alakot, ami valójában – legalábbis a feltételezés szerint – az eredeti gömb inverziójával, tükrözésével kapható, tehát gömb. Fontosnak tartjuk, hogy sikerült azt tisztázni, hogy koncentrált teher esetén a gömbhéj emelkedő teher-elmozdulás diagrammal rendelkezik (10.a ábra), míg párhuzamos, egyenletesen megoszló teher, illetve radiális, egyenletesen megoszló teher esetén egy minimumhellyel rendelkezik a függvény (10.b ábra).
10. ábra
Az ezt követő kutatási munkában izometrikus transzformált alak
helyett ahhoz közeli, de az eredeti felületnek már nyúlásmentes
alakváltozásokkal nem előállítható formájaként határoztuk meg a nem
forgásszimmetrikus horpadt alakokat. A vizsgálatok során először a nyúlási
alakváltozási energiarészeket elhanyagoltuk. A különböző szabályos sokszögekkel
jellemezhető horpadási alakokhoz tartozó görbék a teher-elmozdulás diagramon
egymáshoz közel helyezkedtek el (11. ábra), ezeket az eredményeket tartalmazza
[1]. Mindez pontosabb modell alkotását indokolta.
11. ábra
A következő modellben a horpadási alakot több változó írja le: a
horpadás középpontjának mélysége, a horpadt rész közepén elhelyezkedő, az
eredeti gömbfelület egy részének tükrözésével előállítható felületdarab sugara
és a horpadási sokszög oldalszáma. Az egyensúlyi helyzetek nem görbéket alkotnak
a teher-elmozdulás diagramon, hanem egyensúlyi felületeket. Ezek keresése egy,
az ún. gradiens-módszeren alapuló numerikus módszerrel történik. Megemlítendő,
hogy a legújabb változatban már a nyúlási alakváltozási energiarészeket is
tartalmazni fogják az egyenletek.
Várható impakt, további kutatás
A további kutatáshoz szükséges megvizsgálni, hogy az eredmények hogyan alkalmazhatók a
mérnöki problémák és a biológia területén. A horpadási alak
és teherbírás geometriai, szilárdsági paraméterektől és teherfajtától való
függésének további vizsgálata is célként szerepel.
A kísérletekben is
tapasztalható horpadási alakokhoz tartozó teher ismerete pontosítja és
megbízhatóbbá teszi a „gömbből készült” szerkezetek méretezését. A gömbre kapott
eredmények általánosítása lehetővé teszi tetszőleges görbületi viszonyokkal bíró
elliptikus héjfelületek pontosabb horpadásvizsgálatát.
Saját publikációk, hivatkozások, linkgyűjtemény
[1] Vető, D. – Sajtos, I.: Application of Geometric Method to Determine the Buckling Load of Spherical Shells. Pollack Perodica, 4 (2), 123–134. oldal (2009)
[2] Vető, D. – Sajtos, I.: Application of Geometric Method to Determine the Buckling Load of Spherical Shells. ed.: Lehoczky, L.: XXIII. microCAD International Scientific Conference, University of Miskolc, 2009. március 19–20., Miskolc Innovation and Technology Transfer Centre, Miskolc, 61–66. oldal (200.)
[3] Vető, D. – Sajtos, I.: Application of Geometric Method to Determine the Buckling Load of Spherical Shells. ed.: Iványi, M.: Pollack PhD, Fourth International PhD, DLA Symposium, University of Pécs, Pollack Mihály Faculty of Engineering, 2008. október 20–21., Pécs, Rotari Press, Komló, 61. oldal (2008)
[4] Vető, D. – Sajtos, I.: Investigation of Buckling of Spherical Shells.
FUDoM 09, Finno-Ugric International Conference of Mechanics, 2009. augusztus 23–29., Ráckeve, 31–32. oldal
(2009)
