 |
BMe Research Grant |

|
As submitted in October 2010
Faculty of Architecture
Department of Mechanics, Materials and Structures
Fiber Reinforced (Composite) Beams and Columns
Introducing the research area
Composites (fiber reinforced plastics) are already widely used in aerospace industry, in sport equipment and in transportation industry. They are gaining more and more ground in various fields of civil engineering [2]. This is due to their excellent material properties such as high strength to weight ratio, corrosion resistance and high fatigue strength, which may compensate relatively high material prices. Engineering problems encountered by designers working with traditional materials (steel, reinforced concrete) have already been thoroughly researched, however, those working with composites must face new, astonishing challenges and must apply the knowledge in several fields of science and engineering to avoid occurrence of undesired behaviors during the service of composite structures.
Brief introduction of the research place
At the Department of Mechanics, Materials and Structures there are ongoing researches in almost all areas of structural engineering. In addition to composite materials, our investigations include steel, reinforced concrete, masonry, timber or even adobe structures. Stability of structures, large displacements and earthquake engineering also belong to important areas. Members of our department research various practical problems, e.g. shells, high rise buildings and membrane structures. Our research area includes a wide range of mechanics, applied mathematics and population dynamics, but we are also looking for explanations for the shape of pebbles and asteroids.
History and context of the research
Beams and columns are important structural elements and the analysis and design of beams and columns made of traditional materials, such as steel or wood, are standard procedures. However, composite materials offer an attractive alternative due to their advantageous characteristics. Fiber reinforced plastic (FRP) profiles can be manufactured by pultrusion process with relatively low manufacturing cost, and hence, are used extensively worldwide.
As the characteristics of FRP beams and columns differ significantly from those of steel beams, very often designers may not depend on traditional design processes and ‘rules of thumb’. Consequently, it is essential (i) to understand the behavior of composite beams, (ii) to develop new theories, (iii) to set up decision rules for the application of simplified theories, (iv) and to introduce design guides for the engineers.
In the case of beams designed with conventional materials, designers must determine the shape of the cross section including wall thickness. When using composite materials, however, fiber orientation in the beams must also be determined for best carrying the applied load.
As axial stresses reach the highest values in beams and columns, most of the fibers are placed in parallel to the axis of the beam. Besides the benefits in axial load bearing capacity, this orientation is accompanied with two
shortcomings.
In a beam with the most fibers in the axial direction, both the shear
stiffness and shear strength are low. For steel, the Young modulus to
shear modulus ratio is about E/G~2.5, while for glass fiber reinforced epoxy
this ratio is about 10-15, while for a unidirectional graphite epoxy E/G can be as
high as 40. Hence, shear deformation and shear failure are critical considerations
for composite structures.
Additionally, the absence of fibers perpendicular to the axis reduces the
stiffness of the wall segments of beams in this direction, which may lead to
the distortion of the cross section and increases the propensity to local buckling.
When the layup of the beam walls includes (unbalanced)
fibers in off-axis direction (in addition to fabric, mat and fibers in the
axial direction), the beam exhibits axial-torsion and bending-torsion coupling,
i.e. columns subjected to tension or beams subjected to in-plane loads will
twist. Based on classical theories this behavior cannot be predicted.
Aim of the research
Beam theory (with Anikó Pluzsik)
State of the art beam theories are
summarized in [5]. Although several beam theories exist (the most well-known
developed by Bernoulli that assumes plane-deformed cross-section), none of them considers all the relevant effects reviewed above and may be
important for a thin-walled composite beam. In this research, we will provide a
new theory and method to calculate the stiffness matrix for anisotropic
beams.
Local buckling analysis of thin-walled beams (with Gabriella Tarján)
When
thin-walled composite beams or columns are subjected to axial load, bending or
transverse loads their walls may buckle locally. The analysis of local buckling
of FRP members axial loads can be treated with sufficient accuracy [2, 5],
however, the web buckling of transversely loaded beams can only be approximated
by neglecting the restraining effects of the flanges. In this research, the local
buckling of transversely beams under arbitrary loading will be presented.
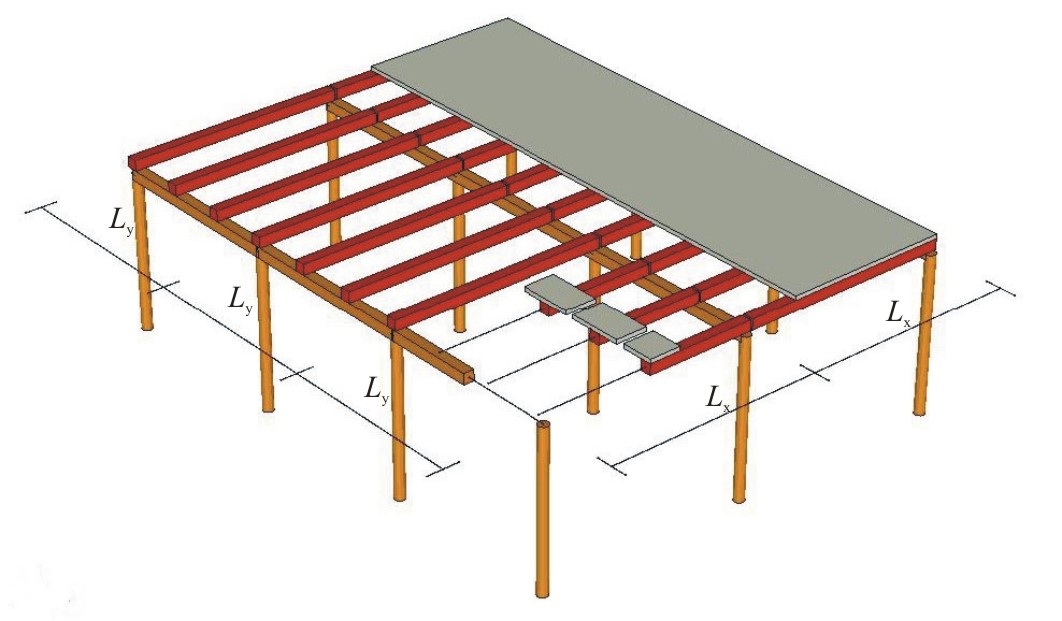
Vibration of composite floors supported by beams (with Béla Kulcsár)
Flat
and rib-stiffened reinforced concrete, composite and timber floors are often
used for residential buildings. For longer spans the limitation of the
applicability is the low natural frequency, which may cause discomfort to
residents. Rib-stiffened plates can be modeled by orthotropic (composite)
plates. For simply supported floors, the natural frequency can be calculated from
the expressions summarized in [5], which are widely used in practice, however, in
many cases they overestimate natural frequency.

FRP confined reinforced concrete columns (with Bernát
Csuka)
Fiber-reinforced plastics (FRP) composites are widely used as FRP
jackets to confine reinforced concrete columns and hence to increase its load
bearing capacity. There are several existing models for the calculation of
concentrically loaded columns, however, experimental and theoretical results
on structures under eccentric loading are rather scarce. Furthermore,
available models significantly overestimate the failure load for eccentrically
loaded columns.
We wish to develop a model that can reasonably predict the
behavior of FRP confined columns under eccentric loading. We will also develop
explicit approximate expressions for design purposes.
Methods
Creation of the new beam theory includes the following steps: first, we will present an analytical solution of the governing differential equations of the beam subjected to trigonometric loads. The solution is developed for both the 1D (beam) and for the 3D (shell) models. The replacement stiffnesses of the beam will be derived directly from the 3D model using limit transition.
Local buckling analysis of members can be performed by treating the wall
segments as long orthotropic plates [2, 9]. The rotation of the long edges is
restrained by the adjacent wall segments. The key process in the analysis is to determine the buckling load of long or short composite plates, where
the edges are elastically restrained [8]. Based on the results, the local buckling
of the segments can be investigated [9].
To investigate the vibration of composite floors, we will (i) combine
analytical solutions of the vibration of composite (sandwich) beams and
(ii) the summation theorems. Results will be verified by experiments.
Simple, explicit expressions to be used easily in
practical design will be developed.
We are going to develop a numerical model for calculating the load-bearing capacity of
FRP confined circular RC cross-sections under eccentric loading, which is based
on a sophisticated concrete model proposed by Papanikolaou and Kappos. Applying this complex numerical model, we hope to explain the behavior of FRP
confined RC columns observed in the literature [10]. The results are also
verified by experiments.
Results
We developed a beam theory [5, 6] that takes into account the
axial-torsion and bending-torsion coupling. We also generalized the classical
(in-plane) shear deformation theory for beams subjected to both in-plane loads
and torsion [5].
Since stiffness of composite walls are relatively low
and the walls are thin, buckling is a major consideration in design. Long beams
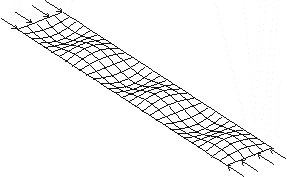
subjected to axial load buckle globally by flexural torsional buckling, while
long beams subjected to in-plane load buckle by lateral torsional buckling as
illustrated in the figure below. These problems were solved in [1, 5].

The shorter the beam, the thinner the walls and the lower the stiffness perpendicular to the axis of the beam, the more likely that local buckling occurs first, as illustrated for the top flange of a box section beam.
According to several researchers, design of composite beam sections is
governed by local buckling. Exact analysis results in transcendental equations
which are too tedious for design purposes. By making a significant yet
mechanically acceptable simplification, we have derived simple expressions for
calculating the local buckling loads of composite beams subjected to axial load
and bending, which may be applied easily in the design of the cross section [2,
5].

Application of beam theories
Beams are used in many practical applications, e.g. in airplanes or in building constructions, but several other fields exist where beam theories are applicable in the analysis.
Alpine skies and snowboards are made with sandwich construction using FRP
materials. Skies and snowboards are usually designed empirically using
prototypes, laboratory and field tests. We have developed a model for analyzing the
performance of the snowboards, which enable us to reduce the number of required tests
[4].
Approximate vibration analysis may play an important role in
the preliminary design of building structures and also in their final design
for the verification of the more sophisticated finite element models. One of the
most effective approximate methods is the continuum (beam) analysis, which was
successfully applied for earthquake analysis of building structures [3].
Expected impact and further research
The beam theory we developed can be used in the design of pultruded sections (beams and columns), wind turbine blades, golf shafts etc. Using this model enhances accuracy of analyses, and hence safer or cheaper structures can be designed.
The simple local buckling analysis of composite sections and the
vibration analysis of composite floors can be used by the engineers in practical
design. The developed model of confined concrete will hopefully be the only
reliable tool to predict the behaviour of eccentrically loaded columns.
The results published earlier are referred to in the literature, as can be
seen in the KPA (MTMT) database. Perhaps our most intensively used engineering
result is the local buckling analysis of axially loaded columns, which was
recommended for practical application, e.g. in the monograph written by L. Banks
(Composites for Construction, Whiley, 2006).
References
[1] Sapkás, Á and L.P. Kollár: Lateral-torsional buckling of composite beams with shear deformation. International Journal of Solids and Structures, (2002), 39, 2939-2963.
[2] Kollár, L.P: Local Buckling of FRP Composite Structural Members with Open and Closed Cross Sections. Journal of Structural Engineering, (2003), Vol. 129. 1503-1513.
[3] Potzta, G. and L.P. Kollár: Analysis of Building Structures by Replacement Sandwich Beams. International Journal of Solids and Structures, (2003), 40, 535-553.
[4] Brennan, S.M., L.P. Kollár and G.S. Springer.: Modelling the mechanical characteristics and on-snow performance of snowboards. “Sports Engineering” (2003), 6. 193-206
[5] László P. Kollár and George S. Springer: Mechanics of Composite Structures. Cambridge University Press. 2003. (p. 490)
[6] Pluzsik A. and Kollár L.: Analysis of closed section composite beams, International Journal of Solids and Structures. 43 (17) , 2006, 5307-5336.
[7] Kollár, L.P.: Composites in the Infrastructure. Journal of Reinforced Plastics and Composites 2008, 27: 1229-1231
[8] Tarján, G., A. Sapkás and L.P. Kollár: Stability Analysis of Long Composite Plates with Restrained Edges Subjected to Shear and Linearly Varying. Journal of Reinforced Plastics and Composites, 2010, 29: 1386-1398
[9] Tarján, G., A. Sapkás and L.P. Kollár: Local Web Buckling of Composite (FRP) Beams. Journal of Reinforced Plastics and Composites, 2010, 29: 1451-1462
[10] Csuka, B and L.P. Kollár: Numerical model for frp confined circular RC cross-sections under eccentric loading. 14th European Conference on Composite Materials 7-10 June 2010, Budapest, Hungary, (p. 10)




