Faculty of Architecture

Department of Mechanics, Materials and Structures

Fiber Reinforced (Composite) Beams and Columns

Introducing the research area

Composites (fiber reinforced plastics) are already widely used in aerospace industry, in sport equipment and in transportation industry. They are gaining more and more ground in various fields of civil engineering [2]. This is due to their excellent material properties such as high strength to weight ratio, corrosion resistance and high fatigue strength, which may compensate relatively high material prices. Engineering problems encountered by designers working with traditional materials (steel, reinforced concrete) have already been thoroughly researched, however, those working with composites must face new, astonishing challenges and must apply the knowledge in several fields of science and engineering to avoid occurrence of undesired behaviors during the service of composite structures. 

Brief introduction of the research place

History and context of the research

Beams and columns are important structural elements and the analysis and design of beams and columns made of traditional materials, such as steel or wood, are standard procedures. However, composite materials offer an attractive alternative due to their advantageous characteristics.   Fiber reinforced plastic (FRP) profiles can be manufactured by pultrusion process with relatively low manufacturing cost, and hence, are used extensively worldwide.

As the characteristics of FRP beams and columns differ significantly from those of steel beams, very often designers may not depend on traditional design processes and ‘rules of thumb’. Consequently, it is essential (i) to understand the behavior of composite beams, (ii) to develop new theories, (iii) to set up decision rules for the application of simplified theories, (iv) and to introduce design guides for the engineers.

In the case of beams designed with conventional materials, designers must determine the shape of the cross section including wall thickness. When using composite materials, however, fiber orientation in the beams must also be determined for best carrying the applied load.

As axial stresses reach the highest values in beams and columns, most of the fibers are placed in parallel to the axis of the beam. Besides the benefits in axial load bearing capacity, this orientation is accompanied with two shortcomings.
In a beam with the most fibers in the axial direction, both the shear stiffness and shear strength are low. For steel, the Young modulus to shear modulus ratio is about E/G~2.5, while for glass fiber reinforced epoxy this ratio is about 10-15, while for a unidirectional graphite epoxy E/G can be as high as 40. Hence, shear deformation and shear failure are critical considerations for composite structures.

Additionally, the absence of fibers perpendicular to the axis reduces the stiffness of the wall segments of beams in this direction, which may lead to the distortion of the cross section and increases the propensity to local buckling.

When the layup of the beam walls includes (unbalanced) fibers in off-axis direction (in addition to fabric, mat and fibers in the axial direction), the beam exhibits axial-torsion and bending-torsion coupling, i.e. columns subjected to tension or beams subjected to in-plane loads will twist. Based on classical theories this behavior cannot be predicted.

Aim of the research

Beam theory (with Anikó Pluzsik)
State of the art beam theories are summarized in [5]. Although several beam theories exist (the most well-known developed by Bernoulli that assumes plane-deformed cross-section), none of them considers all the relevant effects reviewed above and may be important for a thin-walled composite beam. In this research, we will provide a new theory and method to calculate the stiffness matrix for anisotropic beams. 

Local buckling analysis of thin-walled beams (with Gabriella Tarján)
When thin-walled composite beams or columns are subjected to axial load, bending or transverse loads their walls may buckle locally. The analysis of local buckling of FRP members axial loads can be treated with sufficient accuracy [2, 5], however, the web buckling of transversely loaded beams can only be approximated by neglecting the restraining effects of the flanges. In this research, the local buckling of transversely beams under arbitrary loading will be presented.

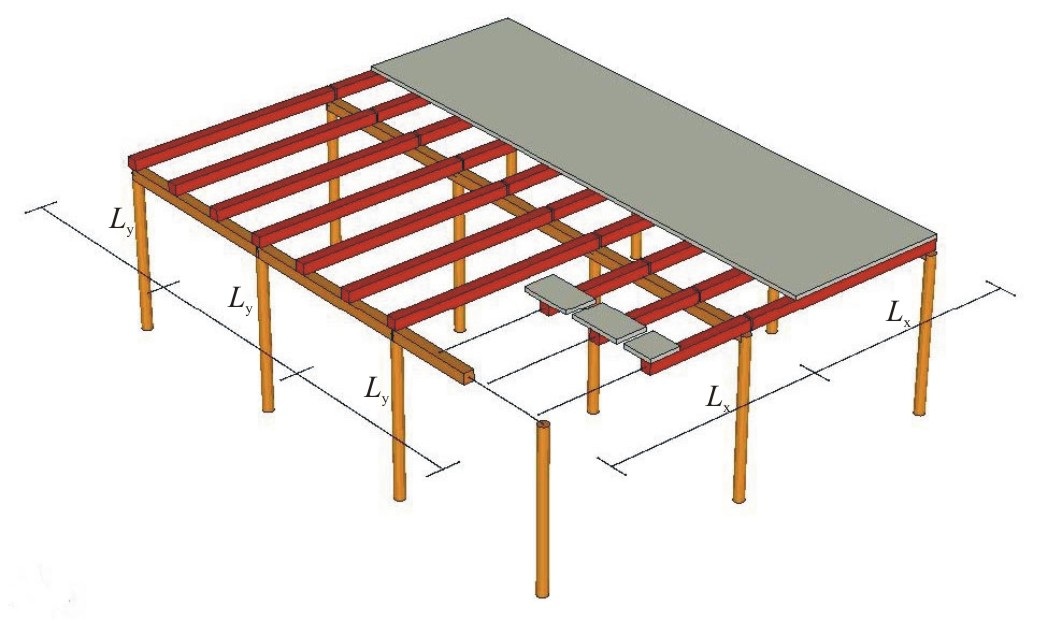
Vibration of composite floors supported by beams (with Béla Kulcsár)
Flat and rib-stiffened reinforced concrete, composite and timber floors are often used for residential buildings. For longer spans the limitation of the applicability is the low natural frequency, which may cause discomfort to residents. Rib-stiffened plates can be modeled by orthotropic (composite) plates. For simply supported floors, the natural frequency can be calculated from the expressions summarized in [5], which are widely used in practice, however, in many cases they overestimate natural frequency.

FRP confined reinforced concrete columns (with Bernát Csuka)
Fiber-reinforced plastics (FRP) composites are widely used as FRP jackets to confine reinforced concrete columns and hence to increase its load bearing capacity. There are several existing models for the calculation of concentrically loaded columns, however, experimental and theoretical results on structures under eccentric loading are rather scarce. Furthermore, available models significantly overestimate the failure load for eccentrically loaded columns.
We wish to develop a model that can reasonably predict the behavior of FRP confined columns under eccentric loading. We will also develop explicit approximate expressions for design purposes.

Methods

Creation of the new beam theory includes the following steps: first, we will present an analytical solution of the governing differential equations of the beam subjected to trigonometric loads. The solution is developed for both the 1D (beam) and for the 3D (shell) models. The replacement stiffnesses of the beam will be derived directly from the 3D model using limit transition.

Local buckling analysis of members can be performed by treating the wall segments as long orthotropic plates [2, 9]. The rotation of the long edges is restrained by the adjacent wall segments. The key process in the analysis is to determine the buckling load of long or short composite plates, where the edges are elastically restrained [8]. Based on the results, the local buckling of the segments can be investigated [9].

To investigate the vibration of composite floors, we will (i) combine analytical solutions of the vibration of composite (sandwich) beams and  (ii) the summation theorems. Results will be verified by experiments. Simple, explicit expressions to be used easily in practical design will be developed.

We are going to develop a numerical model for calculating the load-bearing capacity of FRP confined circular RC cross-sections under eccentric loading, which is based on a sophisticated concrete model proposed by Papanikolaou and Kappos. Applying this complex numerical model, we hope to explain the behavior of FRP confined RC columns observed in the literature [10]. The results are also verified by experiments.

Results

We developed a beam theory [5, 6] that takes into account the axial-torsion and bending-torsion coupling. We also generalized the classical (in-plane) shear deformation theory for beams subjected to both in-plane loads and torsion [5].
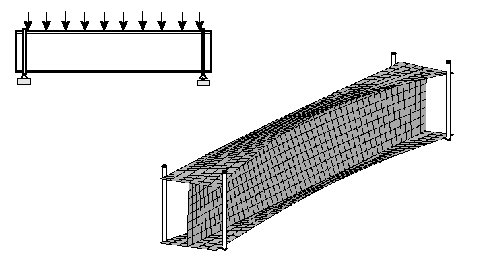
Since stiffness of composite walls are relatively low and the walls are thin, buckling is a major consideration in design. Long beams subjected to axial load buckle globally by flexural torsional buckling, while long beams subjected to in-plane load buckle by lateral torsional buckling as illustrated in the figure below. These problems were solved in [1, 5]. 

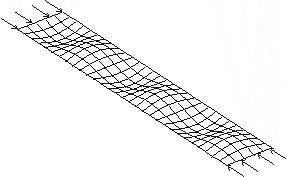
The shorter the beam, the thinner the walls and the lower the stiffness perpendicular to the axis of the beam, the more likely that local buckling occurs first, as illustrated for the top flange of a box section beam.

According to several researchers, design of composite beam sections is governed by local buckling. Exact analysis results in transcendental equations which are too tedious for design purposes. By making a significant yet mechanically acceptable simplification, we have derived simple expressions for calculating the local buckling loads of composite beams subjected to axial load and bending, which may be applied easily in the design of the cross section [2, 5].

Application of beam theories

Beams are used in many practical applications, e.g. in airplanes or in building constructions, but several other fields exist where beam theories are applicable in the analysis.

Alpine skies and snowboards are made with sandwich construction using FRP materials. Skies and snowboards are usually designed empirically using prototypes, laboratory and field tests. We have developed a model for analyzing the performance of the snowboards, which enable us to reduce the number of required tests [4].
 
Approximate vibration analysis may play an important role in the preliminary design of building structures and also in their final design for the verification of the more sophisticated finite element models. One of the most effective approximate methods is the continuum (beam) analysis, which was successfully applied for earthquake analysis of building structures [3].

Expected impact and further research

The beam theory we developed can be used in the design of pultruded sections (beams and columns), wind turbine blades, golf shafts etc. Using this model enhances accuracy of analyses, and hence safer or cheaper structures can be designed.

The simple local buckling analysis of composite sections and the vibration analysis of composite floors can be used by the engineers in practical design. The developed model of confined concrete will hopefully be the only reliable tool to predict the behaviour of eccentrically loaded columns.

The results published earlier are referred to in the literature, as can be seen in the KPA (MTMT) database. Perhaps our most intensively used engineering result is the local buckling analysis of axially loaded columns, which was recommended for practical application, e.g. in the monograph written by L. Banks (Composites for Construction, Whiley, 2006).

References

Introduction of the participants:

Kollár László

Csuka Bernát

Pluzsik Anikó

Tarján Gabriella