Építészmérnöki Kar

Szilárdságtani és Tartószerkezeti Tanszék

Szálerősítéses műanyag (kompozit) rudak

A kutatási terület néhány soros bemutatása

A kompozit anyagokat (szálerősítéses műanyagokat) széleskörűen alkalmazzák a repülőgépiparban, a sporteszközökhöz, a közlekedésben és újabban egyre nagyobb mértékben az építőiparban is [2]. Ez elsősorban kedvező tulajdonságaiknak köszönhető: magas a fajlagos szilárdságuk, jók a fáradási tulajdonságaik, ellenállnak a környezeti hatásoknak, ami kompenzálja a magas anyagárakat. A hagyományos szerkezeti anyagokhoz (pl. acél, vasbeton) szokott tervezőmérnök új kihívásokkal szembesül, ha kompozit szerkezeteket kell terveznie vagy alkalmaznia. Kellő ismeret hiányában kellemetlen meglepetések érhetik. 

A kutatóhely rövid bemutatása  

A kutatás történetének, tágabb kontextusának bemutatása 

A rudak (gerendák és oszlopok) fontos szerkezeti elemek. Ezek tradicionális anyagokkal való méretezése a napi tervezés rutinfeladata. A fent említett kedvező tulajdonságai miatt ma már széleskörűen alkalmaznak kompozit rudakat.

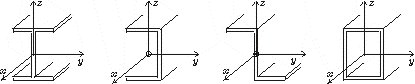
A kompozitok viselkedése jelentősen eltér a hagyományos anyagokétól, ezért a hagyományos tervezési módszerek és „ökölszabályok” nem működnek. Emiatt nagyon fontos, hogy (i) megértsük a kompozitok viselkedését, (ii) új elméleteket fejlesszünk ki és (iii) tervezési módszereket dolgozzunk ki.

Kompozitszerkezetek esetében nemcsak a szerkezet alakját tervezzük meg, hanem a rúdban futó szálak irányát is: úgy helyezzük el őket, hogy a teherbírás a lehető legnagyobb legyen. Gerendákban és oszlopokban a tengelyirányú feszültségek a legnagyobbak, így a szálak többsége is tengelyirányú. Ennek sajnos két hátránya is van.
Ha a szálak zömmel tengelyirányban futnak, akkor a szerkezet nyírási merevsége viszonylag alacsony. Acél esetén a rugalmassági modulus és a nyírási rugalmassági modulus E/G aránya körülbelül  2,5,  üvegszálas epoxi esetén 10-15, egyirányú szálakat tartalmazó grafit epoxi esetében viszont az E/G akár 40 is lehet. Így a nyírási deformáció figyelembevétele alapvető fontosságú.

Ezen kívül csekély mennyiségű keresztirányú szál esetén a keresztmetszet torzulhat és hajlamossá válhat a lokális horpadásra.

Ha a szálak nem kiegyensúlyozott módon vannak elhelyezve, akkor a rúd igen furcsa viselkedést mutat: húzás esetén elcsavarodik és síkbeli terhelésre is térben deformálódik. Ezt a viselkedést a hagyományos rúdelmélet nem képes modellezni.

A kutatás célja, a megválaszolandó kérdések

Rúdelmélet (Pluzsik Anikóval)
A kompozit rúdelméletek összefoglalása megtalálható [5]-ben. Meg kell jegyeznünk, hogy jóllehet számos elméletet publikáltak (a legismertebb a Bernoullitól származó, sík keresztmetszetek elvére alapított elmélet), még sincs olyan rúdelmélet, amely az összes fent felsorolt hatást figyelembe tudná venni. Az a célunk, hogy egy általánosan használható rúdelméletet fejlesszünk ki.

Vékony falú rudak lokális horpadása (Tarján Gabriellával)
Ha vékony falú kompozit rudakat axiálisan terhelünk, hajlítunk vagy nyírunk, akkor a falak (lokálisan) horpadhatnak. A vékony falú rudak horpadása axiális teherre megoldottnak tekinthető [2, 5], de a keresztirányban terhelt rudak horpadása még nem kellően feltárt, és ez nagyon fontos kérdés a gerendák tervezésében. A kutatás keretében végre kívánjuk hajtani az általánosan terhelt rudak lokális horpadásának vizsgálatát.
 

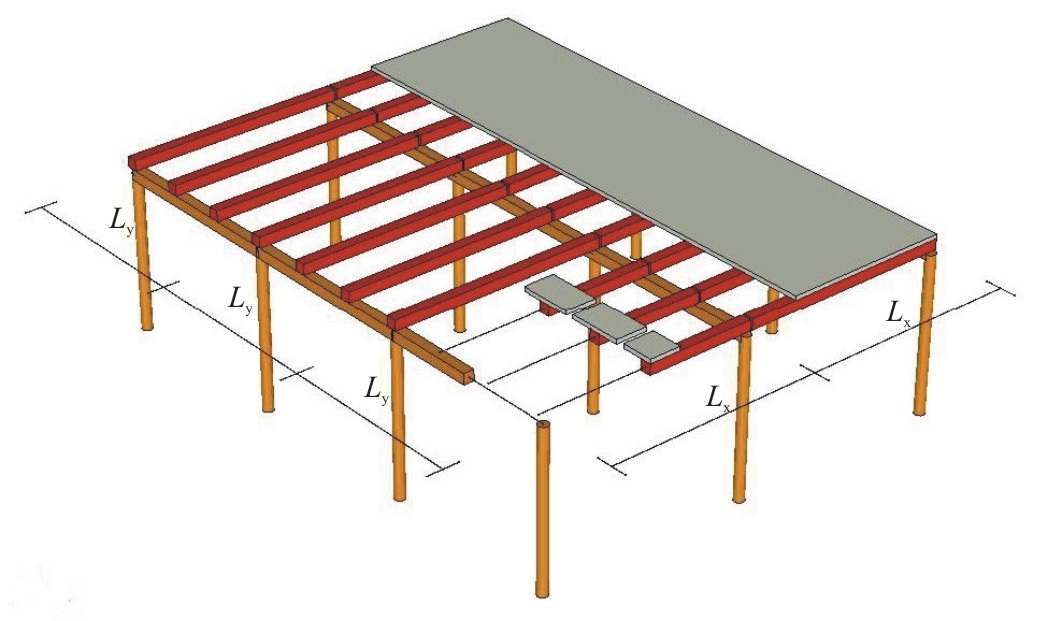
Gerendákon nyugvó kompozit lemezek rezgésvizsgálata (Kulcsár Bélával)
A lakóépületek gyakori szerkezetei a bordás lemezek, a kompozit lemezek és a fafödémek. Nagyobb támaszközök esetén az alkalmazás korlátja lehet a szerkezet alacsony sajátfrekvenciája, amely rontja a komfortérzetet. Ezeket a födémeket ortotrop (kompozit) lemezként lehet számítani. A szabadon feltámaszkodó ortotrop lemezek rezgésének számítására szolgáló, széleskörűen alkalmazott összefüggéseket az [5] monográfiában gyűjtöttük össze.

Sajnos ezek a képletek  gyakran túlbecsülik a födémek merevségét, elsősorban azért, mert nem veszik figyelembe a megtámasztó gerendák lehajlását. Ebben a kutatásban meg kívánjuk határozni a gerendákkal megtámasztott kompozit lemezek rezgésidejét, és az eredményeket kísérletekkel fogjuk verifikálni.

Gyakran alkalmaznak szálerősítéses műanyaggal (FRP-vel) erősített vasbeton oszlopokat, mivel a közrefogott beton szilárdsága jelentősen megnő és így az oszlop teherbírása is növekszik. Számos modell és kísérleti eredmény is található központosan nyomott oszlopokra, lényegesen kevesebb külpontos nyomás esetére. Ráadásul ez utóbbi esetben a publikált modellek jelentősen túlbecsülik a kísérletben kapott teherbírási eredményeket. Olyan modellt kívánunk kifejleszteni, amelyik megbízhatóan tudja számítani a külpontosan terhelt FRP-vel erősített vasbeton oszlopok teherbírását.

Módszerek

Az új rúdelmélet levezetéséhez a következő lépéseket fogjuk végrehajtani: először megoldjuk a rúd parciális differenciálegyenletét analitikusan oly módon, hogy a tengelyirányban trigonometrikus függvényt tételezünk fel. A megoldást végrehajtjuk mind az 1D (rúd) mind a 3D (héj) modellre. A helyettesítő merevségeket – a keresztmetszeti deformációkra tett apriori feltételezés nélkül –  határátmenet-képzéssel származtatjuk.

A lokális horpadásszámítás alapgondolata, hogy a rúdfalakat lemezekkel helyettesítjük, amelyeket a szomszédos falak rugalmasan megtámasztanak [2, 9]. A számítás kulcsa így a rugalmasan megtámasztott lemezek kritikus terhének meghatározása [8]. Ezek segítségével a lokális horpadás is számítható [9].

A kompozit födémek rezgésvizsgálatához összekapcsoljuk (i) a kompozit gerendák és ortotrop lemezek rezgésének eredményeit [5] és (ii) az összegzési tételeket. Az eredményeket kísérletekkel is verifikáljuk. Olyan egyszerű összefüggéseket vezetünk le, amelyek közvetlenül alkalmazhatók a tervezésben.

Numerikus modellt dolgozunk ki az FRP-vel erősített vasbeton oszlop vizsgálatára, amely a beton igen pontos, Papanikolaoutól és Kappos-tól származó modelljén alapul. Ezekkel várhatóan meg tudjuk magyarázni az irodalomban található furcsa jelenségeket [10]. Eredményeinket kísérletekkel is alátámasztjuk. 

Eddigi eredmények

Korábban levezettünk olyan rúdelméleteket [5, 6], amelyek képesek figyelembe venni az axiális-elcsavarodási és a hajlítási-elcsavarodási keresztmerevségeket. A síkbeli nyíráselméletet csavarásra általánosítottuk [5].
A kompozit rudak fokozottan érzékenyek a kihajlásra, és a hosszabb rudak a tengelyre merőleges teher hatására kifordulhatnak. Ezeket a problémákat megoldottuk  [1, 5].

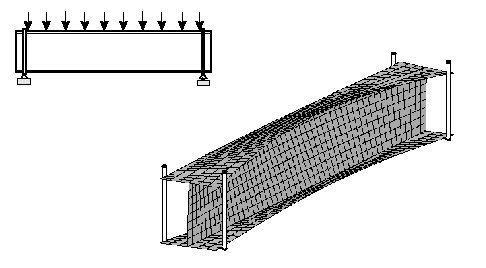
Ahogy írtuk, az axiálisan terhelt kompozit rudak egy fontos tönkremeneteli formája a lokális horpadás, egy dobozszelvény felső öve például az ábrán vázolt módon meghullámosodhat.

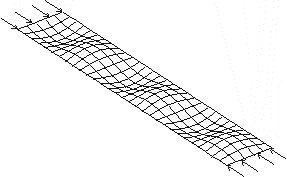
Ez alapvető kérdés a kompozit rudak tervezésél. Axiális nyomás és egyszerű hajlítás esetén ezt a problémát megoldottuk és publikáltuk [2, 5].

Rúdelméletek alkalmazásai

Sok esetben közvetlenül alkalmaznak rudakat (pl. repülőkben és épületekben), de még számos olyan terület van, ahol a rúdmodelleket lehet alkalmazni.

Sílécek és hódeszkák például kompozit szendvics-rúdként modellezhetők és így lehetővé válik ezek komplett dinamikai modellezése is. Ilyen módon jobb sporteszközöket lehet tervezni, és csökkenteni lehet a terepen végrehajtandó költséges kísérletek számát [4]. 
 
Magasházak földrengés-vizsgálatánál a házat egy konzolrúddal modellezhetjük [3], és ilyen módon igen egyszerűen meghatározhatjuk az épületre ható földrengésterheket.

Várható impakt, további kutatás

A levezetett rúdmodell lehetővé teszi, hogy kompozit rudakat pontosabban számoljunk, és így „jobb” (olcsóbb és biztonságosabb) szerkezeteket készítsünk. Ez éppúgy igaz lehet egy födémgerendára, mint egy szélturbina lapátjára, de akár egy golfütőre is.
A lokális horpadásvizsgálati és födémrezgés-eredmények olyan eszközt adnak a tervező kezébe, amellyel gyorsan és pontosan tud megbízható szerkezetet tervezni. Reményünk szerint az FRP-val erősített vasbeton oszlop vizsgálatára elkészített modellünk – egyedüliként – képes lesz megbízhatóan számítani ezeket a szerkezeteket.

Az eddig publikált eredményeink és hivatkozásaik megtalálhatók a KPA (MTMT) adatbázisban. A mérnöki gyakorlatban való fontossága miatt egyet emelünk ki: az axiálisan terhelt oszlopok lokális horpadásvizsgálatára levezetett összefüggéseinket mint legjobban használhatót javasolják alkalmazni, többek közt pl. L. Banks monográfiájában (Composites for Construction, Whiley, 2006).

Saját publikációk, hivatkozások, linkgyűjtemény

Résztvevők bemutatása:

Kollár László

Csuka Bernát

Pluzsik Anikó

Tarján Gabriella