 |
BMe Research Grant |

|
Doctoral School of Electrical & Electronic Engineering
BUTE, Dept. of Telecommunications, Laboratory of Acoustics
Supervisor: Dr. Fülöp Augusztinovicz, PhD.
Acoustical investigation of organ pipes by means of numerical techniques
Introducing the research area
 Scaling and tuning of organ
pipes are still performed according to the rules of thumb laid down in the
19th century. These rules lead to the desired sound characteristics
in most cases, however, in certain situations deviations from the traditional
mensuration are inevitable because of aesthetic or practical reasons. Then the
organ builder can only rely on his personal experience to achieve the
appropriate sounding.
Scaling and tuning of organ
pipes are still performed according to the rules of thumb laid down in the
19th century. These rules lead to the desired sound characteristics
in most cases, however, in certain situations deviations from the traditional
mensuration are inevitable because of aesthetic or practical reasons. Then the
organ builder can only rely on his personal experience to achieve the
appropriate sounding.
The objective of my research work – which is summarized briefly in the following – is the development and validation of a computer modeling toolkit, which is capable of calculating acoustical parameters of organ pipes and can provide a detailed picture of the sound generation mechanism. Model results aid the manufacturers in pipe mensuration and tuning, making the industrial processes of organ design, building and voicing more cost and time effective.
Note: additional research highlights, including audio and video material is
presented on the following webpage [link].
Brief introduction of the research place
The Laboratory of Acoustics performs research and development activities in
various fields of acoustics, such as vehicle and building acoustics, numerical
acoustics, sound recording technologies and audio signal processing methodology.
The laboratory has been involved in many international research and national
development projects and is actively participating in undergraduate and graduate
education. For a detailed information, see [link].
History and context of the research
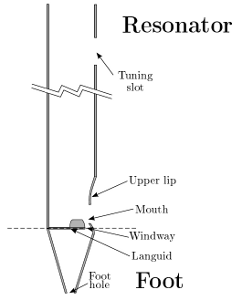 The sound generation
mechanism of organ pipes is a complicated physical process, since it includes
acoustical, fluid dynamical and mechanical phenomena inherently coupled [4, 6, 7]. In labial pipes, sound is produced as flowing air enters
the pipe through the foot hole. A thin jet of air emerges at the windway, which
hits the upper lip and produces the so-called edge tone [10]. The latter provides the excitation for the resonator.
Sound pressure waves reflected from the open or closed end of the resonator
modulate the air jet, forcing it into a periodic movement [20].
The sound generation
mechanism of organ pipes is a complicated physical process, since it includes
acoustical, fluid dynamical and mechanical phenomena inherently coupled [4, 6, 7]. In labial pipes, sound is produced as flowing air enters
the pipe through the foot hole. A thin jet of air emerges at the windway, which
hits the upper lip and produces the so-called edge tone [10]. The latter provides the excitation for the resonator.
Sound pressure waves reflected from the open or closed end of the resonator
modulate the air jet, forcing it into a periodic movement [20].
Most of the theoretical pipe models split this coupled system into
well-defined parts, separating the processes. In these models the pipe body is
represented by a simple, linear acoustic resonator [16, 22]. Attached to this part is the non-linear excitation, for
which several models have been developed [19, 23]. These models can predict certain parameters of the pipe
sound with sufficient accuracy, however, they do not provide any information on
some key characteristics such as transients [17] or the vibrations of pipe walls [18].
With the advances in computer techniques and the steep growth of the
available computational capacity, the importance of simulations based on
computational fluid dynamics keeps increasing [1, 12]. Nevertheless, the computational effort required for a
complete coupled simulation is still some orders of magnitude bigger than the
capacity at our disposal. Therefore, certain neglects and simplifications must
be made even in numerical models. The solution should be a
hybrid model, which could couple the parts of the system by the adequate
boundary conditions.
The research goal, open questions
In the first period of the research my task was to model organ pipe resonators by means of numerical acoustics, which included the development and comparison of modeling techniques. Self made implementation and validation of computational methods was also an objective. The questions to be answered included the maximum accuracy of resonant frequency prediction by numerical methods, or identifying cases where numerical models provide better results than analytical approximations. A further question was the predictions that could be made on the sound spectra from the transfer function of the resonator. Finally, the applicability of the results to the practice of organ design and pipe building was investigated, together with the optimization possibilities of pipe geometry based on the desired sound characteristics.
The INNOSOUND EU project (for detailed information, see link]) framed the first phase of the research. During the project I was given the opportunity to join in the work of the Musical Acoustic Group of the Fraunhofer Institute in Stuttgart for two short periods of time. In the project work, my aim and task was to develop a piece of software for organ builders, which allows them to easily access innovative design methods beside the traditional ones.
Moving on from the merely acoustical model, my objective in the second phase
of the research is the simulation of fluid dynamical phenomena in the sound
generation process. The questions to be answered are as follows. What kind of
simulation model and how much computational effort is required for the correct
simulation of the fluctuating air jet? Which acoustical analogy can be used to
reproduce the edge tone with sufficient accuracy? How is it possible to
incorporate the active interaction of acoustical and fluid flow effects into the
model?
Methodology
In the first phase of the research I examined organ pipes by means of a simplified acoustic resonator model. The simplest model of the pipe body is a cavity surrounded by perfectly rigid walls, which is coupled to the exterior acoustic field by two openings (the open end and the pipe mouth). Using this model the transfer function of the resonator can be calculated, which can amplify (or depress) some of the harmonic partials in the steady state sound. The transfer function is determined by the geometry of the resonator.
The main characteristic feature of the transfer function is that the higher number modes are not exactly coincident with the harmonics of the fundamental frequency but are slightly shifted upwards [17]. This phenomenon is called stretching. Decrease of quality factors of subsequent resonance peaks is also typical. Above the cut-off frequency the transfer function becomes irregular because of the excitation of transversal and combined modes.

Typical transfer function of a regular open pipe. Dotted blue lines denote the exact harmonics of the fundamental.
Dashed red line indicates the cut-off frequency.
There are a number of methods to solve the acoustical resonator
problem. In case of regular geometries, the problem can be solved analytically,
whereas irregular and more complex setups can be calculated using numerical
techniques. The coupling conditions, or the radiation impedances in other words,
that represent the connection between the interior and exterior fields play a
key role in the model.
I applied three different techniques for numerical acoustic modeling. Two of them were implemented by myself in Matlab environment. In the indirect boundary element method (IBEM) [5] the pipe is given by a surface mesh. Zero jump of pressure boundary conditions are imposed on the free edges of the geometry to ensure the continuity of the sound field. The coupled finite/boundary element method (FEM/BEM) [9] handles the resonator as an acoustic volume and invokes the direct boundary element method in order to determine the coupling impedances. By extending the finite element method by infinite elements (FEM/IEM) [2] the computational domain is expanded to a convex envelope circumscribing the pipe. Local boundary conditions are set up on this artificial exterior surface. Thus, the three methods are essentially different regarding boundary conditions, such as the properties of the resultant matrices describing the discretized systems of equations.
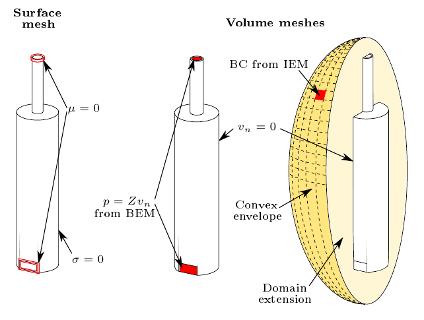
Mesh and boundary condition setup for numerical models: IBEM (left), FEM/BEM (middle), FEM/IEM(right).
Simulations were run on three different pipe types (open straight wooden
pipes, chimney flutes and open cylindrical pipes with tuning slots) with various
scaling parameters. Simulation results were compared with transfer function
measurements and then predictions were made on the steady state sound spectra,
which were verified by means of sound measurements.
In the second period of the research I work on the fluid dynamic
modeling of the excitation. The main challenge is the simulation of the free jet
and shear layer evolving near the windway and the lower lip. To validate the
model, two and three dimensional simulations were carried out and the results
were compared with measurement data published in [3].
Results
The modeling of radiation impedances was an important part of the resonator model development. I have shown how can the impedances be calculated by numerical methods and compared the results with analytical models [8, 11, 14], which gave a good agreement. It was also shown that, additionally to their frequency dependency, radiation impedances strongly depend on the spatial coordinates as well.
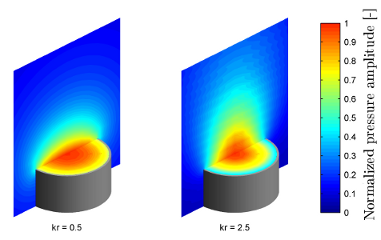
Radiation from the open end of an open cylindrical pipe.
At higher wave numbers (right hand side) the radiation is more directed.
I have shown that the FEM/BEM technique can be made faster by using interpolation and therefore, remarkable computational effort can be saved in the calculation of the coupling impedance matrix. However, none of the compared numerical methods proved to be significantly faster or more accurate than the other two. In the case of pipes with tuning slots I have shown that numerical methods give more accurate and reliable results than known analytical formulas (see [13]). Hence, it can be stated that the numerical simulations are especially advantageous in case of irregular geometries.

Comparison of simulated and measured transfer function in open pipe with tuning slot.
From my experiments performed on chimney flutes, I have found that it is possible to amplify certain harmonics in the steady state pipe sound with the adequate scaling of the resonator. The amplitude can increase by even 15-20 dB, which is clearly audible in the pipe sound. The main difficulty in scaling is that changing a single geometry parameter may modify all the modal frequencies at once. To overcome this problem, I have developed a scaling algorithm which is capable of determining the appropriate resonator dimensions given the desired fundamental frequency and the number of the harmonic to be amplified.
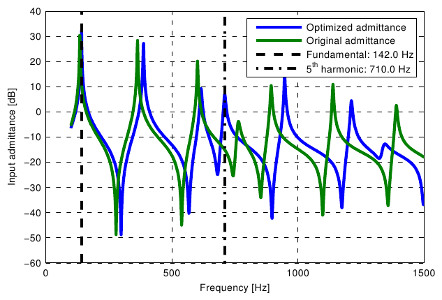
It is seen that one resonant frequency is tuned to the frequency of the fifth harmonic.
To round up the INNOSOUND project, I have developed the INNOScale mensuration
software, which not only includes traditional mensuration methods but offers direct access for the organ builder to innovative scaling techniques
that had been developed earlier in the project, such as narrower scaling for wooden pipe
stops. For the sake of convenience the software has a user-friendly interface
and flexible options.
Simulation results for the free jet responsible for the edge tone have been compared to measurements reported in [3]. It was found that the measured spreading of the jet was narrower than the prediction in our two-dimensional simulation. This is due to the fact that turbulent eddies can not fall apart along the third direction in the 2D case. 3D models gives a correct spreading, however, the cost of these simulations is much higher.
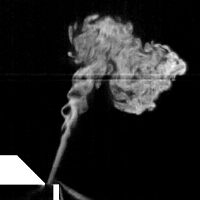
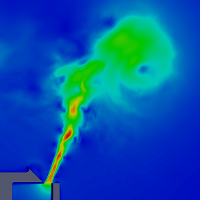
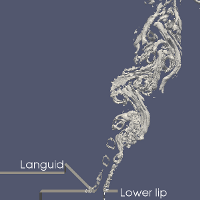
Air jet measurement and simulation. Left: flow visualization of the free jet, using LDA technique (source: [3]). Middle: Flow simulation of the same setup at approximately the same time instant. Right: 3D isosurface view of the turbulent coherent structures of the flow.
Expected impact and further research
The modeling toolkit and pipe design applications presented herein allow
organ builders to apply the newest results of organ sound research in everyday
practice directly. Measurements carried out on built pipe models validate the
applicability of the methods. Enhancing the modeling tools will presumable allow designers to predict further sound characteristics, which can only be obtained via measurements the present
day.
Plans on future research include the complete validation of free jet flow simulations and – based on these results – the aeroacoustic simulation of the edge tone generation. To verify the model, results presented in [3] serve as a guideline, among others. The final aim of the research is the development of a coupled acoustic - fluid flow model, which is capable of simulating transient effects in sound generation.
Acknowledgments
I would like to express my gratitude here to Dr. Judit Angster, Dr. Fülöp
Augusztinovicz, Dr. Máté Lohász and Dr. András Miklós. I should especially thank
Dr. Péter Fiala.
Publications, references, links
List of related publications:
Already published:
- P. Rucz, F. Augusztinovicz, P. Fiala. Determining the acoustic parameters of organ pipes by numerical techniques (in Hungarian). BUTE Thesis Students' Conference, 2009. (Conference paper in Hungarian.) [link]
- P. Rucz, F. Augusztinovicz, P. Fiala. Simulation of organ pipes' acoustic behavior by means of various numerical techniques. ICSV16 Conference, Kraków 2009. (Conference paper in English.) [link]
- P. Rucz. Determination of organ pipes' acoustic parameters by means of numerical techniques. Acoustic Review, Volume 10, Number 3-4, (2010) 39–47. (Journal paper in English.) [link]
- P. Rucz, J. Angster, F. Augusztinovicz, P. Fiala, A. Miklós, N. Manrique
Ortiz. Simulation of organ pipe transfer function by means of various
numerical techniques. ISMA2010 Conference, Leuven 2010. (Conference paper in
English.) [link]
Submitted:
- P. Rucz, F. Augusztinovicz, P. Fiala: Transfer function simulation of open
labial organ pipes. (Journal paper in English, submitted to Applied Acoustics,
2011.)
References
- S. Adachi. CFD analysis of air jet deflection – Comparison with Nolle’s measurements. in: Proceedings of the Stockholm Music Acoustics Conference, 2003, pp. 313–316.
- R. J. Astley. Infinite elements. in:
[15], pp. 199–230.
- H. Außerlechner, T. Trommer, J. Angster, A. Miklós. Experimental jet velocity and edge tone investigations on a foot model of an organ pipe. Journal of the Acoustical Society of America 126 (2) (2009) 878–886.
- J. W. Coltman. Sounding mechanism of the flute and organ pipe. Journal of the Acoustical Society of America 44 (4) (1968) 983–992.
- J. P. Coyette, J. Van de Peer. Acoustic Boundary Elements. in: [21], Ch. VII., pp. 1–32.
- S. A. Elder. On the mechanism of sound production in organ pipes. Journal of the Acoustical Society of America 54 (6) (1973) 1554–1564.
- N. H. Fletcher. Sound production by organ flue pipes Journal of the Acoustical Society of America 60 (1976) 1119–1132.
- N. H. Fletcher, T. D. Rossing. The physics of musical instruments. Springer, 1991.
- P. Göransson. Acoustic Finite Elements. in: [21], Ch. VI., pp. 1–45.
- D. K. Holger, T. A. Wilson, G. S. Beavers. Fluid mechanics of the edge tone. Journal of the Acoustical Society of America 62 (5) (1977) 1116–1128.
- F. Ingerslev, W. Frobenius. Some measurements of the end-corrections and acoustic spectra of cylindrical
open flue organ pipes. Transactions of the Danish Academy of Technical
Sciences (3) (1947) 1–42.
- H. Kühnelt. Simulating the sound generation in flutes and flue pipes with the Lattice-Boltzmann-Method. in: Proceedings of the International Symposium on Musical Acoustics, Nara, Japan, 2004, pp. 251–254.
- A. Lefebvre and G. P. Scavone. Refinements to the model of a single woodwind instrument tonehole. in: Proceedings of 20th International Symposium on Music Acoustics (Associated Meeting of the International Congress on Acoustics), Sydney and Katoomba, Australia, August 2010.
- H. Levine, J. Schwinger. On the radiation of sound from an unflanged circular pipe. Physical Review 73 (4) (1948) 383–406.
- S. Marburg, B. Nolte (Eds.). Computational Acoustics of Noise Propagation in Fluids – Finite and Boundary
element methods. Springer, 2008.
- M. E. McIntrye, R. T. Schumacher,
J. Woodhouse. On the oscillations of musical instruments. Journal of the
Acoustical Society of America 74 (5) (1983) 1325–1345.
- A. Miklós, A. and J. Angster. Properties of the sound of flue organ pipes. Acustica united with acta acoustica 86 (2000) 611–622.
- C. J. Nederveen, J.-P. Dalmont. Pitch and level changes in organ pipes due to wall resonances. Journal of
Sound and Vibration 271 (2004) 227–239.
- A. W. Nolle. Sinous instability of a planar air jet: Propagation parameters and acoustic excitation. Journal of the Acoustical Society of America 103 (1998) 3690–3705.
- G. Paál, J. Angster, W. Garen, A. Miklós. A combined LDA and flow-visualization study on flue organ pipes. Experiments in Fluids 40 (2006) 825–835.
- P. Sas (Ed.). Advanced Techniques in Applied and Numerical Acoustics. Katholieke Universitiet Leuven, 1997.
- M. P. Verge, A. Hirschberg, R. Caussé. Sound production in recorderlike instruments, II. A simulation model. Journal
of the Acoustical Society of America 101 (5) (1997) 2925–2939.
- S. Yoshikawa. Jet-wave amplification in organ pipes. Journal of the Acoustical Society of America 103 (5) (1998) 2706–2717.
Link collection:
Homepage of Péter
Rucz – research
