Villamosmérnöki Tudományok Doktori Iskola

BME VIK, Híradástechnikai Tanszék, Akusztikai Laboratórium

Témavezető: Dr. Augusztinovicz Fülöp, PhD.

Orgonasípok akusztikai vizsgálata numerikus technikákkal

A kutatási téma néhány soros bemutatása

Az orgonasípok méretezése és hangolása mindmáig a XIX. században lefektetett ökölszabályok alapján történik. E szabályok alkalmazásával legtöbbször megfelelő hangzás érhető el, viszont bizonyos esetekben a tradícionális menzúrától való eltérés - praktikus vagy esztétikai okokból - elengedhetetlen. Ekkor az orgonaépítő csak saját tapasztalataira támaszkodhat a kívánt hangzás beállításában.

A jelen pályázati anyagban röviden bemutatásra kerülő kutatómunkám célja olyan számítógépes modellezési apparátus fejlesztése és validációja, amely alkalmas orgonasípok akusztikai paramétereinek meghatározása, illetve, amelynek segítségével részletesebb képet kaphatunk a hangkeltési mechanizmusról. A modellezés eredményei segítik az orgonaépítőket a síptervezésben és -hangolásban, idő- és költséghatékonyabbá téve ezzel a tervezési, építési és behangolási folyamatokat.

Megjegyzés: a kutatáshoz kapcsolódó további anyagok - beleértve audio- és videoforrásokat - megtalálhatóak a [link] weboldalon.

A kutatóhely rövid bemutatása

A BME Híradástechnikai Tanszékének Akusztikai Laboratóriuma az akusztikán belül számos részterületen, elsősorban a jármű- és épületakusztika, numerikus akusztika, hangrögzítési és jelfeldolgozási technológiák területén végez kutató- és fejlesztőmunkát. A laboratórium munkatársai számos nemzetközi és hazai projekt mellett aktívan részt vesznek a tanszék oktatási tevékenységében. Bővebb információ: [link].

A kutatás történetének, tágabb kontextusának bemutatása

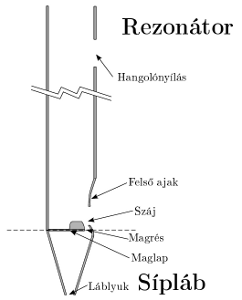Az orgonasípok hangkeltési mechanizmusa bonyolult fizikai folyamat, mivel csatolva jelennek meg benne áramlástani, akusztikai és mechanikai jelenségek [4, 6, 7]. Az ajaksípokat a síptestbe a síplábon keresztül beáramló levegő szólaltatja meg, mely a felső ajaknak ütközve létrehozza az ékhangot [10]. Utóbbi biztosítja a gerjesztést a rezonátor számára. A nyitott vagy zárt sípvégről reflektálódó hangnyomáshullámok a gerjesztő légnyelvet modulálják, így az periodikus mozgásba kezd [20].

Az elméleti sípmodellek ezt a csatolt rendszert jól definiált részegységekre bontva kezelik, szétválasztva ezzel az egyes jelenségeket. E modellekben a síptestet egyszerű lineáris akusztikai rezonátor helyettesíti [16, 22]. Ehhez kapcsolódik a nemlineáris gerjesztés, amelyre különböző leírások ismeretesek [19, 23]. Az említett modellekkel a síphang bizonyos paraméterei jól becsülhetőek, viszont egyes kulcsfontosságú jellemzőkről, pl. berezgési folyamatokról [17] vagy a sípfal rezgéseiről [18], nem kapunk információt.

A számítógépes technikák fejlődésével és a rendelkezésre álló számítási kapacitás rohamos növekedésével egyre inkább teret nyer a numerikus áramlástani szimuláció is [1, 12]. A teljes csatolt szimuláció számításigénye azonban még jelenleg is nagyságrendekkel túlmutat a rendelkezésre álló kapacitáson. Ezért a numerikus modellezés során is egyszerűsítésekkel, elhanyagolásokkal kell élnünk. A megoldást egy hibrid szimulációs módszer jelentheti, amely megfelelő peremfeltételekkel kapcsolja össze a rendszer egyes részeit.

A kutatás célja, a megválaszolandó kérdések.

A kutatás első szakaszának feladata ajaksípok numerikus akusztikai modellezése volt, ezen belül pedig analitikus és numerikus technikák fejlesztése és összehasonlítása. Célkitűzés volt a numerikus módszerek saját implementációja és validálása is. A megválaszolandó kérdések közé tartozott, hogy a numerikus technikák milyen pontossággal képesek becsülni a sípok rezonanciafrekvenciáit, illetve, hogy mely esetekben nyerhetünk az analitikus számításnál pontosabb eredményeket. Választ kerestünk arra, hogy a rezonátor átviteli függvénye alapján milyen következtetéseket vonhatunk le a síphangra vonatkozólag. Végül kérdés volt, hogy miként alkalmazhatók az eredmények a síptervezés gyakorlatában, vagyis hogyan lehetséges adott hangzáshoz optimalizálni a sípgeometriát.

A kutatás első felének az INNOSOUND (bővebb információ: [link]) európai uniós projekt adott keretet, melynek során kétszer is lehetőséget kaptam arra, hogy Stuttgartban rövidebb időre bekapcsolódhassak a Fraunhofer Intézet Zenei Akusztikai Csoportjának munkájába. A projektmunka során célom és feladatom volt egy olyan szoftver fejlesztése, amely az orgonaépítők számára könnyen elérhetővé teszi a tradícionális tervezési eljárások mellett az újonan fejlesztett metódusokat is.

A kutatás második szakaszában a pusztán akusztikai modelltől továbblépve, célom a hangkeltés áramlástani folyamatainak szimulációja. Az itt megválaszolandó kérdések: milyen áramlástani modell és mekkora számítási kapacitás szükséges a sípot megszólaltató légnyelv szimulációjához? Milyen akusztikai analógiával számítható kellő pontossággal az ékhang? Hogyan lehet az akusztikai és áramlástani modellek közötti aktív kapcsolatot létrehozni?

Módszerek

A kutatás első szakaszában az orgonasípokat egyszerűsített akusztikai rezonátormodellel vizsgáltam. A síptest legegyszerűbb modellje egy tökéletesen merev falakkal körülvett üreg, mely két nyílással (a síp nyitott vége és a száj) kapcsolódik a külső akusztikai térhez. A modell segítségével meghatározható a síptest átviteli függvénye, amely a stacionárius síphangban az egyes felharmonikusokat felerősítheti vagy éppen elnyomhatja. Az átviteli függvényt a rezonátor és a nyílások geometriája határozza meg.

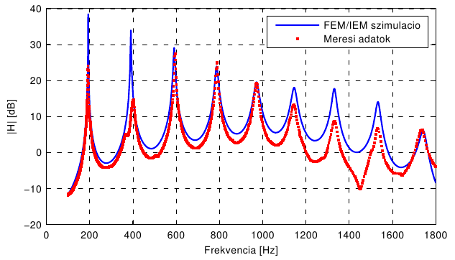
A rezonátor átviteli függvényének jellegzetessége, hogy a magasabb sorszámú módusok nem az alapfrekvencia egész számú többszöröseinél helyezkednek el, hanem a frekvenciáik felfelé tolódnak [17]. Ezt a jelenséget nevezzük nyúlásnak (stretching). Szintén jellegzetes, hogy az egymást követő rezonanciacsúcsok jósági tényezője egyre kisebb a frekvencia növekedtével. A vágási frekvencia felett az átviteli függvény a keresztirányú módusok miatt szabálytalanul ingadozóvá válik.

Szabályos, nyitott ajaksíp tipikus átviteli függvénye.
Kék pontozott vonalak: az alaphang felharmonikusai. Piros szaggatott vonal: a vágási frekvencia.

Az egyszerűsített akusztikai rezonátor probléma megoldására több módszer is ismeretes, és szabályos geometria esetén analitikus formulák is alkalmazhatóak a számításnál, míg bonyolultabb elrendezéseknél numerikus számításokat alkalmazhatunk. A modellben kulcsfontosságúak a külső és belső tér közti kapcsolatot megteremtő peremfeltételek, vagyis a sugárzási impedanciák.

Az akusztikai modellezéshez három különböző numerikus technikát alkalmaztam, melyek közül kettőt saját magam implementáltam Matlab környezetben. Az indirekt peremelem módszer (IBEM) [5] esetében a sípot felületi geometriával adjuk meg, a geometria szabad élein pedig zérus nyomásugrás peremfeltétel biztosítja a külső és a belső hangtér közötti folytonosságot. A csatolt perem-/végeselem (FEM/BEM) [9] módszer esetén a rezonátor térfogati hálóval adott, a csatoló impedanciákat pedig a direkt peremelem módszer alkalmazásával kapjuk meg. A végeselem módszert végtelen elemekkel kiegészítve (FEM/IEM) [2] a számítási tartományt kiterjesztjük a sípot körülvevő zárt konvex tartományra, majd ennek a tartománynak a határán állítunk fel lokális peremfeltételeket. A három modell tehát lényegesen eltér a peremfeltételek kezelésében, valamint a megoldandó egyenleteket leíró rendszermátrixok tulajdonságaiban.

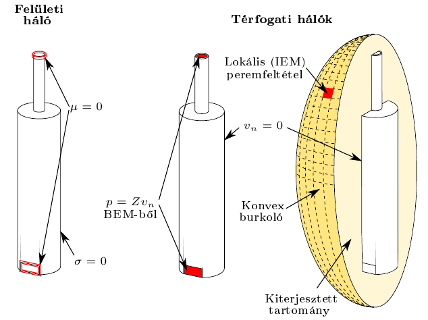
Numerikus modellek és a peremfeltételek megadása. Bal: IBEM, Közép: FEM/BEM, Jobb: FEM/IEM

A szimulációkat három különböző síptípuson (nyitott egyenes fasíp, csövesfuvola és hangolónyílással ellátott nyitott síp) futtattam, különböző geometriai paraméterekkel. A szimulációs eredményeket átviteli függvény-mérésekkel hasonlítottam össze, majd a modellből kapott eredmények alapján becsléseket készítettem a sípok stacionárius spektrumára, melyet mérésekkel validáltam.

A kutatás második szakaszában, az akusztikai modelltől továbblépve, a gerjesztés áramlástani modellezésével foglalkozom. A feladat fő nehézségét a magrésnél kilépő turbulens szabadsugár és nyíróréteg szimulációja jelenti. A validációhoz két- és háromdimenziós szimulációs eredményeket hasonlítottam össze mérési eredményekkel [3].

Eddigi eredmények

A rezonátormodellezés fontos részét képezte a sugárzási impedanciák szimulációja. Megmutattam, hogy az alkalmazott numerikus módszerekkel miként számíthatóak ezek az impedanciák, valamint összehasonlítottam ezeket az analitikus közelítéssel [8, 11, 14] és jó egyezést találtam. Megmutattam, hogy a sugárzási impedancia a frekvenciafüggés mellett erősen helyfüggő is.

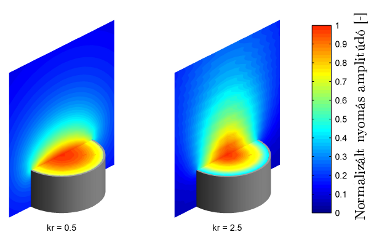
Hanglesugárzás nyitott sípvégről. Magasabb frekvenciák esetén (jobb oldali kép) a síp lesugárzása jobban irányított.

Megmutattam továbbá, hogy interpoláció alkalmazásával a FEM/BEM technika lényegesen felgyorsítható, így a csatolás számításakor jelentős számítási erőforrás takarítható meg. Az összehasonlított numerikus módszerek közül egyik sem bizonyult lényegesen hatékonyabbnak vagy pontosabban a másik kettőnél. A hangolónyílásos sípok esetében megmutattam, hogy az ismert analitikus közelítéseknél (lásd: [13]) pontosabb és megbízhatóbb eredményt kaphatunk numerikus technikák alkalmazásával. Ezzel megállapítást nyert, hogy a numerikus akusztikai szimuláció különösen előnyös irreguláris sípgeometriák esetén.

Hangolónyílással ellátott nyitott síp mért és szimulált átviteli függvényének öszehasonlítása.

Csövesfuvolákon végzett kísérletek alapján megállapítottam, hogy a rezonátor megfelelő méretezésével lehetőség van bizonyos felhangok kiemelésére a stacionárius síphangban. Az adott felhang relatív amplitúdója jó beállítás esetén akár 15-20dB-vel megnőhet, ami már jól hallható a síphangban. A méretezésben viszont nehézséget jelent, hogy egyetlen geometriai paraméter megváltoztatása az összes módus frekvenciáját módosítja. Ennek a nehézségnek a leküzdésére a fenti eredmények alapján kidolgoztam egy csövesfuvola méretező algoritmust, amely képes meghatározni a rezonátor méreteit a megadott alaphanghoz és a felerősíteni kívánt felharmonikus sorszámához.

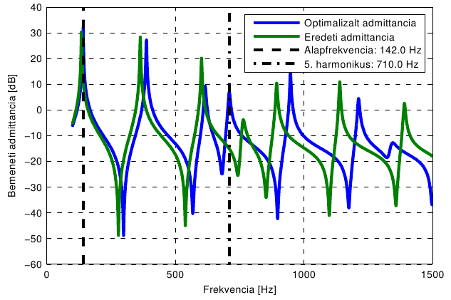
Csövesfuvola bemeneti admittanciájának optimalizálása.
Látható, hogy az egyik módust az 5. felharmonikus frekvenciájára hangoltuk.

Az INNOSOUND projekt lezárásaként kifejlesztettem az INNOScale nevű menzúráló szoftvert, amely tartalmazza a tradicionális menzúrálási eljárásokat, és ezek mellett lehetőséget kínál az orgonaépítőnek a projekt során kifejlesztett új méretezési eljárások közvetlen alkalmazására, például a szokottnál keskenyebb fasípregiszterek tervezésére. A szoftver felhasználóbarát kezelőfelülettel és flexibilis beállításokkal rendelkezik.

Az ékhangot keltő turbulens szabadsugár szimulációs eredményeit összevetettem a [3]-ban közölt eredményekkel. Megállapítható, hogy kétdimenziós szimuláció esetében - bár a módszer kvalitatíve jól modellezi a jelenséget - a kilépő sugár szétterjedése szélesebb, mint a mérésekben. Ennek oka, hogy a turbulens örvények a 2D esetben nem képesek szétesni a harmadik irányban. A 3D szimuláció esetében a szétterjedés szélessége jól egybeesik a mért eredményekkel, ez a szimuláció viszont jóval költségesebb a síkbeli modellnél.

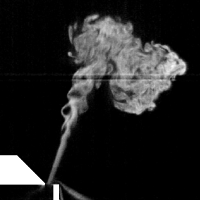
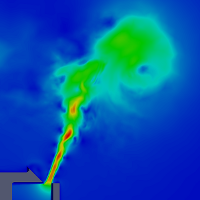
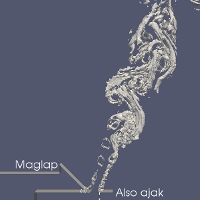
Légnyelv mérése és szimulációja. Bal: A légnyelv megjelenítése LDA méréssel, (forrás: [3]). Közép: áramlás-szimuláció azonos paraméterekkel. Jobb: A 3D turbulens koherens struktúrák megjelenítése a szimulációban.

Várható impakt, további kutatás

A bemutatott modellezési eszköztár és a síptervezést segítő alkalmazások olyan eszközöket adnak az orgonaépítők kezébe, amelyek segítségével a gyakorlatban is felhasználhatják az orgonahang-kutatás legújabb eredményeit. Az innovatív módszerek alkalmazhatóságát megépített sípokon elvégzett mérések validálják. Az apparátust továbbfejlesztve várhatóan lehetőség nyílik a tervezők számára olyan további jellemzők becslésére is, amelyek jelenleg csak mérésekkel ismerhetők meg.

A további kutatással kapcsolatos tervekhez tartozik a szabadsugár szimulációk teljes validációja, valamint ezeket folytatva az ékhang aeroakusztikai modellezése. E szimulációk ellenőrzéséhez – többek között – a [3]-ban közölt eredmények szolgálnak alapul. A kutatás végcélja a numerikus áramlástani és akusztikai szimuláció összekapcsolása, mellyel lehetőség nyílik például a hangkeltés tranziens folyamatainak modellezésére is.

Köszönetnyilvánítás

Ezúton is szeretném köszönetemet kifejezni Dr. Angster Juditnak, Dr. Augusztinovicz Fülöpnek, Dr. Lohász Máténak és Dr. Miklós Andrásnak. Külön köszönettel tartozom Dr. Fiala Péternek.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája. 

Kiadványban megjelent publikációk:

• P. Rucz, F. Augusztinovicz, P. Fiala, Orgonasípok akusztikai paramétereinek meghatározása numerikus technikákkal, BME Végzős konferencia, 2009. (Magyar nyelvű konferenciacikk) [link]
• P. Rucz, F. Augusztinovicz, P. Fiala, Simulation of organ pipes' acoustic behavior by means of various numerical techniques, ICSV16 Konferencia, Krakkó 2009. (Angol nyelvű konferenciacikk) [link]
• P. Rucz, Determination of organ pipes' acoustic parameters by means of numerical techniques, Akusztikai szemle, X. évfolyam, 3-4. szám, (2010) 39–47. (Angol nyelvű folyóiratcikk) [link]
• P. Rucz, J. Angster, F. Augusztinovicz, P. Fiala, A. Miklós, N. Manrique Ortiz, Simulation of organ pipe transfer function by means of various numerical techniques, ISMA2010 Konferencia, Leuven 2010. (Angol nyelvű konferenciacikk) [link]
  

Benyújtott publikációk:

• P. Rucz, F. Augusztinovicz, P. Fiala, Transfer function simulation of open labial organ pipes, (Angol nyelvű folyóiratcikk. Benyújtva az Applied Acoustics folyóirathoz, 2011.)
  

Hivatkozások listája.

1. S. Adachi, CFD analysis of air jet deflection – Comparison with Nolle’s  measurments, Megjelent: Proceedings of the Stockholm Music Acoustics Conference, 2003, 313–316.
2. R. J. Astley, Infinite elements, Megjelent: [15], 199–230.
   
3. H. Außerlechner, T. Trommer, J. Angster, A. Miklós, Experimental jet velocity and edge tone investigations on a foot model of an organ pipe, Journal of the Acoustical Society of America 126 (2) (2009) 878–886.
4. J. W. Coltman, Sounding mechanism of the flute and organ pipe, Journal of the Acoustical Society of America 44 (4) (1968) 983–992.
5. J. P. Coyette, J. Van de Peer, Acoustic Boundary Elements,Megjelent: [21], Ch. VII., 1–32.
6. S. A. Elder, On the mechanism of sound production in organ pipes, Journal of the Acoustical Society of America 54 (6) (1973) 1554–1564.
7. N. H. Fletcher, Sound production by organ flue pipes, Journal of the Acoustical Society of America 60 (1976) 1119–1132.
8. N. H. Fletcher, T. D. Rossing, The physics of musical instruments, Springer, 1991.
9. P. Göransson, Acoustic Finite Elements,Megjelent: [21], Ch. VI., 1–45.
10. D. K. Holger, T. A. Wilson, G. S. Beavers, Fluid mechanics of the edge tone, Journal of the Acoustical Society of America 62 (5) (1977) 1116–1128.
11. F. Ingerslev, W. Frobenius, Some measurements of the end-corrections and acoustic spectra of cylindrical open flue organ pipes, Transactions of the Danish Academy of Technical Sciences (3) (1947) 1–42.
    
12. H. Kühnelt, Simulating the sound genereation in flutes and flue pipes with the  Lattice-Boltzmann-Method, Megjelent: Proceedings of the International Symposium on Musical Acoustics, Nara, Japán, 2004, 251–254.
13. A. Lefebvre and G. P. Scavone. Refinements to the model of a single woodwind instrument tonehole, Megjelent: Proceedings of 20th International Symposium on Music Acoustics (Associated Meeting of the  International Congress on Acoustics), Sydney and Katoomba, Ausztrália, 2010. augusztus
14. H. Levine, J. Schwinger, On the radiation of sound from an unflanged circular pipe, Physical Review 73 (4) (1948) 383–406.
15. S. Marburg, B. Nolte (Szerk.), Computational Acoustics of Noise Propagation in Fluids – Finite and Boundary element methods, Springer, 2008.
    
16. M. E. McIntrye, R. T. Schumacher, J. Woodhouse, On the oscillations of musical instruments, Journal of the Acoustical Society of America 74 (5) (1983) 1325–1345.
    
17. A. Miklós, A. and J. Angster, Properties of the sound of flue organ pipes, Acustica united with acta acoustica 86 (2000) 611–622.
18. C. J. Nederveen, J.-P. Dalmont, Pitch and level changes in organ pipes due to wall resonances, Journal of Sound and Vibration 271 (2004) 227–239.
    
19. A. W. Nolle, Sinous instability of a planar air jet: Propagation parameters and acoustic excitation, Journal of the Acoustical Society of America 103 (1998) 3690–3705.
20. G. Paál, J. Angster, W. Garen, A. Miklós, A combined LDA and flow-visualization study on flue organ pipes, Experiments in Fluids 40 (2006) 825–835.
21. P. Sas (Szerk.), Advanced Techinques in Applied and Numerical Acoustics, Katholieke Universitiet Leuven, 1997.
22. M. P. Verge, A. Hirschberg, R. Caussé, Sound production in recorderlike instruments. II. A simulation model, Journal of the Acoustical Society of America 101 (5) (1997) 2925–2939.
    
23. S. Yoshikawa, Jet-wave amplification in organ pipes, Journal of the Acoustical Society of America 103 (5) (1998) 2706–2717.

Linkgyűjtemény.

Híradástechnikai Tanszék

Akusztikai Laboratórium

Áramlástan Tanszék

INNOSOUND (angol nyelven)

Rucz Péter honlapja - kutatás