 |
BMe Kutatói pályázat |

|
Csonka Pál Doktori Iskola
BME ÉPK, Szilárdságtani és Tartószerkezeti Tanszék
Témavezető: Dr. Domokos Gábor
Kavicsok morfológiája
A kutatási téma néhány soros bemutatása
 Milyen alakúak a
kavicsok? - erre az alapvető kérdésre keressük a választ a kutatás
során.
Milyen alakúak a
kavicsok? - erre az alapvető kérdésre keressük a választ a kutatás
során.
A természetben lépten-nyomon előforduló kavicsok változatos formavilága régóta fejtörést okoz a természettudósok számára. A kutatás alapötlete, hogy a statikai egyensúlyok fogalma egy természetes osztályozási rendszert kínál térbeli formák kódolására. Kutatómunkám egyrészt ezen új osztályozási rendszer elméleti vizsgálatát foglalja magában, másrészt annak feltérképezését, hogy a rendszer segítségével hogyan és milyen mélységben kódolható a kavicsok morfológiája és kopási folyamata.
A kutatóhely rövid bemutatása
A Szilárdságtani és Tartószerkezeti
Tanszék mechanikai és szerkezettervezési problémák széles körével
foglalkozik. A kutatási
témák nemcsak acél-, fa-, falazott, kompozit,
ponyva-, vasbeton- és vályogszerkezetekkel, hanem stabilitásvesztési
problémákkal és földrengési méretezéssel is kapcsolatosak. Kutatási tevékenységünk a
mechanika és az alkalmazott matematika számos területére kiterjed, a kavicsok
alakja és kopási folyamatai mellett oktatóink foglalkoznak például aszteroidák
alakdinamikájával, ütközéseknek kitett merev testek stabilitási kérdéseivel és
populációdinamikával is.
A kutatás történetének, tágabb kontextusának bemutatása
A kavicsok geometriája iránt Arisztotelész [5] óta neves tudósok sora érdeklődött [6][7]. A téma ma is az érdeklődés középpontjában áll [8][9][10], hiszen a természetben található, eróziós folyamatok által létrehozott formák (legyen szó akár domborzati formákról, akár kavicsokról) vizsgálata maguknak az eróziós folyamatoknak a megértésében segít. A kavicsok alakja információt hordoz az üledékképződés, -szállítás, -lerakódás körülményeiről [11][12], ezáltal segít a fáciesek elkülönítésében.
A geológusok számos alak-indexet és ezekre épülő osztályozási rendszert
javasoltak a kavicsok morfológiájának leírására [12][13][14][15]. Jelenleg is élénk vita tárgyát képezi, hogy ezek közül melyik a leginformatívabb rendszer [16][17]. Ezek a klasszikus rendszerek hosszméréseken
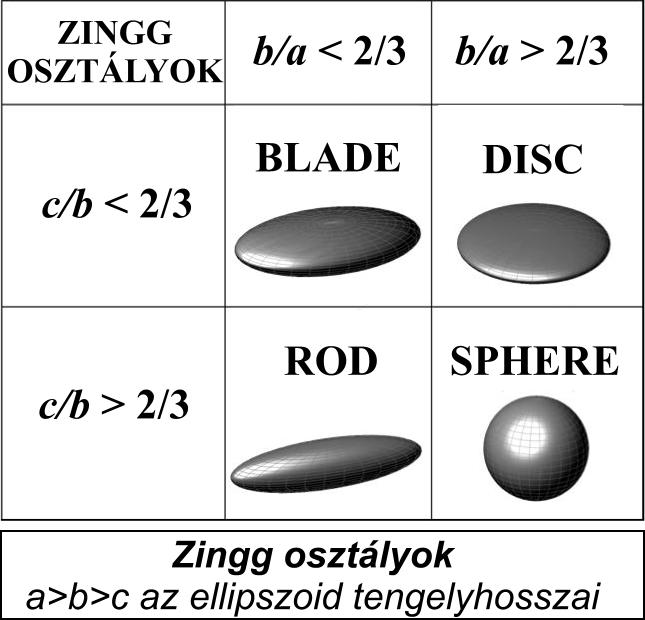
alapulnak, közülük a legelterjedtebb az ún. Zingg-osztályozás [15], amely a kavicsok alakját háromtengelyű ellipszoiddal
közelíti, s a tengelyarányok alapján négy osztályba sorolja a formákat. A
klasszikus alak-osztályozási rendszerek kétségkívül hasznosnak bizonyultak a
gyakorlatban, ám a hosszmérések miatt több, a mérő személy által megbecsült
önkényes adatot is tartalmaznak.
A kutatás célja, a megválaszolandó kérdések
A kutatás fő célkitűzése egy olyan új osztályozási rendszer felállítása a kavicsok morfológiájára, amely egyrészt elkerüli a hosszméréseken alapuló osztályozási rendszerekben rejlő bizonytalanságokat, másrészt a gyakorlatban könnyen alkalmazható a geológusok számára. Az új osztályozás a statikai egyensúlyok fogalmára támaszkodik, és ezek száma, típusa, eloszlása, s az egyensúlyok közötti kapcsolatok alapján kódolja a térbeli formákat.

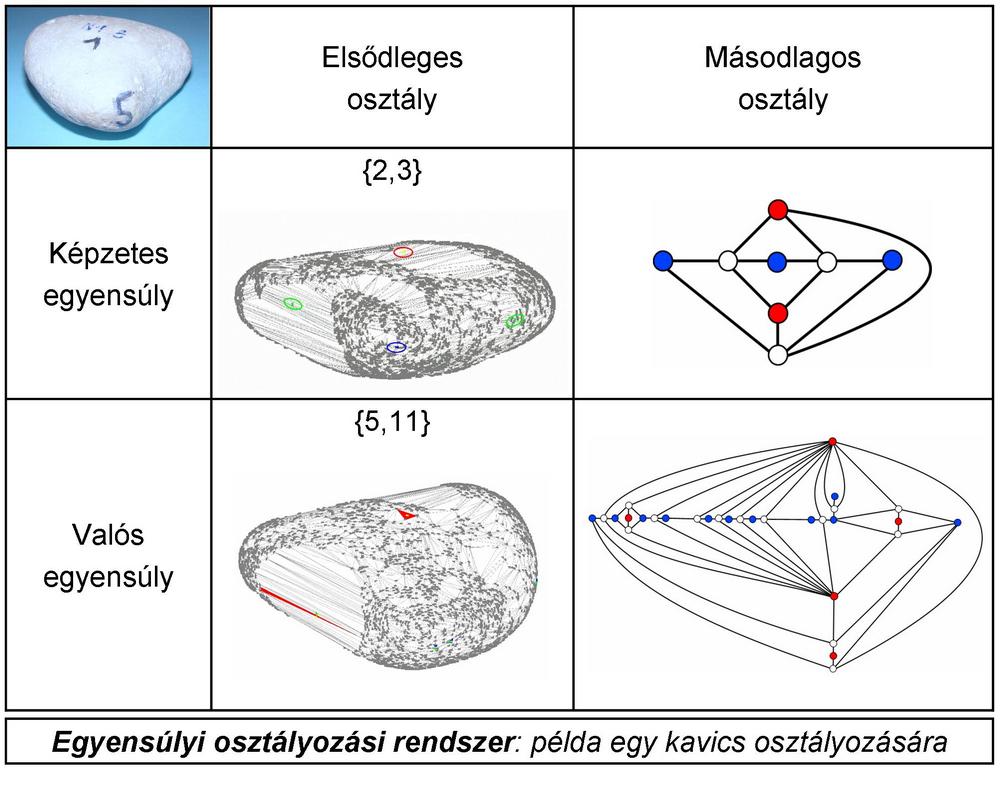
A kód alapja a stabil és instabil egyensúlyi helyzetek száma, mely alapján minden homogén, konvex test egyértelműen osztályba sorolható [18], ezt nevezzük elsődleges osztályozásnak. A kocka elsődleges osztálya például a {6,8} osztály, mert mind a 6 lapján van egy stabil egyensúly és mind a 8 csúcsa egy instabil egyensúly. Domokos Gábor és Várkonyi Péter találmánya, a Gömböc [19] az {1,1} osztályba tartozik (mono-monostatikus test).
A morfológia ennél részletesebb leírását kapjuk, ha azt is megvizsgáljuk, hogy mely egyensúlyi pontok szomszédosak egymással. Ezek a szomszédsági viszonyok a kavics felületén egy gráffal írhatóak le, ez a gráf a másodlagos osztályozás alapja.
A fenti osztályozási rendszert érdemes még tovább bővíteni a képzetes egyensúlyok fogalmával. „Nagyítón keresztül” nézve a kavicsok felszínén számos mikroszkopikus méretű egyensúlyt találunk, ezek a kavics valós egyensúlyai. A külső szemlélő szabad szemmel nem képes megkülönböztetni ezeket a valós egyensúlyokat, mert azok csoportokban (falkákban) helyezkednek el a kavics felszínén [3][4]. Helyette a kísérletező magukat a falkákat észleli egy-egy képzetes egyensúlyként.
A kutatás magában foglalja a fent leírt osztályozási rendszer, az elsődleges, másodlagos osztályozás, valós és képzetes egyensúlyok elméleti megalapozását, az osztályozás kavicsokon történő gyakorlati megvalósítását, és az ebből kinyerhető morfológiai információk feltérképezését.
A kutatás másik fő célkitűzése az eróziós folyamatok, ezen belül elsősorban
kavicsok kopási folyamatainak megértése és modellezése, különös tekintettel a
fent leírt új osztályozási rendszerre. Az új rendszer előnye, hogy csak
természetes számokat használ, így minden térbeli formához egyértelműen
hozzárendelhető egy kód, és e kód változása a megfelelő technikai és matematikai
eszközökkel nyomon követhető, ha egy adott kopási folyamat során a test kódját
rendszeres időközönként előállítjuk. Célunk annak megértése, hogy egy így
előállítható kódsorozattal hogyan követhető le a morfológia változása, és a
különböző kopási folyamatokhoz milyen kódsorozat rendelhető.
Módszerek
 A képzetes
egyensúlyok megszámlálása egyszerű és gyors kézi kísérletekkel
elvégezhető kavicsokon. 3D testek felszínén tipikusan 3 fajta egyensúlyt
találunk: stabil egyensúlyt, instabil egyensúlyt, illetve nyeregpontot, ezek számát
rendre jelölje S, U, illetve H. A Poincare-Hopf
tétel [20] alapján gömb topológiájú testekre S+U-H=2, így
elegendő a kavics stabil és instabil egyensúlyainak megszámlálása; a
nyeregpontok száma ebből már adódik. A kézi kísérlet alapján megadható a kavics
képzetes egyensúlyai által meghatározott elsődleges osztály:
{S,U}.
A képzetes
egyensúlyok megszámlálása egyszerű és gyors kézi kísérletekkel
elvégezhető kavicsokon. 3D testek felszínén tipikusan 3 fajta egyensúlyt
találunk: stabil egyensúlyt, instabil egyensúlyt, illetve nyeregpontot, ezek számát
rendre jelölje S, U, illetve H. A Poincare-Hopf
tétel [20] alapján gömb topológiájú testekre S+U-H=2, így
elegendő a kavics stabil és instabil egyensúlyainak megszámlálása; a
nyeregpontok száma ebből már adódik. A kézi kísérlet alapján megadható a kavics
képzetes egyensúlyai által meghatározott elsődleges osztály:
{S,U}.
 A valós
egyensúlyok azonosítása kavicsokon már munkaigényesebb feladat, ellenben az
ebből kinyerhető információ is jóval részletesebb. A mikroszkopikus léptékben
megjelenő valós egyensúlyok detektálása korszerű 3D
szkenneléssel lehetséges. A 0,1 mm pontosságú szkennelést egy CNC gépbe
fogatott 3D lézer-szkennerrel végeztük a BME
Gyártástudomány és -technológia Tanszékével együttműködve. A szkennelés
eredménye egy igen sűrű, háromszögelt poliéderháló, melyen az egyensúlyi pontok
számítógép segítségével azonosíthatók.
A valós
egyensúlyok azonosítása kavicsokon már munkaigényesebb feladat, ellenben az
ebből kinyerhető információ is jóval részletesebb. A mikroszkopikus léptékben
megjelenő valós egyensúlyok detektálása korszerű 3D
szkenneléssel lehetséges. A 0,1 mm pontosságú szkennelést egy CNC gépbe
fogatott 3D lézer-szkennerrel végeztük a BME
Gyártástudomány és -technológia Tanszékével együttműködve. A szkennelés
eredménye egy igen sűrű, háromszögelt poliéderháló, melyen az egyensúlyi pontok
számítógép segítségével azonosíthatók.
A másodlagos osztályt az egyensúlyi pontok közötti heteroklinikus
pályák alkotta ún. Morse–Smale-komplex [21] topológiája határozza meg; ez egy síkba rajzolt gráffal
szemléltethető, amelynek csúcsai az egyensúlyi pontok, az élek pedig azt
reprezentálják, hogy mely egyensúlyi pontok szomszédosak a kavics felületén. A
valós egyensúlyok alkotta gráf egy ismert algoritmussal [21] addig egyszerűsíthető, míg a mikroszkopikus léptékű valós
egyensúlyok eltűnnek, és csak a makroszkopikus léptékű, a kézi kísérletek során
érzékelhető egyensúlyok maradnak hátra – ez a képzetes egyensúlyok alkotta gráf.
Geometriailag ez a gráf-egyszerűsítő algoritmus annak feleltethető meg, hogy a
poliéder felületet „kisimítjuk”.
Eddigi eredmények
A kézi kísérletek előnye, hogy a képzetes egyensúlyok száma igen gyorsan és egyszerűen, akár terepi körülmények között is megszámlálható, így az új módszer hasznos eszközzé válhat a geológusok kezében. Egyszerűsége ellenére ez a kód meglepően jól jellemzi a kavicsok geometriáját, ugyanis szoros kapcsolat mutatható ki a Zingg-osztályok és az elsődleges képzetes egyensúlyi osztályok között. Mintegy 1000 kavics osztályozása alapján azt találtuk, hogy az egyensúlyi osztályozás egyszerűsített változata 80-90%-os pontossággal tartalmazza mindazokat az információkat, amit a Zingg-osztályozás [1][2], ugyanakkor az új rendszer ennél pontosabb képet nyújt a morfológiáról. Az elsődleges osztályozás például jól jellemzi a koptatottságot, mert világos különbséget tesz pl. egy gömb, egy tetraéder és egy kocka között, míg a klasszikus, hosszméréseken alapuló rendszerekben, így például a Zingg-rendszerben ezek a formák egyazon osztályba esnek. Az új rendszer különösen alkalmas poliéderek osztályozására, így például kristályalakok új szemléletű rendszerezésére [2].
A fentebb bemutatott 3D szkenneléses módszerrel kimutattuk, hogy a valós egyensúlyok a kavicsok felszínén csoportokban (falkákban) helyezkednek el; egy-egy ilyen falkát a kézi kísérletek során egy-egy képzetes egyensúlyként azonosít a kísérletező. A valós és képzetes egyensúlyok (a mikro- és makroszkopikus egyensúlyok) skálája a gömbhöz közeli kavicsok kivételével jól szétválik [3], így a kézi kísérletek megbízhatóak, a kísérletező nagy biztonsággal el tudja dönteni, hogy a kavicsnak hány (képzetes) stabil, illetve instabil egyensúlyi pontja van.
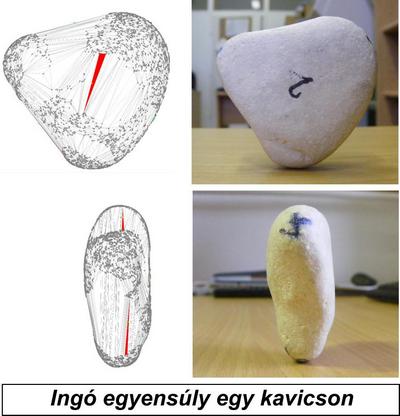 A valós és
képzetes egyensúlyok fogalmával szemléletesen magyarázható egy igen érdekes
jelenség: az ingókövek látványos
egyensúlyi pozíciója. Ezek olyan hatalmas kőtömbök, amelyek az intuíciónak
ellentmondó egyensúlyi helyzetben állnak, és nagy tömegük ellenére a legkisebb
erőhatásra is mozogni, inogni kezdenek. Szokatlan viselkedésük miatt a múltban
számos hiedelem kötődött az ingókövekhez, kapcsolatba hozták például azokat a
boszorkánysággal is. Hasonló, de kisebb léptékű alkotásokat mesterségesen is létrehoznak „kőegyensúlyozó-művészek”.
A jelenség magyarázatára egy új fogalmat, az ingó egyensúly fogalmát
vezettük be [3]: az ingó egyensúly olyan stabil valós egyensúly, amely egy
instabil képzetes egyensúlyhoz tartozik. Ez a fogalom világosan magyarázza annak az érzésünknek, hogy ellentmond az intuíciónak az ingókövek egyensúlyi helyzete: a
mikroszkopikus léptékű stabil valós egyensúlyt a külső szemlélő nem látja, csak
azt érzékeli, hogy makroszkopikus léptékben egy instabil helyzetről van szó.
A valós és
képzetes egyensúlyok fogalmával szemléletesen magyarázható egy igen érdekes
jelenség: az ingókövek látványos
egyensúlyi pozíciója. Ezek olyan hatalmas kőtömbök, amelyek az intuíciónak
ellentmondó egyensúlyi helyzetben állnak, és nagy tömegük ellenére a legkisebb
erőhatásra is mozogni, inogni kezdenek. Szokatlan viselkedésük miatt a múltban
számos hiedelem kötődött az ingókövekhez, kapcsolatba hozták például azokat a
boszorkánysággal is. Hasonló, de kisebb léptékű alkotásokat mesterségesen is létrehoznak „kőegyensúlyozó-művészek”.
A jelenség magyarázatára egy új fogalmat, az ingó egyensúly fogalmát
vezettük be [3]: az ingó egyensúly olyan stabil valós egyensúly, amely egy
instabil képzetes egyensúlyhoz tartozik. Ez a fogalom világosan magyarázza annak az érzésünknek, hogy ellentmond az intuíciónak az ingókövek egyensúlyi helyzete: a
mikroszkopikus léptékű stabil valós egyensúlyt a külső szemlélő nem látja, csak
azt érzékeli, hogy makroszkopikus léptékben egy instabil helyzetről van szó.
Várható impakt, további kutatás
A további kutatás során célzott terepi mérések mellett geológiai szempontból
érdekes helyszíneken kavicsminták begyűjtését tervezzük. A mintagyűjtés
alkalmas helyszíneinek megválasztásával lehetővé válik a különböző
üledékképződési, -szállítási, -lerakódási környezetek vizsgálata és
elválasztása, a kavicsok kopási folyamatának nyomon követése. Ezzel párhuzamosan
a kopási folyamat laborkísérletek útján, illetve numerikus és analitikus modellek
segítségével is vizsgálható. Végső célunk a különböző kopási folyamatok
megértése és modellezése, különös tekintettel a fent leírt osztályozási
rendszerre.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája:
[1] G. Domokos, A. Sipos, T. Szabó, P. Várkonyi (2010), Pebbles, Shapes, and Equilibria, Mathematical Geosciences, Vol 42, 29–47.
[2] T. Szabó, G. Domokos (2010), A new classification system for pebble and crystal shapes based on static equilibrium points,Central European Geology, Vol 53/1, 1–19.
[3] G. Domokos, A. Sipos, T. Szabó, The mechanics of rocking stones: equilibria on separated scales, Benyújtva: Mathematical Geosciences. Kézirat
[4] G. Domokos, Zs. Lángi, T. Szabó, On the equilibria of finely discretized curves and surfaces, Benyújtva: Monatshefte für Mathematik. Kézirat
Linkgyűjtemény:
BME Szilárdságtani és Tartószerkezeti Tanszék
Az ingókövekről:
Youtube: Bill Dan
"kőegyensúlyozó-művész"
Hivatkozások listája:
[5] Aristotle, in Minor Works, Mechanical Problems, Question 15, translated by W. S. Hett (Harvard University, Cambridge, MA, 2000)
[6] Lord Rayleigh (1942), Pebbles, natural and artificial, Proc. Roy. Soc. London A, 182. kötet, 107–118.
[7] F.J. Bloore (1977), The shape of pebbles, Mathematical Geology,
9. kötet, 113-122.
[8] W. Ashcroft (1990), Beach pebbles explained, Nature, 346. kötet,
227. oldal
[9] M. Lorang, P.D. Komar (1990), Pebble Shape, Nature, 347. kötet,
433–434.
[10] T. Yazawa (1990), More pebbles, Nature, 348. kötet, 398. oldal
[11] D.J. Graham, N.G. Midgley (2000), Graphical representation of particle shape using triangular diagrams: an Excel spreadsheat method, Earth Surface Processes and Landforms, 25. kötet, 1473–1477.
[12] E. Sneed, R.L. Folk (1958), Pebbles in the lower Colorado River, Texas, a study in particle morphogenesis, J Geology, 66. kötet, 114–150.
[13] W.C. Krumbein (1941), Measurement and geologic significance of shape and
roundness of sedimentary particles, J Sed Petr, 11. kötet, 64–72.
[14] C.K.
Wentworth (1922), The shapes of beach pebbles, US Geological Survey Professional
Paper, 131-C. kötet, 75–83.
[15] T. Zingg (1935), Beitrag zur Schotteranalyse, Schweizer Miner, Petrog. Mitt., 15. kötet, 39–140.
[16] W. Illenberger (1991), Pebble shape (and size!), J. of Sedimentary
Research, 61. kötet, 756.
[17] S.J. Bott, K. Pye (2008), Particle shape: a
review and new methods of characterization and classification, Sedimentology
55. kötet, 31–63.
[18] P. Várkonyi, G. Domokos (2006), Static equilibria of rigid bodies: dice, pebbles and the Poincaré-Hopf Theorem, J Nonlinear Sci, 16. kötet, 255–-281.
[19] P. Várkonyi, G. Domokos (2006), Mono-monostatic bodies: the answer to Arnold’s question, The Mathematical Intelligencer 28. kötet, 34–38.
[20] V.I. Arnold (1998), Ordinary differential equations, 10th printing, MIT Press, Cambridge
[21] H. Edelsbrunner, J. Harer, A. Zomorodian (2003), Hierarchical Morse-Smale complexes for piecwise linear 2-manifolds, Discrete Comput Geom 30. kötet, 87–107.
