Doctoral School of Mathematics and Computer Science

Department of Computer Science and Information Theory

Supervisor: Dr. Gábor Simonyi

Graph colouring problems

Introducing the research area

The topic of my PhD research is graph theory, more closely various problems on graph coloring. I investigate the asymptotic behaviour of graph parameters related to colouring, and also covering problems associated with edge colouring.

My PhD supervisor is Gábor Simonyi, a professor of BUTE Department of Computer Science and Information Theory and a research fellow of the Alfréd Rényi Institute of Mathematics.

Brief introduction of the research place

I carry out my research work at BUTE Department of Computer Science and Information Theory. The main research topics of our department include the matroid theory, complexity theory (parametrized complexity, efficiency of quantum computing), reliability of communication networks, VLSI  routing and declarative programming. Many of us are doing research on combinatorics and graph theory, for example on questions on Hamiltonian cycles or on crossing numbers.

History and context of the research Graph theory is an important branch of mathematics, more precisely of combinatorics. Its main concept is the graph, which consists of a collection of vertices and of edges that pairwise connect vertices. Such structures play an important role in various areas of life. Graphs can be used to represent social or communication networks, structure of molecules, computing processes. Moreover, the theory of these structures is often an essential tool to the solution of questions in several fields. The chromatic number of a graph is the minimum number of colours which can be assigned to the vertices such that no two adjacent vertices share the same colour. This is one of the most intensively investigated graph parameters, and its behaviour is only understood is some situations, but is totally unknown in most of the cases. One of main applications of colouring is the scheduling theory. (In a very basic example, the vertices of the graph represent the computer tasks to schedule, and the edges correspond those pairs  which are required to run on different machines. In this case the minimum number of machines in a proper scheduling is the chromatic number of the associated graph.) The popular puzzle, the Sudoku can also be formulated as a colouring problem of a special graph.

Graph of a biological network (source).

An optimal colouring of the five-wheel; the chromatic number of this graph is 4.

In my PhD research I concentrate on two larger topics of graph colouring problems: the asymptotic behaviour of graph parameters for different graph powers and various covering problems of edge-coloured graphs. I started working on graph colouring problems in the frame of Students' Scholarly Circles, as a third year undergraduate. I also prepared my master thesis in this topic, which I continued since 2008 as a PhD student. For my bachelor thesis as a computer engineering student  I am developing softwares which help my research in graph colouring problems.

The research goal, open questions

Asymptotic values of graph parameters for graph powers

Several graph parameters show an interesting behaviour when they are investigated for different powers of graphs.  One of the most famous examples of such behaviour is that of the Shannon capacity of graph [Shannon], which is the theoretical upper limit of channel capacity for error-free coding in information theory. This concept can be derived in the following way.

Let us consider a channel on which one can transmit five characters. Because of the noise in the channel some pairs or characters may be confused  during the transmission. The graph on the figure represents the channel: the vertices are the characters, and two vertices are connected with en edge if they can be confused. (By sending a character 'k' the receiver may get 'h' or 'b'  in stead of 'k', but he cannot receive 'n' or 'p'.) It is easy to see that to realize a decodable, error-free coding (in a simple case) we should choose pairwise distinguishable characters. So we can use at most two characters, as there are no more characters without an edge between them.

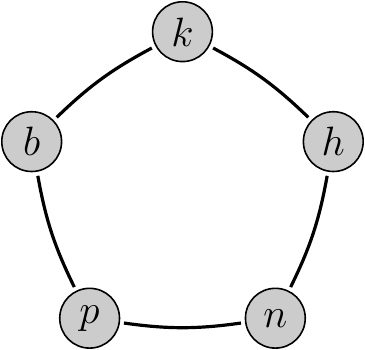The graph of a simple channel, a pentagon.

An independent set of the second power of the pentagon for normal product.

If we transmit more characters together on the channel, then we can increase the information rate (in units of information per unit time). The following five character pairs are pairwise distinguishable:  'kk', 'hn', 'nb', 'ph', 'bp', since any two of them are distinguishable in the first or in the second element.  Combining these pairs using  characters we can transmit different messages as well. It was an open problem for a long time whether or not this is the optimum, and a celebrated result of Lovász is that the Shannon-capacity of the pentagon is , that is, one can not send more then distinguishable messages with characters [Lovász].

Shannon-capacity of a graph is defined as the normalized limit of the independence number under the so-called normal power. The independence number of a graph is the size of the largest independent set where an independent set is a subset of the vertex set which contains no edge. The normal product of graphs is defined on set of pairs formed by the vertex set of the two base graphs, and we connect two pairs if the corresponding elements are equal or form an edge in both coordinates. (This product describes the confusability relation of messages written above.)

We consider similar questions in [1], [2], [3], [5], where we investigate the asymptotic behaviour of colouring-related graph parameters for different graph powers in the articles.

Covering problems of edge-coloured graphs

In my PhD studies I also investigated covering problems of edge-coloured graphs. Probably the most famous open question in this area is the Ryser conjecture (appeared in the Thesis of his student, Henderson [Henderson]). An interesting special case of the conjecture states that if one colours the edges of a complete graph with colours, then the vertex set can be covered by the vertices of at most monochromatic connected components [Gyárfás].

Covering with components is easy, as choosing a vertex as a centre, the corresponding stars in different colours cover the whole vertex set of graph. The conjecture states that one less component is also enough in any case.

Left: An edge-colouring of the complete graph on seven vertices with four colours. Middle: Covering with four stars.
Right: Covering with just one monochromatic connected component.

In the works [4], [6], [7] we prove results on covering problems of edge-colored graphs.

Methodology and results

Asymptotic values of graph parameters for graph powers

The Hall-ratio of a graph is the fraction of the number of vertices and the independence number maximized over all subgraphs of the graph. (For example, in the case of the five-wheel shown above, the value of this parameter is 3). The introduction of this concept was motivated by colouring problems [Cropper et al]. Simonyi investigated the asymptotic value of this graph parameter for different graph powers. He showed that for normal power  the asymptotic value is the Witsenhausen-rate, while for co-normal power we obtain the fractional chromatic number as the limit of the sequence [Simonyi]. The Witsenhausen-rate is defined as the normalized asymptotic value of the chromatic number, and it also plays role in information theory.

The fractional chromatic number is the fractional relaxation of the chromatic number. This means that we put real weights on the independent sets of the graph, such that  for every vertex the sum of the weights corresponding to those independent sets which contain that vertex is at least 1, and with this condition we  want to minimise the total weight put on all independent sets of the graph. The value of this minimum is the fractional chromatic number of the graph. (In a proper colouring of a graph, the vertices coloured with the same colour form an independent set, thus this concept is a generalization of the chromatic number concept. If we only consider integer values (0 or 1) in the definition, then  we get back the concept of chromatic numbers.)

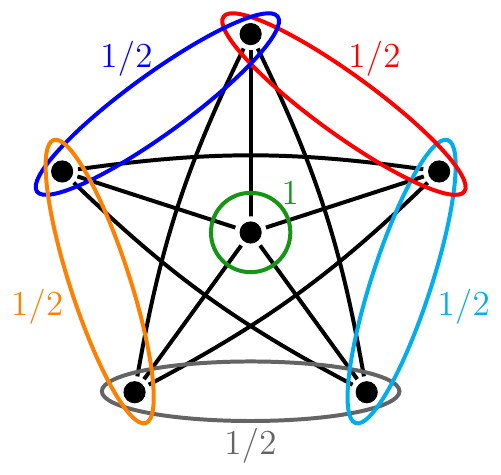An optimal fractional coloring of the five-wheel, the fractional chromatic number of the graph is 3,5.

In my master thesis I proved the conjecture of Simonyi stating that the fractional chromatic number is the asymptotic value for lexicographic power, too [1]. The analog question for the direct power is different from the previous ones in many aspects, and its confirmation is one of my recent results [5]. The proof uses a recent result of Zhu that he showed while proving the fractional version of Hedetniemi's conjecture [Zhu].

I also investigated a similar graph parameter, the independence ratio which is the ratio of the independence number and the number of vertices. I determined its asymptotic value for direct power in case of complete multipartite graphs [2], answering the question of Brown, Nowakowski and Rall [Brown et al]. In the proof I revealed the structure of independent sets and their neighbourhood in the graph power.

Similar questions are discussed in [3] co-authored with Brightwell, Cohen, Fachini, Fairthorne, Körner, Simonyi. The topic of that article is a combinatorial puzzle created by Körner and Malvenuto [Körner et al] and of further interest is that we use results related to a sequence [André, OEIS] already investigated in the 19th century.

Covering problems of edge-coloured graphs

An edge-colouring of a graph is called a Gallai colouring if there is no completely multicoloured triangle. (We can use as many colours as we want.) Investigating comparability graphs, Gallai proved remarkable theorems about edge colouring satisfying this condition [Gallai], and later this concept turned out to be relevant  in several other areas of graph theory. A basic property of Gallai colourings is that for any complete graph one can find a monochromatic component which covers the whole vertex set of the graph. Gyárfás and Sárközy showed that if we colour the edges of a not necessarily complete graph so that no 3-coloured triangles appear then there is still a large monochromatic connected component whose guaranteed size is proportional to vertex number, where the proportion depends only on the independence number of the graph. [Gyárfás et al].

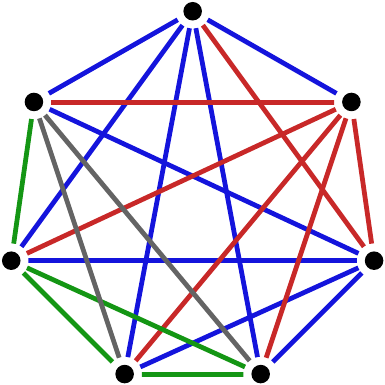
A Gallai colouring of the complete graph on seven vertices.

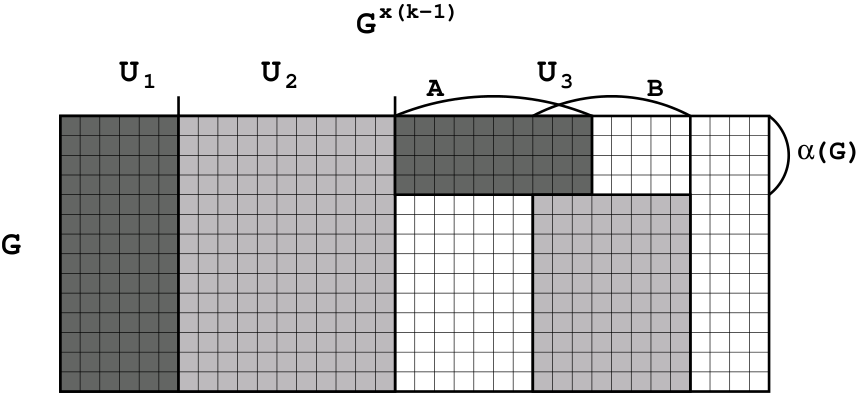
With Gyárfás and Simonyi we worked on the generalization of this result [4]. We proved that considering a Gallai colouring of any graph with a fixed independence number we can also cover the whole vertex set of the graph with finitely many connected monochromatic subgraphs. During the research, another problem about the domination number of multipartite digraphs appeared, whose solution was the key to the proof of the previous statement.

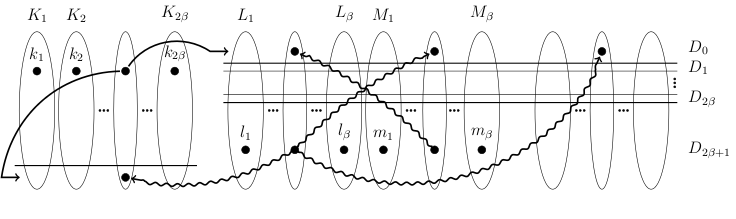
The structure which led to the solution of the domination problem. (The ellipse shaped sets are the partite classes of the multipartite graph, the arrows are the directed edges of it. Further details can be found in [4].)

As a continuation of this research with Gyárfás, Fujita and Furuya, we proved the partitioning version of this problem: we showed that the vertex set of the base graph can also be covered by a disjoint union of the vertex sets of finitely many monochromatic connected components, whose number depends only on the independence number of the graph.  We also investigated further extensions of the problem [6].

An edge coloring of a complete bipartite graph with 3 colors, such that we need 4 monochromatic components to cover the whole vertex set.

The following conjecture due to Gyárfás and Lehel is an analogue version of the Ryser conjecture for biparite graphs [Gyárfás, Lehel]. This conjecture states that if we colour the edges of a complete bipartite graph with colours then we can always find at most monochromatic connected components whose vertices cover the whole vertex set of the biparite graph. Covering with monochromatic components is easy, and there is an example showing that components are needed. The statement of the conjecture is clear for , and as a joint work with Chen, Fujita, Gyárfás and Lehel we proved the statement  for and , too [7].

Expected impact and further research

As a joint work with Gyárfás, Fujita and Furuya we are investigating the possible extensions of the recent result of Király which can be considered as a generalization of the above special case of the Ryser conjecture for hypergraphs. [Király].

We are working on further edge-colouring problems with Lesniak and Fujita [8], where we already have some partial results.

I have 3 published, 1 accepted and 1 submitted articles. I have 2 further publications in manuscript (which we plan to submit soon) and another 1 in preparation.

Publications, references, links

Publications

[1] Á. Tóth. On the ultimate lexicographic Hall-ratio. Discrete Math., 309 12 (2009), 3992–3997.

article, journal version, related talk

[2] Á. Tóth. The ultimate categorical independence ratio of complete multipartite graphs. SIAM J. Discrete Math., 23 4 (2009),  1900–1904.

article, journal version, related talk

[3] G. Brightwell, G. Cohen, E. Fachini, M. Fairthorne, J. Körner, G. Simonyi, Á. Tóth. Permutation capacities of families of oriented infinite paths. SIAM J. Discrete Math., 24 2 (2010), 441–456.

article, journal version

[4] A. Gyárfás, G. Simonyi, Á. Tóth. Gallai colorings and domination in multipartite digraphs. accepted for publication in Journal of Graph Theory

article, related talk

[5] Á. Tóth. On the ultimate direct Hall-ratio. submitted to Graphs and Combinatorics

article, related talk

[6] S. Fujita, M. Furuya, A. Gyárfás, Á. Tóth. Monochromatic tree partitions in edge-colored graphs and hypergraphs. manuscript

[7] G. Chen, S. Fujita, A. Gyárfás, J. Lehel, Á. Tóth. Around a biclique cover conjecture. manuscript

[8] L. Lesniak, S. Fujita, Á. Tóth. New results on long monochromatic cycles in edge-colored complete graphs. In preparation

Conference proceedings (their content is a part of the articles [1],[2],[5]):

• Á. Tóth. Asymptotic values of graph parameters. Proceedings of the 6th Hungarian-Japanese Symposium on Discrete Mathematics and Its Applications, Budapest, 2009., 388–392.

• Á. Tóth. On the asymptotic values of the Hall-ratio. Proceedings of the 7th Hungarian-Japanese Symposium on Discrete Mathematics and Its Applications, Kyoto, 2011., 470–472.
  

References

[André] D. André. Développement de sec x and tg x. C. R. Math. Acad. Sci. Paris, 88 (1879), 965–979.
[Brown et al] J. I. Brown, R. J. Nowakowski, D. Rall. The ultimate categorical independence ratio of a graph. SIAM J. Discrete Math., 9 (1996), 290–300.
[Cropper et al] M. Cropper, M. S. Jacobson, A. Gyárfás, L. Jenő. The Hall ratio of graphs and hypergraphs. Les cahiers du Laboratoire Leibniz., 17, 2000.
[Gallai] T. Gallai. Transitiv orientierbare Graphen. Acta Math. Sci. Hungar., 18 (1967), 25–66.
[Gyárfás] A. Gyárfás. Partition coverings and blocking sets in hypergraphs. Commun. Comput. Autom. Inst. Hungar. Acad. Sci., 71 (1977)
[Gyárfás et al] A. Gyárfás, G. N. Sárközy. Gallai colorings of non-complete graphs. Discrete Math., 310 (2010), 977–980.
[Henderson] J. R. Henderson. Permutation decomposition of (0,1)-matrices and decomposition transversals. Ph.D. Thesis, Caltech (1971)
[Király] Z. Király. Monochromatic components in edge-colored complete uniform hypergraphs. Submitted.
[Körner et al] J. Körner and C. Malvenuto. Pairwise colliding permutations and the capacity of infinite graphs. SIAM J. Discrete Math., 20 (2006), 203–212.
[Lehel] J. Lehel. Ryser’s conjecture for linear hypergraphs. manuscript, 1998.

[Lovász] L. Lovász. On the Shannon capacity of a graph. IEEE Trans. Inform., 25 (1979), 1–7.

[Shannon] C. E. Shannon. The zero-capacity of a noisy channel. IRE Trans. Inform. Theory, 2 (1956), 8–19.
[Simonyi] G. Simonyi. Asymptotic values of the Hall-ratio for graph powers. Discrete Math. 306 (2006), 2593–2601.

[Zhu] X. Zhu. Fractional Hedetniemi's conjecture is true. European J. Combin. (2011), doi:10.1016/j.ejc.2011.03.004

Links

BUTE Graduate School of Mathematics and Computer Science, Department of Computer Science and Information Theory

Useful links on the Wikipedia: graph theory, chromatic numer, fractional chromatic number, graph products.

The famous opened problems of the area: the Hedetniemi conjecture, Ryser conjecture.