Matematika- és Számítástudományok Doktori Iskola

BME VIK, Számítástudományi és Információelméleti Tanszék

Témavezető: Dr. Simonyi Gábor

Gráfszínezési problémák

A kutatási téma néhány soros bemutatása

Doktori munkám témája a gráfelmélet, ezen belül különböző gráfszínezésekkel kapcsolatos kérdések kutatása. Színezésekkel rokon gráfparaméterek különböző gráfszorzásokra vett aszimptotikus vizsgálatával, illetve különböző élszínezéssel kapcsolatos fedési problémákkal foglalkozom.

Témavezetőm Simonyi Gábor, a BME Számítástudományi és Információelméleti Tanszékének egyetemi tanára, a Rényi Alfréd Matematikai Kutatóintézetben tudományos tanácsadó.

A kutatóhely rövid bemutatása

Kutatásaimat a BME Számítástudományi és Információelméleti Tanszékén végzem. A tanszéken számos kutatás folyik elsősorban a matroidelmélet, a bonyolultságelmélet (paraméteres bonyolultság, kvantumszámítások hatékonysága), kommunikációs hálózatok megbízhatósága, VLSI hálózatok huzalozása és a deklaratív programozás területén. Hozzám hasonlóan többen foglalkoznak kombinatorikai, illetve gráfelméleti témákkal, például gráfok Hamilton-köreit, metszési számát kutatva.

A kutatás történetének, tágabb kontextusának bemutatása A gráfelmélet a matematika, ezen belül a kombinatorika egyik fontos ága. Központi fogalma a gráf, mely olyan struktúra, ami csúcsokból és az őket összekötő élekből áll. Ilyen struktúrák az élet számos területén előfordulnak: gráfokkal modellezhetők például a szociális vagy kommunikációs hálózatok, a molekulák szerkezete és a számítási folyamatok. A szemléltetés mellett a felmerülő problémák megoldásában is sokszor nélkülözhetetlen eszközként szolgálnak. Egy gráf kromatikus száma azt adja meg, hogy minimálisan hány színt kell használni a gráf csúcsainak kiszínezéséhez, hogy az összekötött csúcsok különböző színűek legyenek. Ez az egyik legtöbbet vizsgált gráfparaméter. Viselkedése egyes helyzetekben ismert, másokban teljesen tisztázatlan. A rokon paraméterek száma is igen nagy. Fontos alkalmazási területe az ütemezéselmélet. (A legegyszerűbb problémában a gráf csúcsai az ütemezendő feladatok, az élek pedig azon feladatpárokat kötik össze, melyeket különböző gépeken kell futtatnunk. Ekkor a szükséges gépek minimális száma a gráf kromatikus számával egyezik meg.)  A népszerű fejtörő, a Sudoku is megfogalmazható egy speciális gráf színezési problémájaként.

Egy biológiai hálózat gráfja (forrás).

Az öt hosszú kerékgráf optimális színezése, a gráf kromatikus száma 4.

A doktori munkám során gráfszínezésekkel kapcsolatos problémákon belül lényegében két nagyobb, elsősorban elméleti szempontból érdekes, sokat vizsgált témával foglalkozom: színezésekkel rokon gráfparaméterek különböző gráfhatványokra tekintett aszimptotikus vizsgálatával, illetve élszínezéssel kapcsolatos fedési problémákkal. Gráfelméleti problémákkal harmadévesen kezdtem el foglalkozni, tudományos diákköri munka formájában. Később ebben a témában írtam matematikus diplomamunkám, 2008 óta doktoranduszként folytatom a kutatást. Informatikus szakdolgozati témám gráfelméleti kutatásaimat segítő programok fejlesztése.

A kutatás célja, a megválaszolandó kérdések

Színezésekkel rokon paraméterek gráfszorzásokra vett aszimptotikus vizsgálata

Számos gráfparaméter esetén igaz, hogy a gráf valamilyen (gráf)szorzás szerinti hatványaiban vizsgálva a paramétert, a kapott értékek megfelelő normálásával kapott sorozat konvergens, és a határérték érdekes, új gráfparamétert ad. A gráf Shannon-kapacitása [Shannon], melynek információelméleti jelentése a csatornakapacitás elméleti felső határa hiba nélküli kódolás esetén, is ilyen módon származtatható a következő módon.

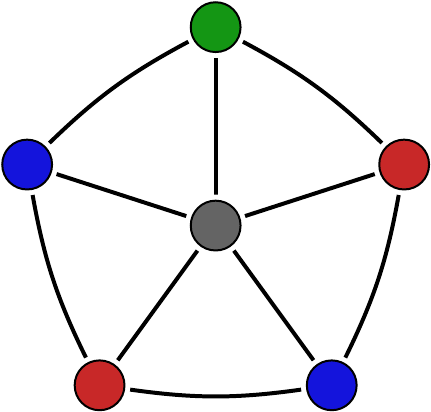
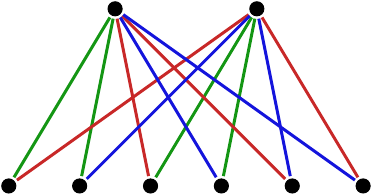
Tekintsünk példaként egy olyan csatornát, melyen ötféle karaktert küldhetünk át, de bizonyosak a csatornán lévő zaj hatására a küldés során összekeveredhetnek. Az ábrán látható gráf csúcsai a küldhető karakterek, élei az összetéveszthető párok között futnak. (Ennek alapján a küldött 'k' karakter helyett a csatorna másik végén érkezhet 'h' vagy 'b' karakter, de 'n' vagy 'p' nem.) Láthatjuk, hogy ha a csatornán visszakódolható, hiba nélküli kommunikációt akarunk megvalósítani, akkor (egyszerű esetben) olyan karaktereket kell kiválasztanunk, melyek páronként megkülönböztethetők egymástól. Ezért legfeljebb két karaktert használhatunk, két olyat, melyek nincsenek összekötve éllel. Ennél több küldhető karaktert nem választhatunk ki úgy, hogy azok között egyáltalán ne fusson él.

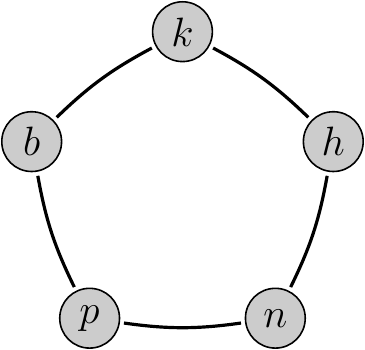Egy egyszerű csatorna összetéveszthetőségi gráfja.

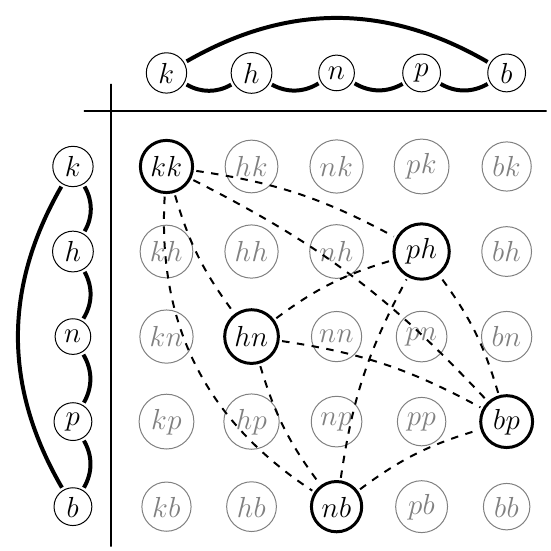Az öt hosszú kör normális szorzás szerinti négyzetében egy öt elemű független halmaz.

Észrevehetjük viszont, hogy a csatornán egyszerre több karaktert küldve  nyerhetünk, növelhetjük a csatornán időegység alatt átküldhető információ mennyiségét.  A következő öt karakterpár mind megkülönböztethető egymástól: 'kk', 'hn', 'nb', 'ph', 'bp', hiszen bármely kettőt kiválasztva vagy az első vagy a második koordinátában összetéveszthetetlen betűket találunk. Az előbbi párokat kombinálva egyszerre  karaktert küldve akár   üzenetet is küldhetünk. Sokáig nyitott kérdés volt, hogy ez-e az optimum, Lovász egyik híres eredménye annak a bizonyítása, hogy a fenti gráf, az öt hosszúságú kör Shannon kapacitása , azaz ennél nagyobb csatorna kapacitás nem érhető el, tehát karaktert használva nem küldhető -nél több megkülönböztethető üzenet, semmilyen -re [Lovász].

Általában egy gráf Shannon-kapacitása a függetlenségi szám normalizált aszimptotikus értékével definiálható ún. normális szorzás esetén. A  gráf függetlenségi száma a legnagyobb független halmazának elemszáma, ahol egy független halmaz olyan csúcsok halmaza, melyek közül semelyik kettő között nem fut él. Két gráf normális szorzata egy olyan gráf, melynek csúcsai az eredeti két gráf csúcsaiból alkotott párok, és két ilyen párt akkor kötünk össze, ha mindkét koordinátában összekötött vagy megegyező csúcsokat találunk. (Ez a szorzás éppen a fent leírt összetéveszthetőségnek felel meg a karakterekből képezhető üzenetek esetén.)

Hasonló kérdésekkel, gráfszínezésekkel rokon paraméterek különböző gráfszorzásokra vett aszimptotikus vizsgálatával foglalkozunk az [1], [2], [3], [5] cikkekben.

Élszínezésekkel kapcsolatos fedési problémák

Kutatásaim másik része különböző fedési problémákkal kapcsolatos. A terület talán legismertebb megoldatlan sejtése a Ryser-sejtés (mely először Ryser diákja, Henderson doktori dolgozatában szerepelt [Henderson]). A sejtés önmagában is vizsgált speciális esete szerint a teljes gráf éleit  színnel tetszőlegesen színezve, a gráf csúcshalmaza előáll legfeljebb  egyszínű összefüggő komponens csúcshalmazának uniójaként [Gyárfás].

A kívánt fedést komponenssel könnyedén megvalósíthatjuk, hiszen egy tetszőleges csúcsot középpontként kiválasztva az általa meghatározott legfeljebb  különböző színű csillag csúcshalmaza mindig lefedi a gráf teljes csúcshalmazát. A sejtés állítása szerint ennél eggyel kevesebb komponens is mindig elég.

Balra: A hét csúcsú teljes gráf egy élszínezése 4 színnel. Középen: Fedés négy csillag komponenssel.
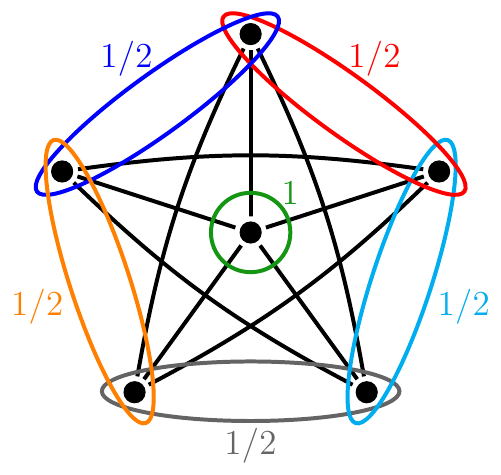
Jobbra: Fedés egyetlen egyszínű összefüggő komponenssel.

Az [4], [6], [7] dolgozatokban élszínezett gráfok egyszínű komponensekkel való fedésével foglalkozunk. 

Módszerek és eddigi eredmények

Színezésekkel rokon paraméterek gráfszorzásokra vett aszimptotikus vizsgálata

Egy gráf Hall-hányadosa a csúcsszám és a függetlenségi szám hányadosának maximuma a gráf összes részgráfjára nézve. (Például a korábban látott öt hosszú kerékgráfra a Hall-hányados értéke 3.) A fogalom bevezetését színezési problémák motiválták [Cropper et al]. Simonyi különböző gráfszorzásokra vizsgálta a paraméter aszimptotikus értékét, és megmutatta, hogy normális szorzásra a megfelelően normált aszimptotikus érték a gráf Witsenhausen hányadosa, konormális szorzásra pedig a gráf frakcionális kromatikus száma [Simonyi]. A Witsenhausen hányados a kromatikus szám aszimptotikus értéke normális szorzás esetén, és e paraméternek információelméleti jelentése is van.

A frakcionális kromatikus szám a kromatikus szám frakcionális relaxációjaként definiálható. Ez azt jelenti, hogy a gráf független halmazaira pozitív valós súlyokat tehetünk úgy, hogy a gráf minden csúcsára összesen legalább 1 súly essen; és ezen feltétel mellett szeretnénk a lehető legkevesebb összsúlyt kiosztani. A minimum értéke a gráf frakcionális kromatikus száma. (A gráf egy érvényes színezésénél  az azonos színű csúcsok mindig független halmazokat alkotnak, ezáltal ez a fogalom a kromatikus szám általánosítása. Amennyiben a fenti definícióban egész (0 vagy 1) súlyokra szorítkozunk,  azaz egy független halmazt vagy kiválasztunk vagy nem, visszakapjuk a kromatikus szám fogalmát.)

Az öt hosszú kerékgráf egy optimális frakcionális színezése, a gráf frakcionális kromatikus száma 3.5.

Diplomamunkámban beláttam, hogy lexikografikus szorzás esetén is a frakcionális kromatikus szám adódik a megfelelő sorozat határértékeként [1], ezzel igazolva Simonyi sejtését. A direkt szorzás esetén megfogalmazott analóg probléma több szempontból eltér az előzőektől; az ezen szorzásra megfogalmazott sejtést nemrég sikerült bebizonyítanom [5]. Az érvelés során Zhu egy friss eredményét is használom, melyet a Hedetniemi-sejtés frakcionális változatának igazolása közben alkalmazott [Zhu].

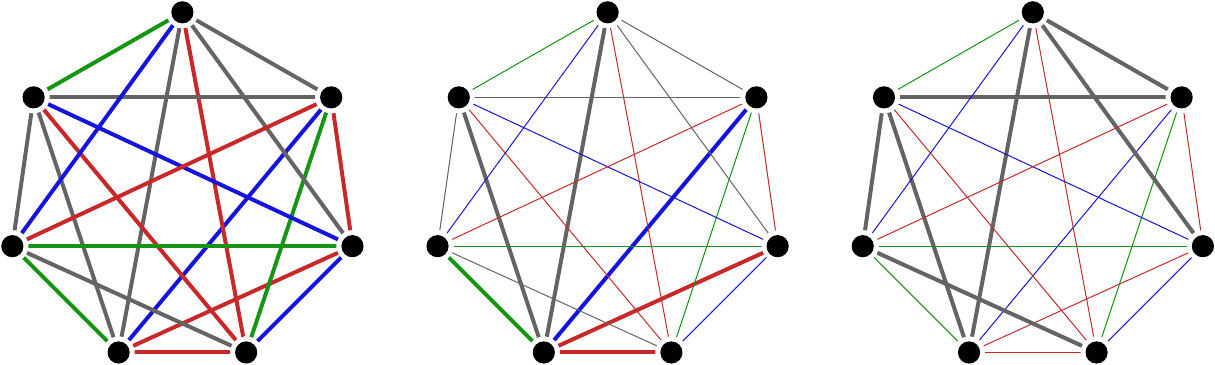
Vizsgáltam a gráf egy hasonló paraméterét, a gráf függetlenségi hányadosát is, mely a függetlenségi szám és a csúcsszám hányadosaként definiálható. Meghatároztam ezen paraméter direkt szorzásra vett aszimptotikus értékét teljes többrészes gráfokra [2], ezzel megválaszolva Brown, Nowakowski és Rall kérdését [Brown et al]. A bizonyítás során feltérképeztem a hatványgráf független halmazainak és azok szomszédságainak struktúráját.

Szintén gráfszorzásokkal kapcsolatos kérdéseket tárgyal a  Brightwell, Cohen, Fachini, Fairthorne, Körner, Simonyi társszerzőkkel írt [3] dolgozat, melynek témája egy Körner és Malvenuto által felvetett kombinatorikai kérdés [Körner et al], továbbá érdekessége, hogy egy olyan sorozattal kapcsolatos eredményeket is használ, amelyet már a 19. században is vizsgáltak [André, OEIS].

Élszínezésekkel kapcsolatos fedési problémák

Egy gráf Gallai-színezésén élek olyan színezését értjük, melyben nincs teljesen tarka háromszög, azaz amelynek mind a három éle különböző színű. (A felhasználható színek száma tetszőleges.) Összehasonlítási gráfokat vizsgálva Gallai érdekes tételeket bizonyított a feltételt kielégítő élszínezett gráfokkal kapcsolatban [Gallai], és ez a fogalom később a gráfelmélet számos más területével kapcsolatban is fontosnak bizonyult. Nem nehéz belátni, hogy teljes gráf Gallai-színezése esetén mindig van a gráfnak olyan egyszínű összefüggő komponense, mely önmagában lefedi a gráf teljes csúcshalmazát. Gyárfás és Sárközy megmutatta, hogy tetszőleges gráf Gallai-színezése esetén található olyan nagy, egyszínű összefüggő komponens, melynek mérete arányos a gráf csúcsszámával, és ez az arány csak a gráf függetlenségi számától függ, a gráf csúcsszámától vagy a felhasznált színek számától nem [Gyárfás et al].

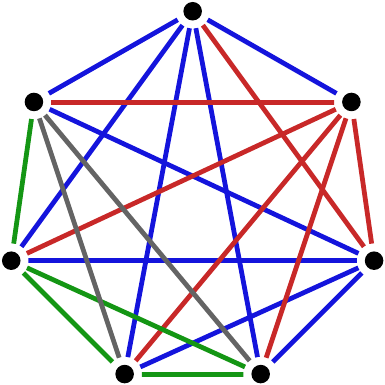
A hét csúcsú teljes gráf egy Gallai-színezése.

Gyárfással és Simonyival ezen eredmény általánosításával foglalkoztunk [4]. Igazoltuk, hogy tetszőleges gráf Gallai-színezése esetén ha a gráf függetlenségi száma rögzített, akkor a ponthalmaz lefedhető véges sok egyszínű komponenssel. A kérdés vizsgálata során egy másik, önmagában is érdekes probléma is felmerült, mely irányított többrészes gráfok dominálási kérdésével kapcsolatos, és amelynek megoldása kulcsszerepet játszott az előbbi állítás bizonyításában.

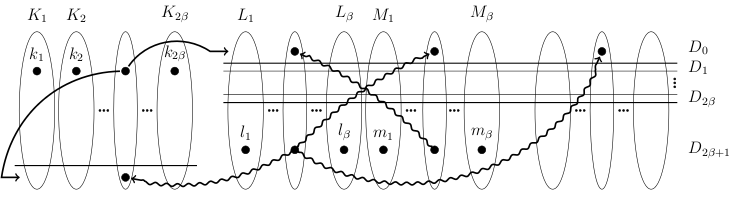
A kapcsolódó dominálási kérdés megoldásához vezető struktúra. (Az ellipszis alakú halmazok a többrészes gráf osztályai,
a nyilak az irányított éleket jelentik. További részletek [4]-ben.)

A kutatás folytatásaként Gyárfással, Fujita-val és Furuya-val bebizonyítottuk a fenti kérdés partícionálási megfelelőjét,  azaz megmutattuk, hogy az alapgráf csúcshalmaza diszjunkt módon is lefedhető véges sok egyszínű összefüggő komponens csúcshalmazával, ahol a felhasznált komponensek száma továbbra is csak a függetlenségi szám függvénye, és a gráfnak tetszőlegesen sok pontja lehet. Vizsgáltuk a problémakör további kiterjesztéseit is [6].

Egy teljes páros gráf színezése 3 színnel úgy, hogy a csúcshalmaz csak 4 egyszínű komponenssel fedhető le.

Gyárfás és Lehel fogalmazta meg a következő sejtést, mely a Ryser-sejtés páros gráfokra vonatkozó analóg verziójának tekinthető [Gyárfás, Lehel]. Tetszőleges teljes páros gráf éleit  színnel színezve, a sejtés szerint mindig található egyszínű összefüggő komponens, melyek együttesen lefedik a gráf ponthalmazát. Könnyen igazolható, hogy egyszínű komponens mindig elég, és adható olyan példa, amikor  komponensre szükség van. A sejtés állítása -ra egyszerűen adódik, Chen-nel, Fujita-val, Gyárfással és Lehellel közös kutatás eredménye, hogy az állítás igaz -re és -re is [7].

Várható impakt, további kutatás

A fenti kutatás folytatásaként Gyárfással, Fujita-val és Furuya-val vizsgáljuk Király azon friss eredményének kiterjesztéseit is, mely a Ryser-sejtés fenti speciális esetének hipergráfokra történő általánosítása [Király].

További élszínezésekkel kapcsolatos kérdéseken dolgozunk Lesniak-kal és Fujita-val [8], melyekre egyelőre részeredményeink vannak.

Jelenleg 3 megjelent, 1 elfogadott és 1 beküldött cikkem van. További 2 dolgozatom van kézirat formában (melyek terveink szerint hamarosan beküldésre kerülnek), valamint 1 előkészületben.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája

[1] Á. Tóth, On the ultimate lexicographic Hall-ratio, Discrete Math., 309 12 (2009), 3992–3997.

dolgozat, folyóirat verzió, kapcsolódó előadás

[2] Á. Tóth, The ultimate categorical independence ratio of complete multipartite graphs, SIAM J. Discrete Math., 23 4 (2009),  1900–1904.

dolgozat, folyóirat verzió, kapcsolódó előadás

[3] G. Brightwell, G. Cohen, E. Fachini, M. Fairthorne, J. Körner, G. Simonyi, Á. Tóth, Permutation capacities of families of oriented infinite paths, SIAM J. Discrete Math., 24 2 (2010), 441–456.

dolgozat, folyóirat verzió

[4] A. Gyárfás, G. Simonyi, Á. Tóth, Gallai colorings and domination in multipartite digraphs, Journal of Graph Theory, közlésre elfogadva

dolgozat, kapcsolódó előadás

[5] Á. Tóth, On the ultimate direct Hall-ratio, beküldve (Graphs and Combinatorics)

dolgozat, kapcsolódó előadás

[6] S. Fujita, M. Furuya, A. Gyárfás, Á. Tóth, Monochromatic tree partitions in edge-colored graphs and hypergraphs, kézirat

[7] G. Chen, S. Fujita, A. Gyárfás, J. Lehel, Á. Tóth, Around a biclique cover conjecture, kézirat

[8] L. Lesniak, S. Fujita, Á. Tóth, New results on long monochromatic cycles in edge-colored complete graphs, előkészületben

Konferencia kiadványban megjelent dolgozatok (tartalmuk része az [1],[2],[5] munkáknak):

• Á. Tóth, Asymptotic values of graph parameters, Proceedings of the 6th Hungarian-Japanese Symposium on Discrete Mathematics and Its Applications, Budapest, 2009., 388–392.

• Á. Tóth, On the asymptotic values of the Hall-ratio, Proceedings of the 7th Hungarian-Japanese Symposium on Discrete Mathematics and Its Applications, Kyoto, 2011., 470–472.
  

Külső hivatkozások listája

[André] D. André, Développement de sec x and tg x, C. R. Math. Acad. Sci. Paris, 88 (1879), 965–979.
[Brown et al] J. I. Brown, R. J. Nowakowski, D. Rall, The ultimate categorical independence ratio of a graph, SIAM J. Discrete Math., 9 (1996), 290–300.
[Cropper et al] M. Cropper, M. S. Jacobson, A. Gyárfás, L. Jenő, The Hall ratio of graphs and hypergraphs, Les cahiers du Laboratoire Leibniz., 17, 2000.
[Gallai] T. Gallai, Transitiv orientierbare Graphen, Acta Math. Sci. Hungar., 18 (1967), 25–66.
[Gyárfás] A. Gyárfás, Parition coverings and blocking sets in hypergraphs, Commun. Comput. Autom. Inst. Hungar. Acad. Sci., 71 (1977)
[Gyárfás et al] A. Gyárfás, G. N. Sárközy, Gallai colorings of non-complete graphs, Discrete Math., 310 (2010), 977–980.
[Henderson] J. R. Henderson, Permutation decomposition of (0,1)-matrices and decomposition transversals, Ph.D. Thesis, Caltech (1971)
[Király] Z. Király, Monochromatic components in edge-colored complete uniform hypergraphs, submitted.
[Körner et al] J. Körner and C. Malvenuto, Pairwise colliding permutations and the capacity of infinite graphs, SIAM J. Discrete Math., 20 (2006), 203–212.
[Lehel] J. Lehel, Ryser’s conjecture for linear hypergraphs, manuscript, 1998.

[Lovász] L. Lovász, On the Shannon capacity of a graph, IEEE Trans. Inform., 25 (1979), 1–7.

[Shannon] C. E. Shannon, The zero-capacity of a noisy channel, IRE Trans. Inform. Theory, 2 (1956), 8–19.
[Simonyi] G. Simonyi, Asymptotic values of the Hall-ratio for graph powers, Discrete Math. 306 (2006), 2593–2601.

[Zhu] X. Zhu, Fractional Hedetniemi's conjecture is true, European J. Combin. (2011), doi:10.1016/j.ejc.2011.03.04

Linkgyűjtemény

BME Matematika- és Számítástudományok Doktori Iskola, Számítástudományi és Információelméleti Tanszék

Hasznos szócikkek a Wikipédián: gráfelmélet, kromatikus szám, frakcionális kromatikus szám, gráfszorzások.

A terület híres nyitott kérdései: Hedetniemi-sejtés, Ryser-sejtés.