 |
BMe Kutatói pályázat |

|
Villamosmérnöki Tudományok Doktori Iskola
Híradástechnika Szakmacsoport
BME VIK, Távközlési és Médiainformatikai Tanszék
Témavezető: Dr. Cinkler Tibor
Optikai távközlő rendszerek nemlineáris eszközeinek matematikai modellezése és kísérleti vizsgálata
A kutatási téma néhány soros bemutatása
Kutatásom napjaink és a jövő optikai hálózataiban potenciálisan kihasználható kétféle nemlineáris optikai jelenségeken alapuló eszköz vizsgálatára terjed ki: ezek a telítődő abszorbensek és a periodikusan polarizált lítium-niobát (PPLN) hullámvezetők. A kutatás magában foglalja ezen eszközök fényforrásokban és jelregenerátorként való hálózati implementálhatóságának feltárását, valamint a bennük lezajló fizikai folyamatok kísérleti úton, számításokkal, matematikai modell alkotással és számítógépes szimuláció útján történő megértését.
A kutatóhely rövid bemutatása
Kutatásaimat a Távközlési és Médiainformatikai Tanszéken végzem, szoros kapcsolatban hazai és külföldi partnerekkel. A budapesti székhelyű Furukawa Electric Technológiai Intézet Kft.-vel az elméleti munkára koncentrálunk. A japán National Institute of Information and Communications Technology-val együttműködve rendszeresen odalátogató vendégkutatóink az ottani, kiemelkedően magas színvonalú Photonic Network System Laboratory-ban végzik a kísérleteket.
A kutatás történetének, tágabb kontextusának bemutatása
A kutatás két fő területet ölel fel. Az egyik a telekommunikációban [1] is alkalmazott, telítődő abszorbensre épülő, optikai szál alapú lézerek (szállézerek) számítógépes modellezése és a bennük fellépő fizikai hatások vizsgálata. A napjainkban kutatott ultrarövid (10-12 – 10-15s) impulzusú szállézerek módusszinkronizációja (az ultrarövid impulzusok keltéséhez szükséges fizikai folyamat) elsősorban passzív nemlineáris (a fényintenzitásra változó fizikai paraméterű) eszközökkel, telítődő abszorbensekkel [2] történik. Ezek az aktív [3] – optikai modulációt alkalmazó – módusszinkronizációhoz képest rövidebb impulzusokat és egyszerűbb felépítést kínálnak. Számos kísérleti vizsgálat tárgyát képezik, emellett azonban az elméleti és szimulációs munkák szerepe is fontos a lézerben zajló folyamatok együttes hatásának megértése és a lézer fontos paramétereinek előrejelzése szempontjából [4].
A másik terület a zajjal terhelt fázismodulált optikai jelek tisztán optikai fázis- és amplitúdóregenerálásának elméleti vizsgálata és kísérleti megvalósítása. A jelenlegi optikai adatátviteli rendszerekben a fázismodulált jelek regenerálását az elektromos tartományban valósítják meg [5] az optikai jeleket elektromos jellé konvertálva, majd visszaalakítva az optikai tartományba. A tisztán optikai fázisregenerálás kizárólag az optikai tartományban történik [6]. Az egyszerűbb felépítés és az alacsonyabb energiafelhasználás mellett az utóbbi módszer – tekintve, hogy a hasznosított fizikai folyamatok ultragyorsak – nem korlátozza az adatátvitel sebességét, míg az előbbinél az elektronikus eszközök gyorsasága korlátot jelent. A regeneráláshoz PPLN kristályt alkalmazunk, ami számos előnyös tulajdonsággal bír a hálózati implementáció szempontjából [7].
A kutatás célja, a megválaszolandó kérdések.
A telítődő abszorbens paramétereinek gyűrű szál oszcillátorok működésére gyakorolt hatását a saját matematikai modellemmel és annak számítógépes szimulációjával vizsgálom [8]. A vizsgálat célja, hogy a részletes matematikai tárgyalás segítségével lehetővé tegye olyan paraméterek és jelenségek együttes hatásának megértését – úgymint a telítődő abszorbens paraméterei, az oszcillátorban használt polarizációkontroll, a nemlineáris polarizáció forgatása és az oszcillátor diszperziós térképe –, amelyek az irodalomban korábban nem voltak fellelhetők. Ezen túlmenően célom feltárni a különböző impulzusparaméterek létrehozásához szükséges telítődő abszorbensbeállításokat, amelyek meghatározása kísérleti elemzéssel nehézkes volna.
A PPLN kristály fázisregenerálási tulajdonságainak vizsgálatakor kísérleti és elméleti munkát egyaránt végzek. Egyrészt célom kísérletileg megmutatni, hogy a tisztán optikai fázisregenerálás megvalósítható PPLN nemlineáris kristály felhasználásával, kihasználva a kristályban fellépő másodrendű nemlinearitásokat. Ezek a – fázisregenerálás szempontjából szintén kutatott – nemlineáris optikai szálakban fellépő harmadrendű folyamatokkal [6] analóg módon hatnak a fázismodulált jelekre, és megfelelő beállítások mellett csökkentik a fáziszajt. Emellett a PPLN-ben létrehozható többcsatornás fázisösszenyomás lehetőségét vizsgálom újszerű matematikai modellem és kísérletek alapján [9-10]. Célom annak bemutatása, hogy PPLN kristályban lehetséges több csatorna egyidejű fázisösszenyomása a nemlineáris szálhoz képest alacsonyabb áthallás mellett. Ezen tulajdonság a többhullámhosszas rendszerekben való jövőbeli használhatóság szempontjából fontos.
Módszerek
A szállézer modell magában foglalja a fényterjedés lineáris (hullámhosszfüggő) és nemlineáris effektusait az oszcillátor összes komponensében, valamint a lézererősítést leíró egyenleteket. Az oszcillátor felépítése az 1. ábrán látható.
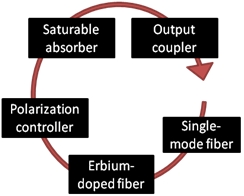
1. ábra: A modellezett oszcillátor vázlatos felépítése
A következő eszközök és jelenségek modellezését kellett megoldanom:
o Egymódusú optikai szál: a csatolt nemlineáris Schrödinger egyenletek két ortogonális, lineárisan polarizált állapotra, amelyek a rövid impulzusok terjedésének differenciálegyenletei [11].
o Egymódusú erbium adalékolású erősítőszál: az impulzusterjedés csatolt differenciálegyenletei és a lézererősítés egyenletei [12].
o Polarizációkontroller: a komponensek fázistolása mátrixos módszerrel.
o Telítődő abszorbens: gyors telítődő abszorbens közelítést alkalmazok, amelyben az eszköz csillapítása pillanatszerűen változik a fény intenzitásának függvényében.
A szálban az impulzusterjedés csatolt differenciálegyenleteinek megoldója felváltva hat a frekvenciatérben és az időtartományban, jelentős számítási idő csökkenést mutatva a véges differencia módszerekhez képest. Az adalékolt szálban a fenti egyenleteket egy lézererősítést leíró operátorral egészítem ki, a lézererősítés egyenleteinek megoldására.
Mivel a részletes matematikai modell esetenként kezelhetetlenül nagy (éves nagyságrendű) futási időket eredményez, a futások gyorsításához a Nemzeti Információs Infrastruktúra Fejlesztési Program (NIIF) debreceni szuperszámítógépét veszem igénybe.
A fázisregenerálás kísérleti megvalósítása a fázisérzékeny erősítő elvén alapszik (2. ábra).
A belépő hullámok közti kölcsönhatást a másodrendű nemlinearitások biztosítják, illetve ezek együttes hatása, amit kaszkádosított nemlinearitásnak nevezünk. A kaszkádosított nemlinearitások eredménye az első PPLN-ben másodharmonikus keltés és különbségfrekvencia keltés után a kezdeti zajból felépülő ún. idler, amely fázisban korrelált a signal-hoz és a pump-hoz, valamint a 2. PPLN-ben a fázisérzékeny erősítés. Az erősítő fáziszajjal rendelkező bináris fázismodulált (BPSK) jelek összenyomására képes (3. ábra), amit a “Phase manipulation” blokkban adunk hozzá a signal-hoz.

2. ábra: A fázisérzékeny erősítő és a fázisviszonyok
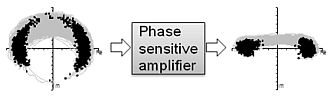
3. ábra: BPSK moduláció fáziszajának eltüntetése fázisérzékeny erősítővel
A fázisregenerálás alapvető újdonsága a fázisérzékeny erősítőhöz képest, hogy képes törölni a modulációt a bejövő modulált jelről, és az idlert előállítani az így helyreállított vivőhullámból. Ezeket felhasználva a modulált jel fázisérzékenyen erősíthető és a fáziszaja csökkenthető. Összehasonlításként, a 3. ábrán bemutatott erősítő csak egy már meglévő vivőhullám és létrehozott idler után modulált jelet tud regenerálni.
Eddigi eredmények
o Megmutattam matematikai modell és számítási eredmények alapján, hogy a vizsgált nagyfrekvenciás lézeroszcillátorban a telítődő abszorbens paraméterei milyen hatással vannak a polarizáció stabilitására, amely a legtöbb alkalmazás szempontjából kritikus paraméter. Meghatároztam azokat a lézerbeállításokat, amelyek mellett a lézer polarizációja a külső mechanikai behatások miatti a polarizáció változása esetén is stabil marad [J1].
o Kimutattam, hogy a vizsgált lézeroszcillátorban a telítődő abszorbens paraméterei együttesen hogyan befolyásolják a létrejövő, stabil polarizációjú impulzusok paramétereit. Ennek a vizsgálatnak legfőbb jelentősége az, hogy segíti az önmagában költségesebb és időigényesebb kísérleti vizsgálatot, ugyanis a laboratóriumi körülmények közt már előállított telítődő abszorbensek paraméterei nem változtathatók [J1].
o Kísérletileg megmutattam, hogy a PPLN hullámvezető felhasználásával felépített regenerátor alkalmas BPSK jelek tisztán optikai fázisregenerálására. Meghatároztam a fázisregenerálás legnagyobb hatékonyságát és a regenerátor ehhez szükséges beállításait. Megmutattam, hogy ez milyen hatással van a regenerátorban keletkező amplitúdózajra. Ezzel egy lehetséges alternatívát adtam a nemlineáris szál alapú regenerátorokra, tekintve a PPLN kedvező fizikai tulajdonságait [J2].
o Kísérletileg megmutattuk, hogy több csatorna fáziszajának egyidejű csökkentésekor PPLN-t alkalmazva a csatornák közti áthallás alacsonyabb, mint nemlineáris szálat alkalmazva. A vizsgált elrendezésekben több csatorna jelenléte nem befolyásolja számottevően egy választott csatorna regenerálásának hatékonyságát. Az eredmény a PPLN potenciális használhatóságát mutatja többhullámhosszas rendszerek regenerálásában [C1,C2].
Várható impakt, további kutatás
Kutatási eredményeim egyrészt lehetőséget nyújtanak egy megépítendő gyűrű szál oszcillátorban használt telítődő abszorbens tulajdonságainak előzetes becslésére, másrészt megvilágítják a PPLN fázismodulált jelek regenerálására történő potenciális alkalmazásait. A továbbiakban a vizsgálatokat különböző diszperziós térképekkel rendelkező oszcillátorokra és a többcsatornás fázisregenerálás matematikai modellezésére is kiterjesztem.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája:
[J1] Á. Szabó, Z. Várallyay, “Numerical Study on the Saturable Absorber Parameter Selection in an Erbium Fiber Ring Oscillator”, IEEE Photonics Technology Letters, Vol. 24, Issue 2, pp. 122-124, 2012
IMPACT FACTOR: 1.989
[J2] Á. Szabó, B. J. Puttnam, D. Mazroa, S. Shinada and N. Wada, "Investigation of an All-Optical Black-Box PPLN-PPLN BPSK Phase Regenerator", IEEE Photonics Technology Letters (submitted) 2012
[J3] Z. Várallyay, K. Saitoh, Á. Szabó, R. Szipőcs, “Photonic bandgap fibers with resonant structures for tailoring the dispersion”, Optics Express, Vol. 17, Issue 14, pp. 11869-11883, 2009
IMPACT FACTOR: 3.318
[J4] Á. Szabó, Sz. Zsigmond, T. Cinkler, ”Optimal Signal Power in CWDM Optical Networks Considering Physical Effects”, The Mediterranean Journal of Electronics and Communications, Invited paper, Vol. 6, No. 2, pp. 65-71, 2010
[J5] Á. Szabó, Sz. Zsigmond, ”Determining the Optimal Signal Power Based on Physical Effects in CWDM Optical Networks”, Infocommunications Journal, Invited paper, Hungary, vol. LXIII., 2008/7, pp. 55-59
[J6] Szabó Áron, Zsigmond Szilárd, „Optikai jelszint meghatározása CWDM hálózatokban a fizikai hatások figyelembevételével”, Híradástechnika, 63. kötet, 43-48. oldal, 2008
[C1] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada and N. Wada, "Multi-channel phase squeezing in a PPLN-PPLN PSA", Optical Fiber Communication Conference (OFC), OSA Technical Digest (Optical Society of America, 2012), paper OW3C.6
[C2] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada and N. Wada, "Signal-Signal Crosstalk Measurements in a PPLN-PPLN PSA with Narrow Channel Spacing", The 17th OptoElectronics and Communications Conference (OECC), paper accepted on 4th May, 2012
[C3] Z. Várallyay, K. Saitoh, Á. Szabó, K. Kakihara, M. Koshiba and R. Szipőcs, “Reversed dispersion slope photonic bandgap fibers and femtosecond pulse propagation”, OFC/NFOEC in San Diego, California, USA, 22-26 March 2009
[C4] Á. Szabó, Sz. Zsigmond, T. Cinkler ” Impact of Physical Effects onto the Optimal Signal Power in CWDM Optical Networks”, 6th IEEE, IET International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP)in Graz, Austria, 23-25 July, 2008
Linkgyűjtemény:
http://www.nict.go.jp/en/about/
http://www.thorlabs.com/catalogpages/693.pdf
http://aries.ucsd.edu/LMI/TUTORIALS/polarization.pdf
http://www.covesion.com/support/ppln-tutorial.html
http://www.optics.rochester.edu/users/gpa/nlfo_1h.pdf
Hivatkozások:
[1] J. W. Nicholson and D. J. DiGiovanni, “High-Repetition-Frequency Low-Noise Fiber Ring Lasers Mode-Locked With Carbon Nanotubes”, IEEE Photon. Techn. Lett. 20 (24), pp. 2123-2125 (2008)
[2] T. Tsai, Y. Fang, and S. Hung, "Passively Q-switched erbium all-fiber lasers by use of thulium-doped saturable-absorber fibers," Opt. Express 18, 10049-10054 (2010)
[3] H. A. Haus, “A theory of forced mode locking”, IEEE J. Quantum Electron. QE-11, 323 (1975)
[4] T. Schreiber, B. Ortaç, J. Limpert, and A. Tünnermann, "On the study of pulse evolution in ultra-short pulse mode-locked fiber lasers by numerical simulations," Opt. Express 15, 8252-8262 (2007)
[5] Cotter, D., Manning, R., Blow, K., Ellis, A., Kelly, A., Nesset, D., Phillips, I., et al., “Nonlinear Optics for High-Speed Digital Information Processing”, Science 286 (5444), 1523-1528 (1999)
[6] R. Slavík, F. Parmigiani, J. Kakande, C. Lundström, Martin Sjödin, Peter A. Andrekson, Ruwan Weerasuriya, et al. „All-optical phase and amplitude regenerator for next-generation telecommunications systems”. Nat. Photon. 4 (10), 690-695 (2010)
[7] B. Puttnam, D. Mazroa, S. Shinada, and N. Wada, "Phase-squeezing properties of non-degenerate PSAs using PPLN waveguides," Opt. Express 19, B131-B139 (2011)
[8] Á. Szabó and Z. Várallyay, “Numerical Study on the Saturable Absorber Parameter Selection in an Erbium Fiber Ring Oscillator”, IEEE Phot. Techn. Lett. 24 (2), 122-124 (2012)
[9] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada, and N. Wada, "Multi-channel phase squeezing in a PPLN-PPLN PSA," in Optical Fiber Communication Conference, OSA Technical Digest (Optical Society of America, 2012), paper OW3C.6.
[10] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada, and N. Wada, “Signal-signal Crosstalk Measurements in a PPLN-PPLN PSA with Narrow Channel Spacing”, OptoElectronics and Communications Conference (OECC) Jul. 02-06 (2012)
[11] G. P. Agrawal, Nonlinear Fiber Optics,
(Academic, 4th edition, 2007)
[12] C. R. Giles and Emmanuel Desurvire,
“Modeling Erbium-Doped Fiber Amplifiers”, Journ. of
Lightw. Techn. 9 (2), 271-283 (1991)
