 |
BMe Research Grant |

|
Doctoral School of Electrical Engineering
Faculty of Telecommunication
Department of Telecommunications and Media Informatics
Supervisor: Dr. Tibor Cinkler
Mathematical modeling and experimental study of nonlinear optical devices in optical transmission systems
Brief introduction of the research field
My research focuses on two nonlinear optical devices potentially used in today’s and in future optical networks: the saturable absorbers and the periodically poled lithium niobate (PPLN) waveguides. The research involves the investigation of potential applicability of these devices as light sources and signal regenerators and the understanding of the underlying physical phenomenons via experiments, calculations, mathematical modeling and computer simulation.
Short introduction of the place of research
I conduct my research at the Department of Telecommunications and Media Informatics, in intense collaboration with various domestic and foreign partners. The common work with the Furukawa Electric Institute of Technology Ltd. based in Budapest focuses on theory. In the frame of cooperation with the National Institute of Information and Communications Technology based in Japan, our visiting researchers do experimental work on a regular basis at the Photonic Network System Laboratory, renown for their high standard.
The history of the research and a wider context
My research work covers two main areas. The first one is the investigation of physical processes in optical fiber based lasers (fiber lasers) utilizing saturable absorbers via computer simulation. These fiber lasers are used e. g. for telecommunication purposes [1]. The mode locking (the physical process needed for the ultra short pulse generation) of the ultra short (10-15 – 10-12) pulsed fiber lasers investigated nowadays is based mainly on passive nonlinear devices (the physical parameters of which change as a function of light intensity), namely saturable absorbers [2]. This kind of mode locking allows for the generation of shorter pulses and a simpler laser build-up, compared to the actively mode-locked lasers [3] utilizing optical modulation. Passively mode-locked lasers have been intensively researched experimentally, however, their theoretical investigation is also important in understanding the joint effect of the physical processes and in forecasting important laser parameters [4].
The other main area is the theoretical study and experimental realization of the all-optical phase and amplitude regeneration of phase modulated signals deteriorated by phase and amplitude noise. In today’s optical transmission systems, the regeneration of the phase modulated signals is executed in the electrical domain, converting the optical signals to electrical ones and back [5]. The all-optical phase regeneration is executed solely in the optical domain [6]. This not only allows for a simpler regenerator build-up and lower power consumption, but also the use of practically unlimited data transmission rates thanks to the ultra fast physical processes utilized. In the regular regeneration method, data transmission rate is limited by the speed of the electronic devices. We utilize PPLN crystals for the phase regeneration, which has many advantages in terms of network implementation [7].
Aims of research
I investigate the effect of the saturable absorber parameter selection on the operation of fiber ring oscillators using my own mathematical model and its computer simulation [8]. The purpose of the study is to understand based on a detailed mathematical model the joint effect of parameters and physical processes – such as saturable absorber parameters, polarization control in the oscillator, nonlinear polarization rotation and different dispersion maps – that has not been studied as a whole in the literature as yet. Moreover, another aim is to reveal the saturable absorber setups required for creating different pulse parameters, which would be difficult experimentally.
When investigating the PPLN crystal's phase regeneration properties I do both theoretical and experimental work. On the one hand, my goal is to show experimentally that all-optical phase regeneration can be realized using PPLN nonlinear crystals, exploiting the second order nonlinearities in it. These processes are in analogy with the third order nonlinearities appearing in highly nonlinear fibers [6], also investigated in the scope of phase regeneration, and at appropriate settings they reduce the phase noise level. Moreover, I investigate the potential of multichannel phase squeezing in PPLN using my novel mathematical model and experimental results [9-10]. My aim is to show that it is possible to phase-squeeze multiple channels in a PPLN with lower crosstalk compared to the nonlinear fiber. This feature of the PPLN is useful especially for potential future applications in multi-wavelength systems.
Methods
The fiber laser model involves the linear (wavelength dependent) and nonlinear effects of light propagation in every components of the oscillator, and the equations of laser amplification. The build-up of the oscillator can be seen in Fig. 1.
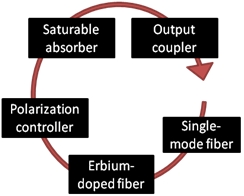
Fig. 1: The draft of the modeled oscillator
I had to solve the problem of modeling the following devices and effects:
-
o Single mode fiber: the coupled nonlinear Schrödinger’s equations for two orthogonally polarized states, which are the differential equations for the propagation of short pulses [11].
-
o Single mode erbium doped fiber for light amplification: coupled differential equations for pulse propagation and the equations of laser amplification [12].
-
o Polarization controller: the phase shift of the components by matrix method.
-
o Saturable absorber: I use a fast saturable absorber approximation, in which the absorption of the device changes momentarily as a function of the light intensity.
In the fiber, the solver of the coupled differential equations acts alternated in the time domain and in the frequency domain, significantly speeding up calculations compared to the finite difference methods. In the doped fiber a laser amplification operator is added to the above equations, which solves the equations of the laser amplifications.
Since the detailed mathematical model requires unmanageably long calculation times (the order of magnitude of years) in certain cases, I used the supercomputer of Nemzeti Információs Infrastruktúra Fejlesztési Program (NIIF) in Debrecen to speed up the calculations.
The experimental realization of the phase regeneration is based on the principle of phase sensitive amplifier (Fig. 2). The interaction between the incoming waves is assured by the second order nonlinearities and their joint effect, which is called cascaded nonlinearities. As a result of cascaded nonlinearities, a so-called idler builds up from the initial noise in the first PPLN after second harmonic and difference frequency generation. The idler is phase correlated with the signal and the pump. The cascaded processes also cause the phase sensitive amplification in the second PPLN. The amplifier is able to squeeze binary phase shift keyed (BPSK) signals with additional phase noise (Fig. 3), which was added to the signal in the “Phase manipulation” stage.

Fig. 2: The phase sensitive amplifier and phase relationships
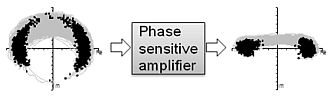
Fig. 3: Elimination of phase noise of BPSK modulation by phase sensitive amplifier
Results obtained so far
o Based on the mathematical model and calculation results, I have identified the effects of the saturable absorber parameters on the stability of polarization in the high frequency laser oscillator applied. This behavior is critical for most laser applications. I calculated the settings of the laser which assures constant output polarization of the laser even if polarization changes by mechanical stress [J1].
o For the investigated oscillator I have shown the joint effect of the saturable absorber parameters on the pulse properties in stable polarization cases. The result is important in experimental studies, which are more costly and time consuming on their own, since the parameters of a saturable absorber built in a lab cannot be changed later [J1].
o I have shown experimentally that the phase regenerator utilizing PPLN waveguides is able to regenerate BPSK signals in an all-optical way. I have determined the maximum efficiency of phase regeneration and the related regenerator settings. I have shown the effect of these settings on the additional amplitude noise in the regenerator. Consequently, I proposed a possible alternative to nonlinear fiber based regenerators, considering the favorable properties of PPLNs [J2].
o We have shown experimentally that reducing the phase noise of multiple channels simultaneously using a PPLN results in lower inter-channel crosstalk than using a nonlinear fiber. In the investigated setups, the presence of multiple channels did not affect significantly the phase squeezing efficiency of any given channel. This result supports the potential use of PPLN-based regenerators for multi-wavelength systems [C1, C2].
Expected impact, further research
My research results, on the one hand, make it possible to forecast the saturable absorber parameters of a fiber laser oscillator to be built. On the other hand, they reveal the potential use of PPLNs in the regeneration of phase modulated signals. In my further research I'll include oscillators with different dispersion maps, and the mathematical modeling of multichannel phase regeneration.
Own publications, references, collection of links
Own publications
[J1] Á. Szabó, Z. Várallyay, “Numerical Study on the Saturable Absorber Parameter Selection in an Erbium Fiber Ring Oscillator”, IEEE Photonics Technology Letters, Vol. 24, Issue 2, pp. 122-124, 2012
IMPACT FACTOR: 1.989
[J2] Á. Szabó, B. J. Puttnam, D. Mazroa, S. Shinada and N. Wada, "Investigation of an All-Optical Black-Box PPLN-PPLN BPSK Phase Regenerator", IEEE Photonics Technology Letters (submitted) 2012
[J3] Z. Várallyay, K. Saitoh, Á. Szabó, R. Szipőcs, “Photonic bandgap fibers with resonant structures for tailoring the dispersion”, Optics Express, Vol. 17, Issue 14, pp. 11869-11883, 2009
IMPACT FACTOR: 3.318
[J4] Á. Szabó, Sz. Zsigmond, T. Cinkler, ”Optimal Signal Power in CWDM Optical Networks Considering Physical Effects”, The Mediterranean Journal of Electronics and Communications, Invited paper, Vol. 6, No. 2, pp. 65-71, 2010
[J5] Á. Szabó, Sz. Zsigmond, ”Determining the Optimal Signal Power Based on Physical Effects in CWDM Optical Networks”, Infocommunications Journal, Invited paper, Hungary, vol. LXIII., 2008/7, pp. 55-59
[J6] Szabó Áron, Zsigmond Szilárd, "Optikai jelszint meghatározása CWDM hálózatokban a fizikai hatások figyelembevételével” (in Hungarian), Híradástechnika, vol. 63., pp. 43-48, 2008
[C1] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada and N. Wada, "Multi-channel phase squeezing in a PPLN-PPLN PSA", Optical Fiber Communication Conference (OFC), OSA Technical Digest (Optical Society of America, 2012), paper OW3C.6
[C2] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada and N. Wada, "Signal-Signal Crosstalk Measurements in a PPLN-PPLN PSA with Narrow Channel Spacing", The 17th OptoElectronics and Communications Conference (OECC), paper accepted on 4th May, 2012
[C3] Z. Várallyay, K. Saitoh, Á. Szabó, K. Kakihara, M. Koshiba and R. Szipőcs, “Reversed dispersion slope photonic bandgap fibers and femtosecond pulse propagation”, OFC/NFOEC in San Diego, California, USA, 22-26 March 2009
[C4] Á. Szabó, Sz. Zsigmond, T. Cinkler ” Impact of Physical Effects onto the Optimal Signal Power in CWDM Optical Networks”, 6th IEEE, IET International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP)in Graz, Austria, 23-25 July, 2008
Collection of links:
http://www.nict.go.jp/en/about/
http://www.thorlabs.com/catalogpages/693.pdf
http://aries.ucsd.edu/LMI/TUTORIALS/polarization.pdf
http://www.covesion.com/support/ppln-tutorial.html
http://www.optics.rochester.edu/users/gpa/nlfo_1h.pdf
References:
[1] J. W. Nicholson and D. J. DiGiovanni, “High-Repetition-Frequency Low-Noise Fiber Ring Lasers Mode-Locked With Carbon Nanotubes”, IEEE Photon. Techn. Lett. 20 (24), pp. 2123-2125 (2008)
[2] T. Tsai, Y. Fang, and S. Hung, "Passively Q-switched erbium all-fiber lasers by use of thulium-doped saturable-absorber fibers," Opt. Express 18, 10049-10054 (2010)
[3] H. A. Haus, “A theory of forced mode locking”, IEEE J. Quantum Electron. QE-11, 323 (1975)
[4] T. Schreiber, B. Ortaç, J. Limpert, and A. Tünnermann, "On the study of pulse evolution in ultra-short pulse mode-locked fiber lasers by numerical simulations," Opt. Express 15, 8252-8262 (2007)
[5] Cotter, D., Manning, R., Blow, K., Ellis, A., Kelly, A., Nesset, D., Phillips, I., et al., “Nonlinear Optics for High-Speed Digital Information Processing”, Science 286 (5444), 1523-1528 (1999)
[6] R. Slavík, F. Parmigiani, J. Kakande, C. Lundström, Martin Sjödin, Peter A. Andrekson, Ruwan Weerasuriya, et al. "All-optical phase and amplitude regenerator for next-generation telecommunications systems”. Nat. Photon. 4 (10), 690-695 (2010)
[7] B. Puttnam, D. Mazroa, S. Shinada, and N. Wada, "Phase-squeezing properties of non-degenerate PSAs using PPLN waveguides," Opt. Express 19, B131-B139 (2011)
[8] Á. Szabó and Z. Várallyay, “Numerical Study on the Saturable Absorber Parameter Selection in an Erbium Fiber Ring Oscillator”, IEEE Phot. Techn. Lett. 24 (2), 122-124 (2012)
[9] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada, and N. Wada, "Multi-channel phase squeezing in a PPLN-PPLN PSA," in Optical Fiber Communication Conference, OSA Technical Digest (Optical Society of America, 2012), paper OW3C.6.
[10] B. J. Puttnam, Á. Szabó, D. Mazroa, S. Shinada, and N. Wada, “Signal-signal Crosstalk Measurements in a PPLN-PPLN PSA with Narrow Channel Spacing”, OptoElectronics and Communications Conference (OECC) Jul. 02-06 (2012)
[11] G. P. Agrawal, Nonlinear Fiber Optics,
(Academic, 4th edition, 2007)
[12] C. R. Giles and Emmanuel Desurvire,
“Modeling Erbium-Doped Fiber Amplifiers”, Journ. of
Lightw. Techn. 9 (2), 271-283 (1991)
