 |
BMe Kutatói pályázat |
|
Informatikai Tudományok Doktori Iskola
BME VIK, Távközlési és Médiainformatikai Tanszék
Témavezető: Dr. Gulyás András
Komplex hálózatok vizsgálata játékelméleti módszerekkel
A kutatási téma néhány soros bemutatása
A komplex hálózatok elméletében központi szerepet játszik a mohó (greedy) navigáció, mivel megfelelő topológia esetén hatékony kommunikáció valósítható meg mohó algoritmusok használatával. Habár számos kutatás foglalkozik routing- és topológiageneráló algoritmusok létrehozásával, a mohó kommunikációt használó hálózatok kialakulásáról a mai napig keveset tudunk. Ennek ismerete teljesen új szemlélethez segítheti a szakembereket, mely hatékonyabb algoritmusokat eredményezhet.
Kutatásaimban játékelméleti módszerek segítségével vizsgálom a komplex hálózatok kialakulását, mohó navigáció esetén.
A kutatóhely rövid bemutatása
A kutatást PhD hallgatóként, a Távközlési és Médiainformatikai Tanszéken (TMIT), a High Speed Network Laboratory (HSN Lab) keretein belül végzem, melyet a tanszék az Ericssonnal közösen hozott létre 1992-ben. A tudományos tevékenység színvonalát jól jelzi a publikációk száma és minősége.
A kutatás történetének, tágabb kontextusának bemutatása
A komplex hálózatok tanulmányozása a hálózattudomány egyik legfontosabb területe, mivel a természetben előforduló hálózatok (biológiai, szociális, gazdasági, technológiai) többsége és az Internet is komplex hálózat. Minden hálózatot egy gráffal reprezentálhatunk, melyet általában három alapvető megközelítésből vizsgálhatunk: struktúra, navigáció, kialakulás.
Struktúra
Alapvető strukturális tulajdonságok a fokszámeloszlás, átmérő és klaszterezettségi együttható. Mára a kezdetben kevésbé valósághű modelleket (Erdős-Rényi modell [1], Watts és Strogatz-féle kisvilág modell [2]) már olyan pontos, az igazi hálózatokat tökéletesen utánzó modellek váltották fel, mint a Barabási-féle skálafüggetlen modell [3], a véletlen bejáráson alapuló modellek, a fraktális modellek, illetve a metrikus tér alapú modellek.
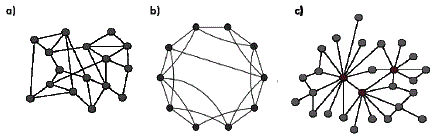
1. ábra: A legalapvetőbb hálózati modellek: a) Erdős-Rényi-féle véletlen modell, b) Watts és Strogats-féle kisvilág modell, c) Barabási-féle skálafüggetlen modell
Navigáció
Stanley Milgram 1967-es kísérlete [4] megmutatta, hogy a komplex hálózatok hatékony kommunikációs jellemzői a kisvilág tulajdonság és a mohó navigáció együttes jelenlétének köszönhető. [2,4] A mohó navigáció általánosan úgy jellemezhető, hogy az út során minden lépésnél az adott szempontból legjobbnak tűnő irányba haladunk. Mivel a módszer nem globálisan optimális, használhatósága éppen ezért nem kézenfekvő. A témával foglalkozó kutatási eredmények a komplex hálózatok mögött úgynevezett rejtett metrikus tér [5] feltételezésével sikeresen magyarázzák az algoritmus hatékony működését. A metrikus tér segítségével minden csomópont között távolság számítható, s mohó navigáció során egy csomópont mindig ahhoz a szomszédjához továbbítja üzenetét, mely a legközelebb található a célcsomóponthoz (ezáltal lehetővé téve a kizárólag lokális információkra alapozott kommunikációt).
Az első analitikus modellt [5] Jon Kleinberg készítette 2000-ben, mely egy D-dimenziós Euklideszi rácson magyarázta a kísérlet jelenségeit. A legutóbbi modellek már nem Euklideszi tereken alapulnak, s a navigációs tulajdonságok mellett képesek leírni bizonyos strukturális tulajdonságokat is.
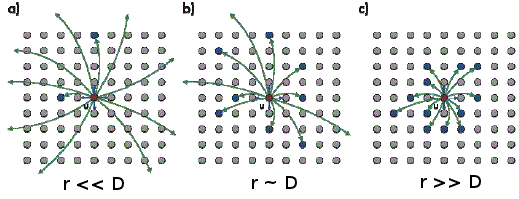
2. ábra: A Kleinberg modell által létrehozott különböző hálózati struktúrák az úgynevezett homophília paraméterrel (r) hangolhatóak. Kleinberg fő eredménye, hogy ha r ~ D (vagyis a dimenziószám), akkor a közösségi hálózatokhoz hasonló topológiát kapunk.
Kialakulás:
Míg a komplex hálózatok strukturális és navigációs jellemzőivel ma már többé-kevésbé tisztában vagyunk, addig létezésük magyarázata egyelőre a legnagyobb kihívások egyikének tűnik. A Hálózatformációs Játékok (Network Formation Games [6]) az egyik legígéretesebb keretrendszer, mellyel erre a kérdésre a választ keresik, s ugyan számos érdemes eredmény született, de a mai napig sem sikerült Nash egyensúlyként komplex hálót előállítani. A problémát a tématerület legátfogóbb műve az Algorithmic Game Theory [7] c. könyv is a legfontosabbak között említi.
A kutatás célja, a megválaszolandó kérdések.
Célom a játékelmélet módszertanának használatával a komplex hálózatok mélyebb megértése, létrejöttük vizsgálata. Ennek fontos lépése olyan valósághű modellek megalkotása, melyek (Nash) egyensúlyi állapotai komplex hálózatokat eredményeznek. Ennek során számos problémát kell megoldani, ezek közé tartozik a megfelelő játékok definiálása, a modellek helyességének alátámasztása analitikus módszerekkel és szimulációkkal, továbbá a létrehozott modellek elemzése.
Módszerek
Hálózatformációs játékok
Az egyes játékok során racionális (“önző”) játékosokat feltételezünk, akik kölcsönös interakciójuk eredményeként egy hálózatot formálnak. Az alapkérdések:
- Melyek az egyensúlyi hálózati formák?
- Mekkora a költsége az egyensúlyi állapotoknak?
Egy játék definiálásához három összetevő szükséges:
Játékosok: Legyen P a játékosok halmaza, melynek számossága N, A játékosokat a
gráf csomópontjai reprezentálják, melyeket elhelyezünk egy D-dimenziós térben.
Ekkor minden játékost egyértelműen azonosíthatunk egy
vektorral, s bármely két
játékos között távolságot számíthatunk a legrövidebb út távolságmetrika
alapján.
Stratégiák: egy csomópont stratégiái irányított élek húzása a gráf többi
csomópontjához. Egy
játékos stratégia tere
. Legyen s egy adott stratégiavektor:
. A játékosok egyéni stratégiájának összessége meghatározza a
hálózatot a játék egy adott állapotában:
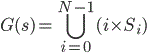
Kifizetés: minden játékos rendelkezik egy költségfüggvénnyel:
A játékosok célja saját költségfüggvényük minimalizálása. A költségfüggvény két összetevőből áll, az első tag a kommunikációs költséget jelenti (milyen hosszú utakon keresztül éri el két játékos egymást), a második pedig a hálózatkiépítési költséget (a játékos által létrehozott élek összköltsége).
Eszközök a játék elemzéséhez
- Nash egyensúly (NE): azt az állapotot jelöli a játék során, amikor egyetlen játékosnak sem érdeke a saját stratégiájának megváltoztatása, abban az esetben, ha a többi játékos sem változtat a sajátján.
- Social optimum (SO): az optimális egyensúlyi állapot költségét mutatja, vagyis amikor a költségfüggvények összege minimális, akár annak árán, hogy az így előállt egyensúlyi állapot eléréséhez központi irányítás szükséges.
- Price of Anarchy: azt a költséget mutatja,
amit legrosszabb esetben fizethetnek a játékosok a központi koordináció
hiányáért. Számítása:
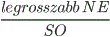
- Price of Stability: azt a költséget mutatja,
amit mindenképpen fizetniük kell a játékosoknak egy egyensúlyi állapot
eléréséhez. Számítása:
Eddigi eredmények
Feltételezésünk szerint a létező hálózatformációs játékok azért nem képesek komplex hálózatot létrehozni egyensúlyi állapotban, mert a kommunikációs költséget a legrövidebb utak hossza alapján számolják, ami nem realisztikus. Az általunk definiált Mohó Hálózatformációs Játékban (Greedy Network Formation Game) az eddigi legrövidebb út alapú távolságmetrikát mohó alapú távolságmetrikára cseréltük, majd analitikus módszerekkel megmutattuk, hogy a számos routing algoritmus alapját képező Kleinberg modell nem áll elő Nash egyensúlyként a játék során, vagyis a valós világban nem alakul ki a modell konstans dimenziós Euklideszi teret feltételezve.
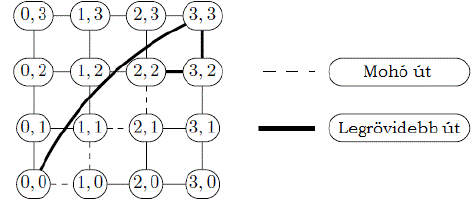
4. ábra: Mohó és legrövidebb út közötti különbség 2D-s Euklideszi rács esetén a (2,2) és (0,0) pontok között
Továbblépésként újradefiniáltuk a játékot hiperbolikus tér felett, s a játék elemzése azt mutatja, hogy ezzel a változtatással a játék egyensúlyi állapotaként szinte természetes módon előállnak realisztikus skálafüggetlen topológiák.
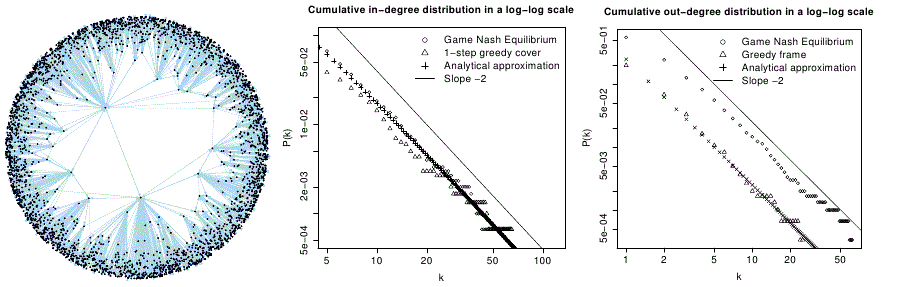
4. ábra: Egyensúlyi topológia (balra), bemenő fokszámeloszlás (középen), kimenő fokszámeloszlás (jobbra)
Várható impakt, további kutatás
A komplex hálózatok kialakulásának megértése lehetővé teszi a hálózatokon lezajló jelenségek előrejelzését, a hálózat részleges irányítását és a telekommunikáció területén hatékonyabb routing és policy algoritmusok fejlesztését. A mohó keresésen alapuló hálózati megoldások elosztottsága, rendkívüli hibatűrése, az alacsony adminisztrációs költségek, illetve a gyorsabb és egyszerűbb működés és a lokalitás, infokommunikációs szempontból mind nagyon kívánatos tulajdonságok.
A létrehozott játékok elemzése jó alapot adhat az Interneten jelenleg alkalmazott BGP (Border Gateway Protokoll) [8] topológiára gyakorolt hatásának vizsgálatához. A BGP összehasonlítása a mohó és a valley free routing [9] mechanizmussal ugyancsak érdekes, aktuális kérdés.
Saját publikációk, hivatkozások, linkgyűjtemény
Saját publikációk
[Sz1] Szabó, Dávid, “Önmagát szervező egyetemi hálózat”, TDK dolgozat, BME - VIK 2010, II. helyezés
[Sz2] Szabó Dávid, Gulyás András, Csernai Márton, Heszberger Zalán, “Skálafüggetlen címzésen alapuló önszerveződő útvonal-választási architektúra”, Híradástechnika, 2011.
[Sz3] David Szabo, Marton Csernai, “Self organizing structurless routing architecture”, POSTER konferencia, 2011
[Sz4] Szabó Dávid, Gulyás András, “Jelterjedési utak topológiára gyakorolt hatásának vizsgálata játékelméleti módszerekkel”, Mesterpróba konferencia, 1. helyezés, 2012
[Sz5] Andras Gulyas, Attila Korosi, Gergely Biczok, David Szabo, "On Greedy Network Formation", ACM SIGMETRICS W-PIN WS, 2012
[Sz6] Andras Gulyas, Attila Korosi, Gabor Retvari, Jozsef Biro, David Szabo, "Brief Announcement: Network Formation Games Can Give Rise to Realistic Network", PODC (Principles of Distributed Computing), 2012
[Sz7] Andras Gulyas, Attila Korosi, Gergely Biczok, David Szabo, "On Greedy Network Formation", to appear at ACM SIGMETRICS Performance Evaluation Review
Hivatkozások
[1] Erdös P. & Rényi, A. (1959) Publ. Math. 6 , 290-297
[2] D.J. Watts, P.S. Dodds, and M.E.J. Newman, “Identity and search in social networks”, Science, 296(5571):1302, 2002.
[3] Albert-László Barabási, Réka Albert, Hawoong Jeong, “Mean-field theory for scale-free random networks”, Physica A: Statistical Mechanics and its Applications, Volume 272, Issues 1-2, Octorber 1999, Pages 173-187
[4] J. Travers and S. Milgram. An experimental study of the small world problem. Sociometry, 32:425–443, 1969.
[5] J. Kleinberg. The small-world phenomenon: an algorithm perspective. In Proc. of STOC’00, pages 163–170, 2000.
[6] Alex Fabricant, Ankur Luthra, Elitza Maneva, "On a Network Creation Game", PODC 2003, Pages 347-351
[7] Noam Nisan, “Algorithmic Game Theory”, 2007
[8] G. Huston, Analyzing the Internet's BGP routing table, potaroo.net, 2001, http://www.potaroo.net/papers/ipj/4-1-bgp.pdf
[9] Qiu, S.Y., Johns Hopkins, McDaniel, P.D., Monrose, F., "Toward Valley-Free Inter-domain Routing", Communications, 2007. ICC '07. IEEE International Conference, 2007
Linkgyűjtemény
Távközlési és Médiainformatikai Tanszék (TMIT) honlapja
High Speed Network Laboratory (HSN Lab) honlapja
Watts és Strogatz-féle kisvilág modell
Barabási-féle skálafüggetlen modell