 |
BMe Research Grant |

|
Doctoral School of Informatics
Department of Telecommunications and Media Informa
Supervisor: Dr. Gulyás András
Game theoretical analysis of the emergence of complex networks
Abstract
Greedy navigability is a central issue in the theory of complex networks, since over the appropriate topology greedy algorithms can operate extremely well in the course of communication. In the last decade the structural and navigational aspects of networks have been in the mainstream of research, however, less is known about how greedy-routable networks emerge among real conditions. Having insight into the emergence of such networks could provide completely new approaches and result in better predictability and control or eventuate more effective algorithms. In my research I examine the emergence of complex networks in case of greedy navigation in a game theoretic manner.
Workplace
I work at the Dept. of Telecommunications and Media Informatics in High Speed Network Laboratory (HSN Lab) as a PhD student. The Lab was established in 1992 in the cooperation of the Department and Ericcson. The number and the quality of publications indicative of high standard.
The context of the research
The analysis of complex networks is one of the most important areas of network science, since most of the real-world networks (biological, social, economical, technological) and the Internet fall under this classification. Networks are generally represented by graphs and their analysis is focused mainly on three aspects: structure, navigation, and emergence.
Structure
The characteristic structural properties are the degree distribution, diameter and clustering coefficient. Nowadays, the old, less realistic models (Erdős-Rényi model [1], Watts and Strogatz small world model [2]), have been replaced with new models (Barabási scale-free model [3], random walk-based models, fractal models, metric space models), which can mimic almost any kind of structural artifact a real network may have.
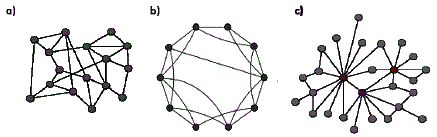
Fig. 1: The most standard network models: a) Erdős-Rényi random model, b) Watts and Strogats small world model, c) Barabási scale-free model
Navigation
Milgram's famous experiment [4] was the first to show empirical evidence that complex networks are small worlds and navigable by distributed greedy algorithms at the same time. [2,4] In the course of greedy navigation, a node always chooses that neighbor which seems the best choice. This method is not a globally optimal algorithm, hence it’s application is not trivial. According to recent research efforts, assuming a hidden metric space [5] behind networks seems to be a plausible explanation for the effective communication. With the metric space we can calculate the distance between two arbitrarily chosen nodes, and so greedy navigation chooses the node which is closest to the target node (so the communication based only local information).
Jon Kleinberg was the first in 2000, who proposed an analytic model based on D dimensional Euclidean lattices [5], for explaining the results of Milgram’s experiment. More recent models propose using non-Euclidean geometry and additionally to navigational properties they can characterize some structural properties, too.
.

Fig. 2: The different topologies can be generated by setting the value of the so-called homophily parameter (r). Kleinberg’s main result was that if r ~ D (the number of dimensions), then we get a navigable topology
Emergence:
While the structural and navigational properties of the complex networks are more or less well known, the explanation for their existence seems to be one of the greatest challenges. The Network Formation Games [6] is a promising framework, which can help find the answer to this question. The research in this direction produced numerous sharp results, but for the present there does not exist a game whose Nash equilibrium states are complex networks. The influential book on the subject “Algorithmic Game Theory” [7] also names the problem one of the most important questions.
Research goals and questions to be answered
My research is focused on the examination of the emergence of complex networks in a game theoretical manner. An important step in this direction is to create realistic models from which complex networks readily emerge as Nash equilibria. There are several problems to be solved to proceed: defining appropriate games, validating the models with analytical methods and simulation, furthermore we have to analyses the emerging topologies.
Methodology
Network Formation Games
In this framework there are rational (“selfish”) players forming a network by their interactions. The main questions are:
- Which are the equilibrium topologies?
- How much is the cost of the equilibrium?
For defining a game we need the following three components:
Players: Let P be the set of players with cardinality N. The nodes of the graph
represent the players, which we place in a D-dimensional space. So every node
has a coordinate which localize it uniquely with an
![]() vector, and we can
calculate the distance between arbitrarily chosen nodes based on shortest path
distance metric.
vector, and we can
calculate the distance between arbitrarily chosen nodes based on shortest path
distance metric.
Strategies: a node’s
strategy means creating directed edges to the other nodes of the network. An
![]() player’s
strategy space
player’s
strategy space
![]() . Let s a given strategy vector:
. Let s a given strategy vector:
![]() . The union of the strategies completely determine the connectivity
graph in a given state:
. The union of the strategies completely determine the connectivity
graph in a given state:
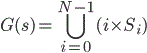 .
.
Payoff: every node has a cost function.
![]()
The goal of the players to minimize their own cost function, which consists of two parts. The first part is the communication cost (the summarized distance from other nodes) and the second part is network building cost (the summarized cost of the edges, which the node created).
For analyzing games, the following notations are used generally:
- Nash equilibrium (NE): this state means that no player has anything to gain by changing it’s strategy if the other nodes don’t change their strategy.
- Social optimum (SO): This state gives the cost of the optimal equilibrium meaning that the sum of the cost functions of the players are minimal, even if it is created with central coordination.
- Price of Anarchy: This shows the cost we may
pay for the lack of coordination in a worst-case scenario. It is calculated
as:
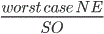
- Price of Stability: This shows the cost
that must be paid for reaching a stable state. It is calculated as:

My existing results
According to our assumption the reason behind the inefficiency of network formation in recovering complex networks as Nash equilibria is that they calculate the communication cost according to the length of the shortest paths, which seems to be unrealistic. For addressing this issue we have proposed Greedy Network Formation Game, in which we use greedy path-length for communication cost. We showed that the Kleinberg model - on which numerous routing algorithms are based - can’t emerge as a Nash equilibrium state, so it can’t exist in real world assuming constant dimensional Euclidean space.

Fig. 3: The distance between nodes with coordinate (2,2) and (0,0) according to greedy and shortest path in the case of a 2D Euclidean lattice
Our next step was redefining the game in hyperbolic space. The analysis of the game shows that this change is sufficient to get realistic scale-free networks as equilibrium state in a fairly natural manner.

Fig. 4: Equilibrium topology (left), in-degree distribution (center), out-degree distribution (right)
Impact and future research
Understanding the emergence of complex networks allows the prediction of numerous phenomena in a network. The greedy search based network solutions have several advantageous properties, they can operate well with local information in a distributed fashion, their fault tolerance is extremely high, their administration cost is low and furthermore, among proper conditions they can operate faster and simpler than current algorithms.
The analysis of the created games can serve as a ground for examining the effects of the BGP (Border Gateway Protocol) [8] for the topology of the Internet. The comparison of BGP with greedy and valley free routing [9] mechanism is also an interesting and current question.
My publications, references, link collection
My publications
[Sz1] Szabó, Dávid, “Önmagát szervező egyetemi hálózat” (in Hungarian), TDK essay, BME - VIK 2010, II. place
[Sz2] Szabó Dávid, Gulyás András, Csernai Márton, Heszberger Zalán, “Skálafüggetlen címzésen alapuló önszerveződő útvonalválasztási architektúra” (in Hungarian), Híradástechnika, 2011.
[Sz3] David Szabo, Marton Csernai, “Self organizing structureless routing architecture”, POSTER conference, 2011
[Sz4] Szabó Dávid, Gulyás András, “Jelterjedési utak topológiára gyakorolt hatásának vizsgálata játékelméleti módszerekkel” (in Hungarian), "Mesterpróba" Conference, 1. place, 2012
[Sz5] Andras Gulyas, Attila Korosi, Gergely Biczok, David Szabo, "On Greedy Network Formation", ACM SIGMETRICS W-PIN WS, 2012
[Sz6] Andras Gulyas, Attila Korosi, Gabor Retvari, Jozsef Biro, David Szabo, "Brief Announcement: Network Formation Games Can Give Rise to Realistic Network", PODC (Principles of Distributed Computing), 2012
[Sz7] Andras Gulyas, Attila Korosi, Gergely Biczok, David Szabo, "On Greedy Network Formation", to appear at ACM SIGMETRICS Performance Evaluation Review
References
[1] Erdös P. & Rényi, A. (1959) Publ. Math. 6 , 290-297
[2] D.J. Watts, P.S. Dodds, and M.E.J. Newman, “Identity and search in social networks”, Science, 296(5571):1302, 2002.
[3] Albert-László Barabási, Réka Albert, Hawoong Jeong, “Mean-field theory for scale-free random networks”, Physica A: Statistical Mechanics and its Applications, Volume 272, Issues 1-2, October 1999, Pages 173-187
[4] J. Travers and S. Milgram. An experimental study of the small world problem. Sociometry, 32:425–443, 1969.
[5] J. Kleinberg. The small-world phenomenon: an algorithm perspective. In Proc. of STOC’00, pages 163–170, 2000.
[6] Alex Fabricant, Ankur Luthra, Elitza Maneva, "On a Network Creation Game", PODC 2003, Pages 347-351
[7] Noam Nisan, “Algorithmic Game Theory”, 2007
[8] G. Huston, Analyzing the Internet's BGP routing table, potaroo.net, 2001, http://www.potaroo.net/papers/ipj/4-1-bgp.pdf
[9] Qiu, S.Y., Johns Hopkins, McDaniel, P.D., Monrose, F., "Toward Valley-Free Inter-domain Routing", Communications, 2007. ICC '07. IEEE International Conference, 2007
Link collection
Dept. of Telecommunications and Media Informatics
High Speed Network Laboratory (HSN Lab)
Watts and Strogatz small world model
