|
|
BMe Research Grant |
|
Doctoral School of Physics
Department of Physics/Institute of Physics
Supervisor: Dr. Dóra Balázs
Charge and Spin Dynamics in Low Dimensional Systems
Introducing the research area
I study various condensed matter systems driven far from equilibrium. The aim of my research is to understand the behaviour of quantum systems in the presence of perturbations that are turned on suddenly or gradually, and also under periodic driving. The main question is to give a comprehensive theoretical description of non-equilibrium dynamics, and also to characterize the stationary states that the systems reach after a long evolution.
Brief introduction of the research place
My PhD research has been carried out as a member of the BME-MTA Exotic Quantum Phases "Momentum" Research Group at the Department of Physics, Budapest University of Technology and Economics. The primary goal of the group is to study interacting quantum systems, exotic states of matter and non-equilibrium phenomena in the context of condensed matter physics.
Some of my topics have been investigated in collaboration with scientists from Dresden and Israel.
History and context of the research
Interest in non-equilibrium dynamics has grown immensely in the past few years thanks to experimental advances made with ultracold atomic gases [1]. The wide controllability of these systems allows experimentalists to prepare different kinds of non-equilibrium initial states and the dynamics can be studied with time resolution unreachable in other physical systems [2].
The most popular setups for non-equilibrium dynamics are quench experiments where the quantum system is driven out-of-equilibrium by suddenly switching on (or suddenly changing the magnitude of) an external electric or magnetic field (or even the interaction between the particles). The primary goal is to find and understand universal behaviour in non-equilibrium circumstances. For instance, it has been demonstrated that certain (interacting) systems forget the initial conditions after a long time and eventually reach a thermal state [3]. In contrast, other (non-interacting and some specially interacting) systems reach a qualitatively different steady state, which contains information about the initial conditions [4].
Similar universal features have been found in the short-term dynamics, for example the time evolution of various systems show singularities, which are dubbed dynamical phase transitions based on the analogy with thermal phase transitions [5].
Another vividly studied field is periodically driven systems. This type of perturbation can be used to engineer topological properties of matter. For example, normal insulators can be transformed into topological insulators by this method, which are promising candidates for applications in electronic devices.
1. figure Visualization of the studied non-equilibrium protocols
The research goal, open questions
1) Dynamical phase transitions:
The Loschmidt amplitude, which measures how close the time evolved state stays to the initial wave function, is a proper tool to characterize quench protocols. In certain one dimensional spin systems, dynamical phase transitions (singularities) were found in the Loschmidt amplitude if and only if the quench connected two different phases (e.g. when paramagnetic initial state is put in an environment that prefers ferromagnetic states, or vice versa). My investigations aimed to answer if these results can be generalized: can these singularities appear in quenches inside a given phase, can we observe similar phenomena in non-magnetic systems as well, and in higher dimensions?
2) Schwinger pair production:
The low energy excitations of some solid state systems exhibit relativistic dynamics, e.g. graphene, surfaces of topological insulators or Weyl semimetals [8]. A sudden switching on of an electric field creates particle-hole pairs in these materials, which is the condensed matter manifestation of the Schwinger mechanism [9], well-known from quantum electrodynamics. We were interested in the time evolution of the statistics of pair creation and of the current.
3) Periodically driven systems:
Periodic perturbations modify the band structure of solids, which is described in the framework of Floquet theory. Due to the violation of time translational symmetry, energy is not conserved, which has crucial consequences on the structure of Floquet-bands. It is not obvious how these bands are filled with electrons. It is often assumed in the literature that, similarly to the equilibrium case, at low temperatures the states with the lowest average energy are occupied. We wanted clarify how accurate this assumption is.
Methods
The large variety of the studied systems, circumstances and questions require various methods to be used during the research. A common link in all cases is that the time evolution is governed by the time dependent Schrödinger equation. Consequently, exact, approximate or numerical solutions of the Schrödinger equation should be found in order to determine various observables.
The primary aim was to find analytical results, because in a relatively new
field with lots of open questions, these provide more insight than
solving numerically some particular cases. The focus area is exactly
solvable systems, which, by a proper unitary transformation, can be
mapped to non-interacting problems. Such systems include 1D spin chains (Jordan-Wigner transformation), topological insulators and topological superconductors (Bogoliubov transformation).
In certain cases mappings can be used that transform time dependent problems to (approximately) time independent ones.
Exact results are not always available, or may be too complicated to enable a physical insight. In these cases, various approximations were applied including perturbation theory, Landau-Zener formula, etc. Validity of these approximations were supported by numerical solutions of the differential equations, or by other numerical methods, such as exact diagonalization.
Results
1) Dynamical phase transitions:
I found that singularities can also appear in quenches inside the paramagnetic or ferromagnetic phases in the XY quantum spin chain, so the conjecture that dynamical phase transitions may appear only for quenches connecting 2 separate phases was disproved. Applying Fisher's method [10], I was able to highlight a qualitative difference between dynamical phase transitions connecting two different phases, and those within the same phase [S3].
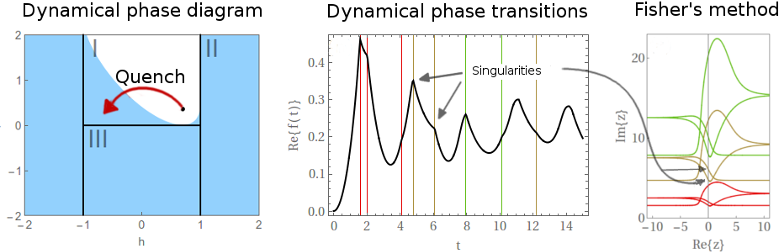
2. figure Domains of dynamical phase transitions (blue regions) on the equilibrium phase diagram, and the singularities of the time evolution appearing as kinks in the dynamical free energy.
I extended my studies to general two-band models. These include some previously studied spin models, but also normal and topological insulators and superconductors, which have not been investigated before. I proved that quenches connecting topologically different regions always imply dynamical phase transitions, and the difference between the two topological numbers give the number of non-equilibrium time scales. Also, this statement was extended to 2D systems, in which case the singularities appear in higher derivatives of the dynamical free energy, in analogy with second order phase transitions in equilibrium [S2].
2) Schwinger-pair creation:
The time evolution of the current and statistics of electron-hole pairs after switching on the electric field was determined. Interestingly, the current is a non-monotonic function of time with an initial quick increase of polarization current, followed by a power-law decay. Finally, due to the increasing number of particle-hole pairs moving in the same direction, the conduction current takes over the leading role, with the total current increasing again. An experimental observation of this non-monotonic current could serve as a signature of the Weyl semi-metal phase. The stationary conductivity of a disordered sample was also estimated from the dynamical picture, which agrees with other calculations in the literature in certain limits.
The statistics of electron-hole pairs changes from Poissonian for short perturbations to a Gaussian in the long perturbation regime [S1].
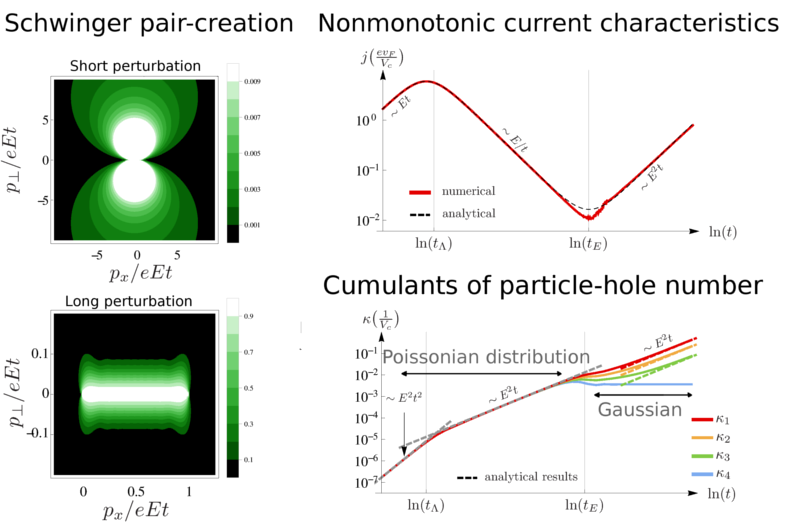
3. figure Momentum distribution of electron-hole pairs created by an electric field for a short and a long perturbation (left panel). Time evolution of the current and the cumulants (right panel).
3) Periodically driven systems:
On the particular example of a quantum spin-Hall insulator illuminated with circularly polarized light, the steady-state occupation of the Floquet bands was also investigated. It was shown that this occupation is not universal, i.e. it depends not only on the temperature of the environment (as one can expect in the static case), but also on the character of the external bath and on the quality of coupling to it. Although the naive picture, that the states with the lowest average energy are filled does not hold, the prediction that a circularly polarized light can induce a quantized current [6] stays valid.
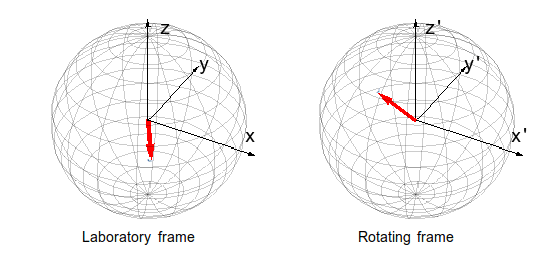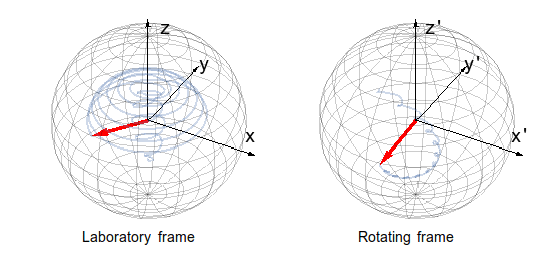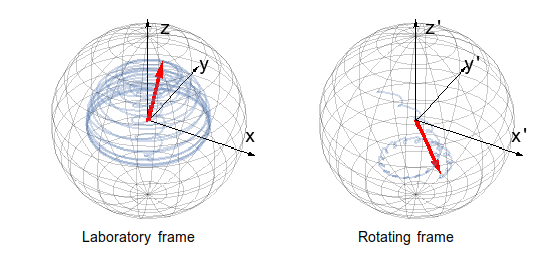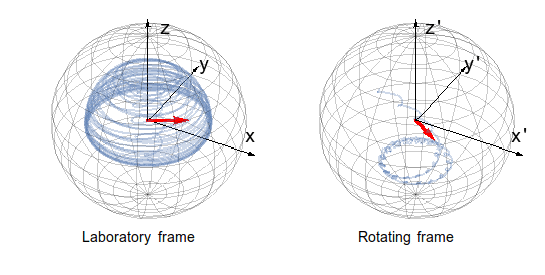
1. animation: Relaxation of a spin shined by circularly polarized light towards a non-equilibrium steady state. The complex motion in the laboratory frame is simplified in a properly chosen rotating frame.
Expected impact and further research
Our work has effectively contributed to the vivid field of non-equilibrium physics. My published results on dynamical phase transitions have received considerable scientific interest based on the 18 independent citations within a half year or one and a half years period [S2,S3], based on the NASA ADS data system. It is hoped that further results planned for publication in the near future will receive similar interest.
Additionally to solving some of the open questions in the topics described above, my aim is to find further connections between the non-equilibrium physics and topological properties of condensed matter.
Publications, references, links
Publications
[S1] Sz. Vajna, B. Dóra, R. Moessner, Non-equilibrium transport and statistics of Schwinger pair production in Weyl semimetals, arXiv:1505.08004 (2015) (submitted to PRB)
[S2] Sz. Vajna, B. Dóra, Topological classification of dynamical phase transitions, Physical Review B 91, 155127 (2015)
[S3] Sz. Vajna, B. Dóra, Disentangling dynamical phase transitions from equilibrium phase transitions, Physical Review B 89, 161105(R) (2014)
[S4] M. Vigh, L. Oroszlány, Sz. Vajna, P. San-Jose, Gy. Dávid, J. Cserti, B. Dóra, Diverging dc conductivity due to a flat band in disordered pseudospin-1 Dirac-Weyl fermions, Physical Review B 88, 161413(R) (2013)
[S5] Sz. Vajna, E. Simon, A. Szilva, K. Palotás, B. Ujfalussy, and L. Szunyogh, Higher-order contributions to the Rashba-Bychkov effect with application to the Bi/Ag(111) surface alloy, Physical Review B 85, 075404 (2012)
Links.
References.
[1] A. Polkovnikov, K. Sengupta, A. Silva, and M. Vengalattore, Rev. Mod. Phys. 83, 863 (2011).
[2] I. Bloch, J. Dalibard, and W. Zwerger, Rev. Mod. Phys. 80, 885 (2008).
[3] M. C. Banuls, J. I. Cirac, and M. B. Hastings, Phys. Rev. Lett. 106, 050405 (2011)
[4] M. Rigol, V. Dunjko, V. Yurovsky, and M. Olshanii, Phys. Rev. Lett. 98, 050405 (2007).
[5] M. Heyl, A. Polkovnikov, and S. Kehrein, Phys. Rev. Lett. 110, 135704 (2013).
[6] B. Dóra, J. Cayssol, F. Simon, R. Moessner, Phys. Rev. Lett. 108, 056602 (2012)
[7] C. Karrasch and D. Schuricht, Phys. Rev. B 87, 195104 (2013).
[8] A. A. Burkov and L. Balents, Phys. Rev. Lett. 107, 127205 (2011)
[9] J. Schwinger, Phys. Rev. 82, 664 (1951).
[10] M. E. Fisher, in Boulder Lectures in Theoretical Physics (University of Colorado, Boulder, 1965), Vol. 7.

