|
|
BMe Kutatói pályázat |
|
Fizikai Tudományok Doktori Iskola
BME TTK, Fizika Tanszék/Fizikai Intézet
Témavezető: Dr. Dóra Balázs
Töltés- és spin-dinamika alacsony dimenziós rendszerekben
A kutatási téma néhány soros bemutatása
Kutatómunkám során különféle szilárdtestfizikai rendszereket tanulmányozok egyensúlytól távoli körülmények között. A kutatás célja annak megértése, hogyan viselkednek kvantumos rendszerek folytonosan vagy hirtelen bekapcsolt, illetve periodikus zavarok jelenlétében. A perturbációt követő dinamika elméleti leírása mellett a fő kérdés a hosszú idő után kialakuló állandósult állapotok jellemzése.
A kutatóhely rövid bemutatása
Kutatásaimat a BME Fizika Tanszékén, illetve az MTA-BME Lendület Egzotikus Kvantumfázisok Kutatócsoportjában végzem. A csoport fő kutatási területe elméleti szilárdtestfizika, azon belül kölcsönható kvantum-rendszerek, egzotikus állapotok és nemegyensúlyi jelenségek leírása.
Kutatásaim egy része drezdai, ill. izraeli kutatókkal együttműködésben zajlik.
![]()
![]()
A kutatás történetének, tágabb kontextusának bemutatása
A nemegyensúlyi fizika iránti érdeklődés rendhagyó módon felélénkült az utóbbi évtizedben, elsősorban az ultrahideg atomi rendszerekhez kapcsolódó kísérleti technikák fejődésének köszönhetően [1]. Ezen rendszerek egyedülálló kontrollálhatósága lehetővé teszi különféle nemegyensúlyi állapotok preparálását, és a dinamika kísérleti tanulmányozását [2].
Az egyik legtöbbet tárgyalt nemegyensúlyi protokoll az úgynevezett kvencs, amikor a vizsgált rendszert úgy billentik ki az egyensúlyból, hogy a külső elektromos vagy mágneses teret (vagy akár a részecskék közötti kölcsönhatást) egyszeri alkalommal, hirtelen megváltoztatják. Az alapvető kérdés az, hogy különböző rendszerek mutatnak-e valamilyen univerzális viselkedést. Azt találták például, hogy bizonyos (kölcsönható) rendszerek a zavart követően hosszú idő után – elfelejtve a kezdeti állapotra vonatkozó információkat – egy véges hőmérséklettel jellemezhető állandósult állapotot érnek el [3], míg más (nem kölcsönható és néhány speciális kölcsönható) rendszerek egy kvalitatívan különböző – kezdeti feltételekre emlékező – állandósult állapotot érnek el [4].
A rövid távú dinamikában ugyancsak találtak univerzális viselkedést, például különféle rendszerekben az állapot időfejlődésében megfigyelhetők szingularitások, amit a fázisátalakulások analógiájára dinamikus fázisátalakulásoknak neveznek [5].
Egy másik aktívan kutatott terület az időben periodikus gerjesztések esete. Fontos jellemzőjük, hogy lehetőséget nyújtanak az egyensúlyi rendszert jellemző topologikus tulajdonságok megváltoztatására, például egy szokványos szigetelőt topologikus szigetelővé lehet így alakítani [6], amelyek sok előnyös tulajdonsággal rendelkeznek elektronikai alkalmazások szempontjából.
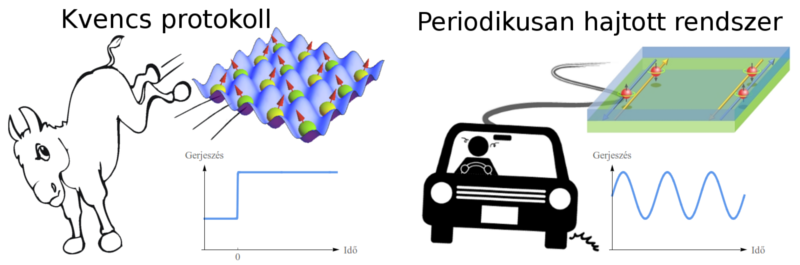
1.ábra Vizsgált nemegyensúlyi protokollok szemléltetése
A kutatás célja, a megválaszolandó kérdések.
1) Dinamikus fázisátalakulások:
A kvencset követő dinamika jól jellemezhető a Loschmidt amplitúdóval, amely azt méri, hogy a zavart követően az időfejlesztett hullámfüggvény mennyire tér el a kiinduló állapottól. Azt találták néhány egydimenziós mágneses rendszerben [5,7], hogy ha a kvencs két különböző fázist köt össze (például paramágnes kezdő állapotot ferromágneses állapotot preferáló körülmények közé helyezünk, vagy fordítva), a Loschmidt amplitúdó dinamikus fázisátalakulást mutat. Megvizsgáltam, hogy mennyire általánosíthatók ezek az eredmények: találhatunk-e hasonló szingularitásokat adott fázison belüli kvencs esetén, illetve hogy nem mágneses rendszerekben, vagy magasabb dimenzióban is láthatunk-e hasonló jelenséget.
2) Schwinger-párkeltés:
Egyes szilárdtestek alacsony energiás gerjesztési relativisztikus dinamikának engedelmeskednek (grafén, topologikus szigetelők felszíne, Weyl félfémek [8]). Ilyen esetben az elektromos teret hirtelen bekapcsolva (kvencs protokoll) elektron-lyuk párok keletkeznek, ami a kvantum-elektrodinamikából ismert Schwinger-mechanizmus [9] szilárdtestfizikai megfelelője. Itt a párkeltés statisztikájának, valamint a részecskék által képviselt áram időfejlődésére voltunk kíváncsiak.
3) Periodikusan hajtott rendszerek:
Időben periodikus gerjesztések hatására a szilárdtestek sávszerkezete megváltozik. Ennek leírására a Floquet elméletet használják, ami figyelembe veszi hogy az időeltolás-invariancia sérülése miatt az energia csak a gerjesztő frekvencia többszöröseinek erejéig marad meg. Nem nyilvánvaló, hogy ebben az esetben miként töltődnek be elektronokkal a szilárdtestek sávjai. Az irodalomban sokszor intuitívan azt feltételezik, hogy hideg környezetben a legalacsonyabb átlag-energiájú állapotok betöltöttek. Célunk pontosabb módszerekkel megvizsgálni, hogy mennyire helytálló ez a feltevés.
Módszerek
A kutatásaim során vizsgált rendszerek, a nemegyensúlyi körülmények, és a megválaszolandó kérdések széles spektruma többféle módszert igényelnek. Közös pont, hogy a dinamikát minden esetben az időfüggő Schrödinger egyenlet írja le, így ennek az egzakt, közelítő, vagy numerikus megoldásait használom a különféle vizsgált mennyiségek meghatározásához.
Elsősorban analitikus eredményekkel alátámasztott válaszokat keresek, amelyek a terület újdonságából adódó sok nyitott kérdés miatt mélyebb megértésre adnak lehetőséget, mint például az egy-egy konkrét, erősen kölcsönható rendszerre meghatározott numerikus adatok. Ezért egzaktul megoldható modelleket vizsgálok, amelyek valamilyen megfelelően választott unitér transzformáció segítségével nem-kölcsönható elméletekké képezhetők le. Ilyenek például az 1 dimenziós spin-láncok (Jordan-Wigner transzformáció), a topologikus szigetelők és a topologikus szupravezetők (Bogoliubov-transzformáció).
Bizonyos esetekben pedig olyan transzformációkat lehet alkalmazni, amelyek során az erősen időfüggő probléma egy (közelítőleg) időfüggetlen problémára képződik le.
Ahol az egzakt megoldás nem érhető el, vagy az eredmény bonyolultsága elfedi a mögöttes fizikát, perturbációszámítást, Landau-Zener átmeneti valószínűséget és más közelítéseket alkalmazok. Ezen közelítések jogosságát numerikus számításokkal támaszom alá, például differenciálegyenletek numerikus megoldásával vagy teljes diagonalizációval.
Eddigi eredmények
1) Dinamikus fázisátalakulások:
Cáfoltam az irodalomban megjelenő sejtést, miszerint dinamikus fázisátalakulást csak különböző egyensúlyi fázisokat összekötő kvencsek esetén találhatnánk. A legegyszerűbb ellenpéldát az XY spinláncot vizsgálva találtam, ahol mind a paramágneses, mind a ferromágneses fázison belüli kvencs esetén is megjelenhet szinguláris viselkedés. Fischer módszerét [10] alkalmazva kvalitatív különbséget találtam a fázison belüli és a két különböző fázist összekötő dinamikus fázisátalakulások között [S3].
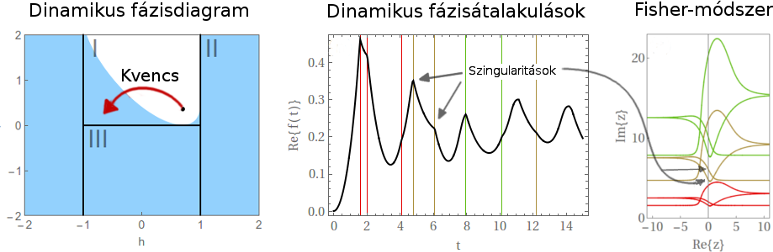
2.ábra Dinamikus fázisátalakulások tartománya (kék terület) az egyensúlyi fázisdiagramon, valamint a szingularitások megjelenése az időfejlődésben.
Kiterjesztettem vizsgálataimat általános kétsáv-modellekre, amelyeknek speciális eseteként előáll az irodalomban korábban vizsgált spin modellek egy része, emellett leírnak korábban nem vizsgált szigetelő, topologikus szigetelő, és szupravezető láncokat is. Bizonyítottam, hogy topológiailag különböző fázisok közötti kvencsek esetén mindenképpen megjelennek dinamikus fázisátalakulások, mégpedig annyi időskála megjelenésével, amennyi az egyensúlyi fázisokat jellemző topologikus szám megváltozása. Az eredményeket két dimenzióra is általánosítottam, ahol azt találtam, hogy szingularitás a dinamikus szabadenergia magasabb deriváltjában jelenik meg, analógiát mutatva az egyensúlyi magasabb rendű fázisátalakulásokkal [S2].
2) Schwinger-párkeltés:
Weyl-félfémekben meghatároztam az elektromos tér bekapcsolását követően az áram időfejlődését, és az elektron-lyuk párok számának statisztikáját. Érdekes módon az áram nem monoton függvénye az időnek, a bekapcsolást követő ultra-gyors válasz során az áram meredeken nő, majd egy hatványfüggvénnyel leírható csökkenésbe megy át, végül az egy irányba mozgó elektron-lyuk párok számának folyamatos növekedése miatt újból emelkedni kezd. A nem monoton áram kísérleti megfigyelése a Weyl-félfém fázis megvalósítását igazolhatná. Az időfüggő áram ismeretében megbecsültük egy szennyezett minta vezetőképességét, ami konzisztens eredményt adott az irodalomban fellelhető egyéb számolásokkal.
Az áram időfejlődésében megjelenő tartományokban a gerjesztések számának statisztikája is máshogy viselkedik: a rövid időkre jellemző Poisson statisztikából hosszú időkre jó közelítéssel Gauss-eloszlás fejlődik ki [S1].
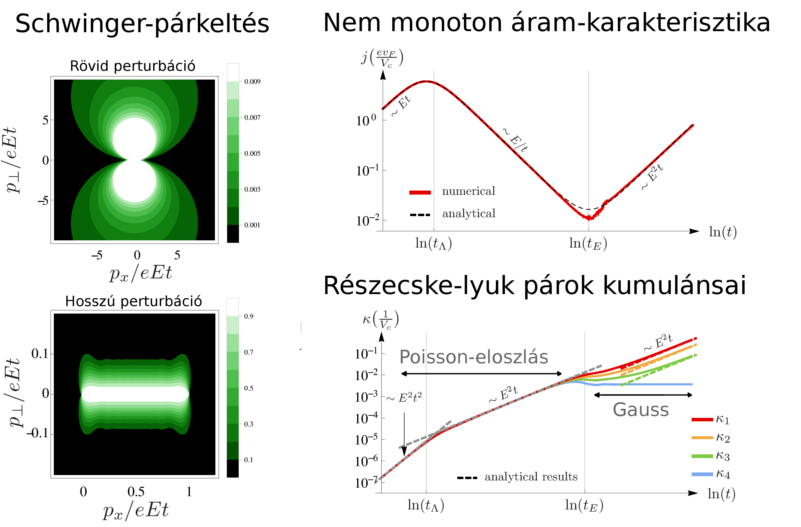
3. ábra Elektromos tér hatására keltett elektron-lyuk párok momentumtérbeli eloszlása rövid és hosszú időkre, valamint az áram és a kumulánsok időfejlődése.
3) Periodikusan hajtott rendszerek:
Cirkulárisan polarizált fénnyel megvilágított spin-Hall szigetelő élállapotainak speciális példáján keresztül vizsgálom, hogy a periodikusan hajtott rendszerekben hogyan töltődik be elektronokkal a módosult sávszerkezet. Megmutattuk, hogy ez a betöltődés nem univerzális, azaz nem csak a környezet hőmérsékletétől függ, mint ahogyan azt egyensúlyi rendszereknél megszokhattuk, hanem élesen befolyásolja a környezet és a környezettel való kölcsönhatás minősége is. Az átlagenergián alapuló betöltés tehát nem helytálló, viszont számolásaink alapján igaznak bizonyult a naiv modell azon jóslata, hogy a spin-Hall szigetelő élén kvantált áram folyik, ha cirkulárisan polarizált fénnyel világítjuk meg [6].
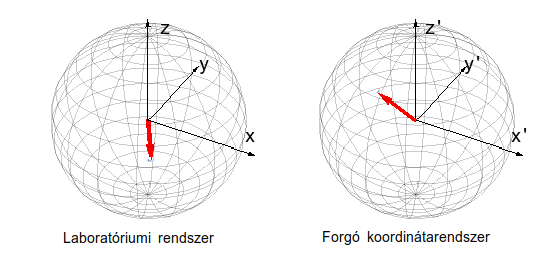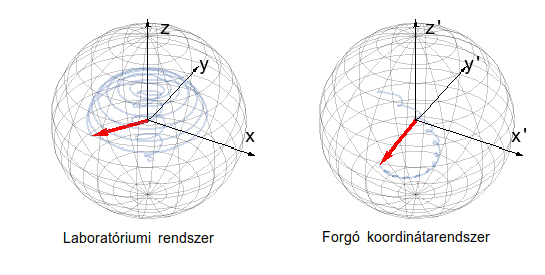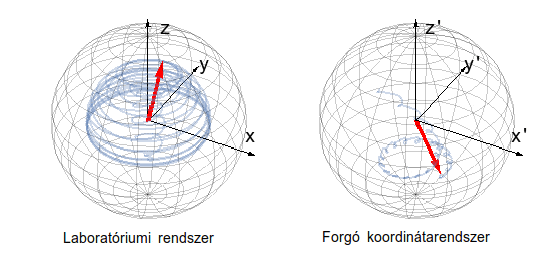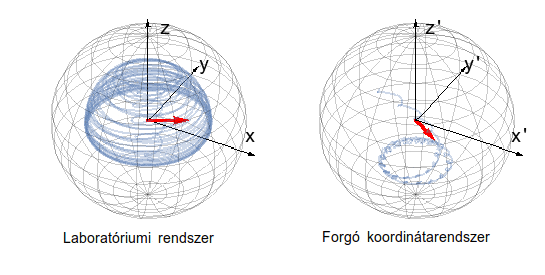
1. animáció: Cirkulárisan polarizált fénnyel megvilágított spin relaxációja egy nemegyensúlyi állandósult állapot felé. A laboratóriumi rendszerben látott összetett mozgás struktúrája leegyszerűsödik egy megfelelően választott forgó koordináta-rendszerből nézve.
Várható impakt, további kutatás
Kutatásainkkal hatékonyan bekapcsolódtunk a nemegyensúlyi fizika igen aktív nemzetközi mezőnyébe. Az eredményeimet rangos nemzetközi folyóiratokban publikáltuk, illetve tervezzük megjelentetni. A dinamikus fázisátalakulásokból írt cikkekre [S2,S3] a NASA ADS rendszer alapján kb. fél, ill. másfél év alatt összesen 18 független hivatkozás érkezett, reméljük a többi munkánkat is hasonló érdeklődés fogadja a jövőben.
A jövőben a fent bemutatott területeken nyitva maradt kérdések megválaszolásán túl célom további kapcsolatokat találni a rendszerek nemegyensúlyi viselkedése és topologikus tulajdonságai között.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája
[S1] Sz. Vajna, B. Dóra, R. Moessner, Nonequilibrium transport and statistics of Schwinger pair production in Weyl semimetals, arXiv:1505.08004 (2015) (submitted to PRB)
[S2] Sz. Vajna, B. Dóra, Topological classification of dynamical phase transitions, Physical Review B 91, 155127 (2015)
[S3] Sz. Vajna, B. Dóra, Disentangling dynamical phase transitions from equilibrium phase transitions, Physical Review B 89, 161105(R) (2014)
[S4] M. Vigh, L. Oroszlány, Sz. Vajna, P. San-Jose, Gy. Dávid, J. Cserti, B. Dóra, Diverging dc conductivity due to a flat band in disordered pseudospin-1 Dirac-Weyl fermions, Physical Review B 88, 161413(R) (2013)
[S5] Sz. Vajna, E. Simon, A. Szilva, K. Palotás, B. Ujfalussy, and L. Szunyogh, Higher-order contributions to the Rashba-Bychkov effect with application to the Bi/Ag(111) surface alloy, Physical Review B 85, 075404 (2012)
Linkgyűjtemény
Hivatkozások listája
[1] A. Polkovnikov, K. Sengupta, A. Silva, and M. Vengalattore, Rev. Mod. Phys. 83, 863 (2011).
[2] I. Bloch, J. Dalibard, and W. Zwerger, Rev. Mod. Phys. 80, 885 (2008).
[3] M. C. Banuls, J. I. Cirac, and M. B. Hastings, Phys. Rev. Lett. 106, 050405 (2011)
[4] M. Rigol, V. Dunjko, V. Yurovsky, and M. Olshanii, Phys. Rev. Lett. 98, 050405 (2007).
[5] M. Heyl, A. Polkovnikov, and S. Kehrein, Phys. Rev. Lett. 110, 135704 (2013).
[6] B. Dóra, J. Cayssol, F. Simon, R. Moessner, Phys. Rev. Lett. 108, 056602 (2012)
[7] C. Karrasch and D. Schuricht, Phys. Rev. B 87, 195104 (2013).
[8] A. A. Burkov and L. Balents, Phys. Rev. Lett. 107, 127205 (2011)
[9] J. Schwinger, Phys. Rev. 82, 664 (1951).
[10] M. E. Fisher, in Boulder Lectures in Theoretical Physics (University of Colorado, Boulder, 1965), Vol. 7.
