|
|
BMe Research Grant |
|
Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering
BME GPK, Department of Applied Mechanics
Supervisor: Dr. Stépán Gábor
Dynamics of Dual-point Rolling Bodies
Introducing the research area
Investigated mechanical systems which contain a body being in dual-point contact with another body, and both rolling and slipping can occur between their surfaces. The research topic arose from two engineering applications (vibrations of railway wheelsets and dynamics of a special type of flowmeter). However, I also aimed at better understanding of the various phenomena caused by the Coulomb-friction in three-dimensional contact of bodies.
Brief introduction of the research place
My research work is connected to the Department of Applied Mechanics. The department is involved in high-level research activities in various fields of applied mechanics, such as machine tool vibrations, wheel dynamics, dynamics of robots, balancing and continuum mechanics. In recent years, members of the department took part in several international research projects. The department also hosts the Dynamics of Machines and Vehicles Research Group.
History and context of the research
In railway vehicles, there is no differential gear, but the wheels of the wheelset are connected rigidly to each other. The possibility of rolling between the rails and both wheels is ensured by the slightly conical shape of wheels. Then, in the curvatures of the track, there will be difference between the rolling radii of the wheels (Fig. 1).
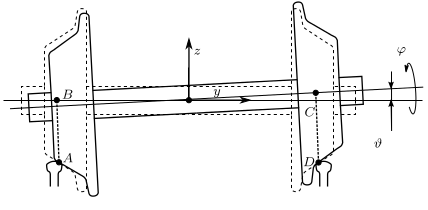
Figure 1: Location of the railway wheelset in the curvature of the track. The rolling radii (distances AB and CD) are different. Source: [A1].
However, the conical profile can cause vibrations in the presence of external disturbances. These vibrations can also occur on a straight track (Fig. 2), and they reduce not only the comfort level of the railway vehicle but the lifetime of the parts.
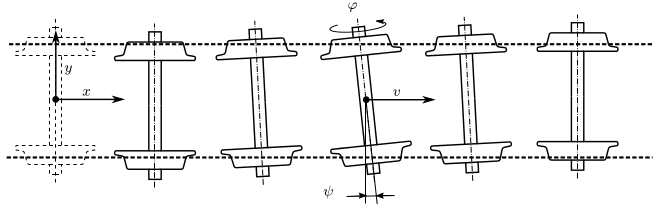
Figure 2: Kinematic oscillation of a railway wheelset. Source: [A1].
In case of rolling, the frequency of the vibrations was determined by Klingel back in the 19th century [R1]. But due to the deformations in the vicinity of the contact points, the motion of the wheelset slightly deviates from rolling (phenomenon of creep), which effect was taken into account first by Carter [R2]. From that model, the critical velocity where vibrations appear can be calculated. Since then, many analytic and numeric models has been developed [R3,R4], but open questions still exist due to the complexity of the system.
The kinematic connection between the railway wheelset and the rails is very similar to that in a special type of flowmeter called orbital ball flowmeter (Fig. 3). The construction of this device is described in several patents (see e.g. [R5,R6]). The work principle of this flowmeter is as follows: the fluid flow makes a ball to roll along the edge of the measuring vessel, and the motion of the ball could be used to determine the flow rate. These type of flowmeters however, do not work properly in practice, and the reasons have not been investigated from dynamical point of view as yet.
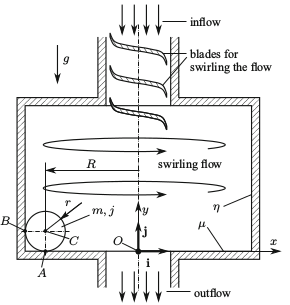
Figure 3: Sketch of the orbital ball flowmeter. Source: [A4].
Research goals, open questions
In the mentioned engineering applications, the moving part (the wheelset and the ball) touches the standing part at two contact points and both rolling or slipping can occur at each point.
If case of rolling at both contact points of the railway wheelset we speak of the phenomenon of the so-called kinematic oscillation. The frequency of these oscillations depends not only on the velocity of the vehicle and the geometry of the rail and wheel profiles, but also on the amplitude of the oscillation. One main goal of my research work was to construct the analytical formulae on this dependence by considering the nonlinearities from the 3D motion and the shape of profile curves.
Both at the wheelset and at the orbital ball flowmeter, we are interested in the conditions of slipping at one or both contact points. By considering Coulomb-friction, one should calculate the constraint forces at the contact point, and the condition of slipping would be determined by checking the maximum admissible static friction force. However, contact forces cannot be calculated uniquely at dual-point rolling, that is, condition of slipping cannot be determined. The question is how can we resolve this indeterminacy and when will the slipping occur.
Answering this question can be applied to the two engineering problems presented above. What explanation can the Coulomb-friction give to the calibration problems of the orbital ball flowmeter? What dynamical effects arise if we model the railway wheelset by Coulomb-friction?
Methods
During the research work, I applied analytical methods to find answers to the above questions. However, numerical methods were also applied for checking and visualizing.
The railway wheelset has the 6 degrees of freedom of a rigid body, 2 degrees of freedom are fixed by the contact with the rails, and 3 degrees of freedom are restricted by the rolling constraint. If the speed of the railway vehicle is given then all degrees of freedom of the wheelset is prescribed and the differential equation of the motion is determined purely by kinematics. Due to the complicated geometry of the 3D surfaces of the bodies, the location of the contact points are also considered as variables, then, constraints of the dual-point contact can be written as implicit functions. If the profile curves of the rail and the wheel are given, then the contact points have a neutral location on the surfaces (see Fig. 4). Around this equilibrium state, the power series of the profile curves are calculated up to the fourth order terms to obtain the approximate nonlinear differential equations. Then, the dependence of frequency on the amplitude can be determined by the theory of nonlinear vibrations.
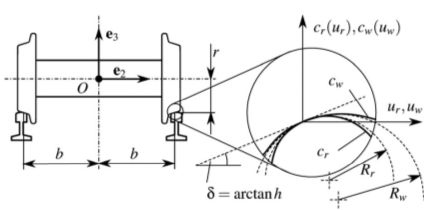
Figure 4: The railway wheelset in neutral position on a straight track. In the figure, the profile curves are denoted by cr and cw. Source: [A3].
In the 2D case, the theory of Filippov-type non-smooth systems could be applied to the problem of slipping [R7]. In the 2D case of the Coulomb-friction, there is a jump in the friction force when the velocity of the contact point changes sign (see e.g. Fig. 5). The dynamics corresponding to the two directions of sliding results in a non-smooth dynamical system. Then, analysis of the differential equation shows whether the rolling body starts slipping permanently of the slipping system returns to rolling from both directions. For that, one have to determine the so-called sliding and crossing states of the system.
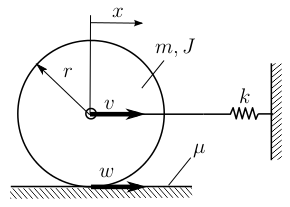
Figure 5: A simple mechanical system to demonstrate the methods of Filippov systems. The two directions of slipping and the rolling creates the non-smooth behavior of the system. Source: [A9].
However, Coulomb-friction results in a more complicated non-smooth system at 3D contact of bodies. It is not the two types of dynamics (slipping right or left) that describes the system, but the contact point can slip to directions of the plane, which results continuously in many different values of the friction force. These systems are not covered by the Filippov's theorem. Therefore, I extended the Filippov systems to codimension-2 discontinuity sets, which mathematical description includes the 3D contact of bodies with Coulomb-friction.
At dual-point rolling, the extended methods can be used separately at both contact points to determine the condition of slipping. Essentially, the method requires taking the limit of the acceleration from all possible directions. The method is applicable effectively both for the railway wheelset and the orbital ball flowmeter.
Results
I succeeded in deriving the nonlinear differential equation up to the third order terms for arbitrary profiles, and the full nonlinear differential equation for the purely conical wheel profile. These equations cannot be found in the literature. I showed that the linearized formula of Meijaard [R8] is valid for small vibrations even if the curvature of the profiles is not constant. I showed that the frequency of finite amplitude oscillations differs from the linear frequency in a term which is proportional to the square of the amplitude. I derived the effect of the geometry on the increase or decrease of frequency with the increasing amplitude (Fig. 6). The resulting formulae show that the change of frequency is mostly caused by the first derivative of the curvatures. Therefore, the change of frequency can be sensitive to the change of profile curves during wear. Corresponding publications: [A1],[A1],[A3].
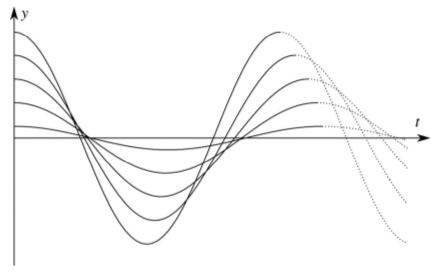
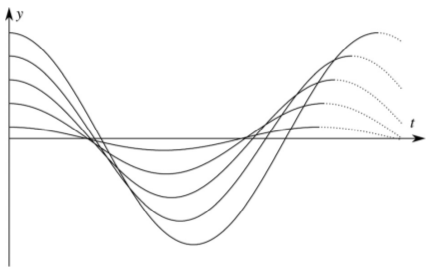
Figure 6: Time history of the kinematic oscillation in the cases when the increasing amplitude increases (left) or decreases (right) the frequency. Source: [A3].
Analysis of the orbital ball flowmeter showed that slipping of the ball occurs at one of the contact points and also at both contact points. Moreover, in some cases the ball can even rise from the bottom of the measuring vessel, and it can roll on the wall of the vessel. I determined the bifurcation diagrams of the system, which can be used to recognize the effects of the different parameters on the possible kinds of behaviors (Fig. 7). It was revealed that the proper operation of the device is deteriorated by several effects: the significant lag of the ball at dual-point slipping, the huge hysteresis which makes calibration almost impossible and the transient states of the ball entailing impacts. Corresponding publications: [A4],[A5],[A6].


Figure 7: Bifurcation diagrams of the orbital ball flowmeter. Source:[A4].
Analysis of dual-point slipping of the railway wheelset showed that in case of large amplitude oscillations, the Coulomb model provides an appropriate approximation of the widely used nonlinear creep model (see Fig. 8). An interesting feature is, however, that in the case of Coulomb model, no unique critical vehicle speed exists. Instead, we get a maximal velocity depending on the amplitude where the dual-point rolling can still arise. (Fig. 9) From the current results, it seems that in the physically relevant parameter range, the dual-point slipping is more typical than slipping at one of the contact points. Corresponding publications: [A7],[A8].
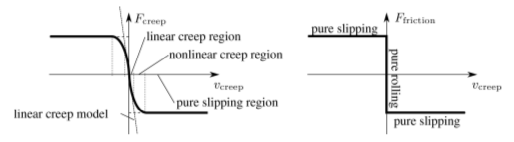
Figure 8: Comparison of the characteristic curves of the widely used nonlinear creep model (left) and the Coulomb model (right). Source:[A7].
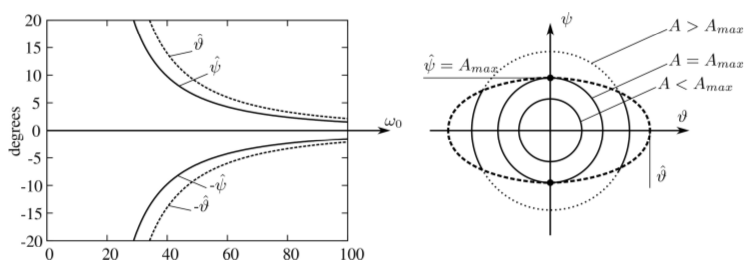
Figure 9: Maximal amplitudes depending on the velocity. At these boundaries, there is still no slipping. Source: [A7].
When extending the Filippov systems, I succeeded to generalize several definitions and results to the codimension-2 discontinuity manifolds. Publication of these results which belong to the field of applied mathematics is still in process. Corresponding publications: [A9],[A10],[A11].
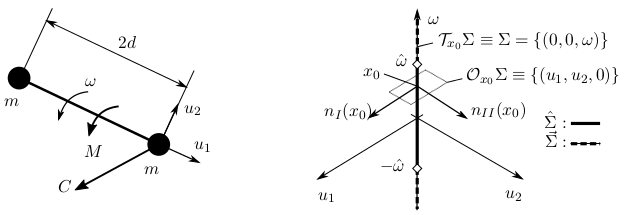
Figure 10: Simple mechanical system to demonstrate the theory of codimension-2 discontinuity sets. The two mass points in the plane are connected by a rod and one of the mass points is subject to Coulomb friction. Source: [A10].
Expected impact and further research
The obtained results allow a deeper understanding of the behavior of the two presented engineering systems. Moreover, we obtained formulae of the effects of different parameters. The methods used can be applied to other systems containing dual-point rolling, e.g. in the case of roller bearings.
When describing the railway wheelset by Coulomb friction, several open questions remained which can be the topic of further research work. Additionally to the effect of slipping, e.g. investigation of the properties of periodic solution that possibly occur can also be important.
There are several unfinished details about the extension of Filippov systems, that can be explored by further research. These results can help applying the approaches and notions learned from the Filippov systems to 3D contact problems.
Publications, references, links
List of corresponding own publications
[A1] Antali, M., Stépán, G., Hogan, S.J.: Kinematic oscillations of railway wheelsets. Multi-body Syst. Dyn. 34(3) pp. 259–275, 2015. (IF=1.74)
[A2] Antali, M., Stépán, G.: Nonlinear kinematic oscillations of railway wheelsets of general surface geometry. Proc. Appl. Math. Mech. 14(1) pp. 303–304, 2014.
[A3] Antali, M., Stépán, G.: On the nonlinear kinematic oscillations of railway wheelsets. J. Comput. Nonlin. Dyn. 11(5) pp. 1–10. 2016 (in press) (IF=1.14)
[A4] Antali, M., Stépán, G.: Discontinuity-induced bifurcations of a dual-point contact ball. Nonlin. Dynam. 83(1) pp. 685–702, 2016. (IF=3.00)
[A5] Antali, M., Stépán, G.: Nonlinear dynamics of a dual-point-contact ball. Proceedings of 8th European Nonlinear Dynamics Conference (ENOC 2014), Paper no. 478, pp. 1–2, 2014.
[A6] Antali, M., Stépán, G.: Két ponton gördülő golyó nem-folytonos dinamikája (in Hungarian). Proceedings of Twelft Hungarian Conference of Mechanics (MAMEK 2015), Paper no. 215, pp. 1–8, 2015.
[A7] Antali, M., Stépán, G.: Loss of stability in a non-smooth model of dual-point rolling. The Dynamics of Vehicles on Roads and Tracks pp. 937–946, 2016.
[A8] Antali, M., Stépán, G.: Oscillations of railway wheelsets with discontinuous model of the contact forces, Sixth International Conference on Nonlinear Vibrations, Localization and Energy Transfer (ICNV 2016), (accepted for publication)
[A9] Antali, M., Stépán, G.: Non-smooth analysis of a simple rolling-sliding mechanical system with Coulomb friction. Investigating Dynamics in Engineering and Applied Science (IDEAS 2014), Paper no. 21, 1 p, 2014
[A10] Antali, M., Stépán, G.: Sliding dynamics on codimension-2 discontinuity surfaces, Trends in Mathematics: Non-smooth Dynamics, pp. 1–4., 2016 (in press)
[A11] Antali, M., Stépán, G.: Sliding dynamics on isolated codimension-2 discontinuity manifolds (under publication)
Collection of links
Properties of railway wheelsets (Wikipedia)
Oscillations of railway wheelsets (Wikipedia)
History of rail transportation (Wikipedia)
Brief overview of non-smooth dynamical systems (Twelfth)
References
[R1] Klingel, J.: Uber den Lauf von Eisenbahnwagen auf gerader Bahn.
Organ Fortschr. Eisenbahnwes. 38, pp. 113–123, 1883
[R2] Carter, F. W.: On the Action of a Locomotive Driving Wheel. Proc. R. Soc. 112(760), pp. 151–157. 1926
[R3] Iwnicki, S.: Simulation of Wheel-Rail Contact Forces,” Fatigue Fract. Eng. Mater. Struct. 26(10), pp. 887–900, 2003
[R4] Wickens, A. H.: Fundamentals of Rail Vehicle Dynamics: Guidance and Stability. Swets and Zeitlinger, Lisse, The Netherlands, 2003
[R5] Eldridge, G., Eldridge, R.: Cyclonic Flow Meters, US Patent,
US 5 905 200, 1999
[R6] Peters, M.L.J.P.: Orbital Ball Flowmeter for Gas and Fluids,
US Patent, US 8 505 378 B2, 2013
[R7] di Bernardo, M., Budd, C.J., Champneys, A.R., Kowalczyk,
P.: Piecewise-Smooth Dynamical Systems. Springer, Berlin, 2008
[R8] Meijaard, J. P.: Kinematic analysis of a wheelset as an aid to understanding and modifying the postcritical behaviour. Proceedings of 8th European Nonlinear Dynamics Conference (ENOC 2014), Paper no. 134, pp. 1–2, 2014
