Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola   

BME GPK, Műszaki Mechanikai Tanszék

Témavezető: Dr. Stépán Gábor

Két ponton gördülő testek dinamikája

A kutatási téma néhány soros bemutatása

Kutatásom során olyan mechanikai rendszereket vizsgáltam, ahol az egyik test két ponton érintkezik a másikkal, és a felületek között gördülés és csúszás is létrejöhet. A kutatási téma két konkrét gépészeti probléma vizsgálatából indult (vasúti kerekek rezgése, illetve golyós fogyasztásmérő  működése), de cél volt annak mélyebb megértése is, hogy a Coulomb-súrlódás milyen jelenségeket okoz a testek mozgásában térbeli érintkezés esetén.

 

A kutatóhely rövid bemutatása

A kutatást a Műszaki Mechanikai Tanszéken végeztem. A tanszéken nemzetközileg elismert kutatási tevékenység folyik számos alkalmazott mechanikai területen, mint a szerszámgéprezgések, kerékdinamika, robotok mechanikája, egyensúlyozás és kontinuum-mechanika. A tanszék dolgozói az elmúlt években több nemzetközi kutatási projektbe is bekapcsolódtak. A tanszékkel összefonódva működik a Gépek és Járművek Dinamikája Kutatócsoport.

 

A kutatás történetének, tágabb kontextusának bemutatása

A vasúti járművekben nem alkalmaznak differenciálművet, hanem a kerék-pár a tengelyen keresztül mereven kapcsolódik. Ezért a vasúti kerekek enyhén kúpos geometriája biztosítja a gördülő kapcsolat lehetőségét a sínek és mindkét kerék között, mivel kanyarban a kerekek gördülő sugarai között különbség jön létre (1. ábra).

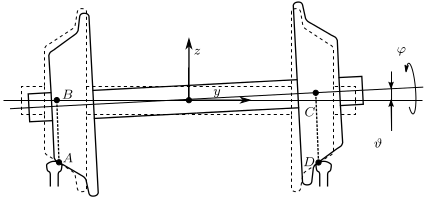
1. ábra: A vasúti kerék-pár elhelyezkedése kanyarban. A gördülő körök sugarai (AB és CD távolságok) különbözőek. Forrás: [A1].

 

A kúpos profil azonban zavarás hatására rezgésekhez vezethet, mely egyenes pályán is bekövetkezhet (2. ábra), és amely nem csak a vasúti jármű konfortszintjét, hanem az alkatrészek élettartamát is csökkenti.

2. ábra: A vasúti kerék-pár kinematikai rezgése. Forrás: [A1].

 

A gördülés közben kialakuló rezgés frekvenciáját Klingel már a XIX. század végén meghatározta [R1]. Az érintkezési pontok környezetében fellépő deformációk miatt azonban a mozgás kissé eltér a gördüléstől (kúszás jelensége). Ezt a hatást először Carter vette figyelembe [R2]. A modellből kiszámítható volt, hogy a vasúti jármű milyen sebességénél jelennek meg a rezgések. Azóta számos analitikus és numerikus módszert fejlesztettek ki a kerék rezgéseinek leírására [R3,R4], de a rendszer bonyolultsága miatt számos nyitott kérdés maradt.

 

A sínnel érintkező vasúti kerék-pár esetéhez nagyon hasonló kinematikai kapcsolatot találunk a golyós áramlásmérő konstrukciójában (3. ábra), mely több tucatnyi szabadalomban megtalálható (lásd pl. [R5,R6]). Az ötlet lényege, hogy a folyadékáram által a hengeres mérőtér éle mentén körbejáró golyó mozgásából meghatározható lenne a folyadékáram mértéke. Ezek az áramlásmérők a gyakorlatban nem működnek megfelelően, melynek dinamikai hátterét korábban még nem vizsgálták.

 

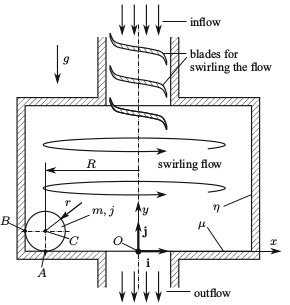
3. ábra: A golyós áramlásmérő vázlatos felépítése. Forrás: [A4].

 

A kutatás célja, a megválaszolandó kérdések

A fenti gépészeti rendszerekben a mozgó alkatrész – a kerék-pár illetve a golyó – két ponton érintkezik az álló alkatrésszel és mindkét érintkezési pontban létrejöhet gördülés vagy megcsúszás.

 

Ha vasúti kerék-pár esetében mindkét érintkezési pontban gördülés lép fel, az úgynevezett kinematikai rezgés jelenségét tapasztaljuk. A kialakuló rezgések frekvenciája a vasúti jármű sebessége mellett a kerék- és sínprofilok geometriájától és a rezgés amplitúdójától is függ. A kutatás egyik célja ezen összefüggések analitikus előállítása a profilokból és a térbeli mozgásból származó nemlinearitások figyelembevételével.

 

A vasúti kerekek és a golyós áramlásmérő esetén is felmerülő kérdés, hogy milyen feltételek mellett következik be megcsúszás egyik vagy mindkét érintkezési pontban. Ha Coulomb-súrlódást feltételezünk, ki kellene számítani az érintkezési pontban fellépő kényszererőket, és megcsúszás akkor következne be, ha a maximálisan megengedettnél nagyobb tapadási súrlódási erő adódna. Azonban kétpontos gördülés esetén a kényszererők nem számíthatók ki egyértelműen, így a megcsúszás feltétele sem határozható meg. Felmerülő kérdés, hogy hogyan oldható fel ez a bizonytalanság, és mikor fog bekövetkezni a megcsúszás? 

 

Ezen kérdés megválaszolása után a két gépészeti problémára is visszatérhetünk. Milyen magyarázatot adhat a Coulomb-súrlódás a golyós áramlásmérő kalibrációs problémáira? Milyen dinamikai hatásokhoz vezet, ha a vasúti kerekek esetén is Coulomb-féle súrlódást feltételezünk?

 

Módszerek

A kérdésekre analitikus számításokkal kerestem a választ, az ellenőrzésre és szemléltetésre azonban numerikus módszereket is igénybe vettem.

 

A vasúti kerék-párnak mint merev testnek 6 szabadsági foka van, amelyből a sínnel való érintkezés feltétele 2, míg a kétpontos gördülés 3 szabadsági fokot köt meg. Ha a vasúti jármű sebességét is adottnak tekintjük, akkor a kerék minden szabadságfoka kötött lesz, és a mozgást leíró differenciálegyenletet kizárólag kinematikai összefüggések határozzák meg. A térbeli felületek bonyolult geometriája miatt a test kinematikai jellemzői mellett az érintkezési pontok pozícióját is változókkal írjuk le, így implicit formában felírhatók a kétpontos érintkezés kényszerfeltételei. Ha adott kerék- és sínprofilok esetén a kerék rezgés nélkül mozog, akkor az érintkezési pontoknak van egy természetes elhelyezkedése a felületeken (4. ábra). Ezen egyensúlyi állapot körül a profilgörbéket negyedrendben, a térbeli mozgást pedig harmadrendben sorba fejtve megkaphatók a közelítő nemlineáris differenciálegyenletek. Ezután a nemlineáris rezgések elméletének segítségével határozhatjuk meg a frekvencia függését az amplitúdótól.

4. ábra: A vasúti kerék-pár egyensúlyi helyzetben egyenes sínpálya esetén. Az ábrán cr és cw jelöli a profilgörbéket. Forrás: [A3].

 

Síkbeli esetben a megcsúszási problémához a Filippov-féle nem-sima dinamikai rendszerek matematikai elmélete lenne alkalmazható [R7]. A Coulomb-súrlódás síkbeli esetében az érintkezési pont sebességének előjelváltásakor a súrlódási erő ugrásszerűen megváltozik (lásd pl. 5. ábra). A kétféle irányú csúszás dinamikája együtt nem-sima dinamikai rendszerhez vezet. Ekkor eldönthető a differenciálegyenlet vizsgálatával, hogy a gördülő mozgás kis csúsztató zavarás hatására tartósan valamelyik irányban csúszni kezd-e, vagy a megcsúszó rendszer bármely irányból visszatér-e a gördülő állapotba. Ehhez az úgynevezett csúszó (sliding) és áthaladó (crossing) állapotokat kell meghatározni.

 

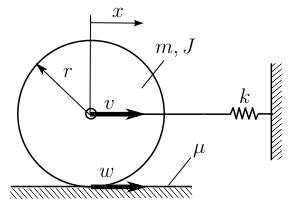
5. ábra: Egyszerű mechanikai rendszer a Filippov-rendszerek módszereinek bemutatására. A korong jobbra vagy balra csúszhat, valamint gördülhet; ez adja a nem-sima dinamikát. Forrás: [A9].

 

Térbeli érintkezéskor azonban a Coulomb-súrlódás bonyolultabb nem-sima dinamikai rendszerre vezet. Nem kétféle dinamika írja le a rendszert (balra, illetve jobbra csúszik), hanem az érintkezési pont a sík bármely irányába megcsúszhat, minden irányban más súrlódási erőt eredményezve. Az ilyen rendszereket nem lehet kezelni a Filippov-elmélet segítségével. Ezért a kutatás során kiterjesztettem a Filippov-rendszereket 2 kodimenziós nem-folytonossági sokaságokra, amely matematikai leírás tartalmazza a két test térbeli érintkezésekor fellépő Coulomb-súrlódást is.

 

A kétpontos gördüléskor a két érintkezési pontban külön-külön vizsgálhatjuk meg a kifejlesztett elmélet segítségével, hogy bekövetkezik-e a megcsúszás. Ehhez lényegében az érintkezési pont gyorsulásának határértékét kell vennünk az összes lehetséges megcsúszási irányból nézve. A módszer alkalmazása a vasúti kerék és a golyós áramlásmérő esetén eredményesen alkalmazható.

 

Eddigi eredmények

Sikerült levezetni tetszőleges profil esetére a vasúti kerék harmadfokig sorba fejtett differenciálegyenletét, valamint tisztán kúpos kerékprofil esetére a teljes differenciálegyenletet, melyek nem találhatók meg a szakirodalomban. Megmutattam, hogy a Meijaard által közölt [R8] linearizált formula kis rezgések esetén akkor is helyesen megadja a kinematikai rezgések frekvenciáját, ha a profilgörbék görbülete nem állandó. Megmutattam, hogy a véges amplitúdójú rezgések frekvenciája a lineáris frekvenciától az amplitúdó második hatványával arányosan tér el. Levezettem, hogy a geometria miként határozza meg, hogy a frekvencia csökken vagy nő az amplitúdó növekedésével (6. ábra). A formulákból kiderült, hogy a frekvencia változását leginkább a profilgörbék görbületének első deriváltja okozza. Emiatt a profilok kopás következtében bekövetkező megváltozása érzékenyen befolyásolhatja a rezgések frekvenciáját. Kapcsolódó publikációk: [A1],[A2],[A3].

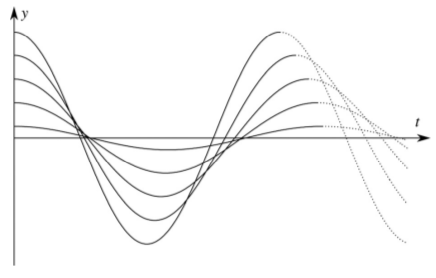
6. ábra: A kinematikai rezgés időfüggése, ha az amplitúdó növekedése növeli (balra), illetve csökkenti (jobbra) a frekvenciát. Forrás: [A3].

 

A golyós áramlásmérő vizsgálatánál kiderült, hogy egyik vagy mindkét érintkezési pontban bekövetkezhet a golyó megcsúszása. Ráadásul bizonyos esetekben a golyó akár felemelkedhet a mérőedény aljáról, és tartósan gördülhet a fal mentén. Meghatároztam a rendszer bifurkációs diagramjait, melyekről leolvasható, hogy a paraméterek változtatása esetén milyen jellegű viselkedés jön létre (7. ábra). Kiderült, hogy a mérőműszer működését több jelenség is elrontja: a golyó kétpontos megcsúszáskor történő jelentős lemaradása az áramláshoz képest, a kalibrációt megnehezítő jelentős hiszterézis és a golyó ütközésekkel is járó átmeneti állapotai. Kapcsolódó publikációk: [A4],[A5],[A6].

 

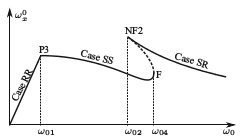
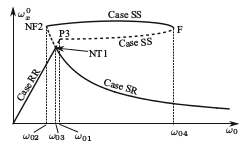
7. ábra: A golyós áramlásmérő bifurkációs diagramjai. Forrás: [A4].

 

A vasúti kerék két pontos megcsúszását vizsgálva kiderült, hogy nagy amplitúdójú rezgések esetén a Coulomb-modell megfelelő közelítését adja a szakirodalomban elterjedt nemlineáris kúszási modelleknek (8. ábra). Érdekesség viszont, hogy a Coulomb-modell esetében nem adódik ki egyértelmű kritikus sebesség. Kiszámítható viszont az amplitúdótól függő maximális sebesség, ahol a kétpontos gördülés még létrejöhet (9. ábra). Az eddigi eredmények szerint úgy tűnik, hogy a fizikailag valós paramétertartományban a két ponton történő egyidejű megcsúszás előbb következik be, mint az egyik érintkezési pontban történő megcsúszás. Kapcsolódó publikációk: [A7],[A8].

 

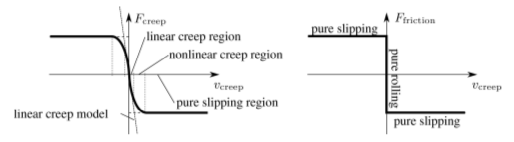
8. ábra: A szakirodalomban elterjedt nemlineáris kúszási modell (balra) és a Coulomb-modell (jobbra) összehasonlítása. Forrás: [A7].

 

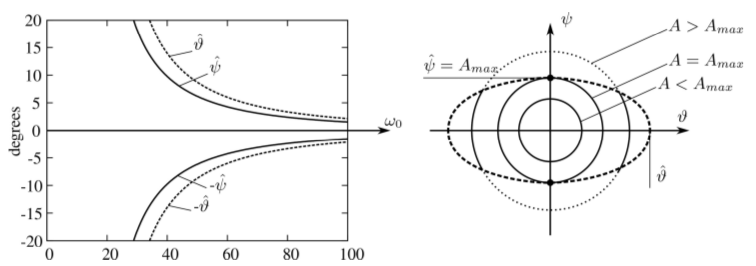
9. ábra: A sebességtől függő maximális amplitúdók alakulása, ameddig nem jön létre megcsúszás. Forrás: [A7].

 

A Filippov-rendszerek kiterjesztésekor sikerült számos definíciót és eredményt általánosítani a két kodimenziós nem-folytonosságok esetére. Az alkalmazott matematika területéhez tartozó eredmények folyóiratcikkben történő publikálása jelenleg folyamatban van. Kapcsolódó publikációk: [A9],[A10],[A11].

 

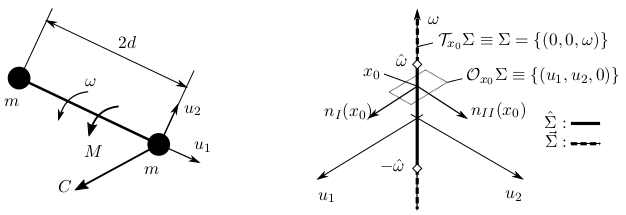
10. ábra: Egyszerű mechanikai rendszer, melyre alkalmazható a 2 kodimenziós nem-folytonossági sokaságok elmélete. A rúddal összekötött két tömegpont a síkon mozog, az egyikre Coulomb-súrlódás hat. Jobbra a fázistér vázlata látható. Forrás: [A10].

 

Várható impakt, további kutatás

A kapott eredmények segítenek mélyebben megérteni a két vizsgált gépészeti rendszer viselkedését, valamint formulákat is kaptunk a paraméterek hatásaival kapcsolatban. A használt módszerek alkalmazhatók lehetnek más olyan rendszereknél is, ahol a kétpontos gördülés előfordul, így például a gördülőcsapágyak esetében.

 

A vasúti kerék Coulomb-súrlódással való leírásakor számos megválaszolatlan kérdés van, melyek a további kutatás témáját képezik. A megcsúszás határa mellett fontos lehet például vizsgálni az esetlegesen kialakuló periodikus megoldások tulajdonságait.

 

A Filippov-rendszerek kiterjesztésével kapcsolatban még sok részletkérdés maradt, melyeket a későbbi kutatásban fel lehetne térképezni. Ezen eredmények segítségével a Filippov rendszerekből ismert szemléletet és fogalmakat alkalmazhatjuk a térbeli érintkezési problémákra is.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

 

[A1] Antali, M., Stépán, G., Hogan, S.J.: Kinematic oscillations of railway wheelsets. Multibody Syst. Dyn. 34(3) pp. 259–275, 2015. (IF=1.74)

 

[A2] Antali, M., Stépán, G.: Nonlinear kinematic oscillations of railway wheelsets of general surface geometry. Proc. Appl. Math. Mech. 14(1) pp. 303–304, 2014.  

 

[A3] Antali, M., Stépán, G.: On the nonlinear kinematic oscillations of railway wheelsets. J. Comput. Nonlin. Dyn. 11(5) pp. 1–10. 2016 (megjelenés alatt) (IF=1.14)

 

[A4] Antali, M., Stépán, G.: Discontinuity-induced bifurcations of a dual-point contact ball. Nonlin. Dynam. 83(1) pp. 685–702, 2016. (IF=3.00)

 

[A5] Antali, M., Stépán, G.: Nonlinear dynamics of a dual-point-contact ball. Proceedings of 8th European Nonlinear Dynamics Conference (ENOC 2014), Paper no. 478, pp. 1–2, 2014.

 

[A6] Antali, M., Stépán, G.: Két ponton gördülő golyó nem-folytonos dinamikája. Proceedings of Twelft Hungarian Conference of Mechanics (MAMEK 2015), Paper no. 215, pp. 1–8, 2015.

 

[A7] Antali, M., Stépán, G.: Loss of stability in a nonsmooth model of dual-point rolling. The Dynamics of Vehicles on Roads and Tracks pp. 937–946, 2016.

 

[A8] Antali, M., Stépán, G.: Oscillations of railway wheelsets with discontinuous model of the contact forces, Sixth International Conference on Nonlinear Vibrations, Localization and Energy Transfer (ICNV 2016), (elfogadva)

 

[A9] Antali, M., Stépán, G.: Nonsmooth analysis of a simple rolling-sliding mechanical system with Coulomb friction. Investigating Dynamics in Engineering and Applied Science (IDEAS 2014), Paper no. 21, 1 p, 2014

 

[A10] Antali, M., Stépán, G.: Sliding dynamics on codimension-2 discontinuity surfaces, Trends in Mathematics: Nonsmooth Dynamics, pp. 1–4., 2016 (megjelenés alatt)

 

[A11] Antali, M., Stépán, G.: Sliding dynamics on isolated codimension-2 discontinuity manifolds (publikálás alatt)

 

Linkgyűjtemény.

 

Vasúti kerekek tulajdonságai (Wikipédia, angol)

Vasúti kerekek rezgései (Wikipédia, angol)

Vasúti közlekedés története (Wikipédia, angol)

Nem-sima dinamikai rendszerek áttekintése (Scholarpedia, angol)

 

Hivatkozások listája.

 

[R1] Klingel, J.: Uber den Lauf von Eisenbahnwagen auf gerader Bahn.

Organ Fortschr. Eisenbahnwes. 38, pp. 113–123, 1883

 

[R2] Carter, F. W.: On the Action of a Locomotive Driving Wheel.  Proc. R. Soc. 112(760), pp. 151–157. 1926

 

[R3] Iwnicki, S.: Simulation of Wheel-Rail Contact Forces,” Fatigue Fract. Eng. Mater. Struct. 26(10), pp. 887–900, 2003

 

[R4] Wickens, A. H.: Fundamentals of Rail Vehicle Dynamics: Guidance and Stability. Swets and Zeitlinger, Lisse, The Netherlands, 2003

 

[R5] Eldridge, G., Eldridge, R.: Cyclonic Flow Meters, US Patent,

US 5 905 200, 1999

 

[R6] Peters, M.L.J.P.: Orbital Ball Flowmeter for Gas and Fluids,

US Patent, US 8 505 378 B2, 2013

 

[R7] di Bernardo, M., Budd, C.J., Champneys, A.R., Kowalczyk,

P.: Piecewise-Smooth Dynamical Systems. Springer, Berlin, 2008

 

[R8] Meijaard, J. P.: Kinematic analysis of a wheelset as an aid to understanding and modifying the postcritical behaviour. Proceedings of 8th European Nonlinear Dynamics Conference (ENOC 2014), Paper no. 134, pp. 1–2, 2014