|
|
BMe Research Grant |
|
George A. Olah Doctoral School of Chemistry and Chemical Technology
Department of Inorganic and Analytical Chemistry
Supervisor: Dr. Csonka Gábor István
3D Quantum Chemical Modeling of Biomolecules
Introducing the research area
The aim of my doctoral research is developing and applying theoretical chemistry methods based on the three-dimensional electron density (density functionals) for the examination of the spatial structure and weak interactions of biomolecules. In my work, I apply my recently developed highly accurate method in two biologically exceptionally important recognition processes: in immune recognition and epigenetic recognition.
Brief introduction of the research place
There is a many-decade history of theoretical chemical research at the Department of Inorganic and Analytical Chemistry (BUTE) in several groups. The department gave many researchers and teachers to the scientific community, who accomplished significant achievements. My supervisor has several highly-cited (ISI citation classic) publications in the field of theoretical physical chemistry [1-9] (one is over 1800 citations). He has widespread international liaisons, and he is an adjunct professor at Tulane University and Temple University in the USA.
History and context of the research
My research is based on my supervisors' previous research started with Prof. Imre Csizmadia in 1995, in which they examined the potential energy surface of carbohydrates and glycopeptides with computational chemistry methods. The computed sugar conformers and energies were included in one of the most popular quantum chemical benchmark database (GMTKN30) as the SCONF test set.
With my essay written from my research started as an MSc student, I won the 1st prize at the Institutional Scientific Students’ Conference. During my PhD work, we extended our research to another biologically significant process, in which the methylated DNA is epigenetically recognized by different proteins. The implications of this topic is pictured by the fact that in 2015, a 32 page long paper with 95 authors was published in Nature about the analysis of the full human epigenome.
Nowadays, the computer science reached a level of development where the accurate quantum chemical computation of larger biological systems is becoming available. My newly developed dRPA75 method is related to this. My method can accurately and efficiently provide the interaction energy of a system comprising about 100 main-group elements.
The research goals, open questions
O-glycosylation in the immune recognition
The structure and interactions of proteins are influenced not only by their amino acid sequence but also by their post-translational modifications. The sugar units linked to the side chain oxygen atom of serine or threonine amino acids are called the O-glycosylation. Such protein modifications are present in cancer cells in the Tn antigen. However, in healthy cells, the immune system has anti body against the Tn antigen, which can suppress the production of the Tn antigen. In immune recognition, possibly the sugar antenna encodes the information on the surface of the protein. Interesting questions are: what sort of sugar units can bind to the protein surface, in which orientation, and how does it influence the protein structure?
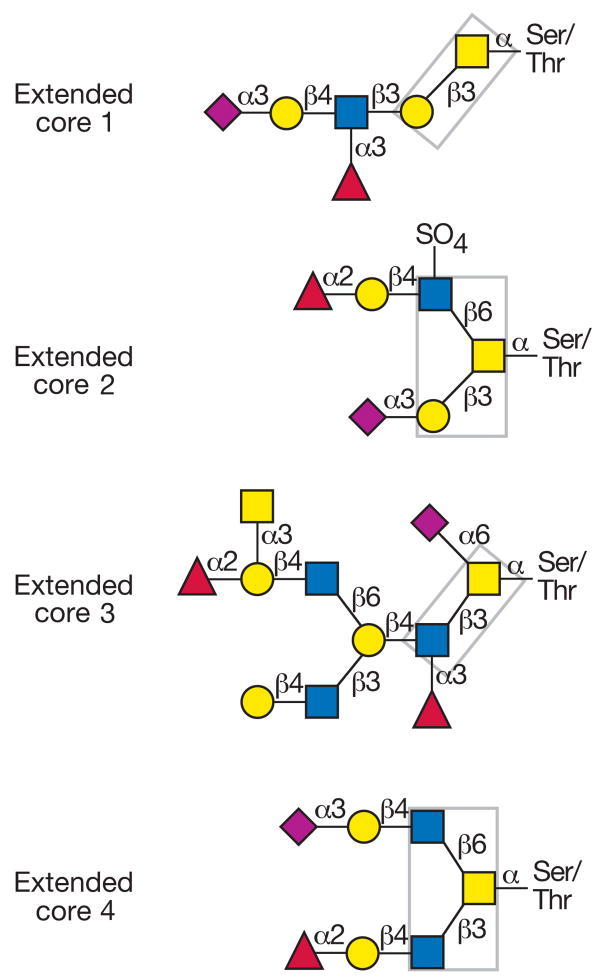
Fig. 1 Possible core structures of the O-glycosidic sugar antenna
(yellow circle = galactose; yellow square = N-acetylgalactosamine; blue square = N-acetylglucosamine; purple rhomb = N-acetylneuraminic acid; red triangle = fucose)
DNA methylation in the epigenetic recognition
In addition to the genetic information, DNA contains also epigenetic information, which regulates the gene expression. This information is usually provided by the symmetric methylation of the cytosines of the palindromic cytidine-phosphate-guanosine dinucleotide (CpG) motifs in the promoter region of the genes. This alters the interaction surface of the DNA major groove. Thus methyl-CpG-binding domain (MBD) proteins bind to the methylated DNA, which leads to transcriptional repression. For the suppression of DNA damages formed during the DNA synthesis or by environmental effects, the organisms have various repair mechanisms. The alteration of the DNA methylation pattern can cause the transcriptional repression of the tumor suppressor genes, which can lead to cancer. Interesting questions are: what sort of interactions determine the methyl-DNA recognition, and what kind of mechanism drives it?
Fig. 2 Symmetrically methylated CpG motif in DNA
Methods
Density functional theory
Density functional theory [10] handles the physical systems as hypothetical non-interacting systems with an effective potential. This theory is efficient because we use simple one-electron orbitals for the many-particle wave function. The hypothetical system gives an electron density identical to the physical one, and gives the exact electron energy. The only flaw here is that the universal form of the effective potential is unknown, hence approximations are needed during the application of the theory.
Density functional approximations
Among the density functional approximations [11] the lowest rung considers the non-homogeneous electron densities of the physical systems as a homogeneous electron gas. This is a good approximation for metal lattices with slowly varying densities, but for the rapidly varying densities of atoms and molecules corrections are needed, to take into account the density changes as well. An even greater challenge is the description of the long-range weak interactions among the molecules because these interactions have a purely non-local nature, so knowing local electron densities is not sufficient.
My method for weak interactions
The dRPA75 method developed by myself [S4] can efficiently consider the non-local interactions. It provides highly accurate energies (0.2–0.5 kcal/mol accuracy) for the weak interactions inside (intramolecular) and among (intermolecular) the biomolecules. Furthermore, it performs well for the reaction energies and activation energies of organic molecules. My method can be efficiently implemented in computer codes. [12, 13]
Other methods
For the approximate calculation of the interaction energy, I applied the second-order perturbative MP2 method. For the quick optimization of molecule geometries, I applied the semi-local M06L density functional method. For the sake of more accurate frequencies in the thermochemical computations, I optimized the geometries with the hybrid B3LYP density functional method. For the calculations, I used different triple split valence basis sets.
Results
Intramolecular interactions in immune recognition
I investigated the structure and energetics of the O-glycosidic linkage on serine model structures substituted by α and β N-acetylgalactosamine and N-acetylmannosamine. According to the previous gas-phase model structures, the hydrogen bonding pattern on the N-acetylgalactosamine sugar unit can fix the position of the acetamido group, when the (O3)H group forms a hydrogen bond with the O7 atom. However, I have shown that the (O4)H group forms a hydrogen bond with the O6 atom in a similar arrangement, the (O3)H group can turn towards the O4 atom allowing the acetamido group to rotate. Furthermore, the rotation is also allowed, if the (O3)H group is substituted in the sugar antenna.

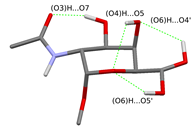
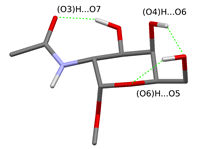
Fig. 3 Possible hydrogen bonding patterns on the sugar unit fixing the acetamido group
(The rotational isomers differing only in the orientation of the (O6)H group are shown in the same figure.)
It was assumed by the earlier gas-phase structures that the acetamido group on the sugar unit directly attaches to the glycopeptide backbone stiffening the structure of the glycopeptide linkage. However, I have shown that adding a single water molecule to the system, the structural water molecule can build in between the rotatable acetamido group of the sugar unit and the peptide backbone. This allows the breaking of the hydrogen bond which stiffens the peptide backbone and alters the prefered γ-turn secondary structure of the peptide chain.
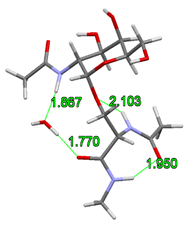
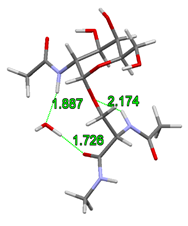
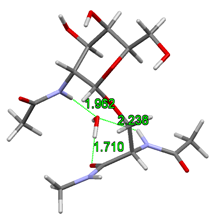
Fig. 4 Building of structural water into the glycopeptide linkage
According to the gas-phase structures, the rigidity of glycopeptide linkage is the highest for the α isomers and for the N-acetylgalactosamine. Furthermore, I have shown that instead of the previously assumed γ-turn secondary structure, the building in of the structural water molecule allows also the formation of the polyproline II helix and the antiparallel β-chains secondary structures. The computed torsion angles agree better with the experimentally determined torsion angles. Their variations in a broader range together with the large space filling of the sugar antenna agree better with the formation of the experimentally observed random loops.
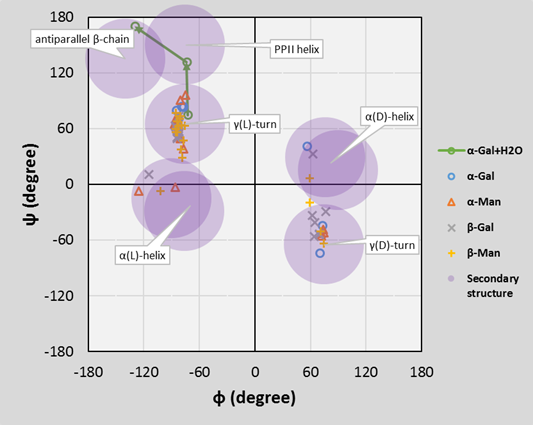
Fig. 5 Ramachandran diagram for the O-glycopeptide backbone
Intermolecular interactions in the epigenetic recognition
Firstly, I examined the interactions between the methyl-DNA and MBD proteins using two smaller arginine-guanine-methylcytosine model triads. The observed interaction types were the following: hydrogen bonding between the arginine and guanine; cation-π interaction between the methylcytosine and the arginine; and dispersion interaction between the methyl group of the methylcytosine and the arginine side chain. The strength of these interactions increased during the geometry optimization with the increasing flexibility of the arginine side chain, the DNA major groove, and the protein’s peptide backbone, respectively. The computed strength of the interactions is: -42–43 kcal/mol per triads. From this, the impact of a single methyl group means a -1–2 kcal/mol stabilization, and this effect is more significant in case of the arginine 44.

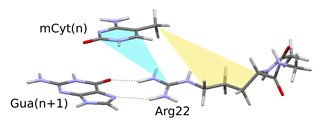
Fig. 6 Possible interactions between the methylated DNA and the MBD protein
For the thermochemical computations at room temperature I used a larger model, which contained two arginine side chains, one aspartate side chain and two cytosine and two guanine bases closed by methyl groups. Each model with varying number of structural water molecules showed -42 kcal/mol Gibbs energy change. In the calculated interaction, the large negative entropic term dominates, which suggests the central role of the hydrophobic interaction.
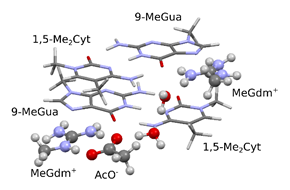
Fig. 7 Model for the interaction between the methyl-CpG motif and MBD protein
The rigid helical rotation of the side chains of the MBD protein along the DNA double helix shows that during the sliding of the protein, the arginine side chains would approach differently the methyl groups of the neighboring methylcytosines above or under the plane of the guanidinium groups. The diagram shows that the arginine 22 side chain means a sterical hindrance for the sliding of the protein towards one direction because the aspartate side chain fixes its position by hydrogen bonds and blocks its rotation (locked state). At the same time, the arginine 44 side chain means a sterical hindrance for the sliding towards the other direction only if it forms two hydrogen bonds with the guanine (open/closed states). This statement agrees well with the experimentally observed "hopping" scanning mechanism of the MBD4 protein.
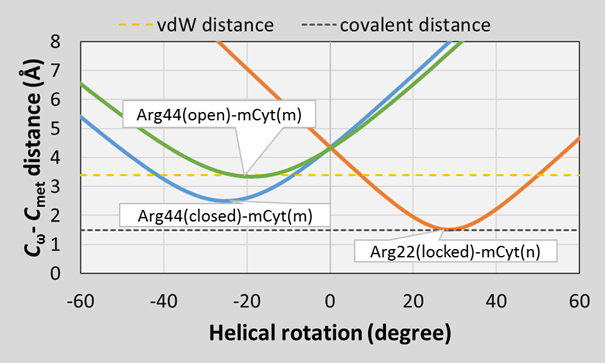
Fig. 8 Steric hindrances for the helical rotation of the MBD proteins on the DNA double helix
Expected impact and further research
Four of my papers [O1–8] were published in the Journal of Chemical Theory and Computation (IF: 5,498), which belongs to the first 10% in the field of theoretical chemistry. Last fall, I had the honor to be a Research Scholar in the Center for Materials Theory at Temple University (USA).
My dRPA75 theoretical method shows an excellent performance in many fields of molecular physical chemistry. This is well represented by the fact that this method was implemented into the MRCC quantum chemistry software shortly after its development.
My model for the effect of the O-glycosylation on the protein structure agrees better with the experimental observations for the local and global structure of glycoproteins than the previous models.
My model for the interaction surface of the methyl-CpG motif and the MBD proteins can serve as basis to understand deeper the mechanism of the methyl-DNA recognition.
Publications, references, links
Publications:
[O1] Mezei, P. D.; Csonka, G. I.; Ruzsinszky, A.; Sun, J. J. Chem. Theory Comput. 2015,
11, 360–371. (IF = 5.498, CT = 6)
[O2] Mezei, P. D.; Csonka, G. I.; Kállay, M. J. Chem. Theory Comput. 2015, 11, 2879–2888.
(IF = 5.498, CT =3)
[O3] Mezei, P. D.; Csonka, G. I.; Ruzsinszky, A. J. Chem. Theory Comput. 2015, 11,
3961–3967. (IF = 5.498, CT = 3)
[O4] Mezei, P. D.; Csonka, G. I.; Ruzsinszky, A.; Kállay, M. J. Chem. Theory Comput.
2015, 11, 4615–4626. (IF = 5.498, CT = 6)
[O5] Perdew, J. P.; Sun, J.; Ruzsinszky, A.; Mezei, P. D.; Csonka, G. I. Period. Polytech.
Chem. Eng. 2016, 60, 2–7. (IF = 0.296, CT =2)
[O6] Mezei, P. D.; Csonka, G. I. Struct. Chem. 2015, 26, 1367–1379. (IF = 1.837)
[O7] Mezei, P. D.; Csonka, G. I. Struct. Chem. 2016, STUC-D-16-00037R1 (accepted).
(IF = 1.837)
[O8] Mezei, P. D.; Ruzsinszky, A.; Csonka, G. I. J. Chem. Theory Comput. 2016,
ct-2016-00-323c (under revision). (IF = 5.498)
Links:
References:
[1] Perdew, J.; Ruzsinszky, A.; Csonka, G. I.; Vydrov, O.; Scuseria, G.; Constantin, L.; Zhou, X.; Burke, K. Phys. Rev. Lett. 2008, 100, 136406.
[2] Ruzsinszky, A.; Csonka, G. I.; Scuseria, G. E. J. Chem. Theory Comput. 2009, 5, 763–769.
[3] Perdew, J. P.; Ruzsinszky, A.; Csonka, G. I.; Constantin, L. A.; Sun, J. Phys. Rev. Lett. 2009, 103, 026403.
[4] Ruzsinszky, A.; Sun, J.; Xiao, B.; Csonka, G. I. J. Chem. Theory Comput. 2012, 8, 2078–2087.
[5] Perdew, J. P.; Ruzsinszky, A.; Tao, J.; Staroverov, V. N.; Scuseria, G. E.; Csonka, G. I. J. Chem. Phys. 2005, 123, 62201.
[6] Steinmann, S. N.; Csonka, G. I.; Corminboeuf, C. J. Chem. Theory Comput. 2009, 5, 2950–2958.
[7] Ruzsinszky, A.; Perdew, J. P.; Csonka, G. I. J. Chem. Theory Comput. 2010, 6, 127–134.
[8] Ruzsinszky, A.; Perdew, J. P.; Csonka, G. I. J. Chem. Phys. 2011, 134, 114110.
[9] Csonka, G. I.; French, A. D.; Johnson, G. P.; Stortz, C. A. J. Chem. Theory Comput. 2009, 5, 679–692.
[10] Kohn, W.; Sham, L. J. Phys. Rev. 1965, 140, A1133–A1138.
[11] Perdew, J. P.; Schmidt, K. AIP Conf. Proc. 2001, 577, 1–20.
[12] Heßelmann, A. Phys. Rev. A 2012, 85, 012517.
[13] Rolik, Z.; Szegedy, L.; Ladjánszki, I.; Ladóczki, B.; Kállay, M. J. Chem. Phys. 2013, 139, 094105.
