|
|
BMe Kutatói pályázat |
|
Villamosmérnöki Tudományok Doktori Iskola
BME VIK, Méréstechnika és Információs Rendszerek Tanszék
Témavezető: Dr. Kollár István
Robusztus Least Squares szinuszillesztés
A kutatási téma néhány soros bemutatása
A számítógépek elterjedésével a jelfeldolgozási feladatok túlnyomórészt digitálisan valósulnak meg, környező világunk jelei azonban analóg formában állnak rendelkezésre. A két oldal közötti átjárást az analóg-digitális (A/D) átalakítók biztosítják. Mivel számos sorozatgyártásba kerülő termék (pl. autóipari termékek, mobiltelefonok) tartalmaz A/D átalakítókat, az elvégzendő tesztek száma is jelentős. Ennek következtében kritikus fontosságú, hogy a teszteket numerikusan stabilan tudjuk végrehajtani. Kutatásom célja az A/D-átalakítók teszteléséhez szükséges szinuszillesztő algoritmusok numerikus kiértékelés szempontjából érzékeny pontjainak felderítése, valamint a tesztelés robusztus kiértékelésének biztosítása.
A kutatóhely rövid bemutatása
Kutatásaimat a Méréstechnika és Információs Rendszerek Tanszéken végzem a Digitális Jelfeldolgozás Laboratórium támogatásával. A Tanszéken egy A/D-átalakítókkal foglalkozó háromfős kutatócsoport munkájában veszek részt Dr. Kollár István irányítása alatt [L1].
A kutatás történetének, tágabb kontextusának bemutatása
Kutatásaim során szinuszillesztő algoritmusok vizsgálatával foglalkozom, különös hangsúlyt fektetve azok numerikus tulajdonságaira. Ezen algoritmusok használatára a villamosmérnöki tudomány számos területen szükség van. Szinuszos jellel lehet jellemezni például a villamosenergia-rendszer szolgáltatási minőségét. Ezen kívül mivel szinuszos jelet nagy pontossággal lehet előállítani, ilyen típusú gerjesztést ír elő az analóg-digitális átalakítók, valamint a digitális hullámforma-generátorok tesztelésére létrehozott szabvány (IEEE 1241, ill. IEEE 1057), [6],[7]. Ahhoz, hogy mérőszámot tudjunk adni ezen szolgáltatások minőségére, szükség van arra, hogy a szinuszos jel paramétereit pontosan tudjuk becsülni. A legelterjedtebben használt módszer a legkisebb négyzetes hibát minimalizáló Least Squares (LS) szinuszillesztés. Ezt definiálják a fent említett szabványok is. Az algoritmus robusztus, gyors és könnyen programozható, azonban numerikus szempontból több ponton is jelentősen javítható a teljesítménye [1]–[3],[S1].
A kutatás célja, a megválaszolandó kérdések
Egy mintavételezett szinuszos jelet a következőképpen írhatunk le:
![]()
ahol yk a mintavételezett jel k-dik eleme, tk pedig a k-dik mintavételi időpont, A, B és C a jel koszinuszos, szinuszos és egyenkomponensének amplitúdói, f pedig a jel frekvenciája. Általában egyenletes mintavételezést alkalmazunk a következő mintavételi időpontokkal:
![]()
ahol fs a mintavételi frekvencia, N pedig a mintavett regisztrátum hossza. Ekkor
![]()
Egy szinuszos jel jellemzéséhez az alábbi négy paraméterre van szükség:
A, B,
C és f/fs. A paraméterek becsléséhez [6] Least Squares megoldást ír elő. A megoldás egyszerűsítése érdekében
f/fs helyett
![]() -et becsüljük, ahol
-et becsüljük, ahol
![]() a körfrekvenciát jelöli. A megoldandó egyenletrendszer tehát:
a körfrekvenciát jelöli. A megoldandó egyenletrendszer tehát:
vagyis
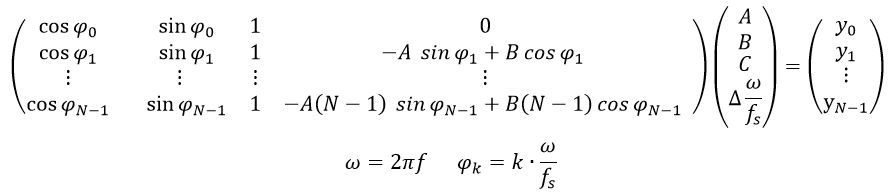
Ebből az egyenletből jól látszik, hogy míg D első, második és harmadik oszlopában az elemek -1 és 1 közötti értékeket vehetnek fel, addig a negyedik oszlop elemeinek abszolút értékei a mintaszám növekedtével folyamatosan nőnek. A probléma matematikai megfogalmazásához a kondíciószám fogalmára van szükség. A kondíciószám jelen esetben DTD legnagyobb és legkisebb szinguláris értékének hányadosa, mely felülről korlátozza a Least Squares megoldás hibáját. Minél nagyobb a kondíciószám, annál érzékenyebb a megoldás kis (például kerekítési hibákból adódó [1]) perturbációkra. Amennyiben például a kondíciószámot a felére tudjuk csökkenteni, úgy az egyenletrendszer megoldásaként adódó paraméterek maximális relatív hibája szintén a felére csökken. Mivel a kondíciószám egy arányszám, ezért nem csökkenthető 1 alá, így ez az ideális kondíciószám. Hogy szemléltessük az 1 kondíciószám numerikusan kedvező voltát, megjegyezzük, hogy tetszőleges méretű egységmátrixnak 1 a kondíciószáma.
A kutatási területen ismert [8], hogy a négyparaméteres Least Squares módszer rosszul kondicionált feladat. Ennek illusztrálására tekintsünk egy tisztán szinuszos jelet a következő paraméterekkel:
![]()
Legyen a mintaszám
N=106. Ekkor a kondíciószám: cond(DTD)![]() , melyből jól látszik, hogy a feladat rosszul kondicionált. A kutatás célja a lehető legkisebb kondíciószám elérése és ezáltal a numerikusan stabil kiértékelés biztosítása.
, melyből jól látszik, hogy a feladat rosszul kondicionált. A kutatás célja a lehető legkisebb kondíciószám elérése és ezáltal a numerikusan stabil kiértékelés biztosítása.
Módszerek
A rosszul kondicionáltságot jól láthatóan D mátrix negyedik oszlopa okozza, így a probléma első (és triviális) megközelítése a negyedik oszlop átskálázása [1],[8], [9]. Ez azt jelenti, hogy a negyedik oszlop minden egyes elemét ugyanazzal az értékkel elosztjuk, ezáltal biztosítva, hogy ugyanabba a nagyságrendbe kerüljenek, mint az első három oszlop. (Természetesen ekkor az egyenletrendszer megoldása után kapott negyedik paramétert ugyanezzel a számmal osztani kell, hogy ugyanannak az egyenletrendszernek a megoldásait kapjuk.) Bebizonyítottam [S1], hogy amennyiben a negyedik oszlop elemeit
![]()
skálázási tényezővel osztjuk, úgy néhány közelítés alkalmazásával a kondíciószám általánosan 14,0-ra csökkenthető. A skálázási tényezőt 𝛾-val jelölve az átskálázás után a következő közelítés tehető:
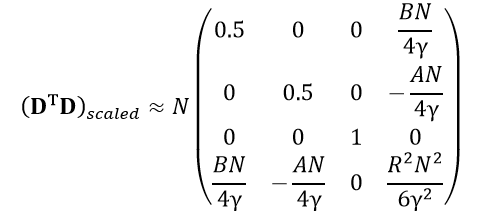
ahol
![]() . A fent említett skálázással jelentős kondiciószám-javulás érhető el, azonban a skálázott
DTD mátrix megfigyelésével jól látható, hogy bár a negyedik sor és oszlop elemei jelentősen csökkenthetők, a mátrix nem válik diagonálissá, mely a numerikus kiértékelés szempontjából kedvező lenne. Adódik tehát a kérdés, hogy a paraméterek megváltoztatásával nem lehet-e kedvezőbb numerikus tulajdonságú problémához jutni.
. A fent említett skálázással jelentős kondiciószám-javulás érhető el, azonban a skálázott
DTD mátrix megfigyelésével jól látható, hogy bár a negyedik sor és oszlop elemei jelentősen csökkenthetők, a mátrix nem válik diagonálissá, mely a numerikus kiértékelés szempontjából kedvező lenne. Adódik tehát a kérdés, hogy a paraméterek megváltoztatásával nem lehet-e kedvezőbb numerikus tulajdonságú problémához jutni.
Ahogy az előző fejezetben láttuk, az egyenletes mintavételezésnél a mintavétel kezdete általában t=0 időpont. Mivel azonban az adatok feldolgozása a teljes mintavételezés lezajlása után történik, ezen időpontnak nincs fizikai jelentése, így szabadon megválasztható. Érdemes tehát ezt a kezdeti t=0 időpontot úgy megválasztani, hogy az a mintavételezett regisztrátum közepére essen, vagyis az időindex -N/2-től N/2-ig fusson (a standard eset helyett, ahol 0-tól N-1-ig fut). Ekkor ugyanis számos szimmetriából adódó előnyt ki lehet használni. A módosítás előtti, és a módosított D mátrix oszlopainak elemei láthatók a következő ábrán:
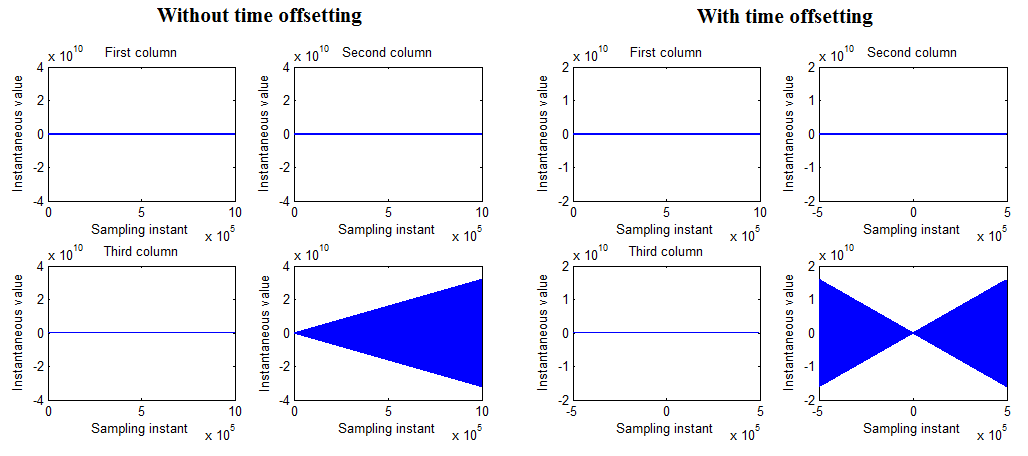
1. ábra: D mátrix oszlopai az időtengely-paraméterek módosítása nélkül és módosításával
Eddigi eredmények
Adódik a kérdés, hogy az időtengely-paraméterek megváltoztatása, vagyis t=0 időpont eltolása mennyiben változtatja meg a probléma numerikus tulajdonságait. Fontos látni, hogy ez a változtatás igen előnyös, ugyanis kihasználja a szinusz páratlan, illetve a koszinusz páros függvény voltát. Amikor a rendszer kondíciószámát meghatározó DTD mátrixot kell kiszámolni, akkor az egyes oszlopok skaláris szorzatát kell meghatározni (vagyis az oszlopok megfelelő elemeit összeszorozni, majd a szorzatokat összeadni). A koszinuszokat és szinuszokat tartalmazó oszlopok skaláris szorzatának számításakor észrevehető, hogy
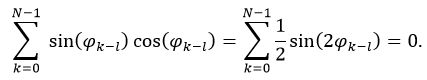
ahol
![]() az időparaméterből kivont ofszet értéke. Az egyenlőség oka, hogy a szinusz páratlan függvény, így az időtengely szimmetriája miatt a vektor első eleme az utolsó elemének ellentettje, a második eleme az utolsó előtti elem ellentettje, és így tovább. Hasonló módon kihasználható, hogy a koszinusz páros függvény, így amikor az egyenkomponenshez tartozó (csupa 1-est tartalmazó oszloppal) összeszorozzuk:
az időparaméterből kivont ofszet értéke. Az egyenlőség oka, hogy a szinusz páratlan függvény, így az időtengely szimmetriája miatt a vektor első eleme az utolsó elemének ellentettje, a második eleme az utolsó előtti elem ellentettje, és így tovább. Hasonló módon kihasználható, hogy a koszinusz páros függvény, így amikor az egyenkomponenshez tartozó (csupa 1-est tartalmazó oszloppal) összeszorozzuk:
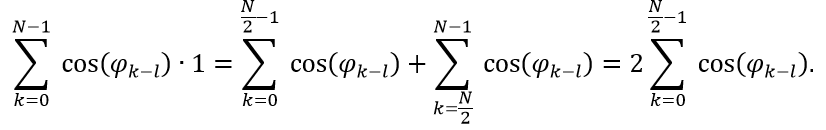
Vagyis a szükséges műveletek száma megfelezhető, ugyanis csak az első N/2 elemet kell kiszámolni (itt feltételeztük, hogy N páros, de páratlan N-re is hasonló összefüggés adható). Hasonlóan kiszámítható DTD többi eleme is. Az eredmény [S1]:
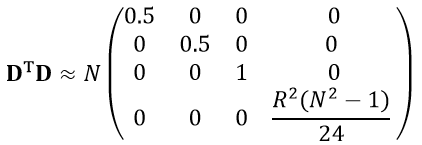
vagyis jól látszik, hogy DTD közel diagonálissá tehető. Ennek következtében, amennyiben
D mátrix harmadik oszlopát osztjuk
![]() -vel, a negyedik oszlopát pedig
-vel, a negyedik oszlopát pedig
![]() -gyel, akkor a következő skálázott mátrixot kapjuk
-gyel, akkor a következő skálázott mátrixot kapjuk

Ezen mátrix kondíciószáma jól láthatóan 1, ugyanis mind a négy szinguláris értéke 0,5. Ezáltal biztosítottuk a numerikus szempontból optimális 1 kondíciószám megközelítését [S1].
Várható impakt, további kutatás
Ahogy a bevezetőben is említésre került, az analóg-digitális átalakítók tesztelése szinuszillesztő algoritmus segítségével történik. Ennek megfelelően az IEEE 1241-es szabvány alapján minden egyes tesztelendő átalakító esetén futtatni kell egy LS szinuszillesztést, így kritikus fontosságú, hogy a teszteket numerikusan stabilan tudjuk végrehajtani [6]. Véleményem szerint kutatásom eredményei bővíthetik az említett szabványt.
A publikációk közül [1], illetve [S1] az IEEE Transactions on Instrumentation and Measurement folyóiratba került benyújtásra, mely az SJR (SCImago Journal & Country Rank) értékelése alapján a Q1 (vagyis felső 25%) besorolású mind ’Electrical and Electronic Engineering’, mind ’Instrumentation’ tudományterületeken.
A kutatás a Dr. Kollár István vezetése alatt folyó “Optimális paraméterbecslési eljárások vizsgálata” OTKA-projekt (azonosító: K-115820) részét képezi. A numerikus javítási lehetőségek fejlesztésként be fognak kerülni a kutatócsoportom által fejlesztett, ingyenesen elérhető MATLAB-toolboxba, melyet már több mint 10 országból töltöttek le [L1].
Saját publikációk
[1] B. Renczes, I. Kollár, A. Moschitta, P. Carbone, „Numerical Optimization Problems of Sine-Wave Fitting Algorithms in the Presence of Roundoff Errors”, Accepted for publication in IEEE Transactions on Instrumentation and Measurement, 2016, doi: 10.1109/TIM.2016.2562218
[2] B. Renczes, I. Kollár, P. Carbone, A. Moschitta, V. Pálfi, T. Virosztek, “Analyzing Numerical Optimization Problems of Finite Resolution Sine Wave Fitting Algorithms”, Proceedings of IEEE International Instrum. Meas. Technology Conference, pp. 1662–1667, Pisa, Olaszország, 2015. május 11–14, doi: 10.1109/I2MTC.2015.7151529
[3] B. Renczes, I. Kollár, ”Roundoff Errors in the Evaluation of the Cost Function in Sine Wave Based ADC Testing”, 20th IMEKO TC 4 Symposium and 18th IWADC Workshop, Benevento, Olaszország, 2014. szeptember 15–17,
URL: http://www.imeko-tc4-2014.org/files/IMEKO_TC4_2014_proceedings.pdf.
[4] B. Renczes, I. Kollár, ”Linearization of A/D converters using interpolation of samples”, 19th IMEKO TC 4 Symposium and 17th IWADC Workshop, Barcelona, Spanyolország, 2013. július 18–19
URL: http://mycite.omikk.bme.hu/doc/144252.pdf
[5] B. Renczes, I. Kollár, “Compensation of Analog-to-Digital Converter Nonlinearities using Dither”, Periodica Polytechnica – Electrical Engineering 57 (3), pp. 77–81, (2013),
doi: 10.3311/PPee.2145
Előkészített publikációk
[S1] B. Renczes, I. Kollár, “Efficient Implementation of Least Squares Sine Fitting Algorithms”, Lényeges felülvizsgálat után benyújtva az IEEE Transactions on Instrumentation and Measurement folyóirathoz
Hivatkozások
[6] Standard IEEE-1241-2010, “IEEE Standard for Terminology and Test Methods for Analog-to-Digital Converters” (2011) doi: 10.1109/IEEESTD.2011.5692956
[7] IEEE Standard-1057-2007, „Standard for Digitizing Waveform Recorders”, 2007
doi: 10.1109/IEEESTD.2008.4494996
[8] P. Ramos, T. Radil, F. Janeiro, “Implementation of sine-fitting algorithms in systems with 32-bit floating point representation”, Measurement 45, pp. 155–163, 2012. doi:10.1016/j.measurement.2011.05.011
[9] K. Chen, Y. Xue, “Improving four-parameter sine wave fitting by normalization”, Computer Standards and Interfaces, vol. 29, pp. 184–190, 2007. doi:10.1016/j.csi.2006.05.005
Linkek
[L1] I. Kollár, T. Virosztek, V. Pálfi, B. Renczes, “ADCTest Project”
http://www.mit.bme.hu/projects/adctest