Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME GPK, Department of Applied Mechanics

Supervisor: Dr. Dombóvári Zoltán

Modeling of machining processes with industrial robots

Introducing the research area.

There is a growing demand in the industry to use robotic arms to machine metal parts, but this application usually requires high geometric accuracy. Robots face two main problems dynamically in these applications. Firstly, unlike dedicated machine tools, a robotic arm has a dynamically weak structure and therefore it is prone to more significant nonlinear behavior [R1] considering e.g., the same amplitude of oscillation. Especially the joints and the drive of the robotic arm can introduce nonlinearities to the stiffness characteristic, which can induce unstable limit cycles even in the case of linearly stable machining, undermining robustness. Secondly, machining processes like turning and milling are regenerative processes [R2] as the past states of the dynamic system play an important role in the long-term behavior of the system. This property, together with the instabilities generated by the delays in feedback loops can have a significant effect on the quality of the process.

Brief introduction of the research place.

The research is carried out at the Department of Applied Mechanics of the Mechanical Engineering Faculty of BUTE. The research is partly conducted in the MTA-BME Lendület Machine Tool Vibration Research Group, which is focused on the improvement of stability and robustness of industrial machine tools.

History and context of the research.

Robots were originally developed for simple pick-and-place [R3] operations, where extreme geometrical accuracy is usually not required. Later, industrial robots were used in some machining applications, especially for clay prototype manufacturing in industrial problems. By that time positioning accuracy was increased by an order with better sensors and built-in proportional derivative control. This precision was sufficient for the aforementioned sculpture-like clay prototype manufacturing, where cutting forces are not significant. This was gradually taken over by 3D printing, but clay in some cases is still a cheap and durable solution to test design issues, e.g., sculpture-like car chassis prototypes for design purposes.

Nowadays, the machining of metal parts with industrial robots shows great promise, mainly because of their versatility and relatively low cost compared to machine tools. Most common open kinematical chain robots are excellent for the manufacturing of sculpture-like surfaces and have a large workspace. The disadvantage is that this versatile configuration lacks rigidity, which is required in the machining of metal parts, and they are prone to strong nonlinear behavior. Furthermore, the vibrational parameters of robots are pose-dependent and can vary on a large-scale during machining, which results in nonautonomous excited dynamical systems.

The research goals, open questions.

The ultimate aim of this research is to prepare stock robots for the demanding task of metal cutting, which at present has many limitations. The correct characterization of the mechanical behavior of robotic arms is as much important as having the mathematical tools to deal with the intricate problems introduced by robotic machining.

The introduced methods provide design options for robotic machining to ensure and improve stability as well as robustness during the operation. The main difficulties arise from the possible strong nonlinear behavior of the stiffness characteristic occurring mainly at the joints and drives, the instabilities arising from the regenerative effect of the machining and delayed feedback controllers, and the time-varying vibrational parameters depending on the path. These problems must be tackled step by step first, allowing a more unified approach at the end. Since these phenomena can and do appear in other problems, we are presenting general mathematical approaches, which can also be used in other engineering applications.

Methods.

Additional acceleration feedback controller to improve performance

The dynamic performance of robots must be upgraded for metal cutting. This could be done by deploying an online control using built-in velocity or acceleration feedback controllers. This would be a relatively simple solution, as no additional cost-increasing equipment would be needed. The problem is, however, that for security reasons the manufacturer usually does not give access to the already installed controllers, so these measured signals cannot be used. Another approach to increase the dynamic reflected stiffness of the end effector is to use mounted passive or semi-active embedded systems. However, industrial robot users are usually not comfortable accepting these solutions. An additional acceleration controller besides the built-in PD controller of the robot can be a relatively cheap and simple solution to improve stability and robustness. To achieve stable manufacturing using the new feedback controller, careful parameter management and the synchronization of time delays of the controllers are necessary. Theoretically, the possible harmful nonlinearities from the robotic configuration can be counteracted using nonlinear state feedback [P1].

 

Effect of quantization in digital controllers

The quantized nature of digital controllers can have a significant impact on the stability of mechanical systems. This is especially true for neutral and advanced systems [R4], where the state depends also on the derivative or the second derivative of past states. The time delay of these digital controllers can be modeled by sawtooth-like time-periodic functions. This time-periodic nature of the controllers together with the possible time periodicity of the machining defines a principal period, which is the necessary time interval for the numerical solution to predict asymptotic stability and usually must be approximated.

 

Time-varying vibrational parameters of robots

The vibrational parameters of robots depend on the posture, which means that during machining these parameters can change on a large scale since they are dependent on the path. The mathematical description results in nonautonomous (generally nonperiodic) dynamical systems having continuously varying coefficients in time. In these systems, it may not be possible to achieve asymptotic stability on the entire time interval, e.g., the whole path of the robot during machining. However, amplitude limits, i.e., finite time stability can be feasible. This requires the accurate prediction of the vibrations, which is not trivial for nonautonomous systems and present state-of-the-art numerical methods cannot provide reliable results. Because of these requirements, the development of an analytical approximate solution is required that will serve as a baseline for future numerical schemes.

Results.

Hopf bifurcation of neutral delay differential equations

A two-degrees-of-freedom nonlinear robot model subject to acceleration feedback control was studied. We consider this as the simplest possible equivalent model that can reproduce the nonlinear behavior with the nonlinear delayed feedback controller, which leads to a neutral system.

Firstly, the linear stability of the mechanical system was studied (Fig. 1(a, b)). The nonlinear properties near the critical bifurcation point were calculated with the center manifold reduction derived for neutral equations [P2]. The analytical approximation was verified with numerical continuation [R5]. The correct choice of nonlinear control parameters ensures stable limit cycles and improves robustness.

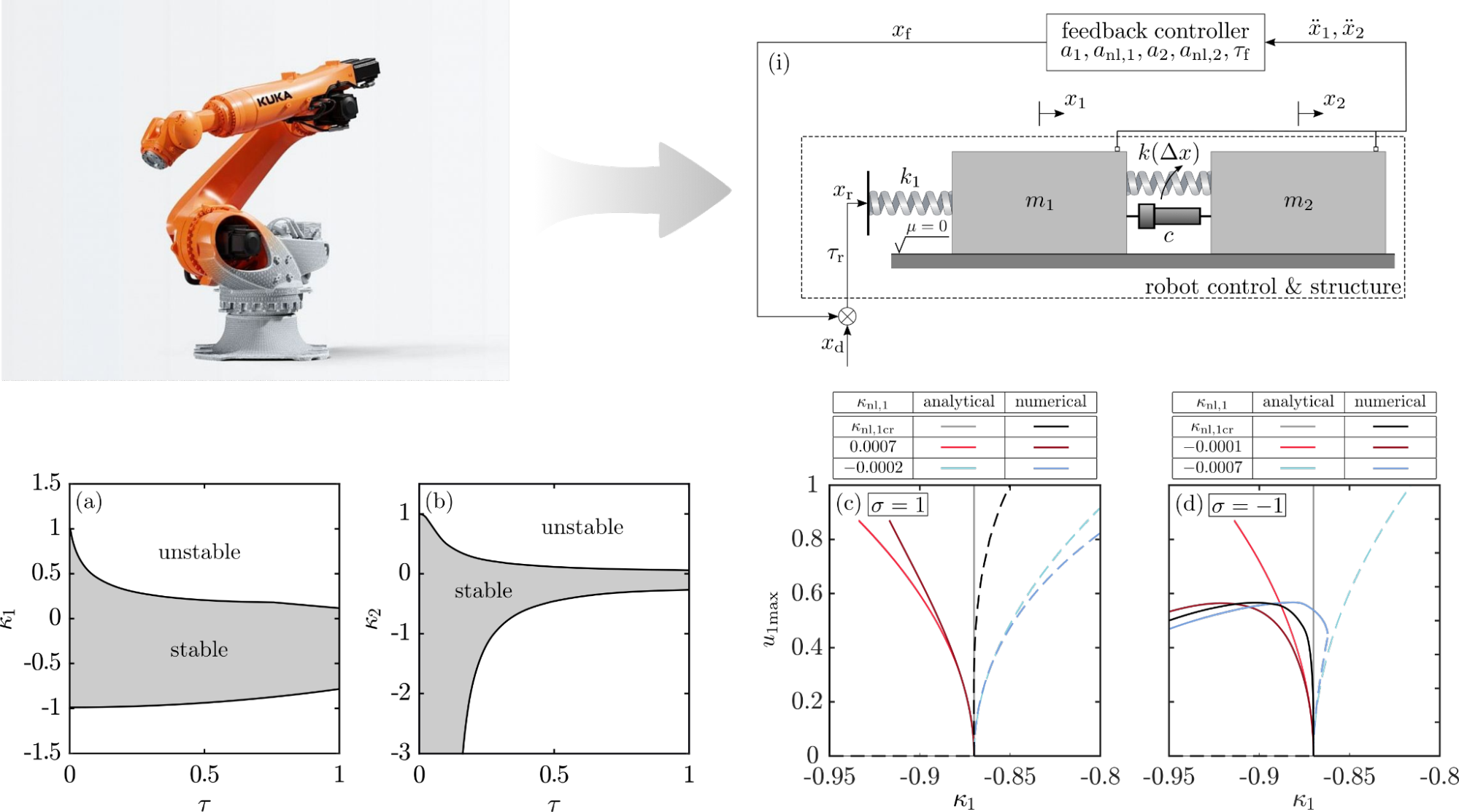
Figure 1: (i) two degrees-of-freedom robot model. (a, b) linear stability analysis. (c, d) analytical and numerical bifurcations for hardening (c) and softening (d) nonlinearities.

 

Stability of robotic machining with digital controllers

The semidiscretization method [R6] was generalized to quantized and continuous delays in a software package that can handle retarded, neutral, and advanced equations. The principal period was approximated by the Farey ratio. This numerical scheme was tested on two engineering applications.

First, the stability analysis of a hierarchical controller of an autonomous vehicle was calculated for which verifying measurements were carried out [P3]. Then, the stability of a robotic arm in milling with built-in PD and additional acceleration controllers resulting in an advanced delay differential equation was studied [C2, P4].

 

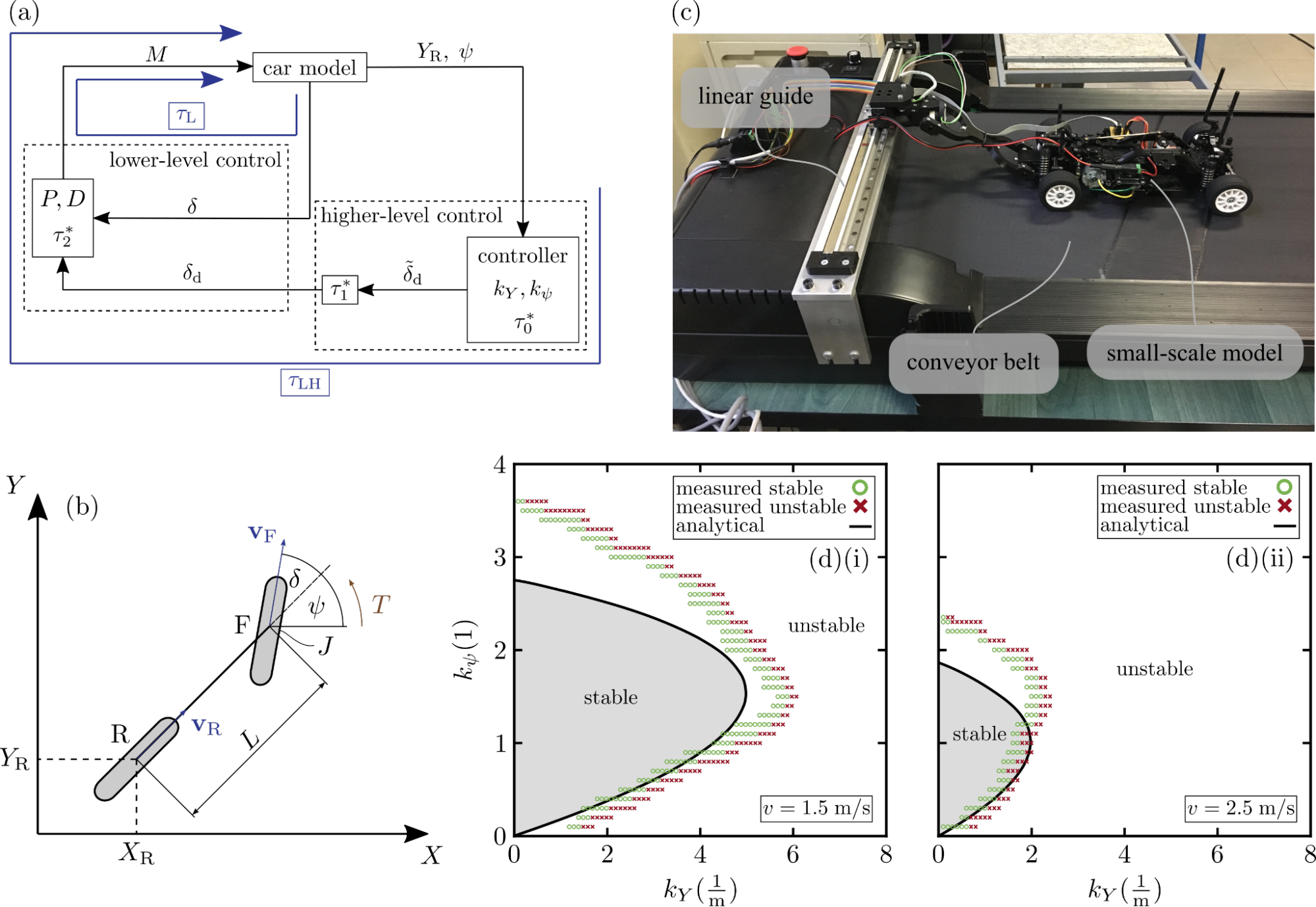
Figure 2: (a) hierarchical steering control. (b) bicycle model of the car. (c) measurement setup. (d) stability with numerical scheme and measurements.

 

 

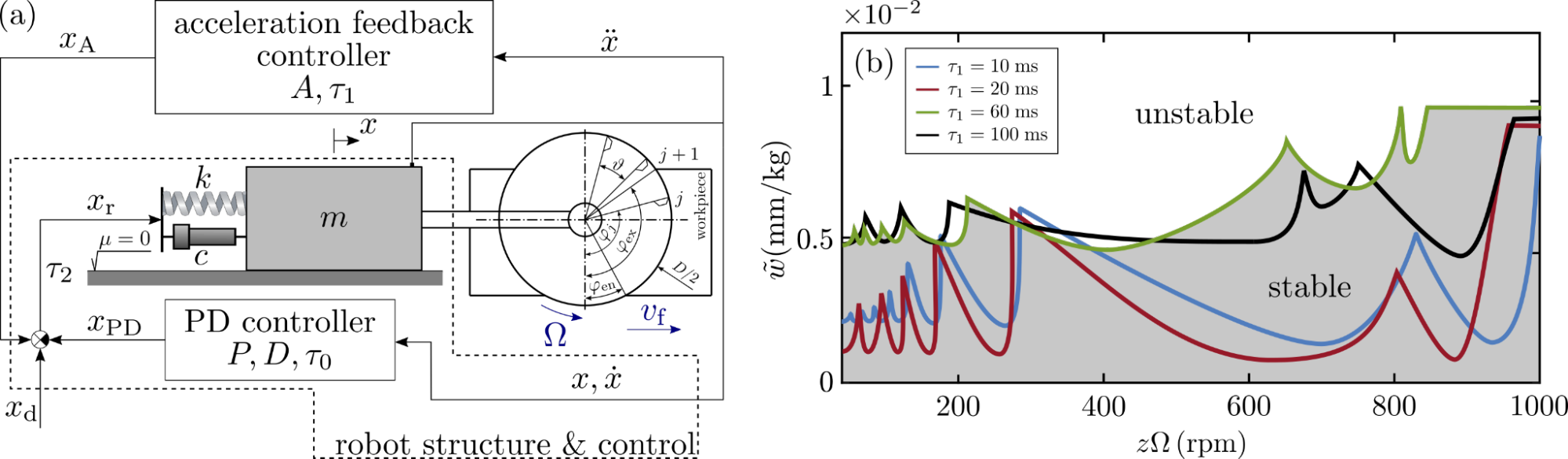
Figure 3: (a) robot structure in milling with additional acceleration feedback controller. (b) stability for different sampling time delays.

 

Analytical approximation of finite time stability of nonautonomous dynamical systems

To correctly approximate the finite time stability of robots, a framework for nonautonomous dynamical systems is needed. We studied the simplest possible case of dynamic stability. For the homogeneous solution, the WKB approximation [R7] can be used if the parameters are slowly varying. For the particular solution, a novel concept was introduced, which is based on the iterative integration-by-parts (IBP) method [C1, P5]. This method is applicable in other engineering cases. The method was verified by an analytical approximation only true for this system. As Fig. 4. shows, available numerical schemes cannot predict finite time stability correctly.

 

Figure 4: (a) eigenvalue functions of dynamic stability loss. (i) analytical and numerical finite time stability. (ii) approximation of particular solution integrals and integral errors. (iii) time domain results.

Expected impact and further research.

If the current problems of robotic machining can be overcome, then several machining tasks can be taken over from machine tools, decreasing cost and time. This can make metal cutting much cheaper and faster which can change the machining industry.

The already achieved results of the research not only serve as important steps in successfully accomplishing robotic machining but they provide general methods that can be used in other engineering problems. The future research goals include the development of a suitable numerical scheme, which can correctly simulate nonlinear problems with time delays and time-varying parameters.

Publications, references, links.

List of corresponding own publications.

Journal papers.

[P1] Habib G., Bártfai A., Barrios A., Dombóvári Z. Bistability and delayed acceleration feedback control analytical study of collocated and non-collocated cases. Nonlinear Dynamics, 108, 2075–2096, 2022. (IF: 5.741)

[P2] Bartfai A., Dombovari Z., Hopf Bifurcation Calculation in Neutral Delay Differential Equations: Nonlinear Robotic Arms Subject to Delayed Acceleration Feedback Control. International Journal of Non-Linear Mechanics, 147, 2022. (IF: 2.985)

[P3] Bartfai A., Vörös I., Takacs D., Stability analysis of a digital hierarchical steering controller of autonomous vehicles with multiple time delays. Journal of Vibration and Control, OnlineFirst, 2023 (IF: 2.633)

[P4] Bartfai A., Barrios A., Dombovari Z., Stability Analysis of a One Degree-of-Freedom Robot Model with Sampled Digital Acceleration Feedback Controller in Turning and Milling. Journal of Computational and Nonlinear Dynamics, 18(8), 2023. (IF: 1.872)

[P5] Bartfai A., Kuske R., Hogan J., Dombovari Z., Framework for the analytical approximation of finite time stability of excited dynamical systems with time-varying parameters. SIAM Journal on Applied Mathematics, 2023. (under submission, IF: 2.148)

 

Conference papers/Book chapters.

[C1] Bartfai A., Kuske, R., Dombovari, Z., On the finite-time stability of dynamic stability loss in a single degree of freedom system. In Proceedings of the ISMA2022 International Conference on Noise and Vibration Engineering, Leuven, 2565–2576, 2022.

[C2] Bartfai A., Barrios, A., Dombovari, Z., Stability Analysis of a One Degree-of-Freedom Robot Model with Sampled Digital Acceleration Feedback Controller in Turning. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (ASME IDETC-CIE2022), St. Louis, 1–8, 2022.

[C3] Bartfai A., Dombovari Z., Demonstration of optimal tuning measurement of the tunable clamping table with a polymer workpiece. 38th Danubia Adria Symposium on Advances in Experimental Mechanics, 2022, no. 3125.

[C4] Bartfai A., Dombovari Z., Bistability in nonlinear elastic robotic arms subject to delayed feedback control. 10th European Nonlinear Dynamics Conference (ENOC 2022), Lyon, 1113–1114, 2022.

[C5] Bartfai A., Barrios A., Dombovari Z., Robotic Machining Applications: Delayed Acceleration Feedback Control in Milling. Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (ASME IDETC-CIE2021), online, 2021, no. 73909.

[C6] Bártfai A., Dombóvári Z., A Case Study on the Stabilization of Advanced Delay Differential Equations with Digital Controllers. 15th IFAC Workshop on Time Delay Systems (TDS2021), online, pp. 234–235, 2021.

[C7] Bártfai A., Vörös I., Takács D., Időkésés és mintavételezés hatása egy autó sávtartó szabályozásában. XXIX. Nemzetközi Gépészeti Konferencia, Cluj, Romania (OGÉT 2021), 204–207, 2021.

[C8] Iklodi Zs., Gabos Z., Bartfai A., Dombovari Z., Time Domain simulation of surface topography in broaching considering tools with general cutting-edge geometries and three DoF parametric dynamics. Manufacturing Engineering Society International Conference (MESIC 2023), Sevilla, Spain, 2023 (accepted paper)

[C9] Bartfai A., Dombovari Z., Demonstration of finite time stability in hardware-in-the-loop turning process with time-varying parameters. 39th Danubia Adria Symposium on Advances in Experimental Mechanics, Siófok, Hungary, 2023 (accepted paper)

[C10] Bartfai A., Dombovari Z., Időben változó paraméterű esztergálás véges idejű stabilitás vizsgálatának numerikus szimuláció problémája. XIV. Magyar Mechanikai Konferencia, Miskolc, Hungary, 2023 (accepted paper)

 

Table of links.

Department of Applied Mechanics

MTA-BME Lendület Machine Tool Vibration Research Group

 

List of references.

[R1] de Luca A., Farina R., Lucibello P., On the control of robots with visco-elastic joints. In: Proceedings. 2005 IEEE International Conference on Robotics and Automation, 4297–4302, 2005

[R2] Munoa J., Beudaert X., Dombovari Z., Altintas Y., Budak E., Brecher C., Stepan G., Chatter suppression techniques in metal cutting. CIRP Annals 65(2), 785–808, 2016.

[R3] Hazarika S.M., Dixit U.S., Robotics: history, trends, and future directions, chap. 7. Materials Forming, Machining and Tribology. Springer International Publishing, 213–239, 2018.

[R4] Insperger T., Stepan G. and Turi J., Delayed feedback of sampled higher derivatives. Philosophical Transactions of the Royal Society A 368(1911): 469–482, 2010.

[R5] Barton D.A. Krauskopf B., Wilson R.E., Collocation schemes for periodic solutions of neutral delay differential equations. Journal of Difference Equations and Applications, 12(11), 1087–1101, 2006.

[R6] Insperger T., Semi-Discretization for Time-Delay Systems. Springer-Verlag New York: Stability and Engineering Applications, 2011.

[R7] Baer S.M., Erneux T., Rinzel J., The slow passage through a Hopf bifurcation: Delay, memory effects, and resonance. SIAM Journal on Applied Mathematics, 49(1), 55–71, 1989.