Matematika- és Számítástudományok Doktori Iskola 

TTK, Sztochasztika Tanszék

Témavezető: Dr. Simon Károly, Konzulens: Dr. Molontay Roland

Lemorzsolódás előrejelzése személyre szabott értelmezhető gépi tanulási módszerek segítségével

A kutatási téma néhány soros bemutatása

A hallgatói lemorzsolódás előrejelzése egy viszonylag új kutatási területhez tartozik, az oktatási adattudományhoz. Az oktatási adattudomány az adattudomány egyik fontos ága, amelynek célja, hogy statisztikai és gépi tanulási módszerek segítségével hasznos információt nyerjen ki a különböző oktatási adatokból. A BME Központi Tanulmányi Hivatalával együttműködve célunk, hogy a Neptunban tárolt adatok feldolgozásával és megértésével segítsük az oktatás szereplőit. Fő kutatási területem a lemorzsolódásban veszélyeztetett hallgatók azonosítása, az egyetemi felvételi pontszám prediktív erejének vizsgálata, valamint a hallgatói sikeresség különböző tényezőinek azonosítása magyarázható mesterséges intelligencia segítségével.

 

A kutatóhely rövid bemutatása

Az oktatási adattudomány a Human and Social Data Science Lab egyik fő kutatási területe. A labor küldetése, hogy az adat- és hálózattudományi alapkutatási eredményeket átültesse üzleti, humán- és társadalomtudományi területekre. Az EduDev Zrt.-vel együttműködve egy KFI projektben azon dolgozunk, hogy a kutatásainkra építve egy publikus MI-alapú alkalmazást fejlesszünk.

 

A kutatás történetének, tágabb kontextusának bemutatása

A hallgatói lemorzsolódás világszerte komoly problémát jelent a felsőoktatásban, különösen a STEM/MTMI (matematikai, természettudományi, mérnöki és informatikai)

képzések esetén, ami jelentős személyes és társadalmi költségeket von maga után. A lemorzsolódásban veszélyeztetett hallgatók gépi tanulási eszközökkel való azonosítása az utóbbi időben nagyobb tudományos érdeklődésre tett szert [1-5]. Bár számos prediktív analitikai kutatás született, ezen tanulmányok túlnyomó többségének pusztán az a célja, hogy minél előbb, minél pontosabban meg tudják különböztetni (osztályozni) a lemorzsolódásban veszélyeztetetteket és a sikeresen diplomázókat. Ezekben a

munkákban azonban a betanított modellek értelmezése és az előrejelzéseik megmagyarázása általában elmarad. Egy jól működő döntéstámogató rendszer azonban amellett, hogy nagy hatékonysággal azonosítani tudja a veszélyeztetett diákokat, képes magyarázatot is adni az előrejelzésre, ezáltal segítve az érintetteket abban, hogy különböző intervenciókkal vagy változtatásokkal növelni tudják a diplomaszerzés esélyét. Ebben a kutatásban a BME adatainak felhasználásával mutatjuk be, hogy az értelmezhető gépi tanulás (IML) és a megmagyarázható mesterséges intelligencia (XAI) eszközei hogyan támogathatják az oktatás résztvevőit a lemorzsolódás előrejelzésében. Az IML és az XAI módszerek segítségével átláthatóvá és értelmezhetővé válnak a komplex „black-box” modellek, ezzel lehetővé téve a személyre szabott útmutatást és felzárkóztatást. Továbbá az előrejelzések magyarázata segít a döntéshozók bizalmának megteremtésében is, ami kulcsfontosságú lépés e megoldások valós oktatási környezetben való telepítésében és alkalmazásában.

 

A kutatás célja, a megválaszolandó kérdések.

Míg a kapcsolódó munkák a hallgatók tanulmányi átlagát és az egyes kurzusokon nyújtott teljesítményt jelzik előre, ebben a kutatásban a célváltozó az egyetemi hallgatók végső tanulmányi teljesítménye, azaz célunk megkülönböztetni a várhatóan diplomát szerző és a lemorzsolódásban veszélyeztetett hallgatókat [MN1]. Ennek a kutatásnak fő céljai a következők:

1. A beiratkozás pillanatában rendelkezésre álló adatok alapján előre jelezni a végső egyetemi teljesítményt (elbocsátott/diplomát szerzett). Azaz, a lemorzsolódásban veszélyeztetett hallgatók azonosítása gépi tanulási eszközök segítségével.
2. A gépi tanulási modell értelmezése globálisan és lokálisan. Először azonosítjuk a legfontosabb tényezőket, és megvizsgáljuk az előrejelzésre gyakorolt hatásukat. Ezután – a kapcsolódó munkák többségével [6-7] ellentétben – lokális magyarázatot adunk az előrejelzésekre, azaz tanulmányozzuk az egyéni előrejelzések mögött meghúzódó okokat: miért veszélyeztetett egy hallgató?

 

Módszerek

Ez a tanulmány a Budapesti Műszaki és Gazdaságtudományi Egyetem (BME) adatain alapul, ami 8 508 olyan hallgató adatait tartalmazza, akik 2013 és 2017 között iratkoztak be (valamelyik alapképzésre), és azóta valamilyen úton befejezték tanulmányaikat: vagy diplomát szereztek, vagy lemorzsolódtak. Adathalmazunk változói többnyire a beiratkozás előtti tanulmányi teljesítménymutatók, amelyek a felvételi pontszám komponensei, tehát amiken az egyetemi felvételi eljárás alapul [MN2]. Pontosabban, a változók többsége a középiskolai osztályzatokra és az érettségin elért eredményekre vonatkozik. A középiskolai teljesítményt a középiskolai tanulmányi átlaggal (KTÁtlag) mérjük. Az érettségivel kapcsolatos változók pedig különböző tantárgyakból (például történelemből és matematikából) elért eredményekből állnak.

Az egyetemi teljesítmény előrejelzésére a CatBoost algoritmust használjuk, ami számos tabuláris benchmark adathalmazon a legjobb modellnek bizonyult [8], valamint ilyen adathalmazokon a modern mélytanulási modellek is rendszerint alulteljesítenek a CatBoost-hoz hasonló modellekhez képest [9-10].

A modell értelmezéséhez olyan modern módszereket alkalmazunk, mint a kétdimenziós parciális függőségi diagram [11] és a SHAP-értékek [12], amelyek a játékelméleti Shapley-érték koncepcióján alapulnak.

A parciális függőségi diagramokat (PDP) a globális értelmezéshez használjuk. A PDP, vagy másképp interakciós diagram azt mutatja, hogy két jellemző milyen marginális (parciális) hatással van a modell előrejelzésére [11].

A lokális értelmezéshez, azaz az egyéni előrejelzések alaposabb megértéséhez a SHAP-értékeket használjuk, amelyek az egyes változók adott előrejelzéshez való hozzájárulását adják meg. Pontosabban, a változók hozzájárulását a modell átlagos kimenetéhez (predikciójához) hasonlítjuk, amelyet alapértéknek nevezünk. A SHAP-érték tehát egy lokális előrejelzést úgy magyaráz meg, hogy megmutatja, hogyan és milyen mértékben mozdítják el a hallgató változóinak értékei a modell előrejelzését az alapértékhez viszonyítva [12]. Megjegyzendő, hogy a SHAP-értékek aggregálásával a változók globális fontosságát is megkaphatjuk.

 

Eddigi eredmények

Számos gépi tanulási modellt teszteltünk, és azt találtuk, hogy a CatBoost teljesített a legjobban, 0,847-es átlagos pontossággal és 0,774-es AUC-értékkel. Eredményeink összhangban vannak a kapcsolódó tanulmányokkal, amelyek hasonlóan nagy heterogén adathalmazon végeznek lemorzsolódás-előrejelzést (pl. Behr és munkatársai [13] 0,77-es AUC-ot, Lee és Chung [14] pedig 0,898-as átlagos pontosságot értek el). Modellünk tehát pontosan azonosítja a veszélyeztetett tanulókat, így érdemes és indokolt a modell értelmezése az XAI eszközeivel.

 

1.

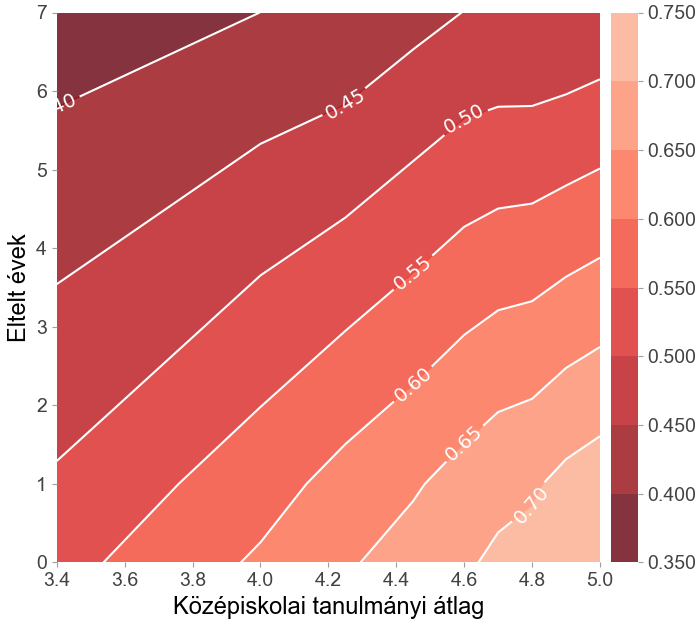
ábra. A matematika és a történelem interakciós kétdimenziós parciális függőségi diagramja és a középiskolai tanulmányi átlag interakciója “Eltelt évekkel” (az érettségi és az egyetem között eltelt évek száma).

 

A változók előrejelzésre gyakorolt együttes hatásának megértéséhez a kétdimenziós parciális függőségi ábrákhoz fordulunk. Az 1. ábra bal oldali diagramja a matematika és történelem érettségi pontszámok különböző kombinációihoz tartozó előrejelzéseket mutatja. Az ábra azt sugallja, hogy minél jobb a matematika érettségi eredmény, annál nagyobb a CatBoost modell kimenete, azaz a végzés jósolt valószínűsége. Továbbá a legmagasabb végzési valószínűség akkor érhető el, ha a történelem érettségin elért pontszám is viszonylag magas. Azonban, ha valaki kiemelkedő eredményt ér el emelt szintű matematika érettségin, és a történelem érettségin elért pontszáma „túl” magas, akkor a diplomaszerzés előre jelzett valószínűsége kissé csökken. A jobb oldali ábra arra utal, hogy ha a végzős középiskolások nem kezdik meg egyetemi tanulmányaikat közvetlenül az érettségi után, akkor a kihagyott évek számának növelésével egyre csökken a diplomaszerzés esélye. Emellett természetesen a hallgatók nagyobb eséllyel szereznek diplomát, ha a középiskolában kiváló osztályzatokat szereznek.

 

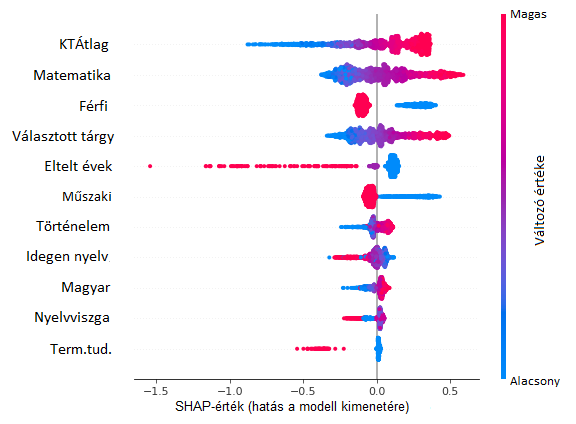
2. ábra A változók hatását összegző grafikon. Minden hallgatónak megfelel egy-egy pont minden sorban. A pontok színe a változó értékét jelöli, az x-tengely pedig a modell előrejelzésére gyakorolt hatást mutatja. A jellemzők a fontosságuk (a modell kimenetére gyakorolt átlagos abszolút hatás) szerint vannak rendezve.

 

A 2. ábra a változók hatását szemlélteti a modell predikciójára vonatkozóan a SHAP-értékek szerint. Az ábra azt mutatja, hogy a legfontosabb változó a középiskolai tanulmányi átlag, és minél magasabb a tanulmányi átlag, annál nagyobb a diplomaszerzés esélye. Mivel a vizsgált egyetem egy műszaki egyetem, nem annyira meglepő, hogy a matematikai készség nagymértékben képes előre jelezni a végső tanulmányi sikert. Hasonló összefüggés van a választott tantárgy és diplomaszerzés valószínűsége között is. Ez valószínűleg annak köszönhető, hogy a felvételi rendszerben a választott érettségi tárgynak a legtöbb esetben kapcsolódnia kell a szakterülethez. Megfigyelhetjük, hogy a 2. ábra szerint az a tény, hogy valaki férfi, negatív hatással van a modell kimenetére. Ez összhangban van korábbi munkánkkal [NM2], ahol kimutattuk, hogy a nők nagyobb valószínűséggel szereznek diplomát a BME-n, mint a férfiak.

 

 

 

 

 

3. ábra Három diák egyéni előrejelzéseinek magyarázata a SHAP-értékek segítségével. Az alapérték (végzés átlagos valószínűsége a modell szerint) 0,67. A modell predikcióját az alapértéktől magasabbra toló faktorok piros színnel, az előrejelzést alacsonyabbra húzó tényezők pedig kékkel vannak jelölve. A sávok hossza megfelel a változók hozzájárulásának mértékének

 

A 3. ábra három hallgató példáján mutatja be az egyéni előrejelzések magyarázatát SHAP-értékek segítségével. Az első tanuló esetében a diplomaszerzés becsült valószínűsége 0,27, ami azt jelenti, hogy ennek a hallgatónak az esetében magas a lemorzsolódás kockázata, továbbá a SHAP-értékek azt is elárulják, hogy miért. Semmi sem tolja feljebb az előrejelzést, de az a tény, hogy a középiskola és az egyetem között 4 év telt el, valamint, hogy a matematika pontszám és a középiskolai átlag viszonylag alacsony, jelentősen csökkenti a modell előrejelzését. A második példa egy közepes diákot mutat, akinek például az érettségi pontszáma a választott tantárgyból magas, de a gyengébb matematikai eredmény lefelé tolja a predikciót, és ezzel ,,kioltja’’ az előbbi pozitív hatást. Az utolsó példa egy tehetséges diákot mutat be, akinek kiváló tanulmányi átlaga és érettségi eredményei vannak, ráadásul a tény, hogy a nők nagyobb valószínűséggel szereznek diplomát a BME-n, még magasabbra tolja a végzés valószínűségét.

 

 

Várható impakt, további kutatás

Eljárásunk újdonsága, hogy nemcsak a végzés valószínűségét becsüljük meg, hanem interpretálhatóvá tesszük a modellt, és az egyéni előrejelzéseket is megmagyarázzuk, ami döntéstámogató eszközként szolgálhat minden érdekelt fél számára. Például segíthet a középiskolásoknak a megfelelő szak kiválasztásában, és pályaorientációs tanácsadást nyújthat azáltal, hogy a középiskolai teljesítménymutatók alapján megbecsüli, hogy melyik szakon lehetnek a legsikeresebbek. Ezenkívül a predikciók lokális magyarázata abban is segítheti a diákokat, hogy azonosítsák azokat a készségeket, amelyeket fejleszteni kell, hogy sikeresek legyenek az egyetemi tanulmányaikban. Továbbá a bemutatott módszertan a felsőoktatási döntéshozók számára is hasznos lehet, hogy megtalálják a megfelelő beavatkozási pontokat a veszélyeztetett diákok számára, például személyre szabott korrepetálás vagy felzárkóztató kurzusok ajánlásával.

A kutatás eredményeit hamarosan egy nyilvánosan elérhető alkalmazásba fogjuk beépíteni, amit az EduDev Zrt-vel közösen fejlesztünk.

 

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

[MN1] Nagy, M., & Molontay, R. (2023). Interpretable Dropout Prediction: Towards XAI-Based Personalized Intervention. International Journal of Artificial Intelligence in Education, 1–27.

[MN2] Nagy, M., & Molontay, R. (2021). Comprehensive analysis of the predictive validity of the university entrance score in Hungary. Assessment & Evaluation in Higher Education (pp. 1–19)

[NM3] Baranyi, M., Nagy, M., & Molontay, R. (2020). Interpretable deep learning for university dropout prediction. Proceedings of the 21st Annual Conference on Information Technology Education (pp. 13–19)

[NM4] Molontay, R., & Nagy, M. (2022). How to improve the predictive validity of a composite admission score? a case study from Hungary. Assessment & Evaluation in Higher Education (pp. 1–19)

[NM5] Nagy, M., Molontay, R., & Szabó, M. (2019). A web application for predicting academic performance and identifying the contributing factors. 47th Annual Conference of SEFI (pp. 1794–1806)

[NM6] Nagy, M., & Molontay, R. (2018). Predicting dropout in higher education based on secondary school performance. In 2018 IEEE 22nd international conference on intelligent engineering systems (INES) (pp. 389–394). IEEE.

[NM7] Kiss, B., Nagy, M., Molontay, R., & Csabay, B. (2019). Predicting dropout using high school and first-semester academic achievement measures. In 2019 17th international conference on Emerging eLearning Technologies and Applications (ICETA) (pp. 383–389). IEEE.

[NM8] Nagy, M. (2023). Lemorzsolódás előrejelzése személyre szabott értelmezhető gépi tanulási módszerek segítségével. Scientia et Securitas, 3(3), 270–281.

 

Linkgyűjtemény.

Saját publikációk (MTMT)

Google Scholar profil

BME Human and Social Data Science Lab

 

Hivatkozások listája.

[1] Alyahyan, E., & Düştegör, D. (2020). Predicting academic success in higher education: literature review and best practices. International Journal of Educational Technology in Higher Education, 17(1), 1–21.

[2] Helal, S., Li, J., Liu, L., Ebrahimie, E., Dawson, S., & Murray, D. J. (2019). Identifying key factors of student academic performance by subgroup discovery. Int J Data Sci Anal, 7(3), 227–245.

[3] Márquez-Vera, C., Cano, A., Romero, C., Noaman, A. Y. M., Mousa Fardoun, H., & Ventura, S. (2016). Early dropout prediction using data mining: a case study with high school students. Expert Systems, 33(1), 107–124.

[4] Rovira, S., Puertas, E., & Igual, L. (2017). Data-driven system to predict academic grades and dropout. PLoS One, 12(2), e0171207.

[5] Varga, E. B., & Sátán, Á. (2021). Detecting at-risk students on computer science bachelor programs based on pre-enrollment characteristics. Hungarian Educational Research Journal, 3(11), 297–310.

[6] Mingyu, Z., Sutong, W., Yanzhang, W., & Dujuan, W. (2021). An interpretable prediction method for university student academic crisis warning. Complex & Intelligent Systems, 8, 1–14.

[7] Karlos, S., Kostopoulos, G., & Kotsiantis, S. (2020). Predicting and interpreting students’ grades in distance higher education through a semi-regression method. Applied Sciences, 10(23), 8413.

[8] Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A. V., & Gulin, A. (2018). Catboost: unbiased boosting with categorical features. Proceedings of the 32nd International Conference on Neural Information Processing Systems (NeurIPS’18) (pp. 1–11)

[9] Grinsztajn, L., Oyallon, E., & Varoquaux, G. (2022). Why do tree-based models still outperform deep learning on typical tabular data? In: Thirty-sixth Conference on Neural Information Processing Systems Datasets and Benchmarks Track.

[10] Shwartz-Ziv, R., & Armon, A. (2022). Tabular data: Deep learning is not all you need. Inform Fusion, 81, 84–90.

[11] Greenwell, B. M., Boehmke, B. C., McCarthy, A. J. (2018). A simple and effective model-based variable importance measure. arXiv preprint arXiv:180504755.

[12] Lundberg, S. M., & Lee, S. I. (2017). A unified approach to interpreting model predictions. In I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, & R. Garnett (Eds.), Advances in Neural Information Processing Systems 30 (pp. 4765–4774).

[13] Behr, A., Giese, M., Theune, K., et al. (2020). Early prediction of university dropouts – a random forest approach. Jahrbücher Für Nationalökonomie Und Statistik, 240(6), 743–789.

[14] Lee, S., & Chung, J. Y. (2019). The machine learning-based dropout early warning system for improving the performance of dropout prediction. Applied Sciences, 9(15), 3093.