
|
BMe Research Grant |

|
Géza Pattantyús-Ábrahám PhD School in Mechanical Engineering
Department of Applied Mechanics
Supervisior: Dr. Gábor Stépán
Stability of the milling process and the quality of the machined surface

Introducing the research area
The scope of the research is modeling of milling processes from the viewpoint of harmful vibrations with special attention to the stability of stationary milling in the case of given machining parameters and machine tool dynamics. This allows the prediction of the machined surface geometry and its quality.

Brief introduction of the research place
In the HAS-BUTE Research Group on Dynamics of Machines and Vehicles, five full time and four part time researchers work on dynamical problems of contacts like elastic wheel rolling on rigid ground, force control of robots contacting rigid environments or humans and cutting processes like turning, milling and drilling subject to regenerative vibration effects.
History and context of the research
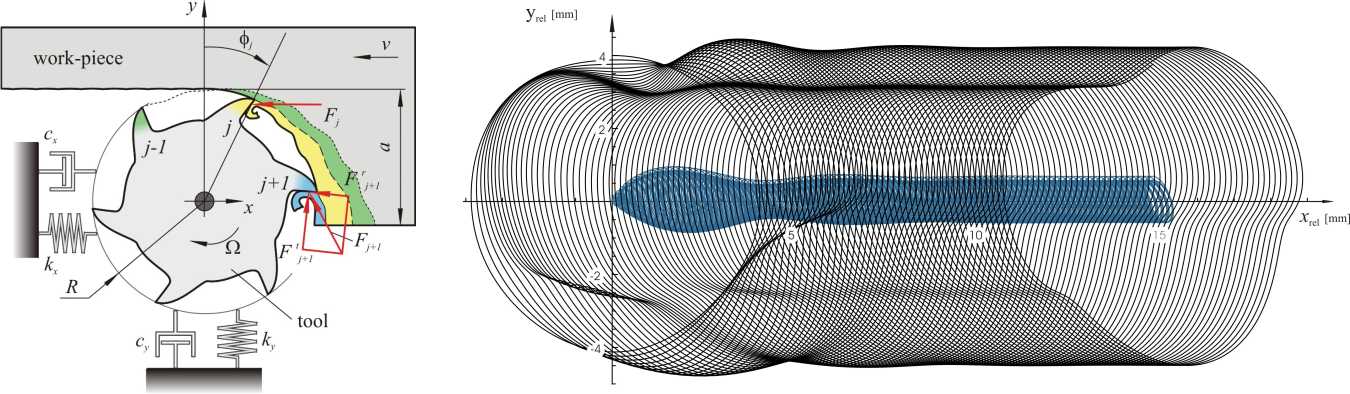
Machine tool vibrations are among the most critical problems in the practice of manufacturing technology. Undesired vibrations arising during machining shorten the lifetime of tools and result in unacceptable surface quality. The two main sources of these vibrations are as follows,
The first one is caused by the periodically varying cutting force. Amplitude of the corresponding forced vibration may become very large if one frequency component of the periodic cutting force is close to any of the natural frequencies of the system. This is the phenomenon of resonance.
The second possible source of vibration is the regenerative effect originated in the wavy machined surface. The chip thickness depends on the current position of the cutting edge and the past position of the previous/neighbouring cutting edge of the mill. This phenomenon can be described by delayed differential equations. Self-excited vibration, the so––called "chatter" occurs if the stationary milling process corresponding to the above described periodic forced vibration becomes unstable. These vibrations result in poor surface quality.
In milling processes, only stable machining is allowed. To avoid self-excited vibrations, the so-called stability chart can be constructed as a function of the machining parameters. There are some regions of these parameters where large material removal rates can be achieved without the occurrence of regenerative chatter. In most cases, however, forced vibrations can still occur with these parameters even close to resonance. These vibrations lead to manageable surface errors.
Aim of the research
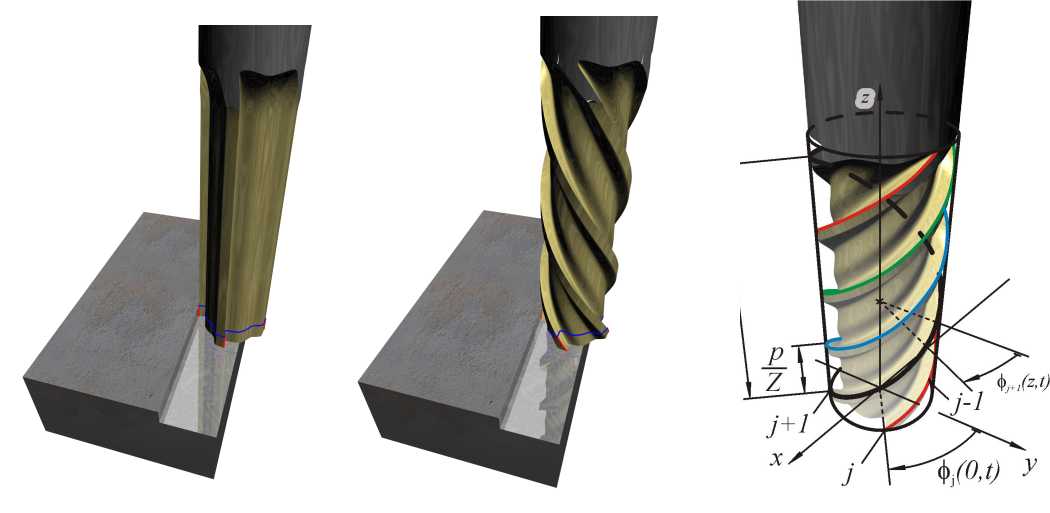
The standard models used in the specialist literature describe the milling tool as a straight fluted one, even though most of them have helical edges. One of our goals is to create an advanced analytical description of milling with helical tools that also describe and characterize the machined surface in three dimensional space.
Based on our results, it is shown that the amplitude of the forced vibrations can be in the range of the tool diameter in the case of near-resonant excitation for certain technological parameters. Existing models usually neglect the amplitude of this type of vibration; therefore, forced- and self-excited vibrations can be treated separately due to the constant time-delay in the governing equations. Our goal is to analyse these two kinds of vibrations together and to show the effects of large amplitude near-resonant vibrations on the stability chart.
Our calculations have proved that the above described coupling effect is stronger if the velocity amplitude of the vibration is in the range of the cutting speed. In the slow spindle speed range, this can occur at small vibration amplitudes, however, in these further effects – such as the so-called "process-damping" which indicates that the stability boundaries are shifted in the direction of larger axial immersion – become significant as well. To study this process damping, we introduced new and more precise distributed delay models.

Methods
When describing the helical fluted milling tool, we also considered the spatial shape of the cutting edge, i.e. the fact that the edge of the tool entered the material at different vibration phases according to their axial coordinate. Consequently, the Surface Location Error, which is commonly used in planar models, varies along the axial coordinate. The resultant cutting force can be computed analytically from an integral with time varying limits, and the corresponding periodic forced vibration is computed by means of Fourier series. The representative spatial surface segment is determined and its geometrical properties are described by three parameters: maximal surface location error, surface roughness in feed- and axial directions. The stability of forced motion is computed by the semi-discretization method, which is based on the Floquet theory extended for delay differential equations.
In the case of large amplitude near-resonant vibrations, a more detailed model is necessary to describe the chip thickness. The accurate mechanical model resulted in a time delay that is a function of the previous path of the neighbouring tooltip, that is, a function of the current and the previous tool positions. The governing equation is formed by a state-dependent delay differential equation, which is essentially a non-linear equation, so the forced and the self-excited vibrations cannot be separated. Due to the non-linearity, periodic solutions can only be calculated using our continuation method. The linearization of the state-dependent delay model is also difficult and can lead to singular equations for certain conditions. The stability of the linearized equation can then be analyzed using the above described semi-discretization method.
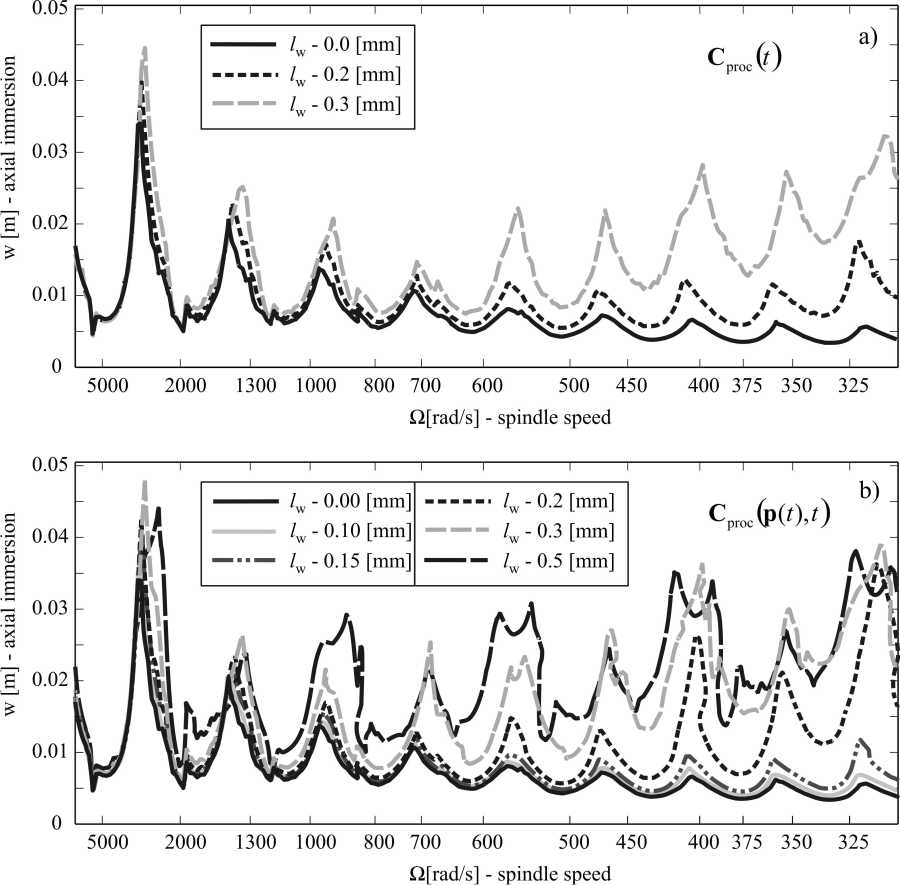
In the low spindle speed domain, process-damping effect has also to be taken into account. There are numerous mathematical models available to explain the increase of stability limits. One of the earliest contains a viscous damping term that is linearly proportional to the time delay, that is, inversely proportional to the spindle speed. It is known from theory that process damping is derived from the contact force created by the elastically deformed workpiece material under the worn flank face. The latest model covers the short-regenerative effect, where the cutting force is described with the chip-flow on the rake face and which leads to a governing equation with distributed time-delay terms. Due to its complicated mathematics, this model is mainly used for turning. In our study, it is shown that the above described process damping is the first approximation of a short-delay model. The damping term which we introduced in our model is a piecewise-constant function of the tooltip velocity and leads to non-linear governing equations, which can be analyzed by using the mentioned methods.
Results
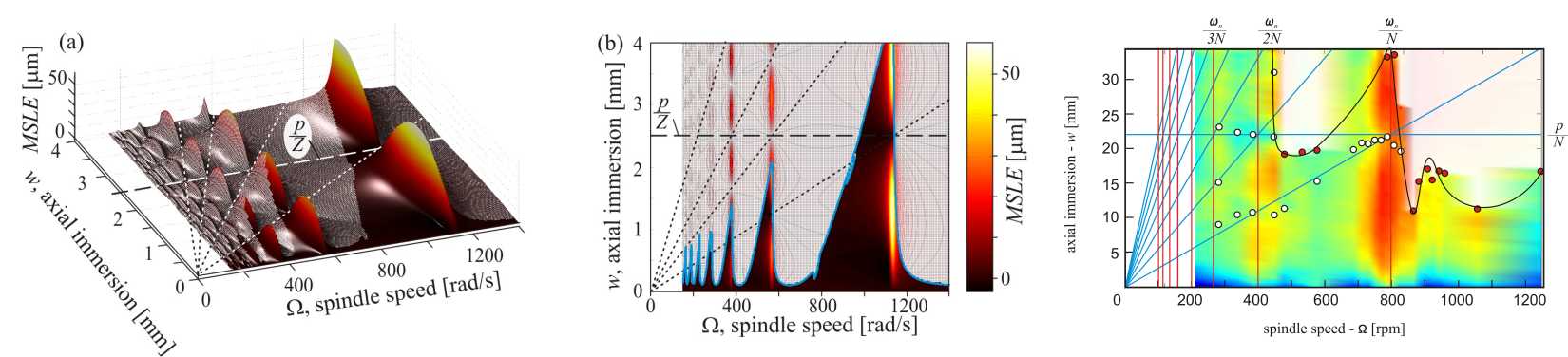
The workpiece surface for the parameter region of stable cutting was generated in the case of helical fluted tool. New surface parameters were introduced to characterize the properties of the surface. The most important observation is that good surface properties and small vibration level can be achieved even for resonant cutting velocities if appropriate axial immersion values are applied. Some of these values are the trivial ones, where the cutting force is constant, i.e., where the axial immersions are equal to an integer multiple of the helix pitch over the number of cutting teeth. Non-trivial appropriate axial immersions depending linearly on the spindle speed have also found been found. At critical resonant cutting speeds, these are equally spaced between the trivial appropriate axial immersions. Our analytical results were validated by measurements on an industrial milling machine.
In our improved milling model of the large amplitude vibrations, a detailed analysis of the stability chart proved that for near-resonant angular velocities; the traditional model of small oscillations can overestimate the extension of stable region. Based on the bifurcation diagram of the forced periodic solution, we have also found an unusual fold bifurcation, which creates a bistable region, where the stationary milling process is not globally stable. The size of this bistable zone was estimated considering the limitation of our model.
When investigating the low spindle speed domain, an improved process damping model was constructed for milling processes. The contact force at the flank face is generated by the compressed workpiece material under the worn flank face. This force can be characterized by a velocity dependent time-periodic damping matrix. It was It was shown that the above described process damping model was the first approximation of a short-delay model. This means that the introduced process damping model can still be inaccurate in the "very" slow speed range, where the wavelength of the oscillation is in the range of the flank wear size. Stability charts were computed for different sizes of flank wear and it was shown that the pattern of the stability lobes were changing for increasing size of the flank wear. This effect is related to the introduced time-periodic velocity-dependent process damping coefficients.

Expected impact and further research
Identification of the non-trivial appropriate axial immersions of helical milling tools is of great practical importance because these are exactly the resonant cutting speeds that allow high material removal rates under stable (chatter-free) machining conditions.
The results of the state-dependent time delay equation of the milling model call the attention to possible uncharted instabilities and new kind of vibrations in those parameter regions where large axial depth of cut can be applied between two instability lobes. Parameters in the bistable zone may lead to new surface patterns and unexpected perturbation-driven switches between them.
In the study of the milling model with process damping effect, it was proved that the above described process damping model was the first approximation of a short-delay model. It was shown that the pattern of the stability lobes varied for increasing size of the flank wear. This effect is related to the introduced time-periodic velocity-dependent process damping coefficients.
Further research aims at combining the above described models to make it applicable in a wide range of machining parameters. We also try to perform further measurements to validate the above described models.
Publications, references, links
Reviewed journal papers
Bachrathy D, Stepan G, Turi J: State dependent regenerative effect in milling processes, Computational and Nonlinear Dynamics (2010), submitted.
Bachrathy D, Insperger T, Stepan G: Surface properties of the machined workpiece for helical mills, Machining Science and Technology 13 (2009) pp. 227–245. DOI 10.1080/10910340903012167.
Bachrathy D, Mészáros I: Dynamical Investigation of high precision hard turning in case of interrupted surfaces, Gépgyártás XLIX:(4–5) (2009) pp. 47–53. (in Hungarian)
Conferences
Bachrathy D, Mészáros I: Optimal cutting speeds, entrance and exit force in interrupted high precision hard turning, 7th International CIRP Conference on Intelligent Computation in Manufacturing Engineering (ICME). (Capri, Italy, 2010) pp. 1–4.
Bachrathy D, Stepan G: Time-periodic velocity-dependent process damping in milling processes, 2nd International CIRP Process Machine Interaction (PMI) Conference. (Vancouver, Canada, 2010) pp. 1–12. ISBN: 978-0-9866331-0-2
Bachrathy D, Reith M J, Mészáros I: Optimal cutting speeds and surface prediction in interrupted high precision hard turning, 7th International Conference on Mechanical Engineering. (Budapest, Hungary, 2010) pp. 241–246. ISBN: 978-963-313-007-0
Bachrathy D, Mészáros I: Dynamical problems in interrupted high precision hard turning, LAMDAMAP 2009: 9th International Conference and Exhibition on Laser metrology, machine tool, CMM and robotic performance. (London, Anglia, 2009) pp. 357–367. ISBN:978-0-9553082-7-7
Bachrathy D, Stépán G: Bistable parameter region caused by velocity dependent, 12th CIRP Conference on Modelling of Machining Operations. (San Sebastian, Spain, 2009) pp. 867–871. ISBN:978-84-608-0866-4
Mészáros I, Bachrathy D, Farkas B: Dynamical problems in high precision hard cutting, Manufacturing 2008: Biannual 19th International Conference on Manufacturing. (Budapest, Hungary, 2008) pp. 18–24. ISBN:978-963-9058-24-8
Bachrathy D, Stépán G: Experimental Setup for Fast Stability Chart Reconstruction of Milling Processes,
6th International Conference on Mechanical Engineering. (Budapest, Hungary, 2008) pp. 1–7. ISBN:978-963-420-947-8
Bachrathy D, Stepan G: Efficient experimental detection of milling stability boundary and the optimal axial immersion for helical mills, in Proceedings of the International Multi-Conference on Engineering and Technological Innovation, (Orlando, Florida, 2008) Vol I, pp. 7–11. ISBN: (13) 978-1-934272-43-5
Bachrathy D, Homer M, Insperger T, Stepan G: Surface location error for helical mills, 6th International Conference on High Speed Machining (San Sebastian, Spain, 2007) (CD-ROM) pp. 379–384.
Bachrathy D, Stepan G: Good surface properties at efficient technological parameters in milling process, 24th Danubia-Adria Symposium (Sibiu, Romania, 2007) pp. 45–46. ISBN:978-973-739-456-9
Bachrathy D, Insperger T, Stépán G: Computation of surface quality in case of helical milling tools. X. Magyar Mechanikai Konferencia. (Miskolc, Hungary, 2007) pp. 1–4. (in Hungarian)
Bachrathy D, Stepan G: Surface error for helical mills, 6th International Congress on Industrial and Applied Mathematics (Zurich, Switzerland, 2007) (CD-ROM: IC/MT(MP669)1083/151) pp. 1–6.
Links
HAS-BUTE Research Group on Dynamics of Machines and Vehicles
Department of Applied Mechanics
My Youtube videos:
Experimental validation of the
"appropriate axial immersions"
Representation of the milling
process created by a helical futed tool
Representation of the period
doubling motion of the milling
tool
