Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola

Műszaki Mechanikai Tanszék 

Témavezető: Dr. Stépán Gábor

A marási folyamat stabilitása és a megmunkált felület minősége

A kutatási téma bemutatása

A kutatás témája a kialakult rezgések figyelembevétele a marási folyamat mechanikai modellezésekor, különös tekintettel a stacionárius forgácsolás stabilitásának pontos meghatározására adott technológiai és szerszámgép-dinamikai paraméterek mellett. Ezek alapján tervezhető a forgácsolás során létrehozott felület geometriája és a megmunkált felület minősége.

A kutatóhely rövid bemutatása

Az MTA-BME Gépek és Járművek Dinamikája Kutatócsoportban öt teljes állású és négy részállású kutató dolgozik különböző dinamikus érintkezési feladatokon, mint amilyen a rugalmas kerekek gördülése merev útfelületen, merev környezettel vagy emberekkel érintkező robotok erőszabályozása és a forgácsolási folyamatok, többek között az esztergálás, marás és fúrás regeneratív rezgései.

A kutatás történetének, tágabb kontextusának bemutatása

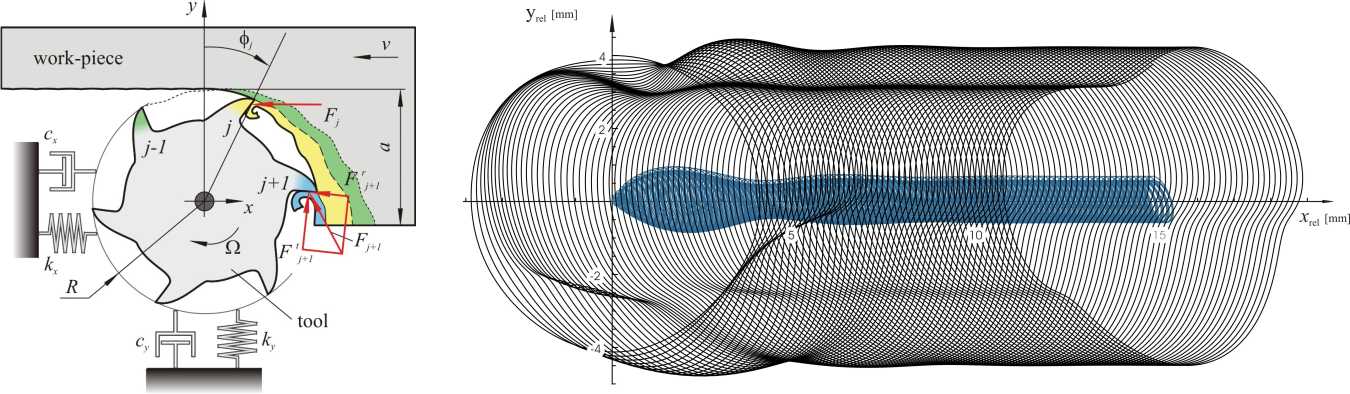
A gyártástechnológiai gyakorlat egyik legkritikusabb problémáját a szerszámgéprezgések jelentik. A megmunkálás során keletkező nemkívánatos rezgések csökkenthetik a szerszám élettartamát és tönkretehetik a megmunkált felületet. A rezgéseknek az alábbi két fő forrása van.

Az egyik ok a periodikusan változó forgácsoló erő, amely hatására kialakuló erő-gerjesztett rezgés amplitúdója igen nagy lehet, ha a forgácsolóerő egyik felharmonikusának frekvenciája a rendszer egyik sajátfrekvenciájának közelébe esik. Ezt a jelenséget hívjuk rezonanciának.

A másik lehetséges ok a regeneratív hatás, amely a megmunkált felület hullámosságából ered. A kialakult forgácsvastagság függ a marószerszámél pillanatnyi és a megelőző forgácsolóél múltbeli pozíciójától. Ezt a jelenséget időkésleltetett differenciálegyenletekkel lehet leírni. Öngerjesztett rezgés, az úgynevezett „chatter” akkor alakul ki, ha a stacionárius forgácsolási folyamat, azaz az előbb említett erő-gerjesztett rezgés elveszíti stabilitását. Ez elfogadhatatlan minőségű felületet eredményez.

Marási folyamatnál csak stabil stacionárius forgácsolás megengedett. Ennek elérése céljából határozzák meg a stabilitási térképet, amely megmutatja, hogy ez mely technológiai paraméterek mellett teljesül. A stabilitási térképről kiválaszthatók olyan technológiai paraméterek, amelyeknél nagy anyagleválasztási hányad érhető el stacionárius forgácsolási folyamat mellett, habár ilyenkor leggyakrabban a rezonancia-közeli gerjesztett rezgés lesz domináns, ami tervezhető felületi hibát okoz.

A kutatás célja, a megválaszolandó kérdések

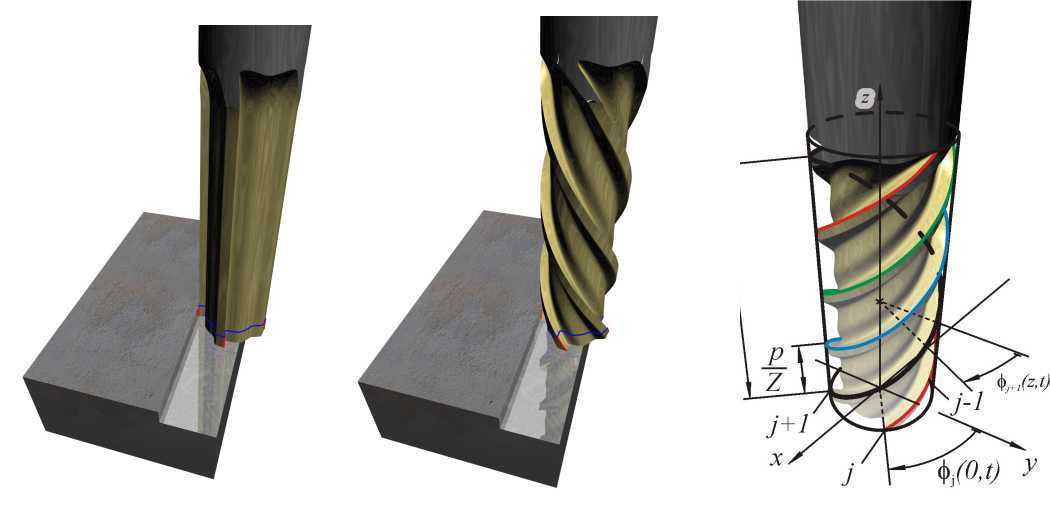
Az irodalomban használt módszerek többsége a marószerszámot általában egyenes élűnek tételezi fel, annak ellenére, hogy a szerszámok többsége csavart éllel rendelkezik. Kutatásunk egyik célja a csavart élű marószerszám analitikus módszerekkel történő pontosabb modellezése, valamint a megmunkált felület térbeli előállítása és a felület tulajdonságainak pontosabb leírása.  

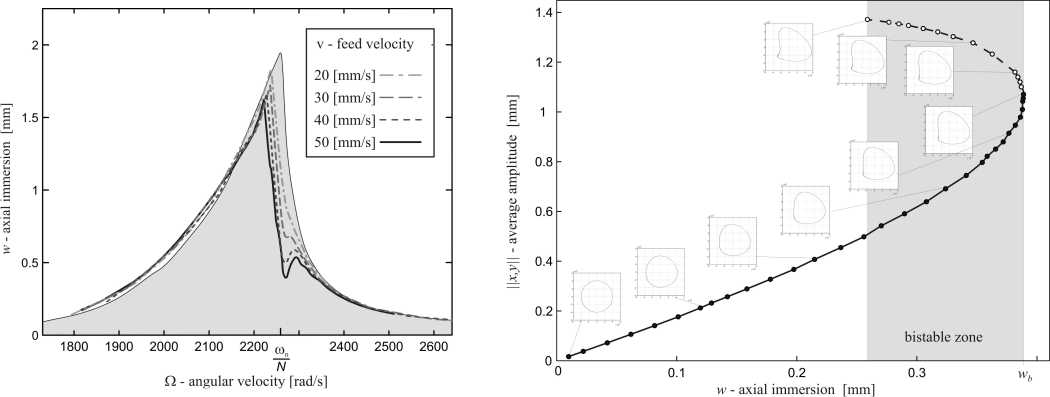
Eddigi kutatásaink alapján úgy találtuk, hogy bizonyos paramétereknél, rezonancia-közeli esetekben, a kialakult erő-gerjesztett rezgések nagysága összemérhető lehet a szerszámátmérővel. A marási modellek többsége ezt a rezgésamplitúdót általában elhanyagolja. Ezekben az egyszerűsített modellekben az erő-gerjesztett és az öngerjesztett rezgések egymástól függetlenül vizsgálhatók, mivel az egyenletekben megjelenő időkésés konstansnak tekinthető. Célunk a két rezgés együttes vizsgálata és a rezonancia közelében kialakult nagy rezgések stabilitási térképre gyakorolt hatásának elemzése.

A számítások során kimutattuk, hogy ez a hatás akkor jelentősebb, ha a rezgés sebességamplitúdója és a forgácsolási sebesség hasonló nagyságrendbe esnek. Kis fordulatszám esetén ez már kis rezgési amplitúdónál is bekövetkezhet, de ezekben az esetekben további hatások is meghatározó szerepet kapnak. Ezek közül a legjelentősebb a megmunkálási csillapítás, az úgynevezett „process-damping”, amelynek hatására a stabilitási határok eltolódnak a nagyobb axiális fogásmélység irányába. Kutatásunkban ennek leírására használt modelleket fejlesztettünk ki és elemeztünk.

Módszerek

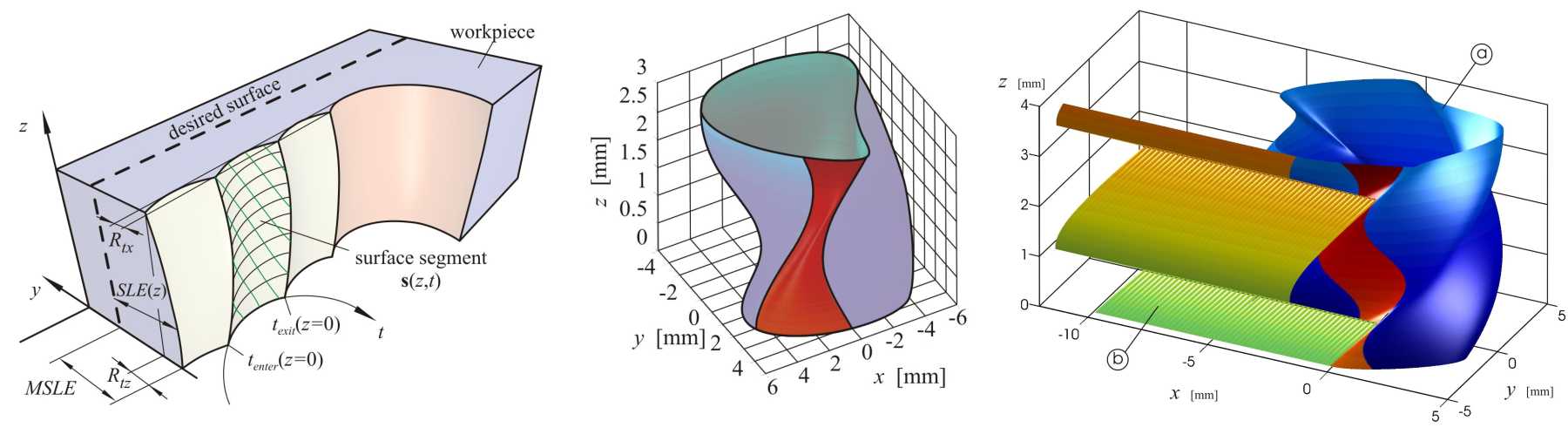
A csavart élű szerszám leírásánál figyelembe vettük a forgácsoló él térbeli alakját, vagyis azt, hogy az axiális koordináta függvényében az él a rezgés különböző fázisaiban lép kapcsolatba az anyaggal. Ennek hatására a síkbeli modelleknél alkalmazott felületi eltolódás, az úgynevezett „Surface Location Error” szintén változik az axiális koordináta mentén, ami térbeli mintázatot okoz a felületen. A forgácsoló erő számítása ebben az esetben egy időfüggő és változó határú integrálra vezet, amelyet analitikusan meg lehet határozni. Az így kapott mozgásegyenlet erő-gerjesztett periodikus mozgásait Fourier sorok segítségével állítottuk elő, és egy jellemző megmunkált térbeli felületszegmenst generáltunk. A felület megfelelő leírására három különböző paramétert alkalmaztunk: a maximális felületi eltolódást és az előtolási, illetve axiális irányban értelmezett felületi érdességet. A rendszer stabilitását az időben periodikus rendszerek leírására használt, az időkésleltetett egyenletekre általánosított Floquet elméleten alapuló szemi-diszkretizációs eljárással vizsgáltuk.

A rezonancia-közeli esetekben kialakuló rezgés figyelembevételekor a forgácsvastagság leírására egy összetettebb modellt kell alkalmazni. A pontosabb számításból kiderült, hogy a meghatározott időkésés függ a szerszám aktuális és múltbeli pozíciójától, azaz a megelőző él pályájától is. Ebben az esetben egy állapotfüggő időkésleltetett differenciálegyenletet kapunk, amely alapvetően nemlineáris, így az erő-gerjesztett és az öngerjesztett rezgéseket nem lehet külön kezelni. A nemlineáris viselkedés miatt a kialakult pályákat csak a saját kontinuitási algoritmusunkkal tudtuk vizsgálni. Az állapotfüggő időkésleltetés miatt bonyolult feladat a meghatározott pályák körüli linearizálás is, amely egyes esetekben szinguláris egyenletekre vezethet. A linearizálás után a pályákat és azok stabilitását az említett szemi-diszkretizációs eljárással már tudtuk vizsgálni.

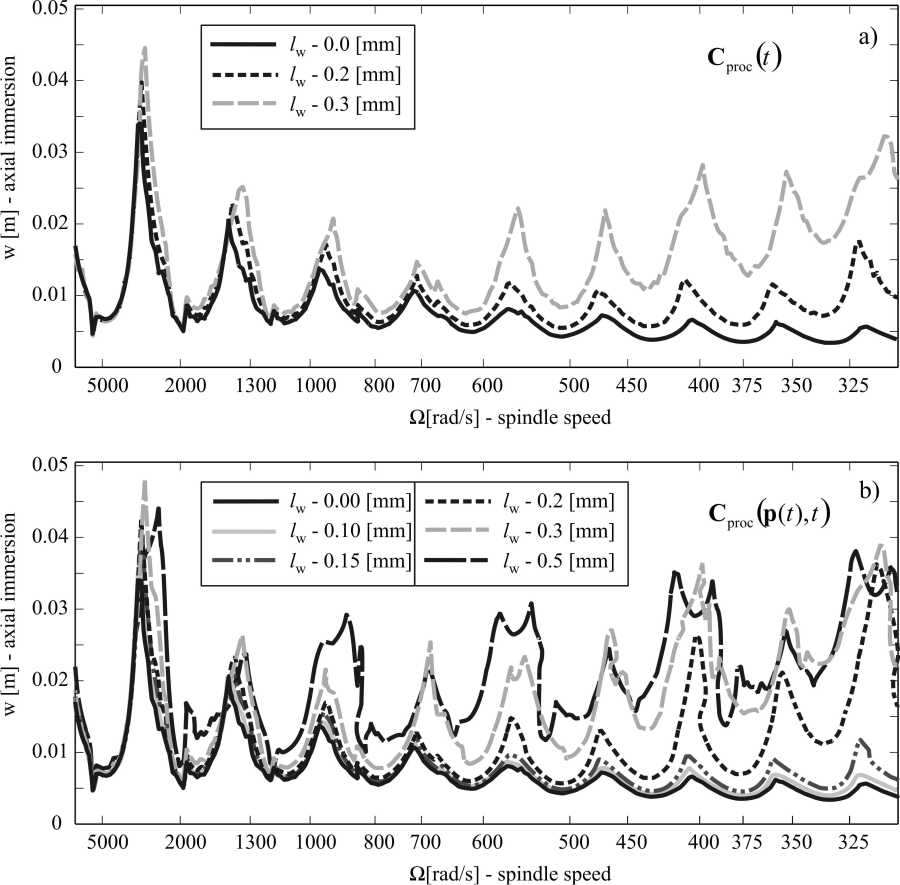
Kisebb fordulatszámú marás esetében figyelembe kell venni a megmunkálási csillapítást is. A stabilitási határok eltolódásának magyarázatára többféle modell is létezik. Az egyik legrégebbi módszer egy új viszkózus csillapítási tag bevezetése, amelynek nagysága lineárisan arányos az időkéséssel, azaz fordítottan arányos a fordulatszámmal. Az elméletből ismert, hogy ezt a csillapítást a hátlapon kialakuló rugalmas deformáció hatására fellépő száraz súrlódási erő kelti.

A rövid-regeneratív hatást leíró másik modellben a szerszám homloklapján lefutó forgács által keltett kis megoszló erőrendszert is figyelembe vesszük, ami egy folytonos (elkent) időkésésű matematikai modellhez vezet. Ezt a modell bonyolultsága miatt eddig főként esztergálási folyamatokra alkalmazták. Munkánk során egy olyan marási modellt vizsgáltunk, amelynek segítségével igazolni tudtuk, hogy a viszkózus csillapítási tag bevezetése a rövid-regeneratív hatás egyfajta elsőrendű közelítése. A javasolt modellben a csillapítási tag a szerszám sebességének szakaszonként konstans függvénye, ezáltal nemlineáris egyenleteket kaptunk, amelyeket a fentiekben leírt módszerrel tudtunk elemezni.

Eddigi eredmények

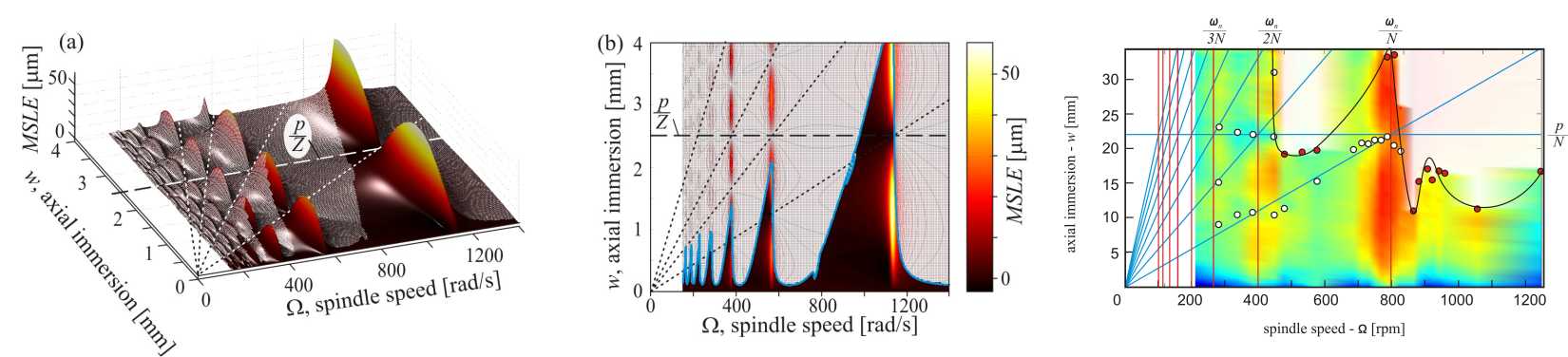
Stabil marás esetén meghatároztuk a munkadarab felületét csavart élű szerszám esetére. Új felületi paramétereket vezettünk be a térbeli alak jellemzésére. Legfontosabb felismerésünk, hogy meghatározott optimális axiális fogásmélység alkalmazása esetén egyszerre biztosítható igen jó felületi minőség és kis rezgési amplitúdó még rezonancia-közeli fordulatszám esetén is. Egyes optimális axiális fogásmélységek triviálisak, amikor is a forgácsoló erő konstans értékű, vagyis a fogásmélység egész számú többszöröse egy bekezdés magasságának. Találtunk nem triviális optimális axiális fogásmélységeket is, amelyek lineárisan függenek a fordulatszámtól. Rezonáns fordulatszám esetén ezek egyenletesen elosztva helyezkednek el a triviális axiális fogásmélységek között. Az analitikus eredményeket mérésekkel is validáltuk egy iparban is használt marógépen.

A stabilitási térképek részletes vizsgálatával megmutattuk, hogy a csupán a kis rezgéseket figyelembe vevő tradicionális modellek rezonancia-közeli fordulatszámok esetén túlbecsülhetik a stabilitási határokat. Az erőgerjesztett rezgések bifurkációs diagramjai alapján eddig szokatlan ’fold’ bifurkációt találtunk, amely bistabil tartományt hoz létre. Az ilyen paramétertartományokban a stacionárius marási folyamat nem globálisan stabil, azaz kismértékű zavarásra is tartós, nagy amplitúdójú rezgések alakulhatnak ki. Modellünk alkalmazhatóságának figyelembevételével meghatároztuk ennek a bistabil technológiai paraméterzónának a méretét. 

A kis fordulatszámú marási folyamatok leírására egy továbbfejlesztett, a megmunkálási csillapítást is figyelembe vevő modellt hoztunk létre. A hátlapon létrejövő kontakt érintkezési erőt a megkopott hátlap által összenyomott felület hozza létre. Ez az erő megadható egy sebességfüggő periodikus csillapítási mátrix segítségével. Megmutattuk, hogy a fenti modell az irodalomból ismert, rövid-regeneratív hatást tartalmazó modell elsőfokú közelítése, ami alapján belátható, hogy a modell pontatlan lehet nagyon alacsony vágási sebességek esetén, ahol a kialakult rezgés hullámhossza a hátlap kopásának nagyságrendjébe esik.

A stabilitási térképet különböző hátlapkopások esetén számítottuk ki, ezzel megmutatva, hogy a stabilitási határok mintázata változik növekvő kopás esetén. Ennek a jelenségnek magyarázatát adja az általunk bevezetett, idő- és sebességfüggő csillapítási mátrix.

Várható impakt, további kutatás

A csavart élű marószerszám esetén meghatározott nemtriviális optimális axiális fogásmélység számítása igen egyszerű és nagy gyakorlati jelentőséggel bír, mivel így rezonancia-közeli fordulatszámoknál is kis rezgések lépnek fel és jó felületi minőség alakul ki, ezzel lehetőséget adva nagy anyagleválasztási ráta elérésére, a megmunkálási idő csökkentésére, valamint a szerszám élettartamának növelésére.

A marási modellre alkalmazott állapotfüggő időkéséses egyenletek eredményei alapján új jelenségre, mégpedig egy bistabil tartomány megjelenésére hívtuk fel a figyelmet. Ez újabb, nem várt problémák forrása lehet, amelyek tisztázásához összetettebb mérésekre és a mélyebb fizikai okok feltárására lesz szükség.

A marási modellben a megmunkálási csillapítás alkalmazásával igyekeztük pontosítani a meglévő modelleket és felhívni a figyelmet arra, hogy a jelenség fizikai tartalma a rövid regenerációs hatáson alapul, amely matematikailag ugyan összetettebb, de pontosabb és megbízhatóbb eredményekre vezet.

További cél, hogy az eddigi modellek összeépítésével igen általános és tág technológiai paramétertartományban érvényes modellt kapjunk, valamint hogy mérésekkel támasszuk alá az egyes jelenségek modellezését.

Saját publikációk, hivatkozások, linkgyűjtemény

Folyóiratcikkek

Bachrathy D, Stepan G, Turi J: State dependent regenerative effect in milling processes, Computational and Nonlinear Dynamics  (2010), benyújtva.

Bachrathy D, Insperger T, Stepan G: Surface properties of the machined workpiece for helical mills, Machining Science and Technology 13 (2009) 227 – 245. DOI 10.1080/10910340903012167.

Bachrathy D, Mészáros I: Nagypontosságú kemény esztergálás dinamikai vizsgálata megszakított felületek esetén, Gépgyártás XLIX:(4 – 5) (2009) 47 – 53. oldal

Konferenciák

Bachrathy D, Mészáros I: Optimal cutting speeds, entrance and exit force in interrupted high precision hard turning, 7th International CIRP Conference on Intelligent Computation in Manufacturing Engineering (ICME). (Capri, Olaszország, 2010) 1 – 4. oldal

Bachrathy D, Stepan G: Time-periodic velocity-dependent process damping in milling processes, 2nd International CIRP Process Machine Interaction (PMI) Conference. (Vancouver, Kanada, 2010) 1 – 12. oldal, ISBN: 978-0-9866331-0-2

Bachrathy D, Reith M J, Mészáros I: Optimal cutting speeds and surface prediction in interrupted high precision hard turning, 7th International Conference on Mechanical Engineering. (Budapest, 2010) 241 – 246. oldal, ISBN: 978-963-313-007-0

Bachrathy D, Mészáros I: Dynamical problems in interrupted high precision hard turning, LAMDAMAP 2009: 9th International Conference and Exhibition on Laser metrology, machine tool, CMM and robotic performance. (London, Anglia, 2009) 357 – 367. oldal, ISBN:978-0-9553082-7-7

Bachrathy D, Stépán G: Bistable parameter region caused by velocity dependent, 12th CIRP Conference on Modelling of Machining Operations. (San Sebastian, Spanyolország, 2009) 867 – 871. oldal, ISBN:978-84-608-0866-4

Mészáros I, Bachrathy D, Farkas B: Dynamical problems in high precision hard cutting, Manufacturing 2008: Biannual 19th International Conference on Manufacturing. (Budapest, 2008) 18 – 24. oldal, ISBN:978-963-9058-24-8

Bachrathy D, Stépán G: Experimental Setup for Fast Stability Chart Reconstruction of Milling Processes,

6th International Conference on Mechanical Engineering. (Budapest, 2008) 1 – 7. oldal, ISBN:978-963-420-947- 8

Bachrathy D, Stepan G: Efficient experimental detection of milling stability boundary and the optimal axial immersion for helical mills, in Proceedings of the International Multi-Conference on Engineering and Technological Innovation, (Orlando, Florida, 2008) I. kötet, 7 – 11. oldal, ISBN: (13) 978-1-934272-43-5

Bachrathy D, Homer M, Insperger T, Stepan G: Surface location error for helical mills, 6th International Conference on High Speed Machining (San Sebastian, Spanyolország, 2007) (CD-ROM) 379 – 384. oldal

Bachrathy D, Stepan G: Good surface properties at efficient technological parameters in milling process, 24th Danubia-Adria Symposium (Nagyszeben, Románia, 2007) 45 – 46. oldal, ISBN:978-973-739-456-9

Bachrathy D, Insperger T, Stépán G: Felületi minőség számítása csavart élű szerszámmal történő marás során, X. Magyar Mechanikai Konferencia. (Miskolc, 2007) 1 – 4. oldal

Bachrathy D, Stepan G: Surface error for helical mills, 6th International Congress on Industrial and Applied Mathematics (Zürich, Svájc, 2007) (CD-ROM: IC/MT(MP669)1083/151) 1 – 6. oldal

Linkgyűjtemény

MTA-BME Gépek és Járművek Dinamikája Kutatócsoport

Műszaki Mechanikai Tanszék

Saját Youtube-videók:

Experimental validation of the "appropriate axial immersions".

Representation of the milling process created by a helical futed tool.

Representation of the period doubling motion of the milling tool.