Doctoral School of Information Science and Technology

Department of Telecommunications

Supervisor: Sandor Imre, DSc

Using Quantum-Based Solutions in Satellite Communications

Introducing the research area

Quantum computing offers revolutionary solutions in the field of computer sciences, applying tools of quantum physics, which are incomparably numerous than those of classical physics. Although quantum computers merely promise applications for the far future, a few algorithms are already available for solving problems otherwise difficult to handle with traditional computers. Today's telecommunication requires large amount of data transfer via satellites. An interesting way of dealing with this problem might be using quantum communication. Unlike the optical cable-based, wired quantum solutions, quantum satellite communication requires a free-space channel, which is affected by various physical factors. Over the last years, we have developed a mathematical model for examining satellite quantum communications. We have analysed the redundancy-free quantum channel and developed redundancy-free quantum codes.

Brief introduction of the research place

Mobile Communication and Computing Laboratory at BME Department of Telecommunications has been working on wireless and mobile systems for more than 10 years. Under the leadership of Dr. Imre Sándor, several members of the laboratory have started dealing with quantum informatics and numerous publications have been completed since 2003. At present, and three PhD dissertations are in process.

History and context of the research

In 1965, Gordon Moore studied the number of transistors that can be placed inexpensively on an integrated circuit[1]. The big question is that how long this trend – i.e the increase in the number of transistors – is going to continue?

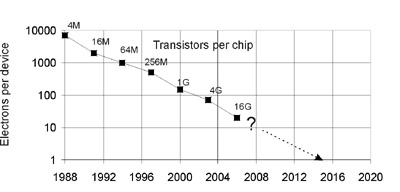
Researches offer different solutions to this problem, e.g. use of parallel computers, DNS-technology or informatics based on quantum mechanics. Why quantum mechanics? To allocate more transistors on an integrated circuit of a given size, the size of individual transistors have to be reduced. At one point, we will cross the borderline of atomic dimensions, where classical Ebers-Moll equals are not valid anymore, and quantum mechanical models have to be used instead [2].

Why are quantum-based approaches better than the classical ones? The power of quantum parallelism allows us to solve classically complex problems during a short period of time. Grover-algorithm provides more efficient searches in unsorted databases [1]. We can build different quantum circuits and decrypt the keys of RSA with the help of Shor-algorithm[2]. Quantum cryptography provides new ways of transmitting information securely (BB84 and B92 protocols) [3]. In quantum teleportation we use entangled pairs to transport information between two points [4].

Aim of the research

Free-space Quantum Key Distribution (QKD) was first implemented over an optical path of about 30 cm in 1991 [5]. In 2002, a research group demonstrated that free-space QKD is possible in daylight [6]. In 2006, the distance was further extended to 144 km by an international research group [7]. In 2008, the European Space Agency named the quantum-based satellite communication as one of the most important targets for the next five years. A European consortium aims at establishing a space-to-Earth quantum-based communication experiment from the International Space Station [8].

Free-space quantum communication can be extended to ground-to-satellite or satellite-satellite quantum communication [9]. One of the main advantages of using space for future quantum communication is achieving the level of loss-free and distortion-free optical communication. We have examined two different protocols – the superdense coding [1] and the BB84 [3].

Another interesting question is related to quantum error correction. Currently many techniques are introduced but in these proposals redundancy is required for successful error correction. If we could use redundancy-free solutions, they would be very useful in the long-distance aerial communication, eliminating the need for redundant error correction codes used nowadays.

Methods

At present, using optical QKD is limited to a distance of appr. 100 km, however, free-space quantum cryptography makes it possible transmitting photons over long distances. We examined the physical properties of the Earth-space and space-space channels to give some prescriptions about the possible losses and to give some useful ideas about the implementation of such a channel [10, 11]. We also developed an analytical model which describes one photon’s (or a few photons’) behavior to simulate the communication process over a satellite quantum channel. Our model enables us to analyze and determine the parameter requirements to the implementation of a satellite quantum channel for Earth-satellite and satellite-satellite communication.

In a best case scenario of superdense coding, Alice and Bob already share an entangled qubit pair, and thus every qubit sent by Alice and arriving at Bob’s detector carries two bits of information. In the statistical sense, the protocol is not worthwhile if more than half of the qubits sent by Alice is not detected (in other words, if the transmittance is lower than 0.5). In this case, strong signals and classical protocols perform better.

The most famous flexible asymmetrical protocol is the BB84 protocol. It is important to examine the performance and limits of cryptography based on BB84 in various environments as well as to know the noise parameters of the quantum channel, as errors appearing in the received quantum bits allow us to discover an eavesdropper.

We also used the analytical methods to study the free-space quantum channel. Analytical solutions were applied for constructing error coding methods to support redundancy-free approaches.

Results

Based on our mathematical models, we were able to examine selected parameters of quantum satellite communication. According to our results, the distance between two satellites should be maximum 15,000 km to handle a successful BB84. These results show that we can realize quantum communication over intercontinental distances. However, after analyzing of LEO (Low Earth Orbit) and GEO (Geostationary Earth Orbit) satellite orbit, we can say that a BB84 supported equipment running on a LEO satellite cannot reach a GEO satellite.

Another important question is how fast the satellites can exchange keys with the BB84 depending on the distances. (The BB84 key distribution protocol was published by Charles H. Bennett and Gilles Bassard in 1984. The algorithm working in wired system is a commercial product. Efficiency of the free-space quantum channel is examined by this protocol.) We have shown that the LEO orbits are better for the BB84. However, we extended our examinations to the superdense coding algorithms, as well. (In superdense coding algorithm, we need to send only one quantum bit instead of two classical bits.) According to our results, superdense coding in a best case scenario is only worthwhile in clear weather, at low zenith angles and for large detector mirror sizes.

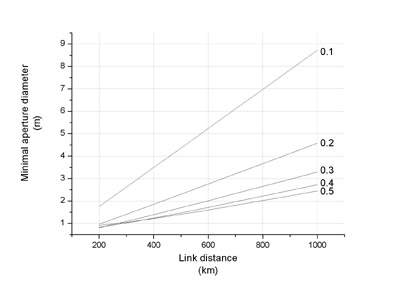
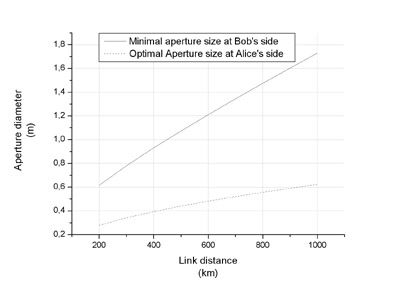
In another research, we would like to provide error correction by sending certain amount of qubits over a noisy quantum channel. The qubits are independent and each contains information that needs to be processed. We developed different redundancy-free solutions for free-space quantum communication.

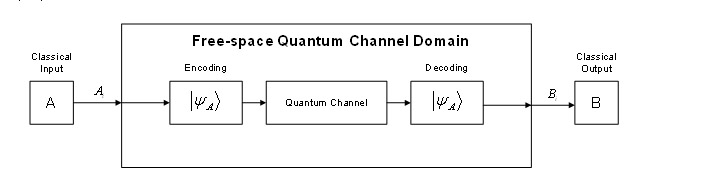
We started with a special unitary channel, where the information itself was classical, coded into qubits. The channel transforms a unitary transformation with p probability and an identity transformation with 1-p probability. We can construct an error coding description in which the classical states are coded into the eigenvectors of the matrix of the unitary channel. We have shown that this error-coding construction leads to a redundancy-free solution because we can restore one quantum bit sent over the channel without any other (redundant) information.

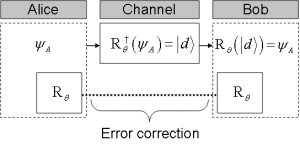
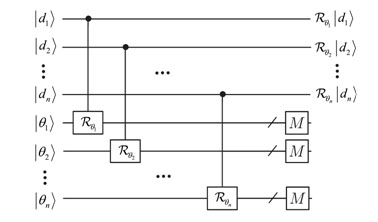
In the next step, we considered the redundancy-free implementation of a unitary error correcting operator. The protocol achieves the redundancy-free quantum communication using local unitary operations and unitary matrices. Our research is important because using these redundancy-free techniques effective capacity of the satellite link could be increased..

Expected impact and further research

Examining the connection of quantum informatics and satellite communication back in 2003 meant starting to deal with a field which gained more and more importance. Our research area is even more interesting because it combines results of mathematical modeling, information theory and engineering.
We have received more article review requests. In this year we were invited to submit two different book chapters.

In our further research, we would like to study the way can use entangled pairs in redundancy-free coding. In another research topic, we examine how we can improve self-adapting communication networks through the application of quantum-informatics-based solutions.

Publications, references, links

Publications

International journal articles

Laszlo Bacsardi
Satellite Communication Over Quantum Channel
ACTA ASTRONAUTICA 61:(1–6) pp. 151–159. (2007)

Laszlo Bacsardi
Using Quantum Computing Algorithms in Future Satellite Communication
ACTA ASTRONAUTICA 57:(2–8) pp. 224–229. (2005)

International book chapters

Laszlo Bacsardi, Sandor Imre
Quantum-Based Information Transfer in Satellite Communication
Book: „Satellite Communications”, ISBN 978-953-7619-X-X, Sciyo (accepted, to appear)

Laszlo Bacsardi, Laszlo Gyongyosi, Marton Berces, Sandor Imre
Quantum Solutions for Future Space Communication
Book: „Quantum Computers”, Nova Science Publishers (accepted, to appear)

Laszlo Bacsardi, Laszlo Gyongyosi, Sandor Imre
Solutions for Redundancy-Free Error Correction in Quantum Channel
LECTURE NOTES OF THE INSTITUTE FOR COMPUTER SCIENCES SOCIAL-INFORMATICS AND TELECOMMUNICATIONS ENGINEERING 36: pp. 117–124. (2010)

International conference papers

Mate Galambos, Laszlo Bacsardi, Sandor Imre
Modeling and Analyzing the Quantum-Based Earth-Satellite and Satellite-Satellite Communications
International Astronautical Congress 2010 (accepted)

L. Bacsardi, L. Gyongyosi, S. Imre
Using Redundancy-free Quantum Channels for Improving the Satellite Communication
In: Proceedings CD of 2nd International ICST Conference on Personal Satellite Services. Rome, Italy, 2010.02.04–2010.02.05., pp. 1–14. Paper 8560.

L Bacsardi, L Gyongyosi, S Imre
Solutions for Redundancy-Free Error Correction in Quantum Channel
In: Proceedings CD of 1st International ICST Conference on Quantum Communication and Quantum Networking. Vico Equense, Italy, 2009.10.26–2009.10.30., Gent: pp. 1–8. Paper 8077. (ISBN: 978-963-9799-83-7)

L. Bacsárdi, M. Bérces, S. Imre
Redundancy-Free Quantum Theory-Based Error Correction Method in Long Distance Aerial Communication.
In: 59th International Astronautical Congress, IAC Proceedings 2008. Glasgow,Great Britain, 2008.09.29–2008.10.03. pp. 1–7. Paper IAC-08-B2.4.8.

Hungarian journal articles

László Bacsárdi, Máté Galambos, Sándor Imre
Quantum channel in Earth-satellite and satellite-satellite communications
HÍRADÁSTECHNIKA LXV:(3–4.) pp. 23–29. (2010)

Scientific lectures (in Hungarian)

László Bacsárdi
Teleporting with the speed of light – adventures in the world of quantum informatics
Future's techniques, techniques from the future, Sopron, Apr 14, 2010

László Bacsárdi, Sándor Imre
The mistery of the root NOT gate - will have Mr. Moore a good night on tomorrow?
Puskás Tivadar Távközlési Technikum, Budapest, March 29, 2010

László Bacsárdi
Using quantum informatics in space telecommunication - could ET make a home-call faster than the speed of light?
Gyula Fényi Astronomical Open University, Sopron, Nov 23, 2007

Links

Website of our university lecture - Quantum Informatics and Communications

Selected web portals

Quantiki
Virtual Journal of Quantum Information
The International Nanoscience Communicity

Quantum companies

id Quantique (sells Quantum Key Distribution products)
MagiQ Technologies (sells quantum devices for cryptography)
Quintessence Labs Solutions (based on continuous wave lasers)

References

[1] S. Imre, B. Ferenc, ‘Quantum Computing and Communications: An Engineering Approach’, (Wiley, 2005)
[2] Michael A. Nielsen, IsaacL. Chuang, ’Quantum Computation and Quantum Information’ (Cambridge University Press, 2000)
[3] Charles H. Benett, Gilles Bassard, ’Quantum Chryptography: Public Key Distribution and Coin Tossing’, Internation Conference on Computers, Systems & Signal Processing, Bangalore, India (December 10–12, 1984)
[4] Teleporting an Unknown Quantum State via dual Classical and Einstein-Podolsky-Rosen Channels, C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W. K. Wooters, (Phys. Rev. Lett, vol. 70, n 13, pp. 1895, March 1993)
[5] C. H. Bennett et al., Lecture Notes In Computer Science 473, 253 (1991).
[6] Richard J. Hughes, Jane E. Nordholt, Derek Derkacs and Charles G. Peterson, Practical free-space quantum key distribution over 10 km in daylight and at night, (New Journal of Physics 4 (2002) 43.1–43.14 )
[7] Tobias S-Manderbach, et al., ’Experimetal Demostration of Free-Space Decoy-State Quantum Key Distribution over 144km’, Phys. Rev. Lett. 98, 010504 (2007)
[8] Josep Maria Predigues Armengol, et al., ’Quantum Communications at ESA: Towards a space experiment on the ISS’, Acta Astronautica 63, 165–178 (2008)
[9] L. Bacsardi, Satellite Communication Over Quantum Channel., Acta Astronautica 61:(1–6) pp. 151–159, 2007
[10] Larry C. Andrews and Ronald L. Phillips, ’ Laser Beam Propagation through Random Media’, (SPIE Press Book, 2005)
[11] C. Bonato et al., ’Polarization transformation induced on qubits in a Space-to-Earth quantum communication link’, Quantum Electronics and Laser Science Conference (2007)

Source of the figures: Wikipedia, free-to-use pictures, official logo of the Mobile Communication and Computing Laboratory, self-made figures.