
|
BMe Kutatói pályázat |

|
Informatikai Tudományok Doktori Iskola
Híradástechnikai Tanszék
Témavezető: Dr. Imre Sándor
Kvantuminformatika alkalmazása űrtávközlésben
A kutatási téma néhány soros bemutatása
 Az
1980-as évek közepétől folynak olyan kutatások, amelyek a kvantummechanikát és
az informatikát próbálják közös nevezőre hozni. Habár a kvantumszámítógépek csak
a távoli jövő eszközei lesznek, már léteznek algoritmusok olyan problémák
megoldására, amelyek a hagyományos számítógéppel nehezen kezelhetők. A
műholdas kommunikáció során hatalmas információigény lép fel, ezért érdemes
megvizsgálni, hogyan tudnánk használni kvantummechanikai alapelveken működő
kvantuminformatikai algoritmusokat ezekben a kommunikációs folyamatokban.
Az
1980-as évek közepétől folynak olyan kutatások, amelyek a kvantummechanikát és
az informatikát próbálják közös nevezőre hozni. Habár a kvantumszámítógépek csak
a távoli jövő eszközei lesznek, már léteznek algoritmusok olyan problémák
megoldására, amelyek a hagyományos számítógéppel nehezen kezelhetők. A
műholdas kommunikáció során hatalmas információigény lép fel, ezért érdemes
megvizsgálni, hogyan tudnánk használni kvantummechanikai alapelveken működő
kvantuminformatikai algoritmusokat ezekben a kommunikációs folyamatokban.
A kvantuminformatikai algoritmusok szabadtéri megvalósítása még a kísérleti
és kutatási fázisnál tart. Az optikai kábelen megvalósított alkalmazásoktól
eltérően ezekben az esetekben egy szabadtéri csatornára van szükség, amelyet
számos fizikai tényező befolyásol. Kutatásunkban a műholdas kvantumkommunikáció
modellezésével, a redundanciamentes kvantumcsatornával és a redundanciamentes
kvantumalapú kódolással foglalkozunk.
A kutatóhely rövid bemutatása
 A
BME Híradástechnikai Tanszéken működő Mobil Távközlési és Informatikai Laboratórium már
több mint 10 esztendeje foglakozik vezeték nélküli és mobil rendszerekkel. Dr.
Imre Sándor vezetésével a labor néhány tagja a kvantuminformatika
területe felé nyitott – 2003 óta számos nemzetközi publikáció, TDK-dolgozat és
diplomaterv született, és jelenleg is három PhD-disszertáció készül.
A
BME Híradástechnikai Tanszéken működő Mobil Távközlési és Informatikai Laboratórium már
több mint 10 esztendeje foglakozik vezeték nélküli és mobil rendszerekkel. Dr.
Imre Sándor vezetésével a labor néhány tagja a kvantuminformatika
területe felé nyitott – 2003 óta számos nemzetközi publikáció, TDK-dolgozat és
diplomaterv született, és jelenleg is három PhD-disszertáció készül.
A kutatás történetének, tágabb kontextusának bemutatása
A Gordon Moore által 1965-ben megfigyelt törvényszerűség, a Moore-törvény napjainkban is működik. Eszerint a processzorok teljesítménye 18 havonta megduplázódik, ráadásul folyamatos méretcsökkenést is megfigyelhetünk az integrált áramkörök világában [1].
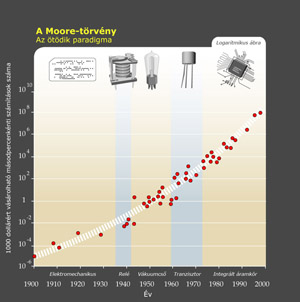
Sokakban felmerül a kérdés, hogy meddig folytatódhat ez a méretcsökkenés. Az egyik
lehetséges megoldást a kvantummechanikai
elveken alapuló informatika, a kvantuminformatika kínálja. (Más megoldás
lehet például az elosztott rendszerek alkalmazása vagy a DNS-alapú
számítástechnika.) A tranzisztorok méretét folyamatosan csökkenteni kell ahhoz, hogy ugyanakkora (vagy egyre kisebb) alapterületű lapkára egyre több tranzisztort zsúfoljunk. Egy ponton át fogjuk lépni az atomi
mérettartományt, és ebben a világban már nem lesznek érvényesek a klasszikus
fizikában használt Ebers-Moll-egyenletek,
hanem kvantummechanikai modelleket kell alkalmazni [2].
 Mivel
nyújtanak többet a kvantumalapú eszközök, mint a klasszikus informatika által
kínált lehetőségek? A kvantumpárhuzamosság elvének kihasználásával könnyen
elvégezhetjük a nagy számításigényű műveleteket (pl. Deutsch-Jozsa-algoritmus),
kvantumalapú prímfaktorizációt valósíthatunk meg (pl. a Shor-algoritmus
segítségével) [2]. A klasszikus módszereknél hatékonyabban tudunk adatbázisban
keresni (Grover-algoritmus),
különböző kvantumkapukat és kvantumáramköröket építhetünk, szupersűrű kódolást
alkalmazhatunk, sőt még kvantumalapú
Fourier-transzformációt is tudunk végezni [1]. A kvantumkulcsszétosztás
protokolljai (BB84, B92) révén biztonságos módon
tudunk kulcsot szétosztani [3], az összefonódás
jelensége miatt pedig képesek vagyunk információt teleportálni (kvantumteleportáció)
[4].
Mivel
nyújtanak többet a kvantumalapú eszközök, mint a klasszikus informatika által
kínált lehetőségek? A kvantumpárhuzamosság elvének kihasználásával könnyen
elvégezhetjük a nagy számításigényű műveleteket (pl. Deutsch-Jozsa-algoritmus),
kvantumalapú prímfaktorizációt valósíthatunk meg (pl. a Shor-algoritmus
segítségével) [2]. A klasszikus módszereknél hatékonyabban tudunk adatbázisban
keresni (Grover-algoritmus),
különböző kvantumkapukat és kvantumáramköröket építhetünk, szupersűrű kódolást
alkalmazhatunk, sőt még kvantumalapú
Fourier-transzformációt is tudunk végezni [1]. A kvantumkulcsszétosztás
protokolljai (BB84, B92) révén biztonságos módon
tudunk kulcsot szétosztani [3], az összefonódás
jelensége miatt pedig képesek vagyunk információt teleportálni (kvantumteleportáció)
[4].
A kutatás célja, a megválaszolandó kérdések.
 Habár a kvantumszámítógép
még a távoli jövő eszköze, már most léteznek olyan megoldások, amelyek
segítségével kvantum módon oszthatunk szét kulcsokat, az optikai
kábeleket használó megoldások azonban csak korlátozott távolságban működnek. Az első
szabadtéri kulcsszétosztással 1991-ben találkozhattunk, amit először
egy 30 cm-es szakaszon sikerült megvalósítani [5]. 2004 januárjában már egy 9,81 km-es
távolságon végzett sikeres kísérletről számoltak be [6], 2006-ban egy európai
kutatócsoport 144 km-es távolságon valósította meg mindezt [7]. 2008-ban az Európai
Űrügynökség a következő öt év egyik legfontosabb áttörésének jelölte meg a
kvantumalapú űrkommunikáció sikeres gyakorlati megvalósítását. Jelenleg többen
is azon dolgoznak, hogy a Nemzetközi
Űrállomással tudjanak a Földről kvantumalapú kapcsolatot létesíteni
[8].
Habár a kvantumszámítógép
még a távoli jövő eszköze, már most léteznek olyan megoldások, amelyek
segítségével kvantum módon oszthatunk szét kulcsokat, az optikai
kábeleket használó megoldások azonban csak korlátozott távolságban működnek. Az első
szabadtéri kulcsszétosztással 1991-ben találkozhattunk, amit először
egy 30 cm-es szakaszon sikerült megvalósítani [5]. 2004 januárjában már egy 9,81 km-es
távolságon végzett sikeres kísérletről számoltak be [6], 2006-ban egy európai
kutatócsoport 144 km-es távolságon valósította meg mindezt [7]. 2008-ban az Európai
Űrügynökség a következő öt év egyik legfontosabb áttörésének jelölte meg a
kvantumalapú űrkommunikáció sikeres gyakorlati megvalósítását. Jelenleg többen
is azon dolgoznak, hogy a Nemzetközi
Űrállomással tudjanak a Földről kvantumalapú kapcsolatot létesíteni
[8].
Kutatásunk célja, hogy a kvantumkommunikáció alkalmazásával a műholdas
kommunikációt (beleértve az űrtávközlést)
hatékonyabbá tegyük [9]. A műholdas kommunikáció azért érdekes számunkra, mert az
űrben a veszteségek sokkal kisebbek, mint akár a legjobb minőségű optikai
kábelben, így remélhetőleg nagyobb távolságban lehet megvalósítani ugyanazokat a
protokollokat, amelyeket a földön már sikerrel kipróbáltak. Két fontos protokollt
vizsgálunk – egyik a szupersűrűségű
tömörítés [1], másik pedig a BB84
kulcsszétosztó algoritmus [3].
További érdekes kérdés, hogy a két protokoll mellett milyen egyéb kódolási
eljárásokat tudunk alkalmazni, és léteznek-e olyan megoldások, amelyekkel redundáns adatok használata nélkül tudunk hibamentes átvitelt garantálni.
Módszerek
 A jelenleg létező technológiákra építő számításaink
segítségével vizsgáljuk a kvantumalapú űrtávközlés megvalósíthatóságát és
teljesítőképességét. Analitikus módon megvizsgáltuk az űr-föld és űr-űr
csatornák fizikai tulajdonságait [10, 11], és kidolgoztunk egy saját matematikai
modellt, amely alkalmas egyetlen (vagy néhány) fotonból álló jel viselkedésének
leírására, és így modellezni tudtuk az űrbeli kvantumkommunikáció
folyamatát.
A jelenleg létező technológiákra építő számításaink
segítségével vizsgáljuk a kvantumalapú űrtávközlés megvalósíthatóságát és
teljesítőképességét. Analitikus módon megvizsgáltuk az űr-föld és űr-űr
csatornák fizikai tulajdonságait [10, 11], és kidolgoztunk egy saját matematikai
modellt, amely alkalmas egyetlen (vagy néhány) fotonból álló jel viselkedésének
leírására, és így modellezni tudtuk az űrbeli kvantumkommunikáció
folyamatát.
Szupersűrű kódolás
esetén fontos tudni, hogy a transzmittancia (vagyis annak valószínűsége, hogy
egy Aliz által elküldött bit megérkezik Bob detektorához) milyen helyzetben
kisebb, mint 0,5, mivel ilyenkor nem érdemes a protokollt alkalmazni, hiszen
hiába lesz a kvantumbitek által átvihető információmennyiség duplája annak, amit
klasszikus esetben várnánk, ha a biteknek több mint a fele elvész. BB84
protokoll esetén szintén fontos, hogy ismerjük a csatorna veszteségeit és
torzító hatását, hiszen a kommunikációban bekövetkező hibákból következtethetünk
a támadó esetleges jelenlétére, így ha a hibás bitek száma meghalad egy bizonyos korlátot,
a csatorna már nem biztonságos.
Analitikus módszereket alkalmaztunk akkor is, amikor a szabadtéri csatornát
kódolás szempontjából vizsgáltuk, és olyan hibajavító eljárásokat konstruáltunk,
amelyekkel redundanciamentes kódolást valósíthatunk meg.
Eddigi eredmények
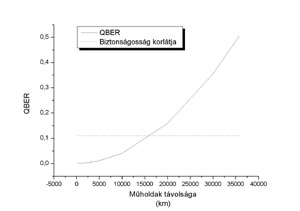
Matematikai modellünk segítségével megvizsgáltuk a kvantumalapú műholdas
kommunikáció gyakorlati megvalósításának bizonyos paramétereit. Vizsgálataink
megmutatták, hogy a biztonságos kommunikáció korlátja nagyjából 15 000 km, vagyis a két
műhold maximum ennyire távolodhat el egymástól, hogy a BB84 protokoll
segítségével még biztonságos kommunikációt tudjanak folytatni. Ez alapján
látható, hogy műholdas kvantumkommunikációval akár interkontinentális
távolságokat is át lehet hidalni, azonban az alacsony, úgynevezett LEO
(Low Earth Orbit – alacsony Föld körüli pálya) műholdas pályák és
geostacionárius GEO
(Geostationary Earth Orbit – geostacionárius Föld körüli pálya) pályák közötti
körülbelül 35 000 km-es távolságból látszik, hogy még egy
alacsonyan keringő műhold sem képes elérni egy geostacionárius pályán
mozgót.
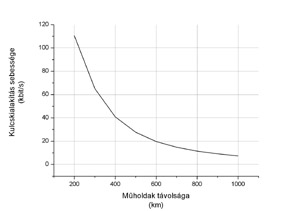
További fontos kérdés, hogy a műholdak milyen sebességgel képesek kulcsot kialakítani a BB84 protokoll segítségével a távolság függvényében. (A BB84 kulcsszétosztó protokollt Charles H. Bennett és Gilles Bassard 1984-ben publikálta. Vezetéken működő változatai kereskedelmi forgalomban kaphatók, és a szabadtéri kvantumkommunikáció hatékonyságát is ezzel a protokollal vizsgálják.) Munkánkból az derült ki, hogy ebben az esetben is az alacsonyabb műholdpályák előnyösebbek. Vizsgálatainkat azonban nemcsak a BB84 protokollra végeztük el, hanem kiterjesztettük a szupersűrűségű kódolásra is. (A szupersűrűségű tömörítés esetén két klasszikus bit helyett csak egyetlen kvantumbitet kell átküldeni.)
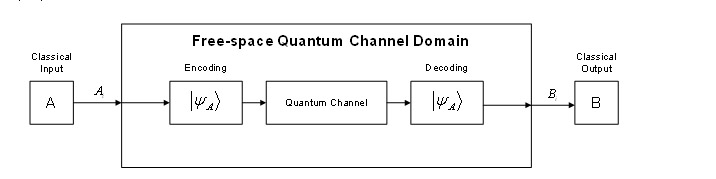
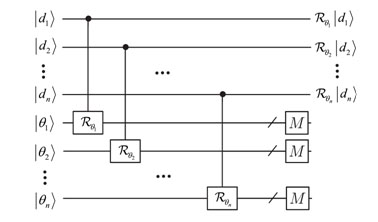
A redundanciamentes hibakódolással foglalkozó vizsgálatainkat egy speciális esettel kezdtük. Legyen adott egy olyan kvantumcsatorna, amely p valószínűséggel unitér transzformációt hajt végre a rajta átküldött biteken, 1-p valószínűséggel pedig nem változtatja. Ha egy unitér kvantumcsatornán az átküldésre szánt klasszikus információt úgy kódoljuk kvantumbitekbe, hogy azok a csatorna mátrixának sajátvektorai legyenek, akkor hibakódolást tudunk megvalósítani. Megmutattuk, hogy ez a konstrukciós eljárás egyben egy redundanciamentes hibakódolást valósít meg. A kiindulási feltételeket tágabbra választva hibakódolás eljárást dolgoztunk ki egy általánosabb kvantumcsatornára, lokális unitér operátorok segítségével.
Várható impakt, további kutatás
A kvantuminformatika és az űrtávközlés kapcsolatának vizsgálatával 2003-ban
egy olyan területtel kezdtünk el foglalkozni, amely napjainkra egyre nagyobb
figyelmet kap. Kutatási területünk azért is érdekes, mert a matematikai
modellezés, az információelmélet és a mérnöki tevékenység eredményeit ötvözi.
Egyre több cikkbírálatra kérnek fel, idén két könyvfejezet elkészítésére is
meghívást kaptunk. Jelenleg egy nemzetközi, kvantumkommunikációval foglalkozó
konferencia szervezésére pályázunk.
A továbbiakat tekintve érdekes feladatnak tartjuk annak vizsgálatát, hogy miként
tudjuk felhasználni az összefonódott párokat a redundanciamentes kódolásban. Egy
másik kvantuminformatikai kutatási vonalon pedig azt vizsgáljuk, hogy miként lehet
az önszerveződő vezeték nélküli hálózatok hatékonyságát növelni kvantuminformatikai megoldásokkal.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája
Nemzetközi folyóiratcikkek
Laszlo Bacsardi: Satellite Communication Over Quantum
Channel.ACTA ASTRONAUTICA 61:(1 – 6) 151 – 159. oldal
(2007)
Laszlo Bacsardi: Using Quantum Computing Algorithms
in Future Satellite Communication.ACTA ASTRONAUTICA 57:(2 – 8) 224-229.
oldal (2005)
Nemzetközi könyvfejezetek
Laszlo Bacsardi, Sandor Imre: Quantum Based Information Transfer in
Satellite Communication.
Könyv: „Satellite Communications”, ISBN
978-953-7619-X-X, Sciyo (elfogadott, megjelenés alatt)
Laszlo
Bacsardi, Laszlo Gyongyosi, Marton Berces, Sandor Imre: Quantum Solutions
for Future Space Communication. Könyv: „Quantum Computers”, Nova Science
Publishers (elfogadott, megjelenés alatt)
Laszlo Bacsardi,
Laszlo Gyongyosi, Sandor Imre: Solutions for Redundancy-Free Error Correction
in Quantum Channel.LECTURE NOTES OF THE INSTITUTE FOR COMPUTER SCIENCES
SOCIAL-INFORMATICS AND TELECOMMUNICATIONS ENGINEERING 36: 117 – 124. oldal
(2010)
Nemzetközi konferenciacikkek
Mate Galambos, Laszlo Bacsardi, Sandor Imre: Modeling and Analyzing
the Quantum Based Earth-Satellite and Satellite-Satellite
Communications.International Astronautical Congress 2010
(elfogadott)
L. Bacsardi, L. Gyongyosi, S. Imre: Using
Redundancy-free Quantum Channels for Improving the Satellite
Communication.In: Proceedings CD of 2nd International ICST Conference on
Personal Satellite Services. Róma, Olaszország, 2010.02.04-02.05.,
1 – 14. oldal, 8560. publikáció
L Bacsardi, L Gyongyosi, S Imre: Solutions
for Redundancy-Free Error Correction in Quantum Channel.
In: Proceedings
CD of 1st International ICST Conference on Quantum Communication and Quantum
Networking. Vico Equense, Olaszország, 2009.10.26 – 10.30., Gent: 1 – 8. oldal,
8077. publikáció (ISBN: 978-963-9799-83-7)
L. Bacsárdi, M. Bérces,
S. Imre: Redundancy-Free Quantum Theory Based Error Correction Method in Long
Distance Aerial Communication.In: 59th International Astronautical
Congress, IAC Proceedings 2008. Glasgow, Nagy-Britannia, 2008.09.29 – 10.03.
1 – 7. oldal, IAC-08-B2.4.8. publikáció
Magyar nyelvű folyóiratcikkek
Bacsárdi László, Galambos Máté, Imre Sándor: Kvantumcsatorna a
műhold-Föld és a műhold-műhold kommunikációban.HÍRADÁSTECHNIKA LXV:(3 – 4.)
23 – 29. oldal (2010)
Ismeretterjesztő előadások
Bacsárdi László: Teleportálás fénysebességgel – kalandozások a
kvantuminformatikában
A jövő technikái, technikák a jövőből
rendezvénysorozat, Sopron, 2010. április 14.
Bacsárdi László,
Imre Sándor: A gyök NOT kapu rejtélye, azaz lehet, hogy nyugodtan alszik
holnap éjjel Mr. Moore?Puskás Tivadar Távközlési Technikum, 2010. március
29.
Bacsárdi László: Kvantuminformatika használata az
űrtávközlésben, avagy hazatelefonálhat-e E.T. a fénysebességnél
gyorsabban?Fényi Gyula Csillagászati Szabadegyetem, Sopron, 2007.
november 23.
Ismeretterjesztő írások
Bacsárdi László: Kalandozások a kvantumvilágban (2.
rész)
Impulzus (BME VIK HK lapja), XXXVII/7., (2010. május)
Bacsárdi László: Kalandozások a kvantumvilágban (1.
rész)
Impulzus (BME VIK HK lapja), XXXVII/6., (2010.
április)
Bacsárdi László: Fenyegető, titkos
kvantumvilág
THE tudománynépszerűsítő portál középiskolásoknak (2008.
július 24.)
Bacsárdi László: Merre tovább,
informatika?
THE tudománynépszerűsítő magazin középiskolásoknak (2008.
március)
Linkgyűjtemény
Kvantum-informatika és kommunikáció
választható tárgy honlapja
Kvantuminformatikával foglalkozó portálok (angol nyelven)
Quantiki
portál
Virtual Journal of Quantum
Information
The International Nanoscience
communicity
Kvantum cégek
id
Quantique
MagiQ Technologies
Quintessence Labs Solutions
Hivatkozások listája
[1] S. Imre, B. Ferenc: Quantum Computing and Communications: An Engineering
Approach, (Wiley, 2005)
[2] Michael A. Nielsen, IsaacL. Chuang: Quantum
Computation and Quantum Information (Cambridge University Press, 2000)
[3]
Charles H. Benett, Gilles Bassard: Quantum Chryptography: Public Key
Distribution and Coin Tossing, Internation Conference on Computers, Systems
& Signal Processing, Bangalore, India (1984. december 10 – 12.)
[4]
C. H. Bennett, G. Brassard, C. Crépeau, R.
Jozsa, A. Peres, W. K. Wooters: Teleporting an Unknown Quantum State via dual Classical and
Einstein-Podolsky-Rosen Channels, (Phys. Rev. Lett, 70. kötet, 13. szám, 1895. oldal,
1993. március)
[5] C. H. Bennett et al.: Lecture Notes In Computer Science 473, 253
(1991).
[6] Richard J. Hughes, Jane E. Nordholt, Derek Derkacs and Charles G.
Peterson: Practical free-space quantum key distribution over 10 km in daylight
and at night, (New Journal of Physics 4 (2002) 43.1 – 43.14)
[7] Tobias
S-Manderbach, et al.: Experimetal Demostration of Free-Space Decoy-State
Quantum Key Distribution over 144km, Phys. Rev. Lett. 98, 010504 (2007)
[8]
Josep Maria Predigues Armengol, et al.: Quantum Communications at ESA: Towards
a space experiment on the ISS, Acta Astronautica 63, 165 – 178 (2008)
[9] L.
Bacsardi: Satellite Communication Over Quantum Channel., Acta Astronautica
61:(1 – 6) 151 – 159. oldal, 2007
[10] Larry C. Andrews and Ronald L. Phillips:
Laser Beam Propagation through Random Media, (SPIE Press Book, 2005)
[11] C.
Bonato et al.: Polarization transformation induced on qubits in a
Space-to-Earth quantum communication link, Quantum Electronics and Laser
Science Conference (2007)
A képek és illusztrációk forrása: magyar és angol nyelvű Wikipedia,
szabadon használható illusztrációs képek, a Mobil Távközlési és Informatikai
Laboratórium hivatalos logója, valamint saját szerkesztésű
ábrák.
