 |
BMe Research Grant |

|
Pattantyús Ábrahám Géza Doctoral School of Mechanical Engineering Sciences
Department of Hydrodynamic Systems
Supervisor: Csaba Hős, Ph.D.
Optimal Control of Regional Waterworks
Introducing the research area
Nowadays, energy saving is gaining more and more importance in all industries. The water distribution system of a city is usually already given and can only be changed at extremely high cost. However, it can be operated in many different ways, resulting in different energy consumptions. The problem is then to find the pump schedule corresponding to the lowest energy consumption, which is important and challenging not only from the economical and environmental point of view but also scientifically as our optimization problem is large-scale, hybrid (integer and continuous variables are simultaneously present), heavily constrained, nonlinear and stochastic.
Brief introduction of the research place
The Dept. was founded in 1899 – then as Department of Hydraulic Machines – by Donát Bánki, who was its first professor. In 1930 Géza Ábrahám Pattantyús became the Head of Dept., whom we can recall as one of the most respected engineering pedagogues working in Hungarian higher education.
Nowadays 10 scientists and 9 PhD students are working at the Dept. on the following topics: blood flow in human arteries, water distribution systems, hydraulic and pneumatic systems, cavitation and acoustics, just to name the most important ones.
History and context of the research
One of the topics that have been dealt with at the Dept. for several decades is the hydraulics of pipe networks. The first area in which remarkable results were obtained was the steady-state behaviour of pipe networks, for which a specialized numerical technique was developed (pivoting of branch flow rates) for reducing the number of equations to be solved and hence speeding up the computation by one order of magnitude. Transient (water hammer) simulations were also studied extensively together with open-channel wastewater network computations. For all of these families of problems in-house code is available, which is continuously used both for research and industrial projects.
The forecast of water demand in a city is also an important problem to be solved. In [3], Bárdossy G. and Halász G. proposed a fuzzy logic-based procedure, which was found to be appropriate for short-term forecast (the next couple of days). At the present stage of the research, the overall daily consumption can be predicted with high accuracy and the possibilities of describing the demand during the day are studied.
My project deals with a novel area initiated by industrial needs: the pump scheduling problem, which focuses on computing the pump operation of the next (typically) 24 hour resulting in minimal energy consumptions. The know-how gained in the above described areas (steady-state and transient computations of pipe networks plus water demand forecast) are all needed and the topic is a natural continuation of the previous research. Up to 2009 the Dept. completed three such project with industrial partners.
Aim of the research
The aim of the project is to develop an algorithm capable of coping with waterwork systems of arbitrary size and complexity. By knowing the topology of the system (hydraulic properties of pumps, reservoirs, pipes etc.), the pump schedule with minimal energy consumption is to be determined, which also satisfies water demands. The term “pump schedule” simply means a set of rules describing when and which pump is to be switched on or off and their actual revolution numbers. If the tariff of the energy is constant during the day, then the schedules belonging to minimal energy and energy cost coincide. Moreover, the case of minimal energy is a special case of the more general problem of minimal energy cost.
Let us have a look at Figure 1., which contains all the important elements of our problem and consider the case when there is no reservoir. In this case water demands are covered by the pump directly; hence there is no room for optimization. However, in real systems, the reservoirs allow to cover the demands with several pump schedules as one can store the water and use later.
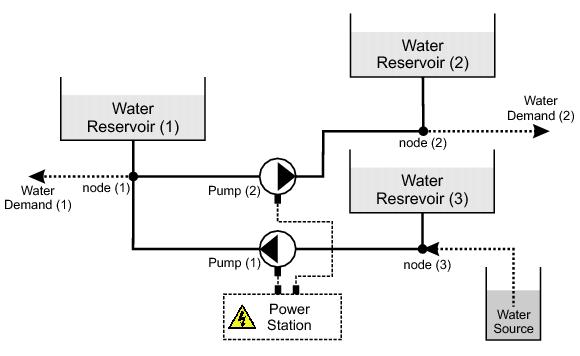
Figure 1: Test Network
The cut in the energy consumption originates from two sources: (a) the proper scheduling of reservoir filling and emptying and (b) by choosing the proper pumps to cover the demands. The latter one means that usually there are several pumps feeding the system and their specific energy consumption (the energy needed to feed unit volume of water into the system) are different. However, the actual revolution number, the instantaneous state of the network or the actual water levels of the reservoirs are all influencing the specific energy needed.
Moreover, the complex constraint system makes the problem even more complicated: the upper and lower levels of the reservoirs, the maximal allowable power of the pump groups, the pressure limits at the demand nodes or the capacity of the wells are all prescribed and to be fulfilled. It is also worth mentioning that the switching time of the pumps is also prescribed as too frequent switching decreases the expected lifetime of the pumps significantly. Thus, the scheduling takes space on a discrete 1-hour interval temporal grid that renders the optimization problem discrete.
Methods
As previously mentioned, the solution of the optimization problem is rather challenging. To gain an overview on the available techniques several benchmark problems with increasing complexity were defined, which were ran on the freely available solvers at the NEOS optimization server (http://www-neos.mcs.anl.gov/). These tests highlighted the fact that at the most realistic modelling level most of the solvers available at the web page (developed by the leading scientists of the world) failed to find even a feasible solution. A detailed summary of this study is given in [1].
There is a wide coverage of solutions for such optimization problems in literature, and these algorithms are mostly based on soft computing techniques. Our experiments also proved the suitability of soft computing techniques; hence our solver is a specialized genetic algorithm. The advantages of these techniques are their flexibility (capability of coping with heavily constrained nonlinear problems) and robustness. However, important drawbacks are the lack of well-developed mathematical background and the need for trial-and-error type tuning of parameters.
The solver used in our studies is a highly specialized one, the so-called Neutrally Coded Micro-Genetic Algorithm described in [2] is also available here. Its biggest advantage is that through neutrality the technique can be used to counteract “early convergence” phenomenon often encountered in the case of genetic algorithms, i.e. finding and “getting stuck to” a local minimum and thus missing the global optimum.
According to our experience, the problem of finding the first feasible solution (a pump schedule satisfying all the constraints) is of the same size as the actual optimization. The constraint handling of our algorithm is unique and given in [2], which was further developed in [1].
Results
As already mentioned, although the classic deterministic solvers tested were unable to solve the optimization problem, our solver was found to be appropriate. Moreover, our improved constraint handling algorithm was compared to the most wide-spread techniques in the literature in [2] and it was found that our algorithm ensures significantly faster convergence. A further improved version can be found in [1].
The present stage of the algorithm is continuously tested in industrial application: operation of the water distribution system of Sopron is based on the pump schedules computed by our algorithm. A typical computation takes 3-5 minutes on an average desktop PC and the resulting schedules are energetically better than those realized by the operators. There was no need for coupled hydraulic simulations here due to the well-defined operating points of the pumps.

Figure 2: Network of Sopron
An advanced version of the algorithm was developed for the Waterworks of Budapest, where a single typical computation takes 24 hours to complete. The reason for this large computational effort is the complexity of the system (47 pumps to be optimized, 12 reservoirs and a couple of hundreds of pipes) and the need of hydraulic system simulations.
The output of such a computation is the pump schedules for the next 24 hours and the predicted reservoir water level elevations as shown in Figure 3.
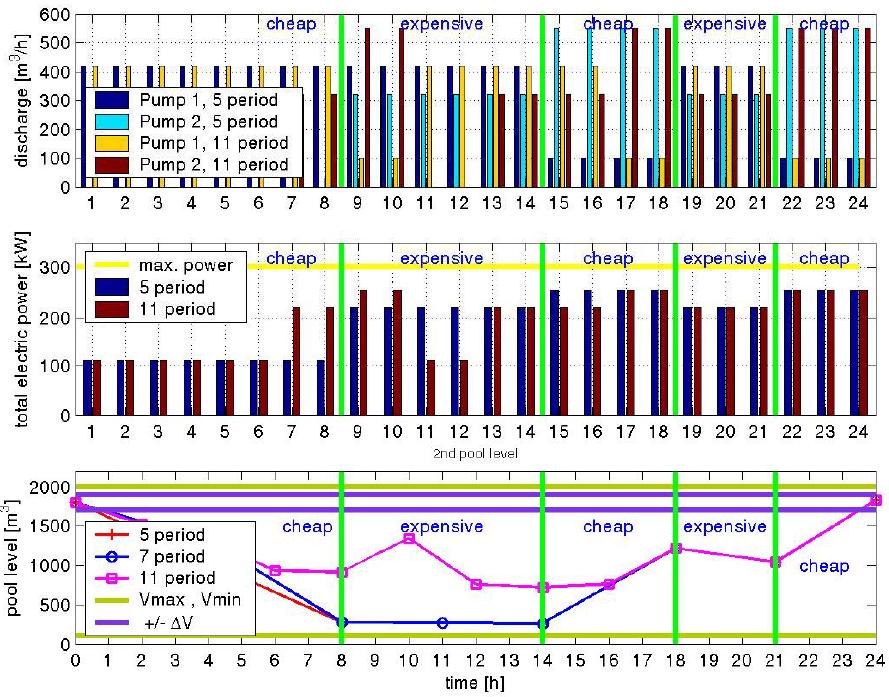
Figure 3: Results on the Test Network
Expected impact and further research
Based on our previous studies, two issues are important in regard to the industrial applications of the technique.
1) In the case of large industrial systems it is cumbersome to give a clear explanation of the results. On one hand, as the “real” optimal solution is unknown, it is hard to judge how “close” one gets to the optimal solution. On the other hand, due to the complexity of the system and the interaction between the elements it is almost impossible to explain the results merely by “engineering sense” – which would be extremely important when working with industrial partners. In many cases, even the operators with several decades of experience fail to give an energetically reasonable explanation of the proposed schedules. Thus an important headway of the future work is to study the system-pump interactions from an energetic point of view including the issues of the electric devices. Moreover, experience and know-how has to be gained on simple systems, on which the interaction between the system elements is easy to follow.
2) At its present state, the algorithm assumes accurate water demand prediction. However, whatever the demand prediction model is, it is loaded with more or less uncertainty and the question arises that if the optimal control is computed for a given demand which is later slightly disturbed, how close the “new” optimal schedule will be to the previously computed one. In extreme situations, the computed schedule might become infeasible in the case of the disturbed demands. Thus it is important to cope with the uncertain nature of the predicted water demands via stochastic techniques.
Publications, references, links
[1] Bene J., Hős Cs.: A Novel Constraint Handling Technique for Genetic Algorithm-Based Pump Schedule Optimization, 7TH INTERNATIONAL CONFERENCE ON MECHANICAL ENGINEERING (2010)
[2] Bene J. G., Selek I., Hős Cs.: Neutral Search Technique for Short-Term Pump Schedule Optimization, JOURNAL OF WATER RESOURCES PLANNING AND MANAGEMENT-ASCE 136:(1) pp. 133–137. (2010)
[3] Bárdossy Gergely, Halász Gábor, Winter János: Prognosis of urban water consumption using hybrid fuzzy algorithms, JOURNAL OF WATER SUPPLY RESEARCH AND TECHNOLOGY-AQUA 58:(3) pp. 203–211. Paper 448EQ (2009)
