Pattantyús Ábrahám Géza Gépészeti Tudományok Doktori Iskola

Hidrodinamikai Rendszerek Tanszék 

Témavezető: dr. Hős Csaba

Regionális ivóvízhálózatok költség- és energiahatékony üzemvitele

A kutatási téma néhány soros bemutatása

Napjainkban egyre nagyobb hangsúlyt kap az energiahatékonyság kérdése az ipar szinte minden területén. Bár egy város ivóvízellátó rendszere többnyire adott, és azon csak szélsőségesen magas költség árán lehet számottevően változtatni, a hálózat üzemeltetési módjában költség- és energiafelhasználás szempontjából jelentős különbségek lehetnek. A megoldandó probléma – a legkisebb energiafelhasználással megvalósítható üzemvitel megtalálása – nem csupán gazdasági, környezetvédelmi szempontból fontos, hanem tudományos szempontból is érdekes; ugyanis egy sokváltozós, kevert (egész és valós változók is jelen vannak), sok mellékfeltétellel terhelt, nemlineáris, sztochasztikus optimálási feladatot jelent.

A kutatóhely rövid bemutatása

A tanszéket Hidraulikai és Hidrogépek Tanszék néven első professzora, a határturbina elméleti kidolgozásáról ismertté vált Bánki Donát alapította 1899-ben. 1930-ban került a tanszék élére Pattantyús Ábrahám Géza,  akire a hazai műszaki felsőoktatás legnevesebb mérnökpedagógusaként emlékezhetünk.

A tanszéken jelenleg 10 főállású oktató-kutató és 9 PhD hallgató dolgozik a következő kutatási témákon (a teljesség igénye nélkül): emberi véráramlás (artériás, vénás hálózat, kisvérkör, agyi anaurizmák), ivóvízhálózatok (üzemvitel-optimalizáció, hálózatszimuláció, lengésvédelem), hidraulikus és pneumatikus hajtások, kavitáció, akusztika (élhang, üreghang vizsgálata).

A kutatás történetének, tágabb kontextusának bemutatása

A Hidrodinamikai Rendszerek Tanszéken hosszú ideje foglalkoznak a csőhálózatok hidraulikájával. Első kimagasló eredményeiket a csőhálózatok stacionárius hidraulikai szimulációjában érték el a vízhálózatot leíró egyenletrendszer méretének radikális csökkentésével, amire az ún. bázisáram-kiválasztás adott lehetőséget. Napjainkra az ivóvízhálózatok időfüggő szimulációjára, illetve lengésvédelmi számításokra is képessé váltunk, akár nyílt felszínű ágakat tartalmazó hálózat esetében is.

Egy város vízfogyasztásának előrejelzése szintén fontos probléma. A tanszéken Bárdossy Gergely és Dr. Halász Gábor fuzzy-logika alkalmazásával próbálja megoldani a feladatot [3]. A munkák jelenlegi szakaszában a napi összes vízfogyasztást jó közelítéssel képesek becsülni az előrejelzett hőmérséklet- és csapadékadatok alapján, a napon belüli fogyasztás alakulásának becsléséhez azonban még további kutatások szükségesek. 

A fent leírt témakörök mindegyikét a Tanszék ipari szakértői tevékenységei motiválták. Az elmúlt években az ország három nagyobb városa vízműhálózatának energiaminimum melletti optimális üzemét vizsgáltuk. Két ilyen projekten jelenleg is dolgozunk.

Saját kutatási témám az előbb felsorolt eredmények mindegyikére épít, hiszen a vízműhálózat napi üzemvitelének optimalizálásához szükségünk van a rendszer hidraulikai viselkedésének és a becsült vízfogyasztások ismeretére is.

A kutatás célja, a megválaszolandó kérdések

A kutatás célja egy olyan algoritmus fejlesztése, amellyel a fogyasztói igényeket a lehető legkisebb költség- illetve energiaráfordítás árán kielégítő üzemvitel határozható meg a tetszőleges méretű és bonyolultságú ivóvízhálózat topológiája (szivattyúk, víztározó medencék, csövek, csőszerelvények hidraulikai jellemzői és kapcsolódási pontjai), valamint a lakossági és ipari vízfogyasztások ismeretében. Üzemvitel alatt tipikusan a következő 24 órára meghatározott, ún. szivattyúmenetrendet értjük, amely pontosan meghatározza, hogy a nap során mikor kell ki- és bekapcsolni, illetve milyen fordulatszámon kell működtetni a szivattyúkat. Amennyiben a villamos tarifarendszer (a szivattyúk számára villanyáramot biztosító szolgáltató tarifája) a nap során nem változik, úgy a költség- és energiaoptimum egybeesik. Megállapítható továbbá, hogy az energiaoptimalizálás a költségoptimalizálás egy speciális esete. 

A feladat megértéséhez vegyük az 1. ábrát, mely egy valós vízműhálózat összes, a feladat szempontjából lényeges elemét tartalmazza, és kiindulásként tételezzük fel, hogy a hálózat nem tartalmaz víztározó medencéket. Ekkor minden időpontban közvetlenül a szivattyúk által kell ellátni a fogyasztókat, pontosan az igényeiknek megfelelő mennyiséggel. Ebben az esetben az optimalizáció értelmét veszti, hiszen csupán egyféle menetrend fedezi az igényeket. A valós hálózatokban azonban mindig vannak medencék – ezek jelentik a hálózat tárolási kapacitását. Ezek felhasználásával már többféle szivattyúmenetrenddel is kielégíthetők a fogyasztói igények, hiszen a felesleges víz bennük tárolható, illetve onnan később kinyerhető. 

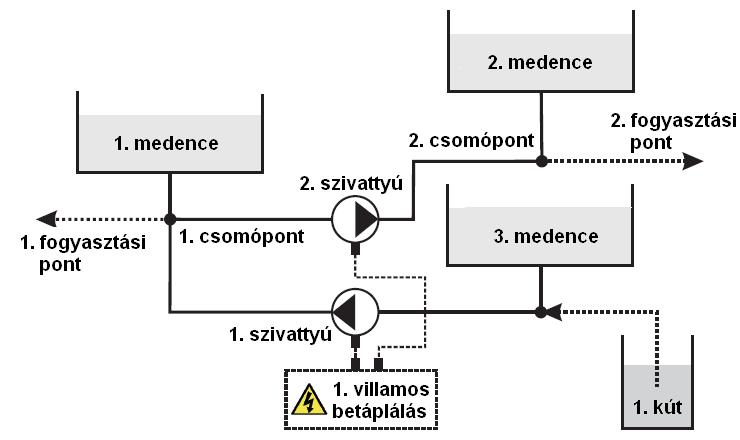
1. ábra: Mintahálózat 

Költségmegtakarítás alapvetően két módon érhető el: a medencék töltésének, illetve ürítésének megfelelő ütemezésével, valamint a víz útjának helyes megválasztásával, mely utóbbi alatt azt értjük, hogy a víz mely szivattyúk munkájának eredményeképpen jut el az elvételi helyekhez. Ez utóbbi azért befolyásolja a költségeket, mert az egyes szivattyúknak más-más fajlagos energiafelhasználásuk van (adott mennyiségű vizet más és más villamosenergia-felvétel mellett képesek szállítani), ráadásul ezen jellemzőjüket befolyásolja az aktuális fordulatszám, sőt, visszahat rájuk a hálózat állapota (például a medencék aktuális szintjei) is. 

A megoldandó optimalizációs problémát számos mellékfeltétel is bonyolítja, pl. a medencék minimum és maximum szintjei, a gépházak felvett teljesítményére előírt maximumok, a fogyasztási pontokban előírt nyomáshatárok, kutak kitermelési korlátai. Mivel a szivattyúk túl gyakori kapcsolása hidraulikai és karbantartási okokból nem megengedett, ezért a szivattyúk üzemállapotát csak óránként változtathatjuk, vagyis az optimalizációs feladat időben diszkrét. 

Módszerek 

A megoldandó (kevert változós, időben diszkrét, nemlineáris, mellékfeltételekkel erősen terhelt) optimalizálási feladat meglehetősen bonyolult. A szóba jöhető megoldó algoritmusok felmérése céljából az optimálási feladathoz különböző modellezési szinteken és méreteken mintafeladatokat készítettem, melyeket ezután futtattam a http://www-neos.mcs.anl.gov/ weboldalon megtalálható, kutatási célra szabadon hozzáférhető optimalizáló szolverekkel. A tesztek arra a következtetésre vezettek, hogy a probléma a legmagasabb modellezési szinten – amely természetesen a legjobban közelíti a valóságot, és így a való életben a legjobban használható – nem oldható meg a honlapon megtalálható, a világ élvonalába tartozó optimalizáló eljárásokkal sem. Az algoritmusok részletes összehasonlítása az [1] irodalomban található.

A szakirodalomban azonban számos olyan, általában a soft computing, az ún. lágy számítási módszerek közé sorolható algoritmus ismeretes, melyek a hasonlóan nehéz optimalizálási problémákat is képesek megoldani. Így saját kutatásaim során is az ebbe a családba tartozó, ún. genetikus algoritmusokkal foglalkoztam. A genetikus algoritmusok előnye, hogy kevéssé érzékenyek a feladatok bonyolultságára, tehát képesek megoldani mellékfeltételekkel terhelt, nemlineáris problémákat is. Hátrányuk, hogy matematikai hátterük kidolgozatlan, és a működést befolyásoló számos paramétert sokszor próbálgatással kell beállítani.

Az általunk használt megoldó az ún. mikro-genetikus algoritmusok családjába tartozik. Az általunk vizsgált feladatra azonban nem volt alkalmas egy megszokott, szakkönyvekből kivehető algoritmus. Az általam és szerzőtársaim által kifejlesztett új algoritmus, az ún. NGA (Neutral Genetic Algorithm) részletes ismertetése a [2] irodalomban található, amely itt is elérhető. Legnagyobb előnye, hogy képes elkerülni a genetikus algoritmusokra egyébként rendkívül jellemző korai konvergenciát, mely azonban általában csak egy lokális szélsőértékhely megtalálását jelenti a globális optimum helyett.

Tapasztalataink szerint az optimalizálás során a mellékfeltételek teljesítése legalább olyan szintű kihívást jelent, mint magának a célfüggvénynek a minimalizálása. Az algoritmus mellékfeltétel-kezelése már [2] megjelenésekor is teljesen egyedi volt, később kutatásaim során ezt továbbfejlesztettem; ezt az algoritmust [1] mutatja be.

Eddigi eredmények 

Mint fentebb említettem, az adott optimalizációs problémát az általam kipróbált, hagyományos, determinisztikus módszerekkel nem sikerült megoldani. Ezzel szemben saját fejlesztésű algoritmusunk képes erre. Saját algoritmusunk mellékfeltétel-kezelési módszerét [2]-ben összevetettük a legelterjedtebb, genetikus algoritmusok esetén alkalmazott módszerekkel, melynek eredményeképpen megállapítható, hogy saját mellékfeltétel-kezelésünk gyorsabb konvergenciát biztosított. Ennek továbbfejlesztett változatát mutatja be [1], amely még hatékonyabban keresi meg a mellékfeltételeket teljesítő megoldásokat. 

A jelenlegi algoritmus ipari körülmények között is több alkalommal ki lett próbálva. Először a Sopron és Környéke Víz-és Csatornamű Zrt. kezdte tesztelni, és ma már kijelenthető, hogy a soproni hálózaton (ld. 2. ábra) az algoritmus egy átlagos asztali PC-n kb. 3-5 perc alatt képes legalább olyan jó, megvalósítható menetrendeket készíteni, mintha kézi irányítással működött volna a vízmű. Ebben az  esetben még nem volt szükség komplex hidraulikai szimulációra, mivel a szivattyúk munkapontjai a nagy geodetikus szintkülönbségeknek köszönhetően nagyjából állandóak. 

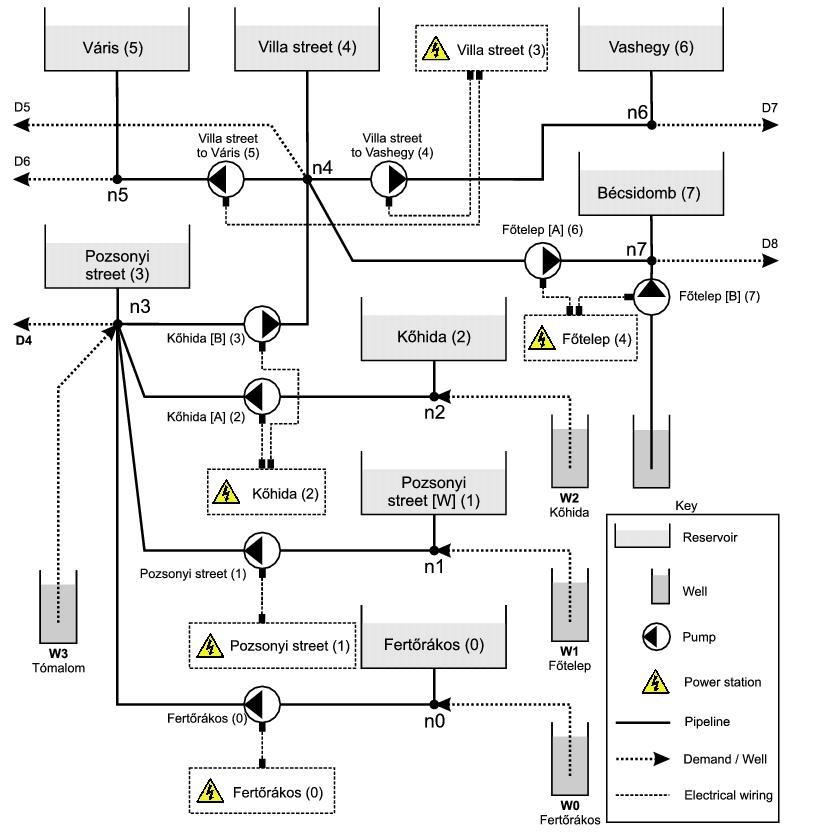
2.ábra: A soproni hálózat 

Az algoritmus legfejlettebb változata a Fővárosi Vízművek Zrt. alapzónájának üzemvitel-optimalizációjára képes, a futásidő itt még kb. 24 óra. A hosszú futásidő oka elsősorban a hálózat hatalmas mérete (47 db optimalizálandó szivattyú, 12 medence, több száz csővezeték még az egyszerűsített modellekben is) és a komplex hidraulikai szimuláció szükségessége. 

Az optimalizáció eredményeként az összes esetben rendelkezésre állnak a következő 24 órában beállítandó szivattyú-menetrendek, valamint a fogyasztások alapján előrejelzett medenceszint-változások. Ezekre mutat egy egyszerű példát az 1. ábrán bemutatott mintahálózat esetén a 3. ábra. 

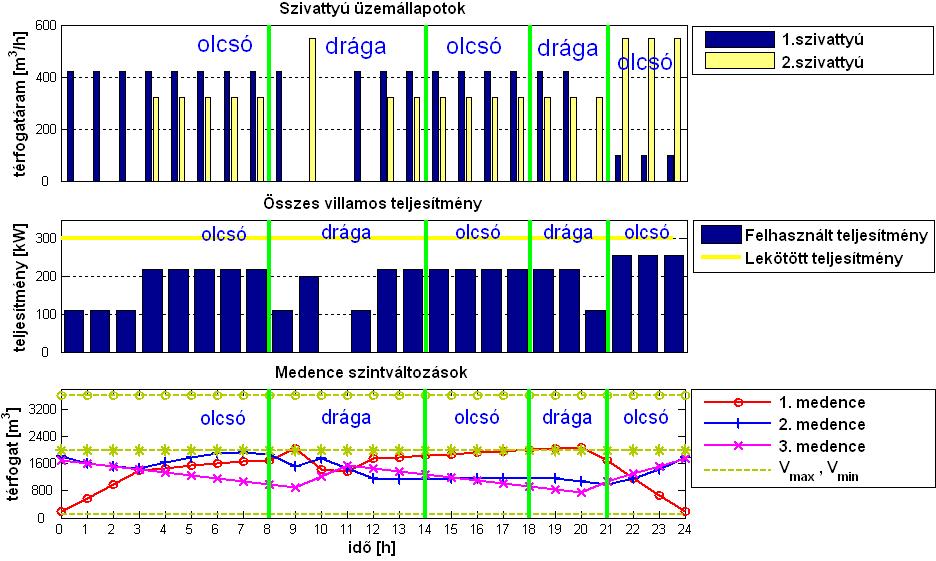
3.ábra: A mintahálózatra kapott eredmények 

Várható impakt, további kutatás 

Az előzőekben bemutatott eredmények gyakorlati használhatósága szempontjából két dolgot emelek ki. 

Összetettebb ipari eseteknél tapasztaltuk, hogy nagyméretű, komplex ivóvízhálózatra kapott optimálás eredményei olykor nehezen értelmezhetők. Egyrészt nem állapítható meg – mivel a feladatot megoldó determinisztikus eljárás nincs a birtokunkban – , hogy milyen közel jutott az optimálás által meghatározott célfüggvényérték a valódi, globális optimumhoz. Másrészt a hálózati elemek egymásra hatása miatt sokszor „józan ésszel” sem magyarázható, hogy egy adott szivattyú miért pont az eredményül kapott időpontban kapcsoljon be. Az algoritmussal kapott eredmények legtöbbször a nagy üzemirányítási tapasztalattal rendelkező vízműves kollégák által is megmagyarázhatatlanok; még a költséghatékonyság szempontból egyértelműen kedvezőbb esetekben is. Éppen ezért kutatásaim egyik jövőbeli célja a szivattyúk energetikai viszonyainak alapos vizsgálata áramlástani szempontból és az alkalmazott villamos hajtás tekintetében, majd az itt szerzett ismeretek ellenőrzése egyszerű, könnyen érthető mintahálózatokon, amely eredmények alapján a nagyobb hálózatok működésére lehet következtetni.

Mint ahogy az előzőekben leírtam, az általam készített algoritmus képes valós vízműhálózatok optimális üzemvitelének meghatározására – determinisztikusnak feltételezett vízfogyasztások esetén. Ezen vízfogyasztások az irányítási feladat bemenő paraméterei, melyeket statisztikákból vagy fogyasztás-előrejelzésekből nyerünk. A feladat további nehézségét azonban éppen ezen vízfogyasztások sztochasztikus jellege adja. Mivel a valós  fogyasztások eltérnek ettől, ezért hiába kapunk a bemenő adatok tekintetében optimális üzemvitelt, a fogyasztások bizonytalansága miatt a valóságban ez egyáltalán nem biztos, hogy optimális, sőt, az sem biztos, hogy megvalósítható.  A valós rendszeren végzett vizsgálataink is azt támasztják alá, hogy az optimális üzemvitel birtokában előre jelzett változók (pl. medenceszintek) el fognak térni a valóságostól. A fentiek miatt a kutatás egy további lehetséges iránya a fogyasztások sztochasztikus változóként való kezelése. 

Saját publikációk, hivatkozások

[1]  Bene J., Hős Cs.: A Novel Constraint Handling Technique for Genetic Algorithm-Based Pump Schedule Optimization, 7TH INTERNATIONAL CONFERENCE ON MECHANICAL ENGINEERING (2010)

[2] Bene J. G., Selek I., Hős Cs.: Neutral Search Technique for Short-Term Pump Schedule Optimization. JOURNAL OF WATER RESOURCES PLANNING AND MANAGEMENT-ASCE 136:(1) 133–137. oldal (2010) 

[3] Bárdossy Gergely, Halász Gábor, Winter János: Prognosis of urban water consumption using hybrid fuzzy algorithms, JOURNAL OF WATER SUPPLY RESEARCH AND TECHNOLOGY-AQUA 58:(3) 203–211. oldal 448EQ cikk (2009)