 |
BMe Research Grant |

|
Pál Csonka Doctoral School
Department of Mechanics, Materials and Structures
Supervisor: Prof. Gábor Domokos
The morphology of pebbles
Introducing the research area

What shape is a pebble? - the aim of my PhD research is to answer this fundamental question.
The great diversity and beauty of pebble shapes have always posed a puzzle for scientists. The basic idea of the research is that the concept of static equilibria offers a natural classification system to encode pebble shapes. In my PhD research I investigate the mathematical background of this new classification system and apply the system to describe the morphology and the abrasion process of pebbles.
Brief introduction of the research place
The Department of Mechanics, Materials and Structures is engaged in a big variety of problems in the field of mechanics and structural design. Research topics are not only related to steel, timber, reinforced concrete, composite, membrane, masonry and adobe structures but there are also ongoing researches in the areas of earthquake engineering and stability of structures. Our research area includes a wide range of mechanics and applied mathematics, in addition to morphology and abrasion processes of pebbles, members of our department also investigate shape dynamics of asteroids, the morphology of turtles and stability problems of colliding bodies.
History and context of the research
Since Aristotle [6], many illustrious scientists have been interested in the geometry of pebbles [7][8]. Pebble shapes also attract considerable attention nowadays [9][10][11] because investigation of natural shapes formed by abrasion processes (e.g. landforms, asteroids or pebbles) helps understand abrasion processes themselves. Pebble shapes carry important information on the history of sediment transport and deposition [12][13], thus an appropriate shape classification helps differentiate facies.

Despite the extensive literature on the topic, there is little agreement on the best classification method for pebble shape analysis [17][18]. Geologists have developed a big variety of standardized shape indices and shape classification systems for rough estimation of pebble morphology [13][14][15][16]. These classical methods rely on length measurements, the simplest and most widespread classification system set up by Zingg [16] who proposed approximating pebbles with a three-axial ellipsoid and classified shapes based on the axis ratios. While these classical systems have undoubtedly proved to be useful tools, their application inevitably requires tedious and ambiguous measurements, and the classification involves the introduction of arbitrarily chosen constants.
The research goal, open questions
The aim of my research is to propose a new and completely different classification system for pebble morphology. As the new system does not rely on length measurements, it does not suffer from ambiguities that can be found in classical methods. Our method is readily applicable in field work as well. The new classification system encodes shapes based on the number and type of static equilibria and the relationships between equilibrium points.
The basis of the code is the number of stable and unstable equilibrium points. Based on these two natural numbers every homogeneous, convex body can be classified unambiguously [19], and the result is called the primary equilibrium class of the body. For example, the cube belongs to class {6,8} because there is a stable point on each of the 6 faces and each of the 8 vertices is an unstable point. The Gömböc [20], invented by Gábor Domokos and Péter Várkonyi belongs to class {1,1} (mono-monostatic body).
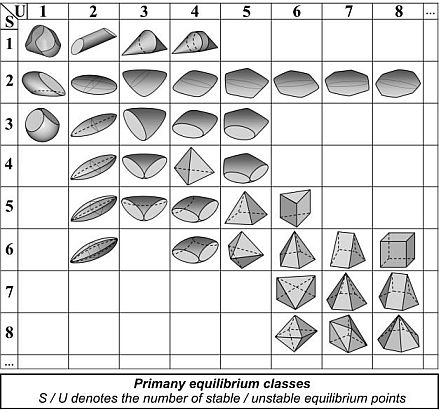
Morphology can be more accurately described if we take into account which equilibrium points are neighbors on the surface. These adjacency relationships define a graph on the pebble's surface, which is called the secondary equilibrium class of the body.
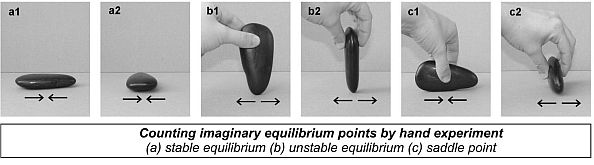
The above described classification system can be further refined with the concept of imaginary equilibrium points. Through the "magnifying glass" we can observe numerous microscopic equilibrium points on the pebble's surface: these are the real equilibria of the pebble. However, outside observers cannot discriminate microscopic real equilibria by eye because they occur in highly localized groups (flocks) [3][4] on the surface, thus human experimenter perceives these flocks only as imaginary equilibria.
My PhD research includes the mathematical study of the new classification system based on primary, secondary, imaginary and real equilibria, as well as the practical application of the new system to examine pebble morphology. The latter includes sampling and classifying pebbles in geologically significant places and also, statistical evaluation of the results.
The other main goal of my research is to understand and model abrasion processes of pebbles, especially considering the above described new classification system. This involves fieldwork, laboratory experiments and investigating analytical and numerical abrasion models. Our equilibrium system uses only natural numbers, thus every shape can be described by a code, and change of the code can be followed up with the appropriate mathematical and technical tools during the abrasion process. The aim of the research is to understand the changes in the morphology through the changes of code, and to assign different code sequences to different abrasion processes.
Methodology
Imaginary equilibrium points of a pebble can be counted in simple and fast hand experiments. Typical 3D bodies may have three types of equilibrium points: stable equilibria, unstable equilibria and saddle points; their number will be denoted by S, U and H, respectively. The Poincare-Hopf Theorem [21] establishes the relationship S+U-H=2 for bodies with spherical topology, hence we only have to count stable and unstable equilibrium points, the number of saddle points can be computed. Based on hand experiment, {S,U} is the primary class corresponding to imaginary equilibria of the pebble.
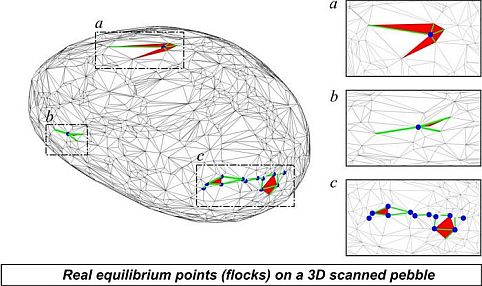
Identifying real equilibria on a pebble is a more complex task, however, the information contained is also more detailed. Microscopic real equilibria can be detected by modern 3D scanning technology, the high-accuracy (0.1 mm) scanning was performed at the Department of Manufacturing Sciences and Technology, using a 3D laser scanner mounted on a CNC machinery. The result of the scanning process is a many-faceted, triangulated polyhedral surface, on which equilibrium points can be identified by an appropriate computer algorithm.
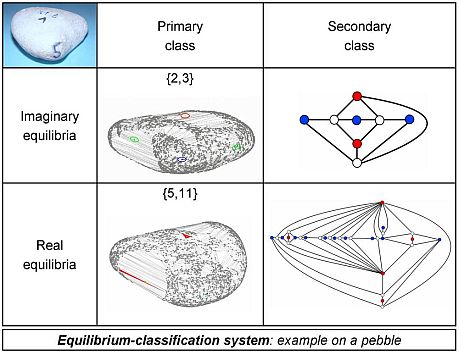
Secondary class is determined by the topology of the Morse–Smale-complex [22], which is built up by the heteroclinic orbits between equilibrium points. The topology of this Morse–Smale complex can be illustrated by a planar graph: equilibrium points are the vertices of the graph and there is an edge between two equilibrium points if they are neighbors on the pebble's surface. The graph corresponding to real equilibria can be simplified with an algorithm [22] until microscopic real equilibrium points disappear and only the macroscopic, imaginary equilibria remain that can be observed by hand experiments. Geometrically, simplification of the Morse–Smale complex corresponds to "smoothing" of the polyhedral surface.
Results
Determining the number of imaginary equilibrium points can be done in seconds by very simple and fast hand experiments. This promises to be of great advantage in geological fieldwork. Despite the simplicity of this code, these two natural numbers describe the geometry of the pebble adequately since there is a strong relationship between the Zingg-classes and primary (imaginary) equilibrium classes. Based on data of 1000 measured well-worn pebbles we found that the simplified version of equilibrium classification contains all the information contained in the Zingg system, with up to 10-20% inaccuracy [1][2]. However, the new system is more sophisticated: it may help to identify shape attributes unexplored so far as it is able to store information on special geometries, e.g. on crystal shapes [2]. Primary class is also closely connected to roundness: as an example we mention that the classical Zingg system cannot make a difference between tetrahedral and cubic shapes, while equilibrium classes {4,4} and {6,8} give clear descriptions of these shapes.

Using the above described 3D scanning technology, we showed that microscopic real equilibrium points on pebbles are accumulated in highly localized groups (flocks), the latter can be perceived as imaginary equilibrium points in hand experiments. Except for spherical pebbles, the scales of real and imaginary equilibria (micro- and macro-equilibria) are well separated [3], thus imaginary equilibria (flocks) can be reliably counted in a hand experiment, i.e. our new classification system is practically applicable.
The number of real equilibria inside a flock is closely related to the local geometry of the surface. Let us given a smooth surface with an equilibrium point P; in [4] we showed that the number of equilibrium points emerging on the fine polyhedral discretization of the surface depends on the distance of Pto the center of gravity and the two principal curvatures of the surface at P.
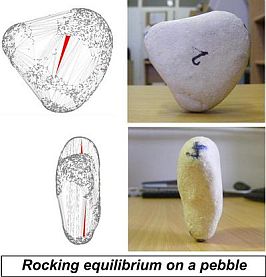
The concept of real and imaginary equilibria provides a framework to explain an interesting phenomenon: the amazing and counter-intuitive equilibrium position of rocking stones. These large stones are so sensitively balanced that despite their large mass, even a small force applied causes them to rock. Because of their strange attitude, rocking stones were connected to plenty of beliefs in the past, e.g. they were associated with witchcraft. Rock-balancing artists produce similar but smaller scale artworks. We introduced the concept of rocking equilibrium to explain this phenomenon [3]: rocking equilibrium is a stable real equilibrium belonging to an unstable imaginary equilibrium. The concept of rocking equilibrium clearly explains why we feel that equilibrium position of rocking stones is counter-intuitive: outside observer does not perceives the microscopic stable equilibrium point, only the macroscopic unstable (imaginary) equilibrium.
As earlier researches have proved that every primary equilibrium class is nonempty [19], it is natural to ask whether or not it also holds for secondary equilibrium classes. Recently we have shown that it does, i.e. we can show a corresponding smooth, homogeneous, convex body [5] for every combinatorially possible graph.
Further research
In the course of further research we plan to perform meaningful field measurements in which we collect pebble samples from locations of geological interest. A thoughtful selection of geological locations allows us to examine different depositional environments to follow up and distinguish different abrasion processes. Besides this, we plan to perform laboratory experiments and we work on numerical and analytical models of abrasion processes. Our final goal is to understand and model different abrasion processes of different depositional environments, using the new classification system to encode shapes. In June 2012, collaborating with The University of Newcastle, I collected pebble samples under the supervision of geologist Prof. Stephen Fityus along the Williams River in New-South Wales, Australia. Sampling focused on the basalt particles originating from the Barrington Tops basalt plateau, allowing us to follow the abrasion process of basalt pebbles in the river.
Publications, references, links
Publications:
[1] G. Domokos, A. Sipos, T. Szabó, P. Várkonyi (2010), Pebbles, Shapes, and Equilibria, Mathematical Geosciences, Vol 42, 29–47
[2] T. Szabó, G. Domokos (2010), A new classification system for pebble and crystal shapes based on static equilibrium points, Central European Geology, Vol 53/1, 1–19
[3] G. Domokos, A. Sipos, T. Szabó (2012), The mechanics of rocking stones: equilibria on separated scales, Mathematical Geosciences, Vol 44/1, 71-89
[4] G. Domokos, Zs. Lángi, T. Szabó (2011), On the equilibria of finely discretized curves and surfaces, Monatshefte für Mathematik, DOI: 10.1007/s00605-011-0361-x
[5] G. Domokos, Zs. Lángi, T. Szabó, The genealogy of convex solids, in preparation, Manuscript PDF on arXiv
Links:
BME Department of Mechanics, Materials and Structures
Rocking stones:
Youtube: Bill Dan rock-balancing artist
References:
[6] Aristotle, in Minor Works, Mechanical Problems, Question 15, translated by W. S. Hett (Harvard University, Cambridge, MA, 2000)
[7] Lord Rayleigh (1942), Pebbles, natural and artificial, Proc. Roy. Soc. London A, Vol 182, 107-118
[8] F.J. Bloore (1977), The shape of pebbles, Math Geol, Vol 9, 113-122
[9] W. Ashcroft (1990), Beach pebbles explained, Nature, Vol 346, 227
[10] M. Lorang, P.D. Komar (1990), Pebble Shape, Nature, Vol 347, 433-434
[11] T. Yazawa (1990), More pebbles, Nature, Vol 348, 398
[12] D.J. Graham, N.G. Midgley (2000), Graphical representation of particle shape using triangular diagrams: an Excel spreadsheat method, Earth Surf Proc Land, Vol 25, 1473-1477
[13] E. Sneed, R.L. Folk (1958), Pebbles in the lower Colorado River, Texas, a study in particle morphogenesis, J Geol, Vol 66, 114-150
[14] W.C. Krumbein (1941), Measurement and geologic significance of shape and roundness of sedimentary particles, J Sed Petr, Vol 11, 64-72
[15] C.K. Wentworth (1922), The shapes of beach pebbles, US Geological Survey Professional Paper, Vol 131-C, 75-83
[16] T. Zingg (1935), Beitrag zur Schotteranalyse, Schweizer Miner, Petrog. Mitt., Vol 15, 39-140
[17] W. Illenberger (1991), Pebble shape (and size!), J Sed Res, Vol 61, 756
[18] S.J. Bott, K. Pye (2008), Particle shape: a review and new methods of characterization and classification, Sedimentology, Vol 55, 31-63
[19] P. Várkonyi, G. Domokos (2006), Static equilibria of rigid bodies: dice, pebbles and the Poincaré-Hopf Theorem, J Nonlinear Sci, Vol 16, 255-281
[20] P. Várkonyi, G. Domokos (2006), Mono-monostatic bodies: the answer to Arnold’s question, Math Intell, Vol 28, 34-38
[21] V.I. Arnold (1998), Ordinary differential equations, 10th printing, MIT Press, Cambridge
[22] H. Edelsbrunner, J. Harer, A. Zomorodian (2003), Hierarchical Morse-Smale complexes for piecewise linear 2-manifolds, Discrete Comput Geom, Vol 30, 87-107
